基于自适应无迹卡尔曼的目标跟踪算法研究

卢颖鹏，陈 曦，杜忠华，侯 杰

（南京理工大学机械工程学院，江苏南京 210094）

目标跟踪算法是装甲车主动防护系统的核心算法之一，目标跟踪精度和收敛速度对最终的拦截概率影响很大[1-3]。选择合适的滤波算法可以得到相对精确的来袭目标运动信息，进而提升目标拦截概率。

文献[4]在引入径向速度信息的基础上采用比例对称采样策略(Scale symmetry sampling)优化UKF(Unscented Kalman Filtering)算法(以下简称SUKFR)[4]，得出SUKFR 算法相较于其他算法滤波的收敛速度更快且精度更高，但该算法没有考虑异常干扰的影响。文献[5]提出了一种基于自适应无迹卡尔曼滤波(Adaptive Unscented Kalman Filtering,AUKF)的状态估计算法，优化了常规UKF 算法抗干扰性能差的问题[5]，但其滤波收敛速度还可以进一步提高。

为增强装甲车主动防护系统性能，提高目标拦截概率，该文引入噪声自适应系数对SUKFR 算法进行优化(以下简称ASUKFR)，通过Matlab 仿真对比UKFR、SUKFR和ASUKFR的滤波效果，得出ASUKFR算法滤波效果更好，且在该算法下目标拦截概率最优。

1 算法描述

常规UKF 算法利用无迹（Unscented Transform,UT）变换处理非线性系统均值和协方差的传递问题，在保留高阶项的基础上，有效避免了非线性系统的线性化，提高了系统高斯密度的传递精度[6]。ASUKF 算法对常规UKF 算法容错性能差和采样非局部性的问题进行优化，具体步骤如下：

步骤1：计算Sigma 采样点集，并对获得的Sigma点集进行一步预测：

式（1）中共有2n+1 个采样点；X为状态变量；n为状态的维数；上标i为第i个采样点；为状态变量均值；P为方差矩阵；λ为缩放比例系数。

然而，在标准UKF 算法中，当维数n增大时，Sigma 点与均值点的距离也会变大，进而出现采样的“非局部效应”，且量测方程函数非线性强弱会直接影响算法的整体滤波精度。为解决算法的“非局部效应”并且保证协方差矩阵的半正定性，考虑对此前得到的Sigma 点集进行比例采样修正[7]，以避免采样的“非局部效应”，其公式如下：

式（2）中，a为比例修正参数，取值范围为[0,1]，X(i)(k+1|k)为Sigma 点集的一步预测，f为系统状态量的非线性变换。

步骤3：对一步预测值使用UT 变换，得到新的Sigma 点集k+1|k)。

步骤4：将步骤3 得到的新Sigma 点集代入观测方程，计算得到新的观测量Z(i)(k+1|k)。

步骤5：通过对上一步计算的观测预测值进行加权，得到系统预测均值和协方差，并引入噪声自适应系数进行优化[8]。

步骤1 中引入比例修正系数，虽然消除了采样的“非局部效应”，但是在实际应用中，UKF 滤波算法对滤波的初始值比较敏感，这可能导致滤波发散[9]。因此，该文在比例修正的基础上引入噪声自适应系数对原算法进行优化，噪声自适应系数不仅可以估计和校正不确定系统模型噪声和噪声统计参数，还可以使用量测值对预测值进行修正[10-11]。所以对传统的预测协方差进行如下更新：

式（3）中，ω为采样点权值，下标c表示协方差；αk为噪声自适应系数，并且0 ＜αk≤1。

采样点权值计算如下所示：

式（4）中，参数α决定了采样点的分布状态，取值范围为[0.000 1,1]；参数κ为冗余值，一般取0；参数β为权系数；n为状态向量的维数。

选择适当的自适应系数，不仅可以平衡状态方程估计量和观测信息的权重，还可以控制异常干扰对系统估计结果的影响[12]。αk的取值如下：

式（5）中，预测残差mk=Z(i)(k+1|k)-(k+1|k)。

步骤6：计算Kalman 增益矩阵K(k+1|k)。

由上述算法步骤可知，ASUKF 算法通过比例修正系数消除常规UKF 算法采样的“非局部效应”，再引入噪声自适应系数来调节k+1|k)在估计过程中的权重，从而提升算法的滤波性能。

2 目标跟踪

2.1 来袭目标假设

主动防护系统的拦截面是以装甲车辆中心为圆心、半径为8 m 的半球面。由于雷达探测距离只有200 m，并且来袭目标飞行速度较快，系统对雷达测量轨迹数据的滤波时间须小于300 ms，因此，雷达需要保证较快的探测速率，从而提供较多的来袭目标运动数据，确保目标的跟踪精度，雷达每1 ms 向系统传输一次来袭目标的位置和速度信息。

为简化模型，对主动防护系统目标跟踪作出如下两点状态假设[13]：

1）由于来袭目标飞行速度远大于装甲车的行驶速度，所以假设来袭目标从被探测到被拦截的过程中，装甲车辆处于近似静止的状态。

2）该系统采用的是超近程主动防护策略，在雷达探测到来袭目标时，其已经处于飞行的最后阶段，运动轨迹不会发生较大波动，因此，可以近似看作匀速直线运动。

2.2 目标运动方程

该文采用CV（Constant Velocity）模型来描述来袭目标的三维运动状态。由于雷达采样有时间间隔，为了方便控制系统处理，对雷达采样数据进行离散化处理，其状态方程表达式如下：

2.3 目标量测方程

雷达量测采用球坐标系，目标量测数据包括径向距离r、俯仰角α、方位角β和径向速度vr。该文假设来袭目标的位置和速度信息噪声都为独立的高斯白噪声，因此，量测方程为：

3 仿真试验

3.1 仿真参数设置

假设来袭目标距离装甲车200 m，俯仰角为20°，方位角为35°，速度为425 m/s；初始协方差矩阵P=1 000×eye(6)（eye(6)为6 行6 列的单位矩阵）；过程噪声调节参数σ2=1；雷达采样周期为1 ms；雷达采样总时间为0.4 s，无迹变换参数α=0.01，β=2，κ=0，状态向量维数n=6，比例修正系数a=0.1。量测噪声协方差矩阵R=

3.2 算法滤波效果对比

用Matlab 软件对ASUKFR、SUKFR 以 及UKFR算法进行50 次Monte Carlo 仿真，对比三种算法的滤波性能。由图1 可知，ASUKFR 和SUKFR 算法明显比UKFR 算法滤波效果更好，滤波轨迹更加贴近目标的真实轨迹。

图1 目标滤波轨迹对比

为了更直观地对比三种算法的优劣，采用均方根误差作为性能评价准则对滤波算法性能进行评价[14]，其公式如下：

式中，RMSEk为均方根误差，μ为RMSE 均值，N表示蒙特卡罗仿真次数，Xi(k)和分别为第i次仿真中时刻k的目标状态真实值和估计值；L为单次仿真采样次数。

由表1可知，ASUKFR和SUKFR的滤波精度都远远优于UKFR，并且ASUKFR 在保留SUKFR速度精度的基础上，径向距离滤波误差降低至原来的50%左右。图2 中，在径向距离滤波均方差方面，ASUKFR算法收敛速度最快，SUKFR 算法次之，UKFR 算法最慢，ASUKFR 算法在150 ms 左右已经达到稳态，而SUKFR算法和UKFR 算法分别在340 ms 和350 ms 附近达到稳态；而图3 中，ASUKFR 和SUKFR 算法的速度滤波均方差收敛速度相当，明显优于UKFR 算法。因此，ASUKFR 滤波稳定性更好且收敛速度更快。

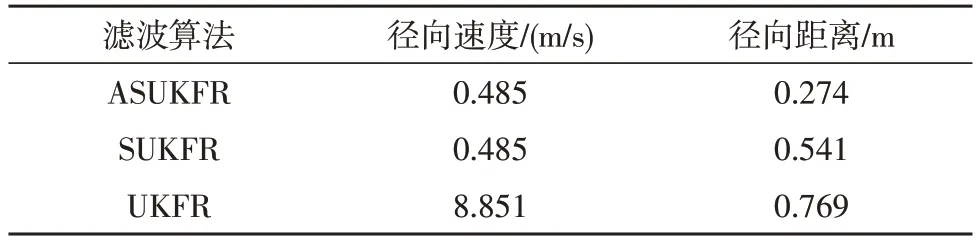
表1 50次蒙特卡罗仿真RMSE均值

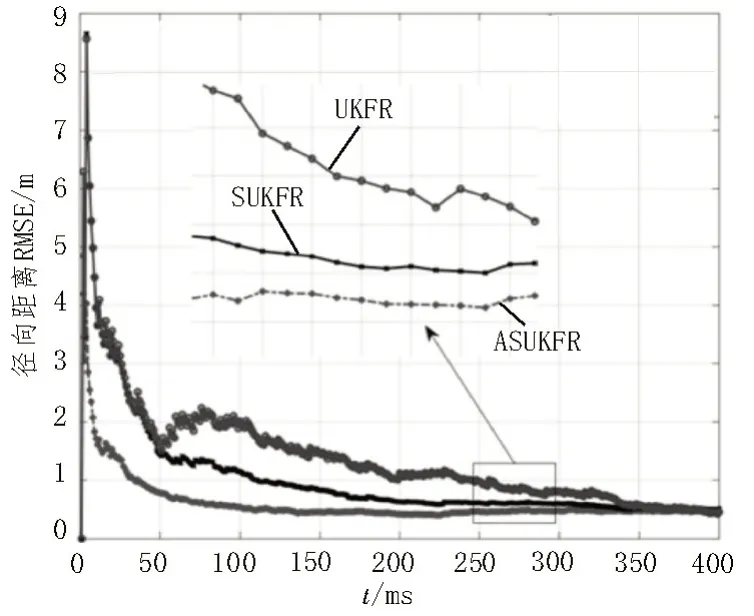
图2 径向距离滤波均方差

图3 径向速度滤波均方差

3.3 拦截概率仿真

以蒙特卡罗方法为理论基础，采用Matlab 软件对系统的拦截概率进行仿真。该理论利用不确定变量的随机值，通过大量的仿真实验得到结果[15]。

拦截概率计算过程：首先，根据目标运动状态方程和雷达量测方程生成来袭目标运动参数；其次，在生成的标准目标运动参数的基础上，叠加经过蒙特卡罗方法处理后的雷达量测和目标运动状态误差[16]；然后，对生成的量测轨迹进行滤波处理和拦截坐标点解算；最终，来袭目标拦截成功取决于系统解算的拦截坐标点和实际目标拦截点的间距，若间距不大于0.8 m（0.8 m 内飞网拦截效果最佳）则判定拦截成功，否则判定拦截失败。

由图4 可知，使用UKFR 算法后的系统拦截概率略优于直接使用量测数据的拦截概率；使用SUKFR算法后使得系统拦截概率相比UKFR 算法提升了约15%；ASUKFR 算法在SUKFR 算法的基础上引入自适应系数后，系统拦截概率提升至90%以上，仿真验证了该系统采用ASUKFR 算法能够更好地减小雷达量测噪声，增加主动防护系统的拦截概率，从而有效地保护装甲车辆。

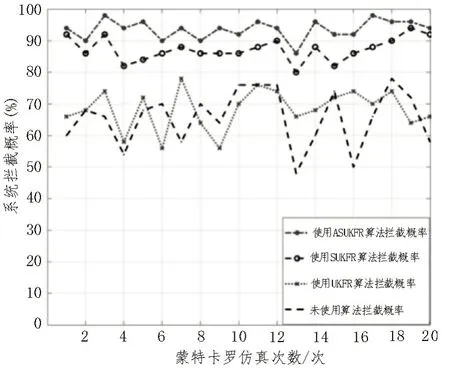
图4 不同滤波算法的系统拦截概率

4 结论

该文对装甲车主动防护目标跟踪技术进行研究，在SUKFR 的基础上引入噪声自适应系数来调节异常扰动，从而对系统估计结果进行修正。通过蒙特卡罗方法[17-18]验证了噪声自适应系数的引入能够有效改善目标跟踪的精度与稳定性，提高最终的系统拦截概率，得出ASUKFR 算法作为主动防护系统的目标跟踪算法，可以进一步提升装甲车战场作战和生存能力。