连杆轴承润滑空化过程动态仿真与抑制
尹晓青,杨康博,徐菁菁,李渴忻,杜祥宁,黄钰期
(1. 潍柴动力股份有限公司 内燃机可靠性国家重点实验室,山东 潍坊 261061;2. 浙江大学 动力机械及车辆工程研究所,浙江 杭州 310027)
空化现象是由于液体中的局部低压使液体汽化或者溶解于液体中的气体释放,从而引起的微气泡爆发性生长.当气泡塌陷后,产生的冲击波会造成固体表面的腐蚀,并伴有严重的噪声和振动.对于连杆轴承中的润滑油膜,空化现象引起的气蚀会导致轴瓦表面材料脱落从而在轴瓦表面形成不规则蚀坑,成为轴承失效的主要因素之一.近年来柴油机趋于更高功率密度,使得轴承的工作条件进一步恶化,当转速和爆压提升后,连杆空蚀的现象更为显著,成为掣肘高强度柴油机功率密度进一步提升的瓶颈.因此,探明连杆轴承润滑过程中出现的空蚀机理,对预测连杆轴承可靠性和寿命,提出可行抑制方案具有十分重要的现实意义.
由于柴油机轴系结构复杂、空间紧凑,在运行过程中很难直观测量轴承内部的油膜运动特性与相关参数.计算流体力学(CFD)仿真方法在研究轴承润滑的过程中,可以在获得油膜内的压力、流速和温度分布等各种细节数据的同时,对油膜的空化情况做出评估[1-7],是目前研究摩擦润滑空化问题的有效手段.早在2005 年,Guo 等[6]就使用CFD 的方法对动压轴承的静态性能进行了研究.王康等[7]则进一步探究了网格划分对使用CFD 方法研究空化现象的影响.张楚等[8]提出了采用两相流理论求解轴承润滑过程的CFD 模型,提高了求解计算的效率;彭立强等[9]也采用CFD 方法研究了滑动轴承油膜内单气泡的破裂扩散过程;季斌等[10]采用VOF 模型对轴承油膜中的气泡裂变及运动轨迹进行了仿真研究.此外,还有不少研究[11-13]探讨采用不同空化模型对CFD 计算结果的影响.这些研究在分析空化现象机理的同时,也提高了使用CFD 方法研究轴承润滑过程时的准确性和效率.
尽管对于轴承运动过程中的空化现象已经有了较多的研究,但如何改善轴承润滑性能,提高轴瓦寿命与可靠性依旧是一个有待解决的问题.刘黄亮[14]通过建立滑动轴承的CFD 三维模型,分析了表面织构的分布位置和几何参数对滑动轴承性能的影响.李新新等[15]发现提高润滑油的黏度以及供油的压强可以减弱空化现象.这些研究为如何提升轴承的润滑性能、减弱空化提出了有效的策略.但由于以上研究大多基于稳态分析,忽略了轴颈与轴瓦之间的相对间隙变化,因此,所获得的空化区域大体上固定不变,无法体现空化发生与溃灭的过程,更无法建立空化与空蚀之间的关联影响规律.而且发动机连杆轴承润滑的供油方式极具特点,需要经过主轴承旋转过程,从主轴的横油道进入斜油道,再到达连杆轴承区域.这一过程导致连杆轴承的供油压力并非稳定不变,而存在与转速周期相同的波动,这也可能是造成柴油机连杆轴承相比于主轴承更易空蚀的根本原因.而以往研究大多孤立地考虑轴承润滑本身,未考虑供油方式可能造成油压波动,因而对空化的预测可能存在较大误差;所提出的优化策略针对不同机型的柴油机时也难以获得推广应用.
笔者在前期动态仿真分析的基础上[16],探究因主轴承供油所导致的油压波动对连杆轴承润滑空化的影响,分析润滑油膜中的空化分数和压力变化,根据研究结果提出基于结构优化的空化抑制策略,并结合仿真对优化策略做进一步优化,为改善轴承运动过程中的空化现象,提高轴承性能提供参考.
1 研究对象
以潍柴某重型柴油机的连杆轴承作为研究对象,提取轴承之间的润滑油膜建立相应的几何模型.图1为该柴油机的供油结构.发现润滑油从各个支路经轴瓦进入主轴承后,随主轴颈的旋转运动进入横油道,再经斜油道进入连杆轴承的轴颈处.由于主轴承油膜在旋转时也存在较大压力波动,进入连杆轴承的润滑油必定也处于波动状态.

图1 某款柴油机轴承供油结构Fig.1 Bearing oil supply structure of a diesel engine
为了细致考虑润滑过程中的油膜动态空化与压力变化,从柴油机轴系中提取连杆大头轴承润滑油膜,作为主要研究对象.图2 展示连杆轴承所设定的相对运动方式,综合考虑了轴承运动中所包含的转动和平动,其网格形式、动网格设置方法等与前期研究一致[16].
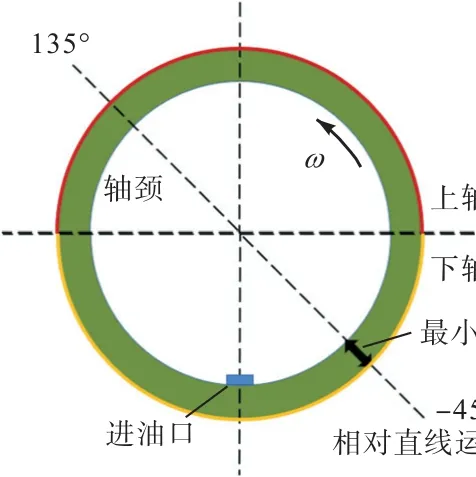
图2 连杆轴承相对运动方向示意Fig.2 Relative motion direction of connecting rod bearing
2 仿真模型建立
2.1 控制方程与空化模型
研究使用ANSYS Fluent 19.2 开展数值模拟,其质量和动量守恒方程的微分形式定义为
式中:ρ 为流体密度;v 为速度矢量;p 为压力; gρ为重力;F 为外部体积力以及依赖于模型和用户自定义的源项;为应力张量.在求解过程中选用3DDouble Precision-Pressure Based 求解器与Mixture 多相流模型,压力-速度耦合则采用SIMPLEC 算法.
对于考虑传热的可压缩流动过程,其能量方程定义为
式中:k 为有效导热系数;T 为温度;h 为比焓;Sh为热源项(如内部热源);E 为常数.
在前期研究[16]中对比了Singhal 模型、Schnerr and Sauer 模型和Zwart-Gerber-Belamri 模型3 种空化不同模型在计算润滑油膜空化时的准确度,最终选取Singhal 模型作为所采用的空化模型,并开展数值模拟计算.
2.2 边界条件
根据柴油机连杆轴承的实际运行工况与相关经验数据,仿真计算的边界条件是:位于连杆轴颈的进油口(润滑油从主轴承进入横油道,再经曲轴斜油道进入连杆大头轴承时的进口)设置为压力入口,而且进油的方向与进油口表面有一定的角度(与斜油道倾斜角度一致).对于恒定压力入口条件,入口压力为565 kPa;对于波动压力入口条件,入口压力为随时间变化的正弦函数.其中波动周期为轴承旋转周期,压力的波动范围则根据主轴承内油膜压力沿轴承表面的压力峰值进行多点平均后确定.将连杆轴承的轴瓦表面设置为旋转面以还原轴颈和轴瓦之间的相对旋转运动,轴瓦面的温度取140 ℃;轴承间隙两侧端面设为压力出口,表压为0 Pa;润滑油入口压力与温度根据给定参数进行设定,具体数据如表1 所示.

表1 油膜主要参数及数值Tab.1 Main parameters and values of oil film
其中润滑油表面张力设定为0.071 7 N/m,液态密度和液态黏度分别由10~150 ℃之间的18 个温度点的数据,通过分段插值方法确定,每两个温度点之间的变化关系按线性插值方法计算;气态比热容则由式(5)确定.
2.3 网格无关性分析与仿真验证
使用Hypermesh 14.0 软件对油膜进行结构网格划分.为实现边界运动和网格变形,避免负体积的出现,对进油口做了一些近似处理,由此在轴颈面上生成四边形结构网格,然后在径向进行拉伸,生成整体结构网格,计算域和网格形式示意如图3a 所示.通过稳态分析,对比不同尺寸网格所获得的油膜的周向气相体积分数以及压力分布可以发现,随着网格数目的增多,仿真得到的油膜压力与气相体积分数变化不大见图3b.结合计算资源综合考虑,最后选用网格数为9.6×105的划分方法进行模拟计算.

图3 计算域、网格形式说明及无关性分析Fig.3 Computing domain,grid form description and independence analysis
在前期研究[13,17]中通过与文献[18—19]数据的对比,证明了所采用的仿真方法可准确模拟轴承润滑过程中的周向压力与温度分布.为进一步验证仿真,采用上述方法对某实机轴承润滑过程开展仿真,对比该轴承在疲劳试验运行后发生空蚀的位置如图4 所示,发现仿真获得的剧烈空化区与轴承实际发生空蚀损伤的形状和位置均较为一致,表明该方法在预测空蚀方面也具有较高的可靠性.

图4 仿真空化区域与试验损伤区形状对比Fig.4 Shape comparison between simulated cavitation area and test damage area
3 计算结果及讨论
3.1 入口油压波动对润滑空化的影响
由图1 可知,润滑油从各支路首先到达主轴承,对主轴承进行润滑后,从位于主轴承轴颈两侧的出口进入横油道,汇流后经曲轴上的斜油道到达连杆轴承的轴颈,再对连杆轴承进行润滑.因此,主轴承油膜的内部压力直接关联连杆轴承的润滑油入口压力.而在以往研究与工程经验中,均发现主轴承油膜沿周向的压力存在明显差异,经主轴承进入横油道的润滑油压力也不可能是稳定不变的,这可能对连杆轴承的空化情况产生重要影响.
由此,采用动网格模拟轴承润滑过程中的平动(轴承间隙变化)与转动(轴承旋转),对不同入口条件的轴承润滑过程进行仿真计算.为还原轴颈和轴瓦之间的相对运动,通过编辑用户自定义函数(UDF)文件,将油膜模型中的轴颈面设置为沿-45°与135°方向(图2 中的虚线)的直线运动.其中,轴颈的移动速度为0.72 mm/s,最小油膜厚度在1~500µm 范围内变化,如图5a 所示.图中红色实线为连杆大头轴承的轴心轨迹,蓝色线为曲柄梢(连杆轴颈)的轴心轨迹.当两者的轴心轨迹距离最远时,表明轴颈在轴承内出现了最大的偏置,轴承间隙最小,因而油膜厚度也最小.从图5a 来看,最小油膜厚度出现在图中红色虚线框所示的位置,这一过程对应了柴油机在不同冲程时,连杆大头轴承旋转的同时在径向负荷作用下贴近再远离轴颈的过程.因而将该部分运动近似为黑色实线箭头所示的运动,作为径向相对运动的依据.入口压力则设置为正弦波动函数,波动振幅从0到565 kPa,对应转速为1 800 r/min,负荷为4 kN 时油膜的峰值压力为1.13 MPa(主轴承轴颈的出油口为横油道,当油道一端对应峰值压力时,另一端压力为0,因而取横油道两端压力的平均值作为连杆入口压力峰值).

图5 最小油膜厚度与入口压力波动随时间变化示意Fig.5 Schematic diagram of minimum oil film thickness and inlet pressure fluctuation with time
由于最小油膜厚度的出现是因为轴颈的径向移动,假设最小油膜厚度用d 表示,则在油膜间隙逐渐缩小的过程中,有
在油膜间隙逐渐增大的过程中,有
式中:t 为时间,在每个过程的起始时,时间初始化为0.
根据这一设置开展仿真,得到了不同压力条件下油膜的相关数据见图6,其中进油口为斜油道与连杆轴承的接触口(图3a).对比稳定入口和波动入口下的压力峰值的变化规律可以发现,当最小油膜厚度较大(大于110µm)时,油膜的压力峰值主要受到入口压力的影响,特别是在波动入口条件下,油膜的压力峰值随时间的变化规律与入口压力的波动规律一致.当最小油膜厚度较小(小于110µm)时,此时的油膜压力峰值主要受到最小油膜厚度的影响.两种入口条件下油膜的压力峰值均在这一阶段显著上升,但相比波动入口,恒定入口条件下的压力峰值上升更为显著.这可能是因为进油口处与压力峰值处有一定的距离(图2),随着轴承旋转,波动的入口条件对最小间隙处的高压反而起到了一定的消解作用.
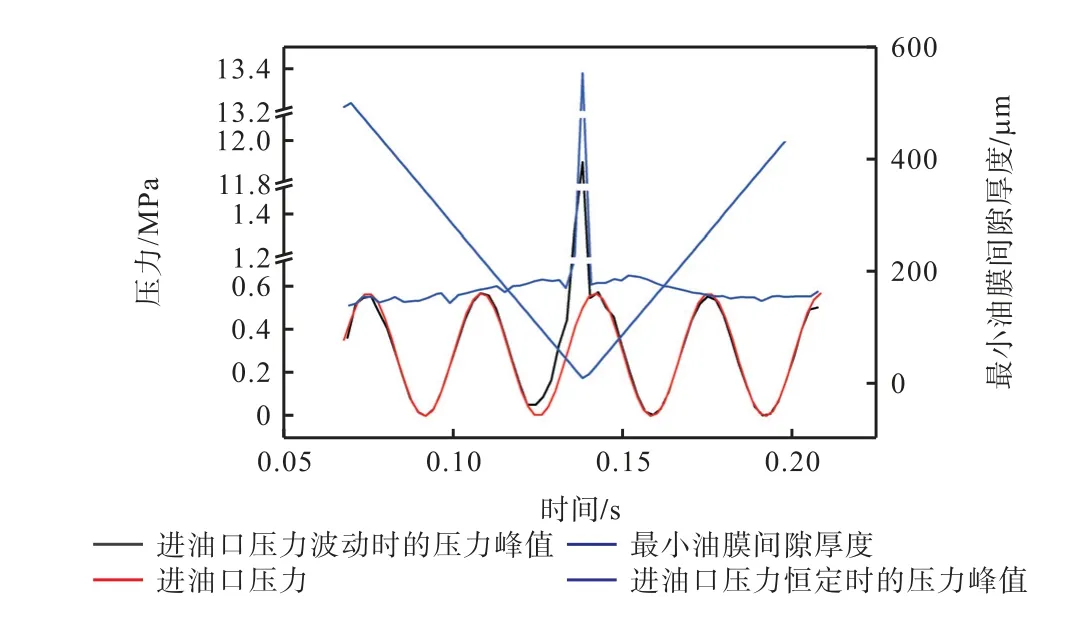
图6 不同入口条件下的油膜压力峰值随时间变化Fig.6 Variation of oil film pressure peak value with time under different inlet conditions
虽然波动入口与恒定入口压力在油膜周向压力上有较大差距,但从图7 气相分数峰值来看,却发现两种工况的峰值空化程度非常接近.在波动入口条件下,气相体积分数的峰值变化趋势与入口压力的变化相近,在最小油膜厚度开始增大的过程,也就是空化现象最严重时,气相体积分数的峰值在两种入口条件下达到的最大值基本一致(均为0.94).表明空化现象的位置和严重程度主要受到轴承运动的影响,而非油压入口条件的影响.
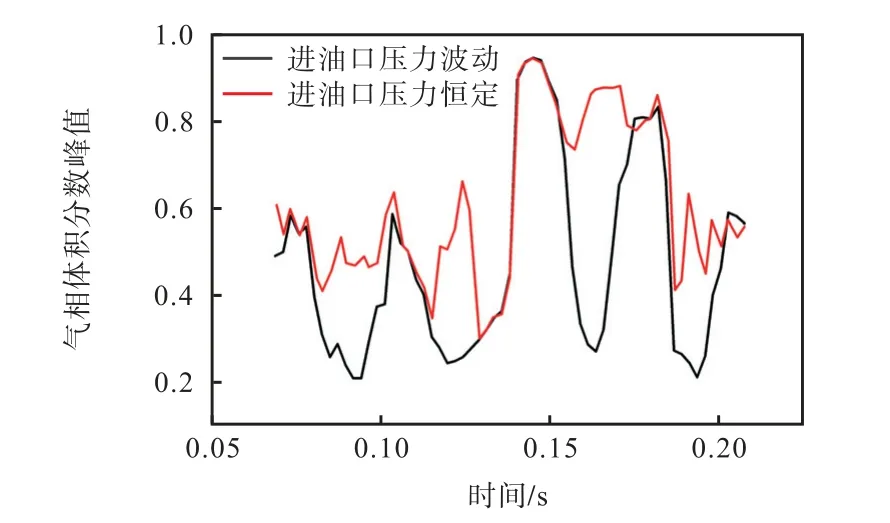
图7 不同入口条件下油膜的气相体积分数峰值随时间变化Fig.7 Changes of peak volume fraction of the oil film vapor phase under different inlet conditions with time
但是,相比于恒定入口条件,在波动条件下,当最小油膜厚度增大时,空化峰值会急速下降,表明此时出现显著的空化溃灭现象.总体来看,入口油压波动会导致空化状态的迅速变化,气相体积分数出现多个陡升陡降的过程,这种快速的空化-溃灭更易引发空蚀.这一现象也解释了重型柴油机中,为何相对于主轴承,连杆轴承的空蚀程度远远要更为恶劣.
3.2 轴瓦开槽对空化过程的影响
轴瓦开槽被认为是缓解连杆轴承空蚀的一种有效策略,但开槽方式如槽宽、槽深和槽长等却并无定论.因此,进一步采用数值仿真方法比较轴瓦开槽对空化的影响.前期研究发现,虽然入口油压波动会影响空化的发生和溃灭频率,但并不会影响空化分数,也就是空化发生的剧烈程度.所以在对比开槽和槽深的影响时,选用稳态计算方法.图8 列出不同的开槽方式,而总的槽宽和槽深一致.此外,还对比了同时在上、下瓦开槽与仅在下瓦开槽的影响.
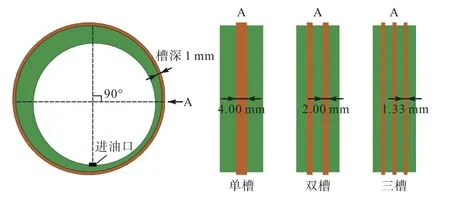
图8 轴瓦开槽的位置以及油槽宽度示意Fig.8 Position of the bearing grooving and the width of the sump
图9 和图10 分别为不同开槽数的油膜气相体积分数和油膜压力分布.这里重点显示了气相体积分数较高(大于0.5)和压力较高(大于10 MPa)的区域.可以看出,气相体积分数较高的区域位于最小油膜厚度的下游位置,而压力较高的区域主要位于最小油膜厚度的上游位置;开槽可以明显改变空化区的形态,使得空化区从连续的舌型分裂成面积较小的梯形.当油槽的数目连续增多时,通过进一步减少连续的空化区范围,从而限定了空化气泡的大小和大面积同步溃灭的可能,也增加抑制空化现象的效果.

图9 不同开槽数的油膜气相体积分数分布Fig.9 Volume fraction distribution of oil film vapor phase with different numbers of grooves

图10 不同开槽数的油膜压力分布Fig.10 Oil film pressure distribution with different numbers of grooves
图11 为不同开槽情况下的周向油膜气相体积分数以及周向油膜压力的对比.其中,气相体积分数和压力均沿油膜的径向和轴向求平均.开槽可以显著降低气相体积分数的大小以及油膜空化的范围.对于槽的总宽一定的条件下,槽数的增多能进一步地提高缓解空化现象的效果,但是提升的程度却逐渐减弱.对于油膜的压力分布而言,相比于无槽模型,开槽可以有效地降低油膜压力.其中,单槽和三槽模型降低油膜压力的效果更加显著,这可能是因为轴承沿轴向方向的中线位置是承压最显著的地方,压力波动最为剧烈,此处开槽可以对峰值压力进行一定程度的控制.综合来看,采用单槽或者三槽是更为合理的优化方式.
3.3 不同槽深对空化现象的影响
综合加工可行性与强度需求,在单槽的基础上考虑了4 种不同的油槽深度,分别为0.5、1.0、1.5 和2.0 mm.通过仿真计算得到了不同槽深的油膜压力与油膜气相体积分数如图12 和图13 所示.增加槽深能够使空化范围减小,改变空化范围的形状,进一步缓解空化.

图12 不同槽深的油膜气相体积分数分布Fig.12 Volume fraction distribution of oil film vapor phase at different groove depths

图13 不同槽深的油膜压力分布Fig.13 Oil film pressure distribution at different groove depths
图14 为不同槽深的油膜气相体积分数和油膜压力沿周向位置的分布.开槽的深度会影响油槽缓解空化现象的效果.随开槽深度的增加,空化范围和程度都有一定的减少,但总体提升幅度有限.从无槽到开槽1.0 mm 所带来的缓解空化现象的效果要明显高于从开槽1.0 mm 到开槽2.0 mm 提升的效果.这可能是因为槽的厚度(1.0 mm)已经远大于油膜最小间隙处的厚度(1.0µm).结合图14b 可知,0.5~1.0 mm的槽深已经能够明显改善轴承内部最小油膜厚度处的压力峰值和空化分数,达到抑制空蚀的效果.
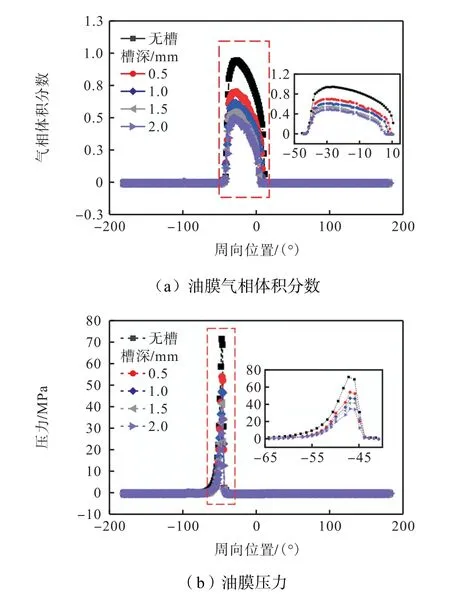
图14 不同槽深的油膜气相体积分数和油膜压力沿周向位置分布Fig.14 Volume fraction of the oil film vapor phase and oil film pressure at different groove depths distributed along the circumferential position
3.4 不同槽形对空化现象的影响
最后,通过不同槽形对空化现象的影响效果进行探究.在上瓦和下瓦全槽模型的基础上,设计了半槽模型.其中半槽模型中油槽的范围为-180°~0°(参考图2 中的角度分布).图15 和图16 分别示出槽深为1.0 mm 的不同槽形模型的油膜气相体积分数和油膜压力分布.相对于全槽模型而言,半槽模型更能缓解油膜的空化现象.特别是在改变空化区域形状方面,半槽模型中的空化区域远离油槽,空化范围也显著减小.这可能是因为在半槽模型中,处于最小油膜厚度下游的润滑油从油槽中流出的时候,一部分从油槽末端流出,另一部分则从油槽的两侧流出,形成了沿轴向的流动,使得半槽模型中油槽两侧的空化区域范围被进一步“挤压”,有效缓解了空化现象.图17 显示半槽模型中润滑油在最小油膜厚度下游的流动情况,也进一步证实了半槽模型中空化区域较小的原因.
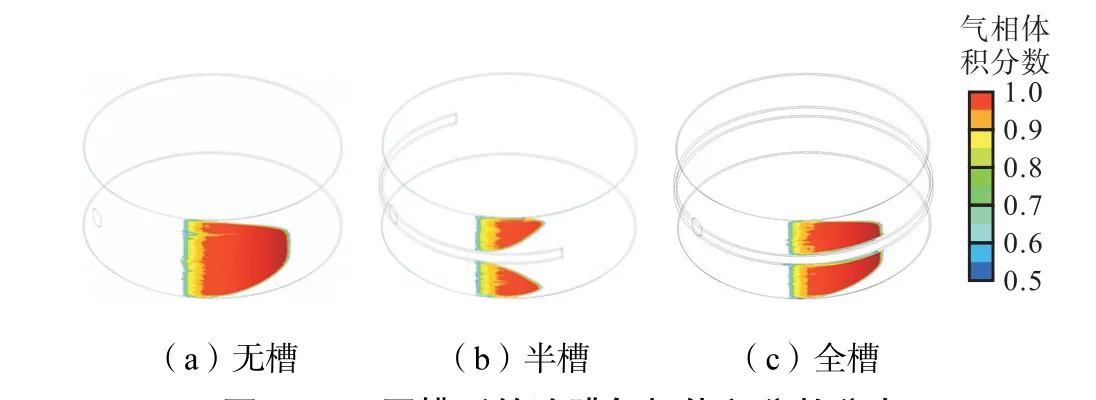
图15 不同槽形的油膜气相体积分数分布Fig.15 Volume fraction distribution of oil film vapor phase of different grooves
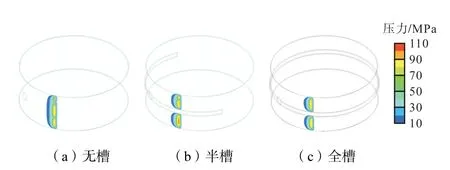
图16 不同槽形的油膜压力分布Fig.16 Oil film pressure distribution of different grooves

图17 半槽模型中油膜流线Fig.17 Oil film streamlining in a half-groove model
图18 为不同槽形的油膜气相体积分数和油膜压力沿周向位置的分布.从图18a 可以得到,无槽、半槽和全槽3 种模型的气相体积分数最大值分别为0.94、0.61 和0.39.相比于无槽模型,半槽模型将气相体积分数的最大值降低了58.51%.从图18b 可以看出,半槽和全槽模型对轴承内部最小油膜厚度处的压力改善效果较为接近.因此,结合轴瓦整体结构可靠性需求,选择适当槽深的半圈单槽即可有效抑制油膜的空化现象.

图18 不同槽形的油膜气相体积分数和油膜压力沿周向位置分布Fig.18 Volume fraction of the oil film vapor phase and oil film pressure of the different grooves distributed along the circumferential position
4 结 论
以潍柴某型号的柴油发动机连杆轴承润滑油膜为研究对象,通过动网格动态仿真计算得到了油膜压力及气相体积分数随轴承运动的变化情况,探讨了入口压力波动对连杆轴承润滑空化可能的影响,并对比了不同的油槽设计对抑制空化的影响,得到的结论主要如下:
(1) 由于柴油机供油特性,连杆轴承中的润滑油入口条件必然存在波动;而波动入口条件下,虽然油膜的气相体积分数在峰值数据上与恒定入口工况几乎一致,峰值压力还有所降低,但油膜内气相体积分数的变化却受入口压力波动的影响发生剧烈变化,对应着频繁的空化溃灭,可导致更为严重的空蚀破坏;这一发现解释了柴油机连杆大头轴承相较于主轴承更易发生空蚀的客观现象.
(2) 轴瓦开槽确实能有效减缓空化,其中增加槽数和槽深均能够提升抑制效果,但随着油槽数目和油槽深度的进一步增加,提升的程度逐渐减少.
(3) 槽型对油膜空化现象的影响较大,在油槽深度和数目一致的情况下,半槽模型可以引发油膜内发生轴向流动,显著改变油膜空化区域的形状,相比全槽模型具有更好的抑制效果,可将气相体积分数最大值从未开槽时的0.94 降至0.39.
总体来看,综合轴瓦的厚度与强度需求,选择适当槽深的半环单槽或三槽即可有效地抑制轴承运动过程中油膜的空化现象;这一结论不仅适用于所研究的重型柴油机,也可为其他机型的优化提供参考.

