A three-dimensional feature extraction-based method for coal cleatcharacterization using X-ray μCT and its application to a Bowen Basin coal specimen

Yulai Zhang ,Matthew Tsang ,Mark Knakstet ,Mihael Turner ,Shane Latham ,Euan Maaulay ,Rhys Pithers

a ARC Training Centre for M3D Innovation,Research School of Physics,Australian National University,Canberra,ACT,2601,Australia

b Department of Materials Physics,Research School of Physics,Australian National University,Canberra,ACT,2601,Australia

c Anglo American Steelmaking Coal,Brisbane,QLD,4000,Australia

d SCT Operations Pty Ltd.,Wollongong,NSW,2500,Australia

Keywords: Cleat separation Cleat statistics Feature extraction Discrete fracture network (DFN) modeling

ABSTRACT Cleats are the dominant micro-fracture network controlling the macro-mechanical behavior of coal.Improved understanding of the spatial characteristics of cleat networks is therefore important to the coal mining industry.Discrete fracture networks (DFNs) are increasingly used in engineering analyses to spatially model fractures at various scales.The reliability of coal DFNs largely depends on the confidence in the input cleat statistics.Estimates of these parameters can be made from image-based threedimensional(3D)characterization of coal cleats using X-ray micro-computed tomography(μCT).One key step in this process,after cleat extraction,is the separation of individual cleats,without which the cleats are a connected network and statistics for different cleat sets cannot be measured.In this paper,a feature extraction-based image processing method is introduced to identify and separate distinct cleat groups from 3D X-ray μCT images.Kernels (filters)representing explicit cleat features of coal are built and cleat separation is successfully achieved by convolutional operations on 3D coal images.The new method is applied to a coal specimen with 80 mm in diameter and 100 mm in length acquired from an Anglo American Steelmaking Coal mine in the Bowen Basin,Queensland,Australia.It is demonstrated that the new method produces reliable cleat separation capable of defining individual cleats and preserving 3D topology after separation.Bedding-parallel fractures are also identified and separated,which has historically been challenging to delineate and rarely reported.A variety of cleat/fracture statistics is measured which not only can quantitatively characterize the cleat/fracture system but also can be used for DFN modeling.Finally,variability and heterogeneity with respect to the core axis are investigated.Significant heterogeneity is observed and suggests that the representative elementary volume (REV) of the cleat groups for engineering purposes may be a complex problem requiring careful consideration.

1.Introduction

Cleats are the dominant micro-fracture network controlling the macro-behavior of coal (Bieniawski,1968).Improved characterization of various cleat properties including orientation,spacing,intensity,and aperture is therefore critical to understanding of the coal behavior and defining the scale of representative elementary volume (REV) needed for engineering analyses.In particular,a systematic characterization of the various cleat groups in a coal specimen is needed for quantifying their influence on mechanical properties (Wang et al.,2019).While previous studies of coal strength scale effects have focused on correlations with coal rank and brightness(Medhurst and Brown,1998),the emergence of new technologies in discrete fracture networks (DFNs) (Dershowitz,1984;Dershowitz and Einstein,1988;Dershowitz and Herda,1992) and discontinuum numerical modeling methods,such as the synthetic rock mass(SRM)method(Pierce et al.,2007;Cundall et al.,2008;Ivars et al.,2011;Tsang,2021),has created opportunities to study coal strength scale effects explicitly from the constitutive intact coal and cleat networks.However,the acquisition of the spatial properties of coal cleat networks for input into DFNs has historically relied on trace measurements from the surfaces of coal core.Although some researchers have applied advanced statistical methods to infer three-dimensional (3D)variation of cleat spatial properties internally within the core(Scholtès et al.,2011;Poulsen and Adhikary,2013),the resulting cleat networks are theoretical and a need for deterministic,explicit 3D mapping of real cleat networks remains.

X-ray micro-computed tomography (μCT) (Knackstedt et al.,2009;Cnudde and Boone,2013;Golab et al.,2013;Wildenschild and Sheppard,2013),which is non-destructive and able to image relatively large samples at high resolution,has been proven to be an effective tool for quantitative investigation of coal cleat networks in 3D(Golab et al.,2013;Ramandi et al.,2016a,2022;Mathews et al.,2017).A workflow for extracting coal cleats,including sample preparation,image acquisition,and image processing has been established (Ramandi et al.,2015;Mostaghimi et al.,2017).The cleat extracted from μCT images are typically a complex,interconnected network that cannot be used directly for the derivation of fracture intensity metrics for input to DFN modeling.Therefore,a key step after the initial cleat network extraction from μCT images is the separation of the network into individual cleat groups from which the key fracture metrics can be measured.Although image processing-based methods for cleat separation have been reported(Jing et al.,2016;Busse et al.,2017),there is a limitation that the 3D spatial continuity of individual cleats has not been considered.As a result,longer,more dominant cleats tend to be unrealistically broken at their intersecting points with shorter,less dominant cleats,which biases statistics extraction.Another issue with the previously reported methods is that they were designed to separate relatively simple cleat systems,i.e.the systems are comprised of only two groups of orthogonal cleats.Significant difficulties are encountered when dealing with complex 3D systems where more than two cleat groups are presented and new methods are needed for dealing with such cases.

In this study,feature extraction(Chen et al.,2016),a widely used technique in computer vision and image processing,is used for complex coal cleat separation from 3D X-ray μCT image.This technique has been successfully used to extract simple structural features including edges(Marr et al.,1980;Torre and Poggio,1986)and corners(Harris and Stephens,1988).It is also a key component of deep convolutional neural networks (CNNs) (Aloysius and Geetha,2017;Rawat and Wang,2017;Wang et al.,2021;Jackson et al.,2022;Tang et al.,2022) where numerous complex and abstract features are extracted from input images through multiple convolutional layers.Although the CNNs are powerful and capable of dealing with complex problems,for example the image classification(Krizhevsky et al.,2017;Lee and Kwon,2017),the structure of multiple convolutional layers(for deep feature extraction)is not used herein as previous research has indicated that coal cleats are approximately thin planar 3D objects (Ramandi et al.,2015;Jing et al.,2016) which are explicit and can potentially be captured by shallow feature extraction.In this study,convolutional kernels(filters) representing explicit cleat features of the coal sample are built and convolutional operations on 3D coal images are undertaken for cleat separation.This approach is not only computationally affordable when dealing with large 3D datasets but also ensures that accurate cleat statistics can be obtained for generating reliable DFNs.

The main objective of this study is to introduce a new image processing method,capable of separating distinct coal cleat groups from complex,interconnected natural cleat systems while preserving their spatial continuity for use as the DFN input to 3D SRM models.The new method is applied to a case study about a coal specimen from an Anglo American Steelmaking Coal mine in the Bowen Basin,Queensland,Australia.Based on cleat separation,key cleat statistics are measured.Finally,the anisotropy and heterogeneity of the cleat system with respect to varying fracture intensity metrics along the core axis are demonstrated and the REV problem is found to be highly complex and requiring careful consideration for treatment in engineering analyses.

2.Material and methods

2.1.Sample preparation and image acquisition

In this study,a 100 mm long,PQ-sized (80 mm diameter) coal sample was acquired from an Anglo American Steelmaking Coal mine in the Bowen Basin.The Bowen Basin is one of the world’s largest reserves of steelmaking coal and is of great economic significance,hosting 48 operational coal mines as of 2011.The 3D μCT images of the coal specimen were acquired at the Australian National University(ANU)CTLab in Canberra,Australia.The specimen was firstly scanned at the as-received moisture state(referred to as dry state)and a dry tomogram was obtained.Then a wet tomogram was scanned after saturating the sample with a contrast fluid that was 1.5 M Sodium Iodide(NaI)mixed with 1 M Potassium Chloride(KCl),as used by Ramandi et al.(2016a).For both dry and wet scans,the voxel size was 36 μm,which resulted in a high resolution of 2200×2200×2800 voxels for a single tomogram.To date,this is the largest coal sample that has been analyzed with this method and the purpose of using such a large sample is to demonstrate the ability of the method to characterize coal at a scale relevant to typical engineering problems.

2.2.Image processing and 3D visualization

The purpose of this step is to extract the whole cleat/fracture network from the images,which is going to be the input to the cleat separation process.The general workflow is shown in Fig.1.Details of each step can be found at Ramandi et al.(2016a)and Mostaghimi et al.(2017).Firstly,the dry and wet tomograms were registered(brought into geometric alignment (Latham et al.,2008)) so all voxels coincide in both tomograms.Then a difference image was built by subtracting the attenuation (or grayscale) in the dry from the wet tomogram.The voxels that exhibit no difference in attenuation are solid regions.Macro-pores(＞36 μm)exhibit the largest difference in attenuation.Other pairs of voxels exhibit smaller attenuation differences;these are sub-voxel porous regions(＜36 μm) and the attenuation difference measurement is a direct estimate of the porosity of each voxel (Golab et al.,2010).If the porosity is a cleat/fracture,the attenuation difference is a measure of the aperture.This is the basis of the aperture estimation method which will be discussed in Section 2.4.

Fig.1.Image processing workflow for preparing input to the cleat separation method.

Cleat extraction/segmentation was carried out on the difference image.It should be noted that,since cleat segmentation here is only for preparing data for cleat separation,not for cleat aperture measurement (Section 2.4),precise segmentation is not required.The aim is to segment as many cleats as possible.Oversegmentation might occur but this does not affect the final results because the cleat phase will be skeletonized so that all the cleats are presented as one-voxel thick.The isolated cleat phase,i.e.cleat fragments due to incomplete extraction,was removed after segmentation.All the image processing steps were done using MANGO (Sheppard et al.,2004;Varslot et al.,2011),a 3D image processing tool box developed at the ANU.

2.3.Coal cleat separation method

Inspired by feature extraction techniques (Nevatia and Ramesh Babu,1980) and CNNs (Shin et al.,2016),an image processing method using convolution operation and thresholding is developed for separating cleats in 3D images of coal samples.Different from other methods,e.g.two-dimensional (2D) methods that separate two orthogonal groups of cleats by first finding and then removing the intersection points(Busse et al.,2017),the present method uses the concept of feature extraction and treats each individual cleat as a 3D object.

Mathematically,a convolution operation is the point-wise dot product between two matrices having the same size.As shown in Fig.2,where a 2 × 2 kernel is convolved across a 3 × 3 input,the kernel slides along the input and for each 2×2 sub-region(in green color) of the input a convolution operation is performed.A kernel can be designed to represent a type of feature so it can extract such features out of an image by convolution.As shown in Fig.2,the input can be thought of having two features,which include one diagonal line and a vertical line.After convolution with the kernel,the diagonal line is strengthened in the output(larger numbers on the diagonal) since the kernel represents a diagonal feature.

Fig.2.An example of convolution operation between a 3×3 input and a 2×2 kernel.Four steps are required to derive the 2×2 output.At each step,the kernel is convolved with a 2 × 2 sub-region (in green color) of the input.

Finding kernels for extracting different types of coal cleat/fracture is relatively straightforward because the coal cleats have simple features:(1)they approximate planar surfaces;and(2)they have a limited number of orientations and thus can be approximately grouped by their orientation.For the coal sample used in this study,slice-by-slice visual examinations of the 3D μCT image(see Fig.3) suggest that it roughly has four groups of discontinuities.Note that here the term discontinuities is used instead of cleats since not all discontinuities are cleats by definition(Rodrigues et al.,2014).From the cross-sectional slices (i.e.tomographicx-yplanes),three groups exist and are orientated in three directions:a minor group(green lines)that roughly sub-parallel tox-zplane;and two major group(blue and yellow lines,respectively)that sub-parallel toy-zplane but distinct from each other.They are all orthogonal to the bedding (the tomographicx-yplane) and therefore are cleats.The 4th group can be identified from vertical(x-zory-z)planes,as indicated by purple lines in Fig.3d.Since they are parallel to the bedding,they will be referred to as beddingparallel fractures hereafter.

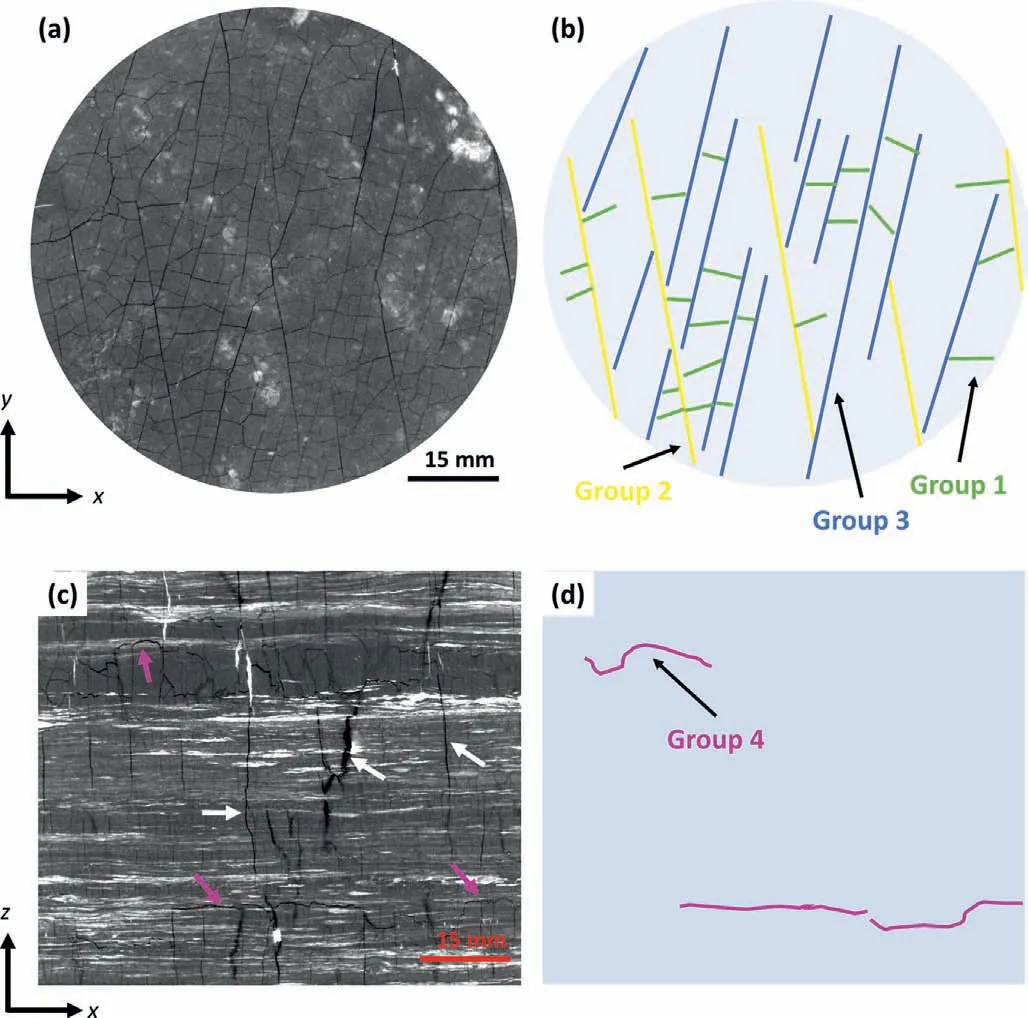
Fig.3.Upper row,(a) one x-y slice of the dry 3D X-ray μCT image of the coal sample and (b) a schematic model of the cleats shown in the μCT slice.Three groups of cleats can be identified (represented by three colors)in x-y plane,which are groups 1,2 and 3.They are perpendicular to x-y plane.Lower row shows the same analysis as the upper row but in x-z plane.Another group of fractures (group 4) is identified in this plane (indicated by purple arrows,lines) and they are parallel to x-y plane,but perpendicular to x-z.White arrows in inset(c)indicate cleats of group 1 or 2 or 3.Note,only a small number of cleats are selected for illustrating in inset(c)and(d).x-,y-and z-directions are the tomographic axis directions.

Based on these observations,the present method uses five kernels (see Fig.4) to separate the coal cleat/fracture system as shown in Fig.3 and each kernel represents a 3D planar surface with a specific orientation.The first step is to separate groups 2 and 3 from group 1;and the workflow is illustrated in Fig.5 using a simple 2D example in which case cleats are represented by 1.The vertical cleat represents one from group 2 or 3 and the horizontal cleat represents one from group 1.Then kernel #1,which represents a vertical line in 2D,is convolved across the input.Then in intermediate output 1,it is clear that the pixels that correspond to the vertical cleat are highlighted by larger numbers as a result of convolution.At the last step,a thresholding using a cut-off of 2 is applied to getting rid of other signals and keep the vertical cleat only.Similar steps can be used to derive the horizontal cleat using kernel#2,which represents a horizontal line in 2D.

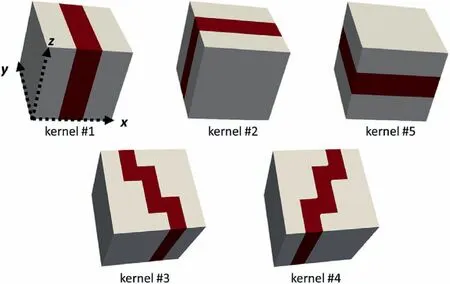
Fig.4.A summary of all the kernels that are used in the present method,shown in 3D.Cleats are represented by red color and non-cleat by white.

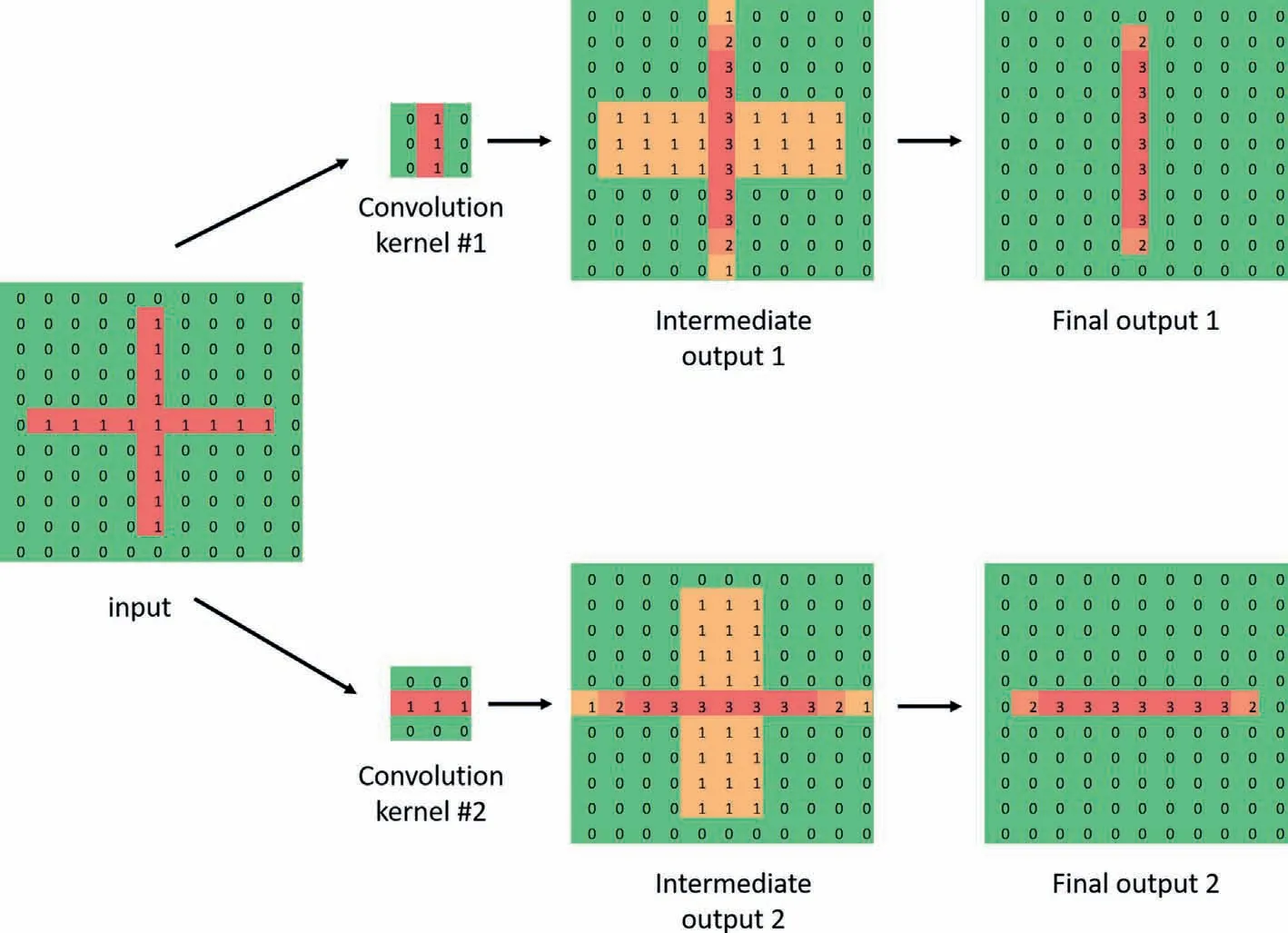
Fig.5.A 2D example showing how to separate two orthogonal cleats using convolution kernels #1 and #2,both are 3 × 3.

Kernels #1 and #2 are best used to separate cleats that are(nearly) orthogonal.For separating groups 2 and 3 as in Fig.3,another two kernels are used,i.e.kernels#3 and#4 in Fig.6 in a 2D case.This time the kernels represent relatively more complex features than kernels #1 and #2 due to the nature of the cleats,and they are also of larger size,i.e.5 × 5 as opposed to 3 × 3.The 2D example in Fig.6 shows that good separation is achieved using a threshold value of 4.Group 4,the bedding-parallel fractures,can be separated from the rest using kernel #5 following the sample procedures as illustrated in Figs.5 and 6.It is important that the kernels in Fig.4 are specially designed for the particular cleat network being studied and they serve as examples of building kernels from cleat features.Customized kernels may be needed for a different cleat network,but for those commonly seen cleat systems,e.g.orthogonal face and butt cleats,kernels #1 and #2 are sufficient.Depending on the placement of the sample on the CT stage in a tomogram,there may not be a group of cleats that are right along a tomographic axis plane (e.g.x-y,y-zorx-z).It is recommended to conduct a rotation of the entire 3D tomogram to make one major group of cleats along a tomographic axis plane,so that it can be separated by kernel #1 or #2 or #5.

Fig.6.A 2D example showing how to separate two cleats having an angle less than 45° using convolution kernels #3 and #4,which both are in size of 5 × 5.

2.4.Calculation of cleat statistics

Typical statistics for quantitatively describing cleats include cleat orientation,size,shape,spacing and intensity (Dershowitz and Einstein,1988),with reliable statistics being a prerequisite for generating realistic DFNs.In this section,the methods used for extracting statistics related to cleat orientation,intensity,spacing and long and short principal axis length are explained.For cleat orientation,each cleat was treated as a 3D object and its normal vector was calculated from the best fitting plane of the object.Fisher coefficient (Fisher,1953;Fisher et al.,1993) measures the dispersion in fracture orientations and serves as an important parameter in DFN modeling.It is also calculated for each cleat group and all groups together.The Fisher coefficient is calculated by(Wang,2005;Michelena et al.,2013):

whereKis the Fisher coefficient,andis the magnitude of the mean vector of all the unit normal vectors of the cleats.

The 3D cleat intensity metrics includingP30,P32andP33were measured with their definition adopted from (Sanderson et al.,2015),whereP30is the cleat number per unit volume of sample,P32is the cleat area per unit volume of sample,andP33is the cleat volume per unit volume of sample.Cleat area was calculated using MATLAB® function regionprops3.Length of long and short principal axes also used regionprops3.Although each cleat gives lengths of the three major axes of the ellipsoid that have the same normalized second central moments as the cleat region,only the two greater ones will be reported herein,i.e.the long and short principal axes.This is because that a single cleat is approximately in a 2D plane and the 3rd dimension can therefore be ignored.For spacing measurement,grid lines along the coordinate axis (e.g.xory-axis)were used for simplicity.For the example in Fig.7,spacingSbetween cleat C2 and C4 isS=Lcos α,whereL=y1-y2and α is the angle between red and black dash lines which can be approximated by the average orientation of the cleats in this slice.

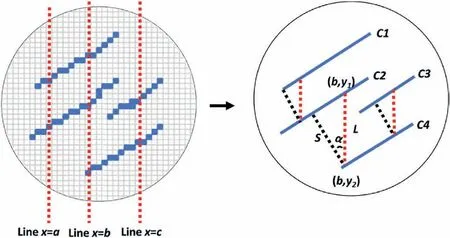
Fig.7.Schematic diagram illustrating cleat spacing measurement.Blue pixels and lines represent the coal cleats;Red dash lines represent grid lines;(b,y1) and (b,y2) are the coordinates of the intersecting points between grid line x=b and cleats C2 and C4,respectively;and L is the distance between the two intersecting points.

The aperture of individual cleats for calculation ofP33was estimated based on grayscale values using a saturation-porosity method (Zhang et al.,2017,2018,2021).This method does not rely on segmenting cleats/fractures from other phases and therefore is able to provide a satisfactory estimation of cleat aperture to a sub-voxel resolution.Zhang et al.(2021) used this method to estimate the aperture of intergranular cracks of a Carrara marble specimen.Although the apertures were only about 1/10 of the voxel size,the estimation matched well with measurements from highresolution scanning electron microscopy (SEM).Another example can be found in Sok et al.(2010).For the first step of this method,the net increase in grayscale (or attenuation) value of a well resolved pore voxel after saturation with contrast agent is found,which is ΔI.Then the total increased grayscale value associated with a cleat,ΔIt,is calculated and converted into cleat volume byV=ΔIt/ΔI.Lastly,cleat aperture μ is obtained by μ=V/Sc,whereScis the surface area of the cleat.This method approximates a cleat by a thin cuboid and a single aperture value is estimated per cleat,ignoring the variation of aperture within a single cleat.Other methods for cleat aperture estimation from images have been suggested by Ramandi et al.(2016b).

3.Results and discussion

3.1.Cleat extraction

Registeredx-yslices from the dry and wet μCT tomograms and the corresponding difference image and segmentation are shown in Fig.8 to show the result of cleat extraction.It is clear that if using the dry tomogram only,cleats at voxel/sub-voxel scale are not well resolved due to narrow cleat aperture and the relatively large voxel size,36 μm.It is also found that there is a fairly large amount of minerals in the coal matrix,shown by brighter regions in the dry tomogram.When the cleats exist in the brighter regions where minerals are presented(e.g.the area inside the red frame in Fig.8),they become harder to identify due to image blurring effects which increase the grayscale values of the cleats.In the wet tomogram,contrast between cleats and matrix is enhanced using the contrast agent,giving a much stronger signal for identifying the cleats.With the assistance of a difference image(wet minus dry),cleats are well captured even for those at sub-voxel scale and/or inside mineral regions.

Fig.8 . x-y slices from the registered dry and wet tomograms and the corresponding difference image and cleat segmentation.Enlarged images of the red frame area are given in the 2nd row.The images illustrate how minerals blur the cleats and the quality of segmentation after using a difference image.

3.2.Cleat separation

Fig.9 shows the cleat separation result of the 2D slice as shown in Fig.8.It illustrates that using the method in Section 2.3,the complex cleat network can be separated into individual groups of cleats that have similar orientation.Cleats of group 1 are mostly alongx-zdirection.Although they are shorter compared with those of groups 2-3,they seem to have a larger cleat intensity.Both groups 2 and 3 are approximately alongy-zdirection.Group 3 may have the least cleat intensity and therefore the largest spacing.In the literature,the predominant cleats are called face cleats and formed first;the shorter ones intersecting the face cleats at about 90°are called butt cleats and formed later (Pattison et al.,1996;Laubach et al.,1998).According to these conventions,cleats of groups 2 and 3 can be seen as the face cleats and those of group 1 as the butt cleats.It is suggested that the occurrence of three distinct cleat groups could reflect formation under complex stress conditions in the Earth’s crust,similarly to the influence of the intermediate stress axis on polymodal shear fracturing (Healy et al.,2015).

Fig.10.3D visualizations of separated cleat groups 1-3 from different angles.Group 1 is in green,Group 2 in yellow,and Group is in blue.All images show the same section(18 mm thick,80 mm diameter) of the whole dataset for clear visualization.

Fig.11.3D visualizations of some cleats with large extent in z-direction in the 100 mm long sample.Three cleats are shown: one of group 1 (in green),one of group 2 (in yellow) and one of group 3 (in blue).(a) and (b) show the same cleats but from different angles.

The 3D visualizations of separated cleats(groups 1-3)are given in Fig.10,showing the 3D shapes of individual cleats and their spatial relationship.One distinct feature of group 1 is that most of them seem to be deviated from flat planes.Due to the curvature,they have varying orientation although they approximately subparallel tox-zplane.Another feature is that cleats of group 1 sometimes cut through groups 2 and 3,i.e.they do not always terminate when meet cleats of groups 2 and 3.This might suggest that the length of the butt cleats(the dimension inx-yplane for our case) is not always the spacing of the face cleats.However,it is difficult to distinguish whether the crossover configurations are original or extension fractures from the butt.Compared with that of group 1,cleats of groups 2-3 are much flatter and almost have no curvature.Groups 2-3 are also larger in size than group 1 in general and our analyses suggest that they extend beyond the sample size.Much larger samples are needed to derive a full picture of these cleats.Although there are cleats in the middle of the sample without reaching the boundary,it is difficult to conclude if they are just fragments of larger cleats that were not fully extracted.Some larger cleats of groups 1-3 are selected to show their extent inzdirection in Fig.11.It can be seen that the face cleats may have a fairly good continuity inz-direction;the yellow cleat of group 2 is about 70-mm long inz-direction,almost across the whole sample.Although the butt cleats are generally smaller than the face,they may also have a large extent inz-direction;the green(butt)cleat in Fig.11 is about 50-mm long inz-direction.Although there are openings and holes in the cleats as a result of incomplete cleat extraction (see Section 3.1),each individual cleat remains a continuous 3D object.

Fractures of group 4 mainly parallel to bedding plane(x-yplane)and they are shown in 3D in Fig.12 together with the other groups.It is clear from 3D visualizations that group 4 mainly occurs at two depths of the imaged sample.Group 4 fractures seem smaller in size compared with those in other groups,and their surface may be curved to some degree.The 3D visualizations of the cleats in Figs.10-12 are made by an open-source software,MeshLab(Cignoni et al.,2008),which can also generate quality meshes that can be put into SRM models(Pierce et al.,2007;Cundall et al.,2008;Ivars et al.,2011).

The quality of the cleat separation is demonstrated in Fig.13.It shows that the separation is accurate and most of the cleats keep their integrity after separation,i.e.the long cleats of groups 2-3 are not broken at their intersecting points with group 1.The geometry of individual cleat was also preserved to a large extent.As shown in the separation results,cleats with gentle changes in orientation were well captured by the proposed method.The curvature of such cleats was preserved after separation although the kernels (see Fig.4)only represent simple planar objects with no curvature.One minor drawback of the new method is also noticed.It is that since the kernels are all designed to capture simple 3D planar objects,a cleat that has a sharp change in orientation due to curvature may be divided into different parts (blue arrows in Fig.13) or may lose some sections(black arrows in Fig.13).This issue is minor because the 3D image shows that cleats having a sharp change in orientation are rare.The other point that is worth noticing is that because this new method (like most of the methods in the literature) separates cleats by orientation without any physical constraint,the cleats that are classified in the same group may be intrinsically different.For instance,the red arrows in Fig.13 indicate a shorter cleat/fracture that is include in group 3 (face cleats),although it may have formed by a different mechanism.

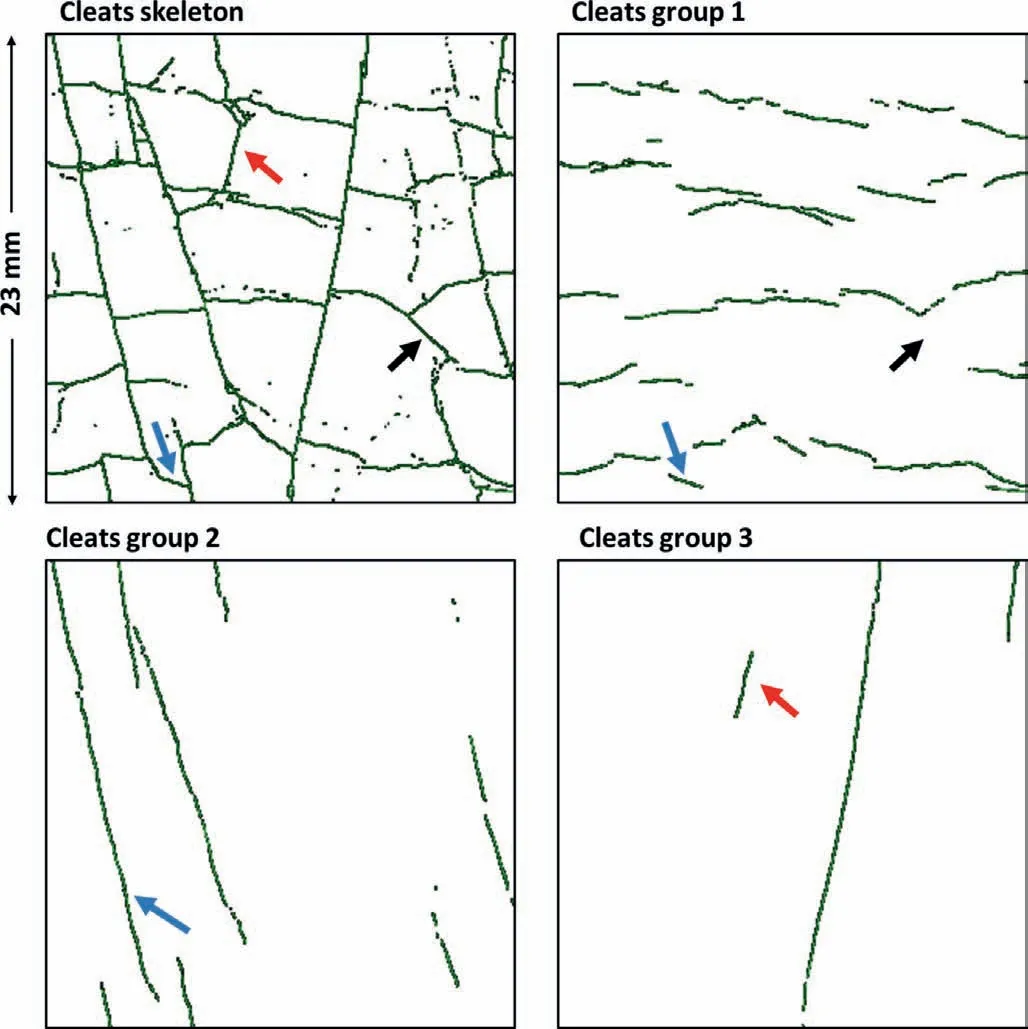
Fig.13.Quality check of cleat separation of the areas as indicated by black frame in Fig.9.The blue arrows indicate a long cleat that changes its orientation at one end is separated into two parts.The black arrows indicate a curved cleat lost a section after separation.The red arrows indicate a cleat/fracture that is put into the group of face cleats but may have formed by a different mechanism.

3.3.Cleat statistics

An equal area stereonet showing the orientations and clustering of cleats mapped from the μCT scan is presented in Fig.14.Like what is already seen from the images(e.g.Figs.3,8 and 9),each of the four groups has a distinct range of orientations.Group 1 approximately parallel to the tomographicx-zplane and group 4 approximately parallel tox-yplane.Groups 2 and 3 are steeply dipping,oriented sub-parallel toy-zplane.Note that orientations have been reported with respect to the tomographic axes and not cardinal axes as the core is not oriented during drilling of the nominally vertical borehole.

Fig.14.Equal area stereonet showing poles of four cleat groups with great circles representing the mean principal orientation for each group.Note that orientations are plotted relative to tomographic axis of μCT image as the core was not oriented.

The calculated Fisher coefficients for each group are summarized in Table 1.Since largerKvalues indicate lower dispersion in orientations and vice versa,groups 2 (K=214) and 3 (K=162)have relatively more uniform cleat orientation than group 1 (K=37).This indicates that during the formation of butt cleats (group 1),the growth direction is more affected by local heterogeneities,which may include stress field and mineral composition variations(Pattison et al.,1996).On the other hand,the face cleats(groups 2-3)are mainly controlled by the stress pattern at larger scales.K=3 for all the groups combined suggests a heterogeneous cleat system in terms of orientation.

Table 1Fisher coefficients.

The 3D cleat intensity measures of the whole imaged sample are shown in Fig.15.Of particular importance is the volumetric fracture density,P32,which is critical for mechanical REV analysis(Dershowitz and Herda,1992).SinceP32cannot be measured directly with conventional field mapping or core logging methods,it is typically estimated indirectly from one-dimensional (1D,i.e.P10or lineal fracture intensity) or 2D (P21or areal fracture intensity) intensity metrics using conversion factors derived from stereology(Wang,2005).For the cleat network that was directly mapped from the μCTscan model and separated using our new method,equivalent values ofP10andP21were estimated by simulating 1D traces and 2D planes through a cubic subset of the model and then applying the conversion factors in Wang(2005).The results of these simulations are shown in Fig.16,and it can be seen that conversions fromP21toP32are relatively satisfactory when the sampling plane is large.At the maximum possible sample plane size,the indirectly-estimatedP32has a median value of 385 m-1,compared with the directly measuredP32of 353 m-1.However,the conversion fromP10toP32is less reliable andP32is significantly underestimated even when the trace line reaches its maximum possible length(the median value is 202 m-1).This is inferred to be related to the exclusion of cleat length/persistence in the calculation ofP10.

Fig.15.Distributions of cleat/fracture volumetric intensity measurements.

Fig.16.Results of simulations on converting from(a)P21(length of cleats per unit area of sampling plane)and(b)P10(number of cleats per unit length of trace line)to P32.Results are shown by box and whisker plots with outliers not shown.Simulations are based on a 50 mm × 50 mm × 50 mm subset.

Cleat size anisotropy was quantified by comparing the lengths of the long and short principal axes of the fitted ellipses for individual cleats by group (see Fig.17).It can be seen that the fractures of group 4(bedding)are the smallest(least persistent)exhibiting the least size anisotropy.For the two face cleat groups(groups 2 and 3),the sizes of the long axes approach the diameter of the sample,indicating that the REV is likely greater than the sample dimensions of 80 mm × 100 mm.The butt cleats in group 1 tend to terminate against the face cleats of groups 2 and 3 and with length therefore close to the face cleat spacing (see Fig.18).

Fig.17.Distributions of long and short principal axis lengths for (a) group 1,(b) group 2,(c) group 3,and (d) group 4 demonstrating cleat/fracture size anisotropy.

Fig.18.Distributions of spacing for (a) group 1,(b) group 2,(c) group 3,and (d) group 4.

Spacing measurements for all cleat/fracture groups are shown in Fig.18.The butt cleats of group 1 exhibited the smallest spacing(＜10 mm)while the face cleat group 3 exhibited the largest(up to 30 mm).These measurements agree with that observed in the images (see Fig.9) and are also in general agreement with measurements on Permian coals from the Bowen Basin,Australia(Pattison et al.,1996).The spacing of bedding fractures in group 4 showed a distinct bimodal distribution,indicating separate bedding groups likely relating to sedimentation that had not been identified from other metrics.

Cleat aperture measurement(see Fig.19)shows a wide range of aperture of the individual cleats,from a few μm up to 60 μm.Most of the face and butt cleats in groups 1-3 have an average aperture of 8-9 μm while the bedding fractures in group 4 are larger(around 25 μm in average) and more variable.This findings are consistent with other Bowen Basin samples (Ramandi et al.,2016b).

Fig.19.Cleat/fracture aperture measurement for (a) group 1,(b) group 2,(c) group 3,and (d) group 4.

3.4.Vertical heterogeneity and REV analysis

Since the new method works efficiently on a large 3D dataset,cleat separation and quantitative characterizations were carried out on the full dataset.This enables analysis of vertical variations of the complex 100 mm long cleat system,which is rare because most of the previous image-based works on coal cleat characterization used 2D surface images or 3D images of small volumes.Here,some selected properties of the extracted cleat system are quantified perx-yslice and are plotted in Fig.20,which shows significant variations of the 100 mm-long system from top to bottom.For cleat spacing (see Fig.20a),it shows that groups 1 (butt cleats) and 2(face cleats) have more homogeneous spacing alongz-axis than group 3 (face cleats).

Fig.20.Vertical variations of selected properties of the cleat system.All selected properties are quantified on a per x-y slice basis and are plotted against slice number in z-axis.(a)Average spacing;(b)cleat density in number of voxels;(c)red markers are areal percentage of minerals per slice and black markers are cleat density per slice,after normalized by the maximum cleat density of all slices;and (d) a vertical slice of the sample showing mineralization (in bright) and cleats (in black).

Fig.20b shows the high variability of cleat density(measured in voxels) for all groups with respect toz-axis.As seen from the 3D visualizations in Fig.12,fractures of group 4(bedding)only occur in two intervals and return zero density outside of these intervals.Groups 1-3 show clear variations in cleat density with no continuous interval of stable cleat density,although group 1(butt cleats)demonstrates the highest variability.As shown in Fig.8,the coal sample has a significant amount of mineral matters and its areal percentage of each slice is quantified and plotted in Fig.20c.In the same figure,the total cleat/fracture density (all four groups combined)of each slice is also plotted and normalized to the maximum cleat density of all slices.The reason for plotting two together is that visual inspections of the tomograms frequently gives the impression that the existence of mineral matter may have prohibited the development of cleats.Fig.20c illustrates the negative correlation between mineral presence and cleat density.

Two distinctx-yslices demonstrating vertical variations of the cleat system are shown in Fig.21.The upper slice(#1040)has a high mineral matter content of around 50% and a low cleat density that is only about 20% that of the highest slice.The corresponding cleat segmentation shows that only the major face cleats are captured and the areas between the face cleats where butt cleats should have occurred are mostly solid.The lower slice(#2340)is relatively clear of mineral matters and the segmentation has a much higher cleat density,about three times of slice#1040.However,it is important to note that the presence of mineral heterogeneity does not necessarily disrupt the cleats in vertical direction.As shown in Figs.11 and 20d,some cleats continue across the mineral zones and maintain their continuity inz-axis.

Fig.21.Two example x-y slices from the dry tomogram and corresponding segmentation.Slice#1040 is an example of high mineral matter content and less cleat density while slice#2340 is the opposite of #1040.

Plotting theP32of each cleat group against sample volume reveals a different local REV for each cleat/fracture group(see Fig.22).This is in good agreement with the observations from Fig.20 and indicates significant heterogeneity between cleat groups.Group 1(butt cleats) has the largestP32value of about 150 m-1,with REV convergence occurring at a sub-volume side length of around 40 mm.Group 3(face cleats)has a similar REV to the group 1 butt cleats but has a lowerP32value of about 50 m-1.For groups 2(face cleats) and 4 (bedding) the REV appears to be larger than the subset,i.e.convergence did not occur even at the largest possible sampling size.

4.Conclusions

In this paper,a new image processing method for 3D X-ray μCT images is introduced,which is able to separate a complex cleat system into individual cleat groups with similar orientation.This method is based on feature extraction and it is computationally efficient when dealing with large 3D datasets.Another advantage of this method is that individual cleats geometry and spatial integrity are preserved to a high extent after separating from the cleat network,which is critical in assuring extracting precise statistics from the cleats.

The method is successfully applied to an 80 mm diameter and 100 mm long sample.Four groups of cleats/fractures are separated from the whole network of discontinuity.Cleats of groups 1-3 are perpendicular to bedding plane,including two groups of face cleats and one group of butt cleats.The two groups of face cleats are approximately 40°to each other and the butt cleats are roughly perpendicular to the face cleats with a range of orientations.Fractures of group 4,which mainly parallel to the bedding plane and are less reported in previous studies,are also separated.The 3D visualizations of all groups are shown using MeshLab,which can also generate quality meshes that can be directly put into SRM models,e.g.PFC(particle flow code)models(Mas Ivars et al.,2011).The 3D visualizations show that most of the butt cleats (group 1) deviate from flat planes.They do not always terminate at the face cleats,which results in cross intersections with the latter.It is also found that the real size of the face cleats is beyond the size of the 80-mm diameter sample,which suggests that larger samples are needed for precise cleat size measurements.

Coal cleat statistics used for generating stochastic DFNs include cleat orientation,3D intensity,spacing,and length of principal axes.The methods for calculating the statistics are also explained.Comparison between directly measuredP32and convertedP32(fromP10andP21) suggests thatP32converted fromP10underestimates the cleat intensity and should be used with more care.In addition,it shows that the aperture is mostly sub-voxel(＜36 μm)but could be as high as 60 μm.Among the four groups,group 4 has the largest average aperture,group 1 has the smallest,and groups 2-3 are in the middle.The statistics reported here represent the largest coal sample that is ever characterized,to the authors’knowledge.

Vertical heterogeneity of the cleat system is analyzed based on the acquired statistics.Along the 100-mm length of the sample,significant variations of the cleat system are observed.For instance,cleat density per slice could vary by a factor of 5.It is also found that there is a negative correlation between mineral content and cleat density.REV analysis suggests that for all groups,the REV for cleat intensity (P32) is around 40 mm or greater.The heterogeneous nature of coal cleats indicates that the use of cleat statistics measured from small samples needs more care.

Recommended future work to support the practical application of the new cleat separation and characterization methods to the coal mining and coal seam gas industries includes: (1) Incorporation of measured cleat DFNs into SRM discontinuum numerical models;(2) development of empirical correlations between cleat intensity and macro-mechanical and flow properties;and (3)identification of the REV for a range of coals and cleat conditions.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

We acknowledge the funding support from the Australian Research Council,under the ARC Training Centre for Multiscale 3D Imaging,Modeling and Manufacturing.