波流环境中多孔射流三维数值模拟

徐振山,韩 松,张玉玲,陈永平

(1.河海大学港口海岸与近海工程学院, 江苏 南京 210098;2.中国能源建设集团广东省电力设计研究院有限公司, 广东 广州 510663)

排海污水通常以单孔或多孔射流的形式在海水中运动,而多孔逐渐取代单孔扩散器成为污水处置工程的发展趋势,其运动和稀释规律是海岸水动力及水环境研究重点关注的问题。开展波流环境中多孔射流近区运动的研究,有助于丰富射流理论,提高对多孔射流运动和稀释规律的认知,为废水排放工程的环境效应分析提供参考。

陈永平等[11]测量了波浪环境中多孔射流的速度场与浓度场,认为波浪环境的非恒定性会有效提高射流的稀释及扩散能力,波高与波周期的增加都会加速射流轴线速度的衰减。沈小雄等[12]研究了波浪环境中双孔射流的压强分布规律,认为波浪加速了相邻射流的吸附与掺混,并且随着波周期的增大,这种加速会更加明显,射流合并断面将会提前出现。Liu等[13]研究了3种长波(对称、反对称和单侧)激励模式下的平面射流,认为人工激励可以有效地加强涡旋结构从射流近场至远场的演变。Anghan等[14]认为波浪环境中的射流未来研究应集中在直接的数值模拟上,考虑到解析完整流场所需计算量大,则应该更多关注射流近场及部分远场。

丁宏伟等[15]的物理实验表明在波流环境中双孔射流的轴线平均垂向速度衰减规律符合幂函数关系。张玉玲等[16]测量了多孔垂向射流的速度场与浓度场,发现相比于单孔射流,多孔射流各孔“污染物云团”发生重叠,云团更加不明显。基于上述物理实验,本文采用合成涡方法(synthetic eddy methods,SEM)生成边界条件,使用大涡模拟(large eddy simulation,LES)搭建合理的数学模型,进一步探究波流环境中多孔射流的三维运动规律和稀释特性。

1 研究方法

1.1 波流环境中多孔射流数学模型

波流环境中多孔射流大涡模型控制方程为空间平均的纳维-斯托克斯(N-S)方程和浓度标量输运方程。模型在垂向上引入σ坐标解决自由面追踪问题[17]。控制方程采用算子分裂法求解,对流项采用二次向后特征线法和Lax-Wendroff格式平均法离散求解,扩散项采用时间向前差分、空间中心差分格式离散求解,泊松方程利用共轭梯度算法求解。

采用考虑波浪影响的时均水流流速剖面叠加波浪速度分量的方法得到波流水槽入口边界条件,波流入口波面高度和三维速度分量的具体给定公式参考徐振山等[18-20]的研究;采用零梯度条件加修正的人工海绵层的方法得到出口边界条件。采用拉格朗日-欧拉法追踪波浪和水流共存情况下的速度自由表面[21];浓度自由表面边界采用零梯度边界条件。底部速度边界采用可滑移边界来预测第一个网格节点处的速度梯度,采用壁面函数法计算底部切应力;底部浓度边界采用零梯度边界条件。侧向边界处采用不可入边界条件。模型的初始压强按照静压假定给出,浓度初始值为0,x、y、z方向的速度u、v、w初始值均为0,水流存在时,波流水槽沿水深方向的速度分量按照对数分布假定给定。

模型中各项关键参数值均落在合理范围之内。其中紊动放大系数和Smagorinsky常数对射流垂向速度衰减程度有较大的影响,分别取为3.0和0.175较为合适;出口平均浓度分布和紊动普朗特数对射流轴线浓度衰减程度有一定的影响,出口平均浓度分布函数借鉴出口平均速度分布函数,紊动普朗特数取为1.0。

模型计算域长9.0m、宽0.5m、高0.5m,对垂向坐标进行σ变换,可以精确捕捉自由表面的变化。采用4套网格对模型计算域进行划分(表1),分别命名为G1～G4,网格在x、y、z方向非均匀划分,并且在射流口及自由表面附近进行加密。用以上4套网格模拟静水环境中的射流,进行网格敏感性分析。图1为4套网格下射流的垂向速度曲线(图中wc为横断面上最大射流流速,w0为射流出口流速,D为射流管径)。其中G1模拟结果与其他3套网格差异最大,证明射流口的网格划分对模拟结果影响很大。通过对比模拟结果较好的G2～G4,可以发现射流口范围外的网格粗细程度对模拟结果影响很小,相比之下G3拟合效果最好且计算成本较低,所以采用G3网格进行模拟(图2)。第1孔射流布置在距离入流边界2.0m的位置,阻尼区长度占水槽全长的60%。

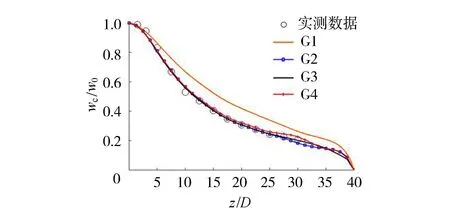
图1 不同网格设置条件下静水射流的垂向速度衰减曲线Fig.1 Vertical velocity attenuation curve of static water jet under different grid settings

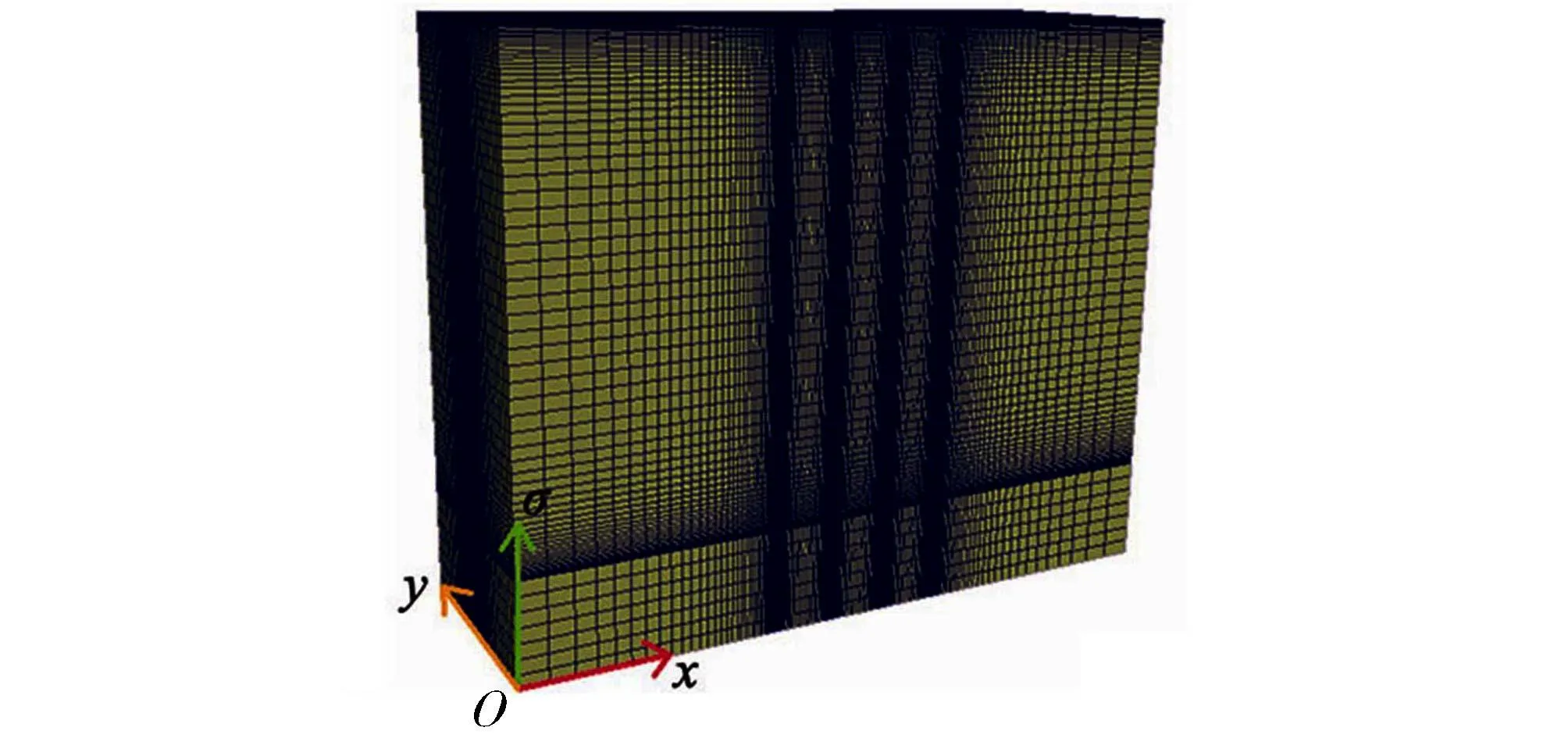
图2 计算域网格划分Fig.2 Grid partitioning of computational domains

表1 网格信息Table 1 Grid information

图3、图4是模型在波流环境中的验证结果(图中c和c0分别为某位置处的时均浓度和射流出口浓度),其中前两个断面z/D=5.0、z/D=7.5速度场与浓度场的模拟结果与试验数据吻合较好。z/D=10.0断面因为波流与多孔射流强烈的相互作用,速度、浓度分布有差异,但模拟结果中速度、浓度分布的展宽和峰值与实测值相差不大。此外,模型在静水、规则波、横流等不同环境中射流的数值模拟结果与实测数据和经验曲线吻合均较好,证明了该模型的合理性和准确性。关于波流环境中射流数学模型的更多介绍和验证结果可参见文献[16,22]。

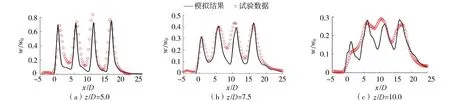
图3 波流环境中不同断面处时均速度验证Fig.3 Verification of time average velocity at different sections in wave-current environment

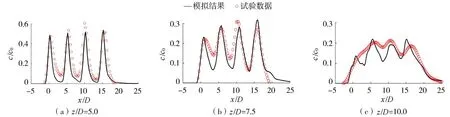
图4 波流环境中不同断面处时均浓度验证Fig.4 Verification of time average concentration at different sections in wave-current environment

1.2 湍流边界设置

湍流射流中脉动和混合主要是由大尺度涡引起的。大尺度涡结构对流场的边界条件及初始条件具有很强的依赖性,而且与主流的相互作用较强。所以在大涡模拟过程中合理地给定射流瞬时紊动边界对于射流发展具有非常重要的意义[23]。合成涡方法是指在入流边界上进行涡的叠加合成,每个涡对入流边界各网格点的作用强度都由形状函数确定,涡的位置与方向随机生成[24-25]。相比其他常用的湍流进口给定方法,合成涡方法可以较大程度地避免紊动衰减,最为简单可行,进口发展段更短,可以得到具有正确统计特性的湍流,且便于修正和操作。

本文数值计算采用合成涡方法生成各向同性的湍流,即令σx=σy=σz,并通过生成明渠入流边界算例验证了该方法的可靠性,同时根据得到的统计特性验证了合成涡方法的有效性,最后用合成涡方法生成射流出口边界,并植入三维大涡数值波流水槽模型中进行射流模拟。

1.3 模拟组次设置

为研究波流环境中多孔射流的三维运动特性以及射流间的相互作用,设置组次B1～B4;为探究孔间距影响并得到所有组次下最优相对孔间距,设置组次D1～D4。在所有组次中,射流出口流速均为68.55cm/s,横流流速均为5.48cm/s。波流环境中多孔射流计算参数见表2。

表2 波流环境中多孔射流计算参数Table 2 Calculation parameters of multiple jets in wave-current environment

2 模拟结果与分析

2.1 波流环境中多孔射流的三维运动特征

以B4组次为例,选取4个典型特征相位的瞬时流场分析多孔射流的运动特性,其中t=0T、0.25T、0.5T、0.75T(T为波周期)分别表示第1孔射流上方波浪水质点处于上跨零点、波峰、下跨零点、波谷相位。图5为y/D=0断面流线分布图,(u2+w2)1/2为断面横向和垂向合成速度。

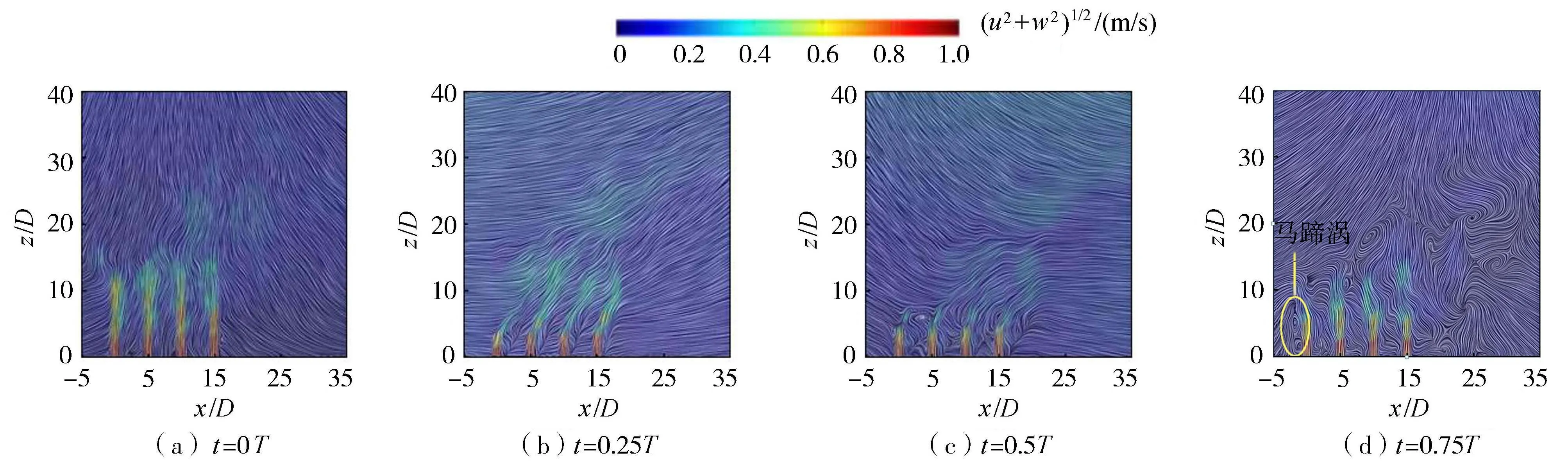
图5 y/D=0断面流线分布Fig.5 Streamline distribution diagram of y/D=0 section

a.在t=0T时刻,波浪水质点垂向速度正向最大,射流拥有较大的垂向动量。环境横流速度的方向和大小与射流差异较大,造成多孔射流迎流面和背流面处剪切层失稳,产生剪切涡,流线在z/D=10.0附近具有明显的偏转;由于横流绕流作用,在第4孔射流背流面下游形成了尾涡,流线从底部偏向前方射流。

b.在t=0.25T时刻,波浪水质点横向速度正向最大,与横流流速叠加,背景流场中横向速度在周期内达到最大值,流场与横流环境中的射流流场非常相似。射流与横流速度比相对较小,横流绕流作用强,射流迎流面和背流面上的剪切涡较为明显;各孔射流的背流面都可以观察到树叶状的流线,是横流绕流后残存水平动量与背流区尾涡平衡的结果。

c.在t=0.5T时刻,波浪水质点垂向速度负向最大,射流动量被大大削减。射流迎流面附近的流线弯曲程度更大,前3孔射流背流区流线杂乱。在z/D=8.0高度附近第1孔射流与第2孔射流发生汇合,产生了较为明显的涡旋,是由于下行的剪切涡与上行的尾涡相遇,使流线发生卷曲。

d.在t=0.75T时刻,波浪水质点横向速度负向最大,与横流发生着强烈的相互作用,射流与环境流场也发生剧烈的掺混,流场中流线混乱,涡旋众多。由于波浪的负向流速略大于横流流速,多孔射流均逆流偏转;横流受到波浪和射流的阻碍作用,围绕第1孔射流形成2个明显的马蹄涡。

图6为x/D=0(第1孔射流位置处)断面流线分布图,(v2+w2)1/2为断面纵向和垂向合成速度。在t=0T时刻,射流与环境流体之间的垂向速度差造成速度断面失稳,周围流线均偏向射流中心;在t=0.25T时刻,以射流轴线为对称中心,形成肾形反向旋转涡对(CVP)的雏形,这是横向紊动射流的一个显著特征,此时射流流线顺流偏转程度最大,红色区域面积较小;在t=0.5T时刻,波浪对射流垂向动量的削弱,导致CVP分布范围缩小,但已形成了2个明显的涡旋,且涡旋位置有所抬高;在t=0.75T时刻,CVP分布范围大大拓展,涡旋中心位置继续提升,在CVP下方还分布着大量马蹄涡。

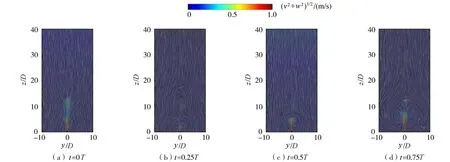
图6 x/D=0断面流线分布Fig.6 Streamline distribution diagram of x/D=0 section

图7为z/D=20断面流线分布图,(u2+v2)1/2为断面横向和纵向合成速度。在t=0T时刻,射流垂向动量较大,流场中同时出现了绕过射流的马蹄涡和射流背流区的尾涡;在t=0.25T时刻,射流顺流偏转程度最大,在z/D=20高度处流场受射流影响较小,流线较为顺直;在t=0.5T时刻,各孔射流上方波浪水质点所处相位不同,横向流速沿程稍有差异;在t=0.75T时刻,因为波流间强烈的相互作用,在x/D>15范围内出现了3个明显的大尺度涡旋结构。

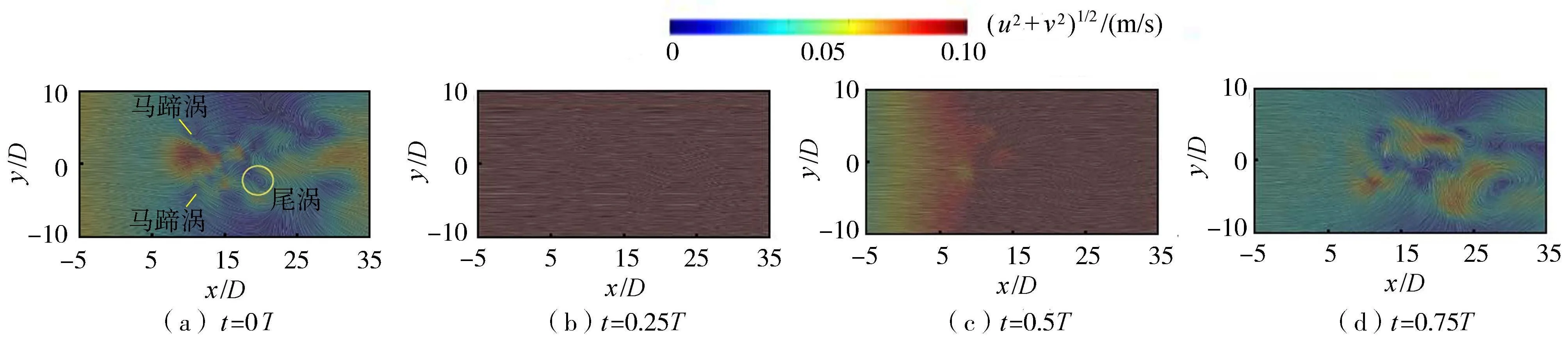
图7 z/D=20断面流线分布Fig.7 Streamline distribution diagram of z/D=20 section

通过对一个波周期内不同断面、不同特征相位下的瞬时流线和涡旋结构的分析可知,流场流线和涡旋分布随波浪水质点的周期变化呈现完全不同的景象:在上跨零点相位,流场和射流与横流速度比较大的横流流场类似;在波峰相位,流场和射流与横流速度比较小的横流流场类似;在下跨零点相位,射流动量明显被削减,流场中涡旋数量增多;在波谷相位,流场中的涡旋结构最为丰富,包括因横流受到射流的阻挡而围绕射流产生的马蹄涡、基于环形剪切层的凯尔文-亥姆霍兹不稳定性在射流迎流面和背流面上形成的剪切涡、因横流扰流作用在射流背流面下游形成的尾涡、因横流扰流作用涡旋断面由圆形变为弯曲的肾形涡、因横流与波浪的相互作用而产生的大尺度强涡旋。射流被环境流体稀释的主要因素是射流近区涡的出现和配对,所以周期性变换的波流流场、大量的涡旋导致射流的紊动和扩散能力增强,这是射流在波流环境中(相比于单一的水流环境)垂向速度衰减更显著、更快速的主要原因。

选取B1～B4组次的时均流场分析波浪强度对射流主轴线速度衰减的影响,这4个组次中射流出口流速与横流流速均保持不变,射流与波浪速度比Rw即可表征当前组次中波浪强度的相对大小。提取B1～B4组次4孔射流的主轴线,计算主轴线上的三维合成速度,图8为B4组次4孔射流沿主轴线的速度衰减曲线。

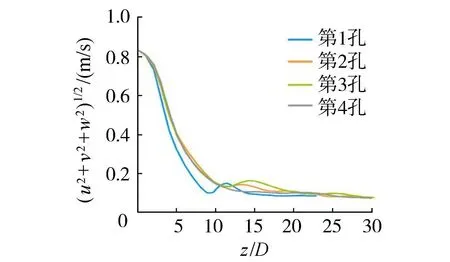
图8 B4组次4孔射流沿主轴线的速度衰减曲线Fig.8 Velocity attenuation curve of four-hole jets along the main axis in group B4

由图8可知,第1孔射流速度沿程衰减最快,其次是第4孔射流,因为在波流动力环境中外侧射流直接与环境流体作用,其稀释扩散速度较快;第4孔射流速度衰减曲线单调递减,其他3孔射流的速度衰减曲线均会形成一个明显的凸起,且上游射流出现凸起的位置均先于下游射流。可以看出第1孔射流流线在速度衰减曲线凸起处(z/D=12附近)形成一个转折点,转折点上游是一段平缓的轨迹线,将其称作弯曲平台,转折点下游第1孔射流逐渐与其他射流汇合。综上可知,弯曲平台及速度衰减曲线中凸起段的形成与下游射流对上游射流的阻碍作用有关;在经历弯曲平台后,射流流线相互汇合;后方射流的阻碍作用使得多孔射流轨迹上速度衰减程度小于单孔射流情况。

对比不同波况下多孔射流时均合成速度沿三维轨迹线的衰减曲线(图9),均遵循波浪强度越大,射流轴线速度衰减越快,即稀释扩散效果越佳的规律;通过对比图中前3孔的射流流线,发现波浪强度越大,弯曲平台越早出现,即表明多孔射流更早地发生汇合,以致汇合位置更低。

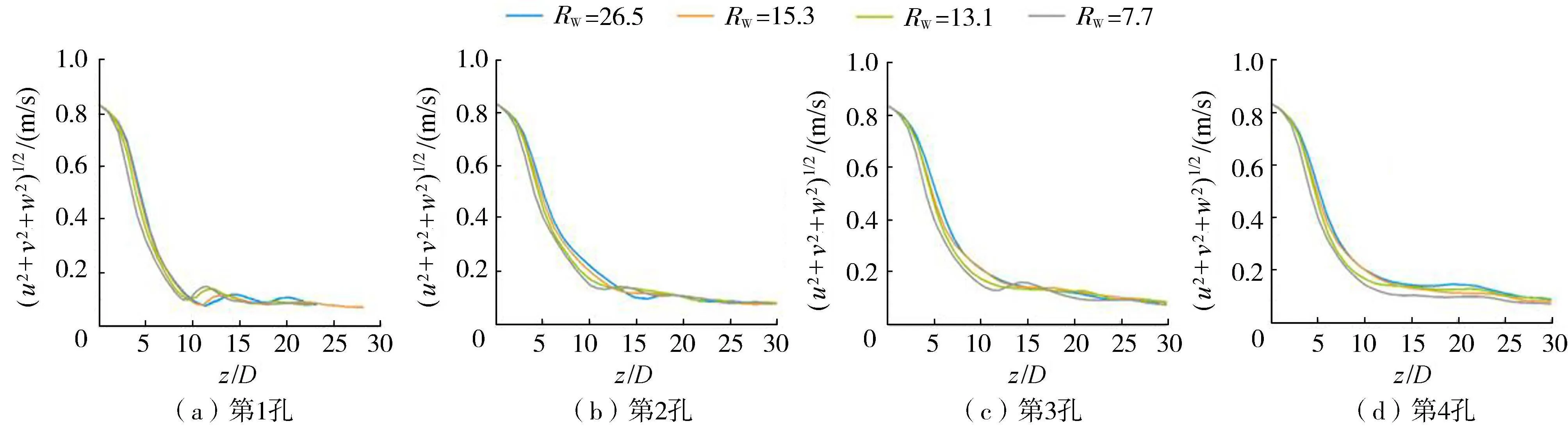
图9 不同波况下多孔射流时均合成速度沿主轴线衰减曲线Fig.9 Attenuation curve of time-average synthetic velocity of multiple jets along the main axis under different wave conditions

2.2 波流环境中双孔射流孔间距对射流扩散的影响

图10为射流口高度处(z/D=0)断面上的流线分布。当相对孔间距s/D=2.5时(s为孔间距),双孔射流距离比较近,只形成了1个尺度较大的马蹄涡;当s/D≥5.0时,各组次断面中双孔射流附近均出现一大一小2个马蹄涡,随着射流孔间距的增大,第1孔射流附近马蹄涡的大小基本保持不变,第2孔射流附近马蹄涡的尺度逐渐增大。

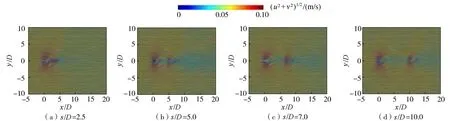
图10 z/D=0断面流线分布Fig.10 Streamline distribution diagram of z/D=0 section

图11为不同相对孔间距双孔射流口连线中点处(x/D=0.5)断面上的流线分布,可以观察到不同孔间距下都出现了成形的CVP结构,但随着孔间距的增大,CVP结构的尺寸和形状略有不同。当s/D=2.5时,CVP位置较低,呈扁平椭圆形;随着孔间距的增大,CVP的形状逐渐变为正圆形;当s/D=10.0时,1对小尺度涡旋逐渐在大尺度涡旋的正上方形成。综上可知,在一定范围内,孔间距越大,多孔射流流场中涡的数量和规模越大,进而导致射流与环境流体之间的相互作用增强。

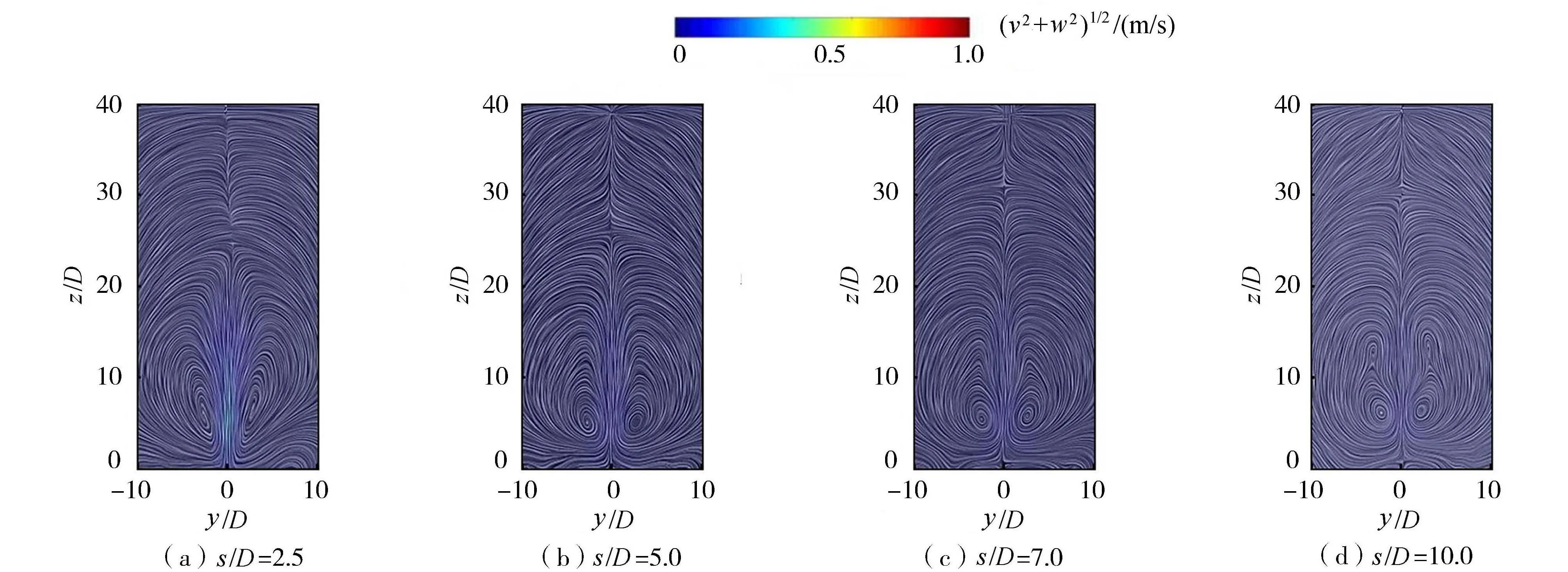
图11 双孔射流连线中点处断面流线分布Fig.11 Distribution diagram of section streamline at the midpoint of two-hole jet connection

在波峰相位下,流场中较容易观察到动量和浓度较大的“污染物云团”,此时双孔射流之间的相互作用为明显。图12为不同相对孔间距波峰相位下的双孔射流平均垂向速度分布。当s/D=2.5时,第1孔射流与第2孔射流主体汇合较早,当z/D>5.0时,其流动特性与波流环境中单孔射流较为相似;当s/D=5.0时,第1孔射流的一部分脱离出射流主体,成为“污染物云团”并与第2孔射流左侧分支直接接触,在z/D=17.0高度处,双孔射流的“污染物云团”之间也直接产生了相互作用;当s/D=7.0时,一大一小2个“污染物云团”从双孔射流主体上脱离,其中从第2孔射流脱离射流主体的右侧分支与第2孔射流的左侧分支产生一定程度的相互作用,此时双孔射流均与环境水体有比较大的接触面积;当s/D=10.0时,从双孔射流右侧发展而来的2个“污染物云团”尺度差异比较明显,双孔射流比较充分地暴露在环境流场中,双孔射流之间只发生了少许相互作用。由此可见,孔间距的改变会对双孔射流的形态产生影响,从直接相互作用的角度来看,孔间距的增大推迟了双孔射流的汇合,从间接相互作用的角度来看,孔间距的增大削弱了前方射流对后方射流的遮掩作用,同样也削弱了后方射流对前方射流的阻挡作用。

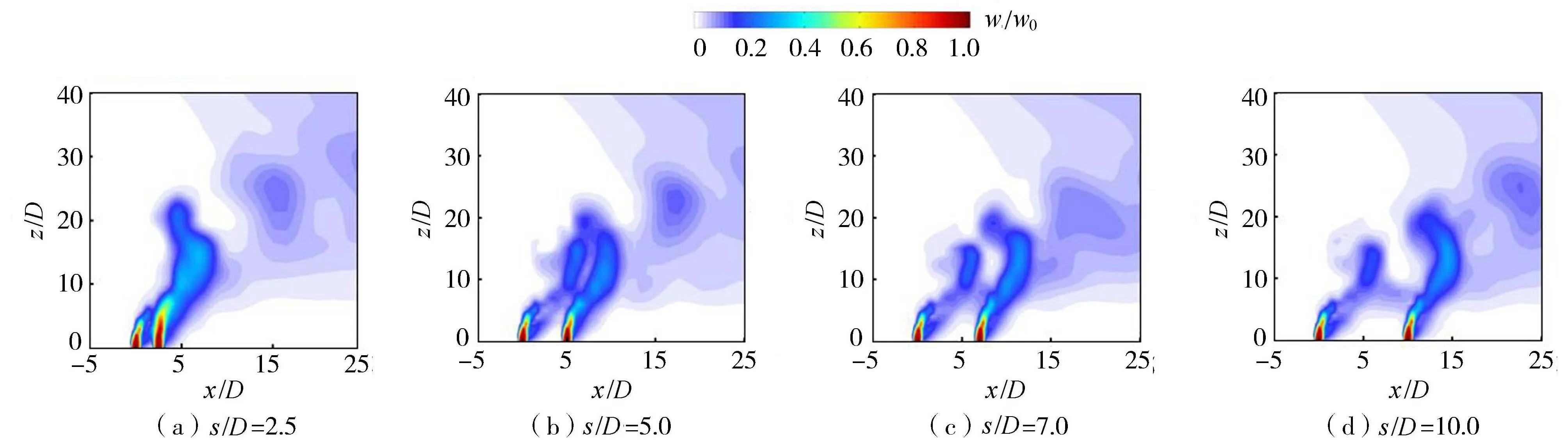
图12 波峰相位下双孔射流平均垂向速度分布Fig.12 Average vertical velocity distribution of double-hole jet under wave crest phase

图13为不同相对孔间距垂向速度沿主轴线的衰减曲线,可以定量分析射流间相互作用对其运动扩散特性的影响。从第1孔和第2孔的速度衰减曲线中发现,孔间距与扩散效果并非正相关,射流与射流之间的相互作用也会加速扩散过程。当s/D=7.0时,垂向速度衰减最快,双孔射流运动扩散效果最佳。

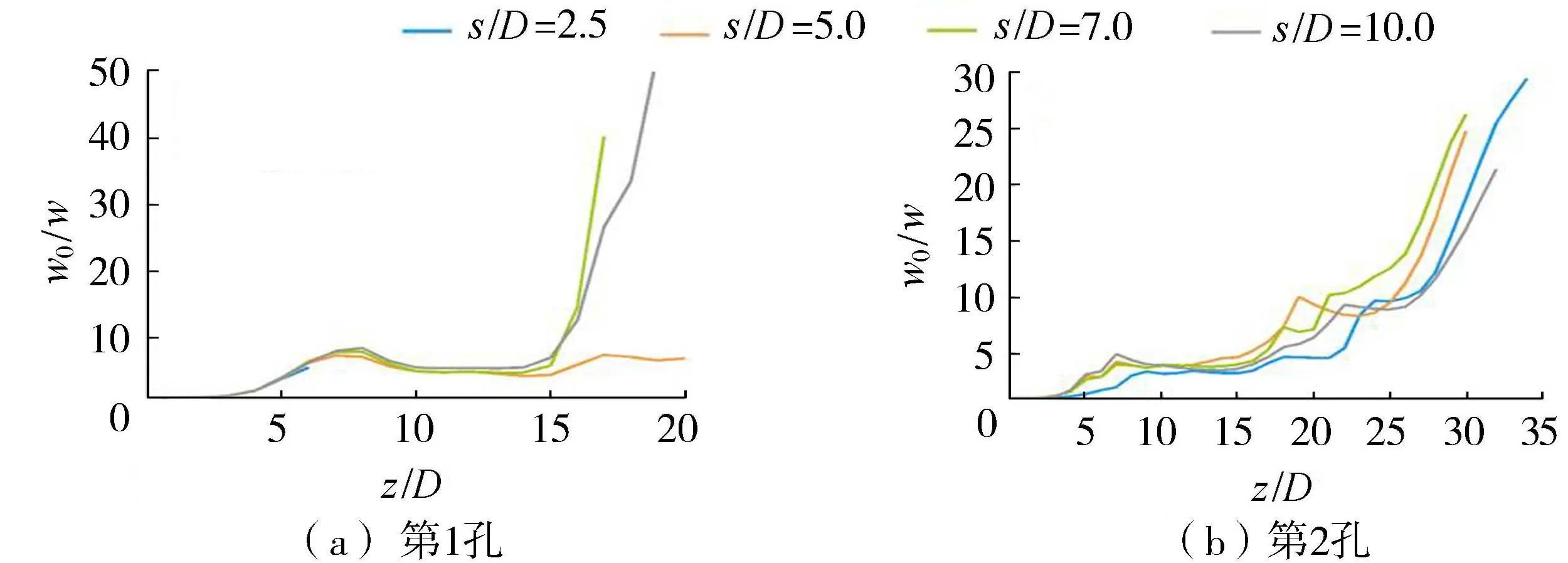
图13 双孔射流垂向速度沿主轴线的衰减曲线Fig.13 Attenuation curve of vertical velocity of double-hole jet along the main axis

综上可知,射流与环境水体、射流与射流之间的相互作用都能够加速射流运动扩散过程。随着孔间距的增大,双孔射流之间的相互作用慢慢削弱,而射流与环境水体之间的相互作用却在慢慢增强,在本文试验组次设置下,s/D=7.0为最优相对孔间距,在此设置下,出现了双孔射流之间、射流与环境流体之间同时发生较充分掺混的情况。

3 结 论

a.在波谷相位时刻,由于横流与波浪相互作用强烈,流场内的三维涡旋结构丰富、尺度较大、数目众多,有利于射流与环境水体、射流与射流之间的掺混,这是波流环境比单一横流环境中多孔射流运动扩散效果更佳的主要原因。

b.波浪强度越大,射流轴线速度衰减越快,稀释扩散效果越佳;波浪强度越大,弯曲平台越早出现,汇合位置更低,多孔射流更早地发生汇合。

c.孔间距的改变会对双孔射流的形态产生影响,从直接相互作用的角度来看,孔间距的增大推迟了双孔射流的汇合;从间接相互作用的角度来看,孔间距的增大削弱了前方射流对后方射流的遮掩作用,同样也削弱了后方射流对前方射流的阻挡作用。

d.随着孔间距的增大,双孔射流之间的相互作用慢慢削弱,而射流与环境水体之间的相互作用却在不断增强。在本文试验组次设置下,最优相对孔间距为7.0。