骨架颗粒组成对散粒土管涌规律影响的试验研究

梁 越,喻金桃,张 强,许 彬,张宏杰, 龚胜勇

(1.重庆交通大学国家内河航道整治工程技术研究中心,重庆 400074;2.重庆交通大学河海学院,重庆 400074; 3.内江市建设工程质量检测试验中心,四川 内江 641100)

管涌本质上是土体内部细颗粒在水流拖曳力的作用下随着水体被冲刷带走,在土体内部形成渗流通道,导致土体内部结构发生改变从而整个土体失稳、发生坍塌的现象。管涌破坏造成失事的事件约占堤防失事总量的一半,其中堤基以及堤身位置处的渗流对堤坝的破坏最严重,若不及时排除,会使堤基发生不均匀沉陷并导致崩堤的严重后果,因此堤坝渗漏的探测和修补尤为重要。仉文岗等[1-2]将高密度电阻法用于渗漏隐患探测;梁越等[3]试验研究表明,在土石坝坝面渗漏进口铺设希德拉顿颗粒材料防渗性能较好,这对开展管涌的预防治理工作具有一定的意义。但是管涌发展过程受到诸多因素的影响,具有很强的随机性、隐蔽性,且难以监测,基于此,宗梓煦等[4-5]将透明土引入到管涌侵蚀研究中,为管涌侵蚀可视化研究提供了方向,但其治理依然具有相当大的难度。

国内外学者利用室内试验和数值模拟等方法对管涌问题进行了广泛深入的研究。沙金煊[6]通过计算临界细颗粒含量来判断渗透破坏类型,此外还可采用颗粒级配曲线判别法[7]、不均匀系数判别法、细颗粒含量法[8]等来判断渗透破坏类型。Liang等[9-12]分别采用室内渗透破坏试验和数值模拟等方法建立了临界水力梯度公式,并通过与试验结果的比较验证了公式的准确性。倪小东等[13]为研究管涌的细观机理,开展了不同颗粒级配、细料含量等方面管涌的数值模拟,揭示了不同因素条件下对管涌发生发展的影响。Nguyen等[14]通过数值方法研究了土体孔隙度、颗粒均匀性等对内部侵蚀和水力临界状态的影响。常东升等[15-18]从水力条件(渗流方向、水头形式等)出发,结合物理条件(孔隙率或者孔隙比、密实度等)和几何条件(粒径比、颗粒级配等),对管涌问题做了大量的研究。陈亮等[19-20]通过管涌试验以及管涌后的排水剪切试验,分析了3种不同细颗粒含量对临界水力梯度、累积涌砂总量、涌砂速率的影响,在此基础上,以常水头下管涌规律作为对照,得到变水头下土体内部细颗粒运动及迁出规律。张改玲等[21-22]研究了不同应力、不同水力梯度条件下土料渗透系数随围压、应力水平等因素的变化规律,建立了土体渗透系数的经验公式。贺林林等[23]从不同砂土颗粒排列角度入手,揭示了不同砂土颗粒排列角度对砂土剪切特性的影响规律。

目前不同细颗粒含量对管涌规律的影响研究已取得了大量的成果,但对不同骨架颗粒含量的研究较少。本文采用自制渗透试验系统进行管涌试验,通过在不同骨架颗粒含量条件下试样发生管涌时的临界水力梯度、渗流速度、细颗粒流失量等数据来分析骨架颗粒1～2、2～3、3～5mm 3个粒径段对管涌规律的影响。

1 散粒土管涌试验

1.1 试验材料

采用石英砂散粒土配制不同间断级配试样,骨架颗粒粒径2～10mm,细颗粒粒径为0.075～0.25mm,主要研究1～5mm粒径段颗粒组成含量(质量分数,下同)不同对试样的渗透破坏影响。按照不同粒径段颗粒含量,配制J1～J5共5组试样,其细颗粒含量均为20%,各粒径段颗粒如图1所示,骨架颗粒级配曲线如图2所示。

图1 各粒径段颗粒Fig.1 Particles of each particle size range

图2 骨架颗粒级配曲线Fig.2 Particle size distribution curve of skeleton

1.2 试验装置

试验采用自行研制的渗流试验系统,主要由供水系统(调节上游水位)、轴压施加系统、装样室和砂水分离收集系统组成,如图3所示。上游恒定水位水箱为可升降的供水箱,水箱内分别连接3支水管,由下而上依次为入水管、出水管与泄流水管。入水管与自来水管连接向水箱注水,出水管向试样提供恒定的水位,泄流水管则可以排出水箱内多余水量。

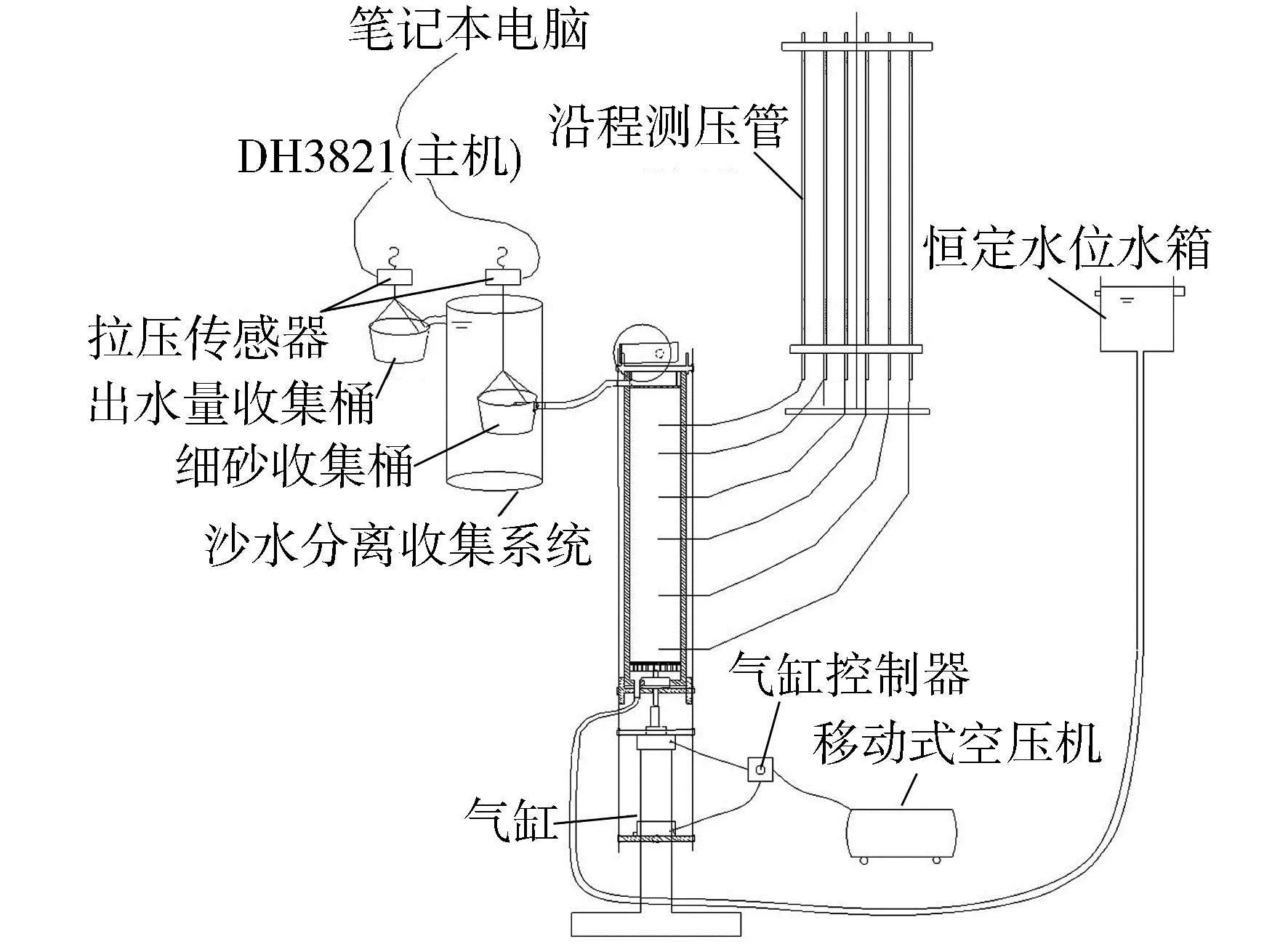
图3 试验系统示意图Fig.3 Schematic diagram of test system

轴压施加系统主要由移动式空压机、气缸以及气缸控制器组成。钢板通过连接气缸的活塞杆向装样室底部施加轴向压力。通过调节空压机调节阀向气缸输出稳定的空气压力,再由气缸向试样提供恒定的轴向压力。

装样室由PMMA管制成,管径10cm,管厚1cm,管长50cm,试验前完整土样长32cm,由装样室底部的钢板支撑,该钢板厚度为0.5cm,散布着间隔为6mm、直径为5mm的圆孔,这些圆孔在试验中为装样室底部提供均匀的水流,为防止细颗粒脱落,钢板上带有一个75μm孔径的钢丝筛。装样室顶部的网格可以防止粗颗粒的流失,但允许水和被侵蚀的细颗粒通过。

砂水分离收集系统主要由数据采集器DH3821、拉压传感器、细砂收集桶和出水量收集桶组成。细砂收集桶底部由孔径小于细砂粒径的纱网构成,当挟砂水流通过管道流入收集桶后,细砂在重力作用下落在细砂收集桶内,多余的水量则通过上部泄水管流出。拉压传感器用来测量细砂累积量与渗流流量。为了有效防止细砂向四周飘散,对涌出细颗粒的收集过程在水下完成。数据采集器记录试验过程中的数据,包括传感器检测到的涌出细砂的质量、装样室两端的水头、施加于试样底部的应力以及试样的变形。

1.3 试验步骤

为得到3个粒径段骨架颗粒对管涌的影响规律,将5组试样分为3组试验,试样J1、J2和J3为A组试验,试样J1与J4为B组试验,试样J3与J5为C组试验。试验发现试样干密度为1.92g/cm3时,在高低两种轴压应力作用下试样不会发生能够影响整体渗透系数的变形,初始变形仅在2cm以下。因此将3组试验试样干密度均设置为1.92g/cm3,渗流方向均为竖直向上,轴向压力均控制在80kPa。具体试验步骤如下:

a.按照5组试样的颗粒级配将不同范围粒径的土料进行拌和,然后掺入4%干土质量的水至接近最优含水率[24],搅拌均匀,利用欠压实法[25]将混合均匀的土样分成16层装填,每层厚度为2cm。

b.将气缸调为垂直方向,连接试验系统。

c.打开数据采集器,并标定传感器。

d.保持上游水位略高于下游水位,通过逐渐抬高上游水箱直至水位达到试样顶部,静置4h让试样饱和。

e.观察并确定试样内无气泡之后,调节空压机,给试样施加预设轴压至80kPa。

f.抬高上游水箱,初始阶段以0.2cm/min的速度缓慢抬升上游水头,后期以0.1cm/min的速度抬升上游水头直至获得临界水力梯度后保持稳定。通过质量传感器采集涌砂量以及渗流流量。

2 试验结果与分析

2.1 试验现象

土体颗粒级配直接影响渗透破坏发展的可能性、发展速度以及最终发展状态,是管涌发展过程的主要影响因素。试验中5组试样均为竖直向上渗流,在相同的轴向压力条件下均发生渗流破坏现象。5组试样在渗透破坏前,均未发生较大的轴向压缩变形,轴向压缩变形仅为1mm左右,随着水力梯度的上升,试样内部有细颗粒开始在渗透力作用下向上移动,试样内部局部出现较小的坍塌,并伴随着细颗粒的涌出,直至试样破坏,试样J2在后期发生较大的轴向压缩变形。

2.2 渗流速度和临界水力梯度

图4为试样水力梯度与渗流速度关系曲线。试样在水力梯度较小时,渗流速度均与水力梯度呈线性关系,基本符合达西定律,而随着水力梯度的上升,每组试样渗流速度的变化各有不同。

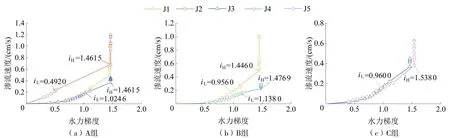
图4 不同试样渗流速度随水力梯度变化曲线Fig.4 Variation curve of seepage velocity with hydraulic gradient in different samples

A组试验试样的差别在于2～3mm与3～5mm粒径段颗粒相对含量不同。J1与J3两组试样渗流速度随水力梯度变化关系一致,初始渗透系数(图中斜率)分别为0.12、0.11cm/s,J1曲线斜率更大(图4(a)),而试样J2的初始渗透系数为0.4cm/s,远大于前两组。

B组试验试样颗粒含量组成区别在于J1试样不含1～2mm粒径段颗粒,J4试样不含2～3mm粒径段颗粒,其余颗粒组成相同。从图4(b)可得J1和J4试样初始渗透系数分别为0.12、0.08cm/s。C组试样的差异在于J5试样含有1～5mm粒径段颗粒,而J3试样不含有1～2mm粒径段颗粒,从图4(c)可以看出C组试样的初始渗透系数基本一致,但后续管涌发展过程中,J5试样的渗流速度小于J3试样。

将试样内部细颗粒出现局部性运动时对应的水力梯度作为下限临界水力梯度(iL),而将试样细颗粒达到稳定出流出现整体运动时对应的水力梯度作为上限临界水力梯度(iH)[26],相应的临界水力梯度值及位置如图4所示。

根据骨架颗粒级配曲线,可确定出5组试样的特征粒径d10、d30、d60(在骨架颗粒中分别占10%、30%、60%的粒径),由此可算出骨架颗粒不均匀系数(Cu)和曲率系数(Cc)。如表1所示,5组试样的上限临界水力梯度均在1.5左右,而下限临界水力梯度有一定差距,说明骨架颗粒组成的不同对细颗粒起动条件有着较大影响,而对试样发生渗透破坏临界条件影响不大,且J1～J4试样的下限临界水力梯度与骨架颗粒不均匀系数基本成正比关系。因为不均匀系数大于5且曲率系数等于1～3代表级配良好,5组试样的不均匀系数均小于5,且曲率系数均在1左右,所以不均匀系数越接近5,即越大,代表级配越良好。从表1可以看出,J4试样的下限临界水力梯度最高,不均匀系数和曲率系数均为最大,在5组试样中级配最好,故发生管涌的时间最晚,细颗粒最不易起动。J2试样的下限临界水力梯度最低,不均匀系数最小,故发生管涌的时间最早。总的来说,J1～J4试样的下限临界水力梯度随着骨架颗粒不均匀系数的增大而增大。J5试样由于有1～3mm粒径段颗粒的堵塞作用,下限临界水力梯度为0.96,相比完全不含1～2mm粒径段颗粒的J1与J2试样来说,下限临界水力梯度更高,细颗粒更不容易起动;但J5与J3试样相比,J3试样虽不含1～2mm粒径段颗粒,但有足够含量的2～3mm粒径段颗粒,所以两者的下限临界水力梯度相当。

表1 试样骨架颗粒级配特征及临界水力梯度Table 1 Gradation characteristics of skeleton particles and critical hydraulic gradient for soil sample

2.3 累积涌砂量和涌砂速率

通过砂水分离收集系统实时收集涌出的细颗粒,采用以下公式可以计算出试样管涌过程中的累积涌砂干质量:

ms=mbγs/(γs-γw)

(1)

式中:ms为累积涌砂干质量;mb为累积涌砂浮质量;γs为土颗粒容重;γw为水容重。

A组试验3组试样2～3mm粒径段含量与3～5mm粒径段颗粒含量比值分别为1∶1、1∶2、2∶1,对比其累积涌砂量随时间变化曲线(图5(a))可以发现,随着2～3mm粒径段颗粒含量的增加,累积涌砂量呈现减少趋势,J2试样累积涌砂量约752g,占细颗粒总量的77.3%。而J3试样累积涌砂量则仅为515g,占细颗粒总量的52.9%。从图5 (b)可以发现,两者的累积涌砂量差异逐渐增大,J1试样累积涌砂量约为420g,占细颗粒总量的43%,而J4累积涌砂量仅为115g,占细颗粒总量的11.8%,两者累积涌砂量差异较大(305g)。如图5 (c)所示,C组试验试样的管涌发展程度很接近,在80min以后开始出现较小的差异,J5试样在100min后管涌发展趋于稳定,最终累积涌砂量保持在414g左右,约占细颗粒总量的42.5%。同一时期,J3试样累积涌砂量仍在缓慢增加,管涌发展到233min时J3累积涌砂量从463g较快增加至506g,此时发生了约8mm的轴向渗透破坏变形,出现了陡增现象,最终稳定在530g。

图5 累积涌砂量随时间变化曲线Fig.5 Variation curve of cumulative sand gushing with time

为进一步研究土体颗粒级配对管涌发展规律的影响,根据试验结果制作出涌砂速率随时间变化的散点关系图,并拟合5组试样的涌砂速率随时间变化关系曲线,结果如图6所示。A、B、C 3组试验试样的涌砂速率随时间变化关系曲线均有降低且逐渐趋于零的趋势。从图6(b)可以看出,J1试样在试验前50min平均涌砂速率稳定在8g/min,而J4试样平均涌砂速率稳定在5g/min,要远小于J1。与此同时,J1试样涌砂速率的峰值能达到32g/min,也远大于J4的12g/min。J4试样整体管涌发展过程较为平缓,涌砂速率波动较小,J1试样整个管涌发展过程有明显的变缓趋势,涌砂速率从32g/min降低至后期的1.7g/min,波动性较大。如图6(c)所示,J5试样在管涌整体发展过程中涌砂速率较为平缓,峰值不超过3g/min,而J3试样的涌砂速率波动性较大,峰值可达20g/min,远大于J5。

图6 涌砂速率随时间变化曲线Fig.6 Variation curve of sand gushing rate with time

3 讨 论

在发生渗流时,细颗粒乃至骨架中较细颗粒会随着渗流涌出,较粗颗粒之间的孔隙没有粒径较小的骨架颗粒去填充,容易形成稳定的渗流通道,且试样的较细颗粒含量越小,其初始渗透系数以及累积涌砂量就会越大。对比J1、J2和J3这3组试样发现,2～3mm粒径段颗粒分别占了骨架颗粒的18.75%、12.5%、25%,3～5mm粒径段颗粒分别占了骨架颗粒的18.75%、25%、12.5%,而这3组试样的初始渗透系数(图4(a)中曲线斜率)分别为0.12、0.4、0.11。相较于J2组试样,J1和J3组试样的渗透系数相差不大,这可能是因为J1和J3组试样2～3mm与3～5mm粒径段含量差距不大,反观J2组试样,其2～3mm粒径段颗粒比其余两组少得多,但其3～5mm粒径段颗粒又更多,所以其渗透系数会更大,这说明了2～3mm粒径段对于降低渗透系数效果要比3～5mm粒径段更好,这一结论也可以从图5(a)中的累积涌砂量与涌砂时间关系得到证明,从图4(b)(c)和图5(b)(c)也能得到佐证。

4 结 论

a.不同颗粒级配的试样,在管涌发生前,水力梯度与渗流速度呈线性关系,基本符合达西定律。

b.骨架颗粒组成的不同对细颗粒起动条件有着较大影响,而对试样发生渗透破坏临界条件影响不大。完全不含1～2mm或2～3mm粒径段颗粒的试样,其下限临界水力梯度与骨架颗粒不均匀系数基本成正比关系。

c.骨架颗粒组成的不同对管涌发展过程也有较大的影响,其中1～2mm粒径段颗粒的堵塞作用最强,相比完全不含1～2mm粒径段颗粒的试样,细颗粒最不易起动;2～3mm粒径段颗粒的堵塞作用要强于3～5mm粒径段颗粒,在无1～2mm粒径段颗粒的情况下,2～3mm粒径段颗粒相对更多的试样,细颗粒更不易起动。

本文试验仅设置了1组同时含有1～2mm、2～3mm和3～5mm 3种粒径段的试样,且其骨架颗粒不均匀系数与下限临界水力梯度的变化规律和其余4组试样不一致,因此本文试验试样组成上缺少多样性,故在不同骨架颗粒级配对管涌发生规律影响的讨论上存在局限性,需要进行更深入的研究。