一种基于K-means 的神经网络数据集回归预测算法
孙梦觉,田 园,汤 吕,李 珗
(1.云南电网有限责任公司信息中心,昆明 650000;2.昆明云电同方有限责任公司,昆明 650000)
电网智能化处理用户数据的相关应用正在国内快速发展,基于电网数据的回归分析和分类模型的相关研究已趋于成熟化。但常用的电网数据分类算法是基于经典统计学算法,导致分类模型中,模型结果更多的是偏向电网用户中的数据离群样本,因此影响了整体预测分析的精确度。同时,常见的统计学算法在面对不止含有单一维度数据的多维数据时,不能有效提取并处理多维数据集的样本特征,因此,为了解决上述此类问题,国内外的研究者们提出了许多基于机器学习的回归和分类算法[1]。例如,Xiao 等[2]提出了非均衡数据集分类算法,通过评估参数筛选出数据集中少数类样本的特征属性,从而实现优化分类器精确度的目的。而张明等[3]提出了采用混合采样的分类算法,通过对少数类在稀疏域使用过采样方法,多数类在密集域使用欠采样方法,然后对二者平衡后的数据集使用由决策树组成的分类器进行分类,从而得出更加精确的分类结果。陶新民等[4]则是将逐级优化递减欠采样和边界人工少数类过采样算法进行有效结合。首先,对样本类进行降采样,然后选择边界样本进行升采样,该步骤的目的在于去除噪声的干扰,从而保留有效的数据。Moayedikia 等[5]则提出了高维数据特征选择分类算法,在高维非均衡数据集中衡量分类标签相关特征下,通过选取相关度最高的一组使分类效果达到最佳。接着,Ando 等[6]提出一种深度过采样框架下非均衡数据分类算法,通过深度特征模型对少数类进行重采样,从而有效地改善数据类别之间的不平衡性。但是,分类模型并不适应于一些极端不平衡的数据样本,因此,如何对数据集中最具有特征的样本进行挖掘,成为了特征工程中一个代表性问题,对此研究者们提出了一些更优异的算法。例如,Chung 等[7]将代价敏感策略引入深度学习的分类算法中,通过在深度学习模型的损失函数中加入代价因子,从而减少了对样本的错误分类。Ng 等[8]则提出了双重自动编码器的非均衡数据分类算法,由2 种激活函数分别计算得到对应的自编码网络,实现数据集中多数类和少数类样本的学习训练,提取分类特征。随后,Khan 等[9]提出了基于数据特征学习的分类算法,通过优化卷积神经网络(Convolutional Neural Network,CNN)模型中的特征学习过程,使数据特征对数据集分类具有了更高的判别性。Douzas 等[10]提出了基于生成对抗网络的非均衡数据分类算法,生成对抗网络训练出少数类样本,通过这样的少数类样本让深度学习分类器模型得到分类的特征表达,从而去改善数据集中少数类样本的识别率。张文东等[11]提出了基于改进反向传播(Back Propagation,BP)神经网络的非均衡分类算法,通过在模型隐含层之间加入一种特征损失层,即可去除冗余的数据特征,降低数据集的非均衡性。
上述列举的研究成果对于电网小样本数据集的分类结果有明显改善,但对于大数样本则效果一般。文献[12]中指出,在数据分类处理过程中多维数据特征选择存在信息丢失,类别之间错分代价不同,导致分类结果鲁棒性较差。而文献[13]研究说明神经网络能够不断地训练特征响应,从而得到表达能力强的抽象特征,在抽象特征中提取数据特征后保留有效信息,上述二者研究证明了神经网络相关方法在多维数据特征工程领域的优越性。
而本文对多维度样本数据集回归分析是结合文献[14]中提出的分类和回归相融合的方法,首先将数据集样本采用K-means 分类器算法进行特征维度抽象并聚类,得到数据特征集合,在数据集合中,遴选聚类中心进行迭代划分,之后按照划分结果计算RNN 神经网络模型中隐含层的权重系数,根据训练好的分类器通过样本数据输出相应分区的聚类结果,从而获取分区后的样本特征点。通过K-means 方法将多维数据降维到二维数据并求取其聚类超参数,从而构建RNN 神经网络迭代特征学习模型。本文在一定程度上平滑多维数据样本中少数样本离群点对整体模型精确度的影响,提高整体回归分析模型的准确性,以求改善大数据集的分类结果。
1 RNN 神经网络算法
RNN 神经网络的学习训练由网络输入层和前向输入层序列数据的记忆网络共同组成[15-16]。首先在输入层中,假设在N个数据样本的集合中,数据集合序列{(xi,yi)|x∈Rm,y∈Rn,i=1,2,…,N} 为离散时间序列,Rm表示输入层有m个神经元,Rn表示输出层有n个神经元。RNN 神经网络完成了训练样本从输入到输出的高维非线性映射f:Rm→Rn,再由检测样本来检验网络的泛化能力。该过程的映射关系表示为
式中:wij表示记忆网络的权重系数;ηj表示在输入层中,此刻输入层网络神经元的权重数据;zjt表示在隐含层中,隐含层网络的权重系数;rt表示在隐含层中,加入的偏置参量;xi(t-1)表示t-1 时刻的网络数据;xi(t)表示t时刻的网络数据。在第t=1 个时刻会进行网络的初始化。其中f[*]和xi(t)中包含了激活函数,文章中f[*]激活函数采用了sigmoid 函数,xi(t)则采用了softmax函数。
鉴于网络在一次迭代过程中,无法得到准确的输出结果。因此,需要依靠时间反向传播(Back-propagation Through Time,BPTT)的过程,将误差信号从输出层流入各中间层,逐层不断修改隐含层的神经元权重值。在网络的迭代过程中,网络本身的全局误差会不断向最优值趋近,以此优化算法分类的有效性。其中隐含层权值的变化为
通过累计误差方法去不断调整RNN 算法网络中记忆网络的权值wij,使全局误差E进一步优化,即
式中:λ 为网络的学习率,对于p个输入的数据样本,采用x1,x2,…,xp来表示,第p个样本输入到RNN 神经网络后得到输出ypk,通过平方型误差函数或者交叉熵损失函数得到第p个样本的误差Ep
式中:tpk为p数据样本在第k个输出层的期望输出。神经网络算法结构图如图1 所示。
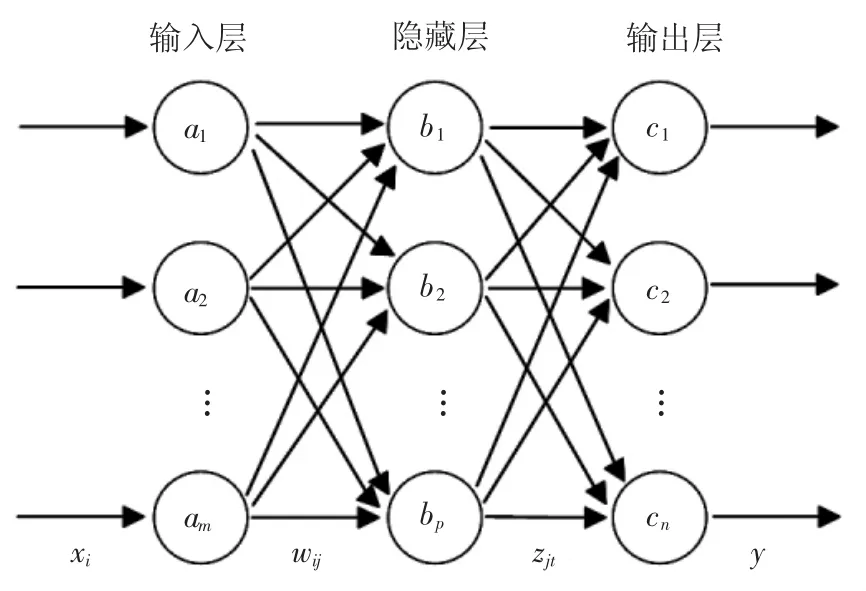
图1 神经网络算法结构图
2 K-means 的RNN 神经网络趋势预测模型
当前,常见的回归算法是通过特征选择、降维[17-18]等数据预处理过程减少迭代过程中产生的经验误差,但该过程降低了数据内部的有效特征信息量,影响了后续组合模型的性能。
本文算法首先根据训练样本建立RNN 多层神经网络初始化模型,再使用K-means 方法管理RNN 神经网络的输入层,计算多个输入层数据的维度属性价值量用来调整权重参数,使输出层得到隐含层中迭代加权后的最佳响应值。然后,以最佳响应值对应的样本聚类特征点计算同类样本中最大信息维度,在输出层神经元构建含有数据特征信息的预测模型。最后,在组合模型的输出层调整样本集遍历后的数据测试结果,对照测试集并通过MSE和MAE函数来验证准确率。
2.1 K-means 聚类模型的构建
本文首先通过聚类方法对输入层的多维数据进行权重融合,在数据维度信息价值分布不平衡时,有效地处理多维度数据。从而避免了类间信息价值差异大的部分样本出现影响预测结果的问题。然后,使用K-means聚类方法中平滑更新的方式来保持模型可靠性。由于神经网络共享了多个隐含层中的所有参数,因此节省了存储空间并避免了网络冗余。最后通过判断最大响应值来对少数类样本分类,避免了数据的过拟合[19-20]。
根据K-means 分类器方法把二维数据的结构抽象为T={V,S},T集合中S和V 参数表示维度特征,νi,Sk之间的距离表示2 个特征之间的关系,则T集合中的特征关系通过欧拉公式的长度定义为
式中:T集合中用来训练数据点样本集合,k表示数据集合中的聚类个数,分类的特征结果由模型分类器输入,φu(*)表示特征数据在二维空间上的分布,根据数据中的不同聚类中心划分聚类边界,计算聚类模型的分布函数H(νi,sk)
式中:zjt为特征数据在第t次迭代上的权重系数,本文通过少数类的可靠度自适应函数得到权重值,公式(2)修改为
式中:ανt表示数据点中隐含层分数的最大值,但忽略了可靠性问题,如果分类区间划分不佳,则会对后续预测结果造成很大的影响,所以需要沿着迭代过程更新超参数,计算各聚类结果的可靠度,其中每次迭代的可靠度用βν表示,公式如下
2.2 改进的RNN 神经网络模型
本文改进的神经网络算法将2.1 节得到训练样本集合中的最大响应值对应的数据点,作为代表性较强的样本特征点,然后在输出层构建回归预测模型。本文提取序列特征再进行K-means 聚类计算,得到了数据样本特征集合。该过程是算法中区分特征显著性的关键步骤[21-23]。
假设训练样本响应后集合为:Φ={(xi,yi),1≤i≤c},其中c为训练后数据样本的类别数,xi为第i类的训练样本特征点,yi为其输出的参数,τi为第i类样本的特征点总数。
其中正数ri为样本特征点xi到异类样本的欧式距离,然后定义一个以xi为中心ri为半径的区域,显然在半径以外的数据点对RNN 网络迭代几乎没有影响,而半径内有较多相同类别的样本特征点。此外依照数据样本中特征最显著的样本,以此构建网络中神经元的数量,如式(9)
式中:Φ(x1,x2,…,xn)为输入的数据集合,θ 为网络中用于数据平滑的阈值,f(*)为神经元中的激励函数,通过RNN网络中神经元的运算规则可以得到对应的低维数据超平面方程
式中:wi为输出层神经元的权值,而表示为数据样本集中第i个数据点离超平面的距离,当该点位于此超平面内,则数据输出为0,否则为1。因此,对于高维数据的处理神经网络神经元的数学模型可以表示为
该神经元相当于在样本集中以核心W=(w1,w2,…,wn)为球心,以θ 为半径作一个超球面,当数据点在此球面内则输出为0,否则为1。
根据最优化K-means 聚类值构建的RNN 网络的数据回归分析模型,避免了模型向少数特异类样本的倾斜。然而RNN 神经网络输出层的分析结果,是经过相对多数遴选生成,没有考虑样本上的泛化误差。因此本文对RNN网络输出层进行必要的调整,来提高整体模型的性能。
数据分类任务是利用N个神经网络组成的集合,对参数f:Rm→Rn进行近似,其中参数Rn为网络输出,假设N个样本的期望输出为D=[d1,d2,…,dN],其中dj为第j个样本的期望输出,第i个神经网络的实际输出为fi=[fi1,fi2,…,fiN],其中fiN表示第i个神经网络在第N个样本上的实际输出。于是通过D和fi可知,第i个神经网络在这N个样本上泛化误差为
式中,对于误差公式定义为
若集成在第j个样本上的实际输出为,则集成在N个样本上的泛化误差为
根据泛化误差调整输出层的预测结果,能有效提高预测模型的准确性。
2.3 算法流程
Step1:根据公式(5)构建K-means 聚类的输入层边界。
Step2:计算数据样本的迭代模式,自适应各次迭代的权重值,建立训练迭代后的聚类应的特征点xi,确定其分类,得到最优化聚类的输出结果。
Step4:直到对剩余数据点寻找到同类的聚类区间,最后聚类结果的聚类中心对应于本文算法分类器中输入层的神经元权重结果。
Step5:对输出层计算样本的泛化误差,调整回归分析结果输出。算法流程图如图2 所示。

图2 算法流程图
3 实验结果
3.1 评价指标
损失函数定义为评价预测结果与测量值的误差指标,本文指标依照文献[24-25],取MSE和MAE为模型预测和测量值偏差的指标,准确率评价指标MSE和MAE表示为
式中:MSE当测试集和比较集的预测准确率都很高时,MSE的评价值较小。MAE的值较低时表示回归预测模型的精确值比较高,算法的可靠性较好。
3.2 UCI 回归分析数据集
表1 列举了本文在UCI 数据集上选取的3 个摩洛哥得土安市(Tetuan,Morocco)耗电量部分数据集,将数据划分为80%训练集和20%测试集,本文算法以神经网络模型作为组合模型,根据MSE值与MAE值2 种不同的Loss 函数评价指标进行比较,实验表明本文算法对电网用户数据集进行短期预测具有良好的可靠性。本文设置的实验配置处理器为IntelRi7-6700 2.60 GHz,内存为16 GB。采用TensorFlow2.1 框架实现。接下来通过实验结果对4 种不同的算法进行实验分析。

表1 实验数据集
3.3 实验分析
本文提出的基于聚类方法改进的神经网络回归算法与SVM 算法、基于统计学算法的AR 算法、基于BP改进的RNN 算法、基于时间序列的LSTM 和GRU 算法进行归一化实验对比分析。实验结果表明,本文提出的模型回归分析预测结果表现最佳,表2 和表3 为各算法的MSE值和MAE值对比结果,此外在图3 和图4 中展现了本文提出算法与真值的预测对比图。

表2 不同算法的MSE 值对比结果
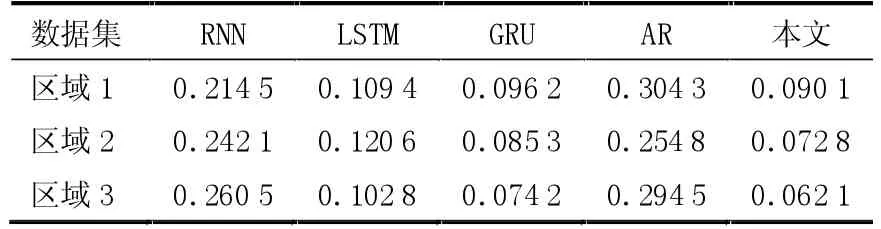
表3 不同算法的MAE 值对比结果

图3 部分预测结果图
从表2 和表3 的摩洛哥得土安电网(Tetuan,Morocco)数据集对比中,可以看出本文算法的MSE和MAE值相比其他算法得到明显优化,主要是因为其他算法,在多维数据计算中因离群类的混杂过拟合,导致查准率较低,而本文通过K-means 方法改进的RNN神经网络模型输出,由聚类特征来对样本分类进行训练归并后得出更合理的预测结果,避免了数据的过拟合,提高了预测的准确率。多维数据中存在的稀疏样本数据点会影响整体模型的预测性能,导致其他算法预测结果较差,而本文是针对样本维度特征点去计算同类样本中的聚类区间,并依照各自聚类区间训练,构建出合理的神经网络预测模型。从不同区域的样本数据集上,可以得出本文提出的改进算法在不同数据集中的数据分析效果同样较优的结论。
4 结束语
由于传统回归模型对非单一维度数据集进行回归分析时,少数奇异样本具有较高的影响代价,导致回归分析预测的准确率较低,因此,本文提出了一种基于K-means 的神经网络数据集的回归预测算法,即通过K-means 聚类算法结构优化RNN 神经网络的输入层,依照该聚类模型对应的样本特征点计算出同类样本中的最优化响应后,构建含有数据特征信息的聚类边界,再对高维数据类别进行划分从而平滑多维数据类别间因奇异值误差造成的拟合代价,提高数据集样本的预测可靠性。最后通过对比验证结果表明,在回归分析数据集中本文算法性能更优秀,超过了常见的回归预测算法,具有一定的现实意义和实操性。但本文算法并没有考虑到动态环境下,数据集中少数类样本的分布变化,下一步的研究方向是在半监督学习框架下学习训练有价值的标签数据,提高聚类算法的鲁棒性。

