基于自抗扰控制策略的直接转矩风力发电系统研究

高 宇，张继勇

（扬州大学，江苏 扬州 225100）

风能作为一种可再生能源，其广泛开发利用能够直接降低工业生产生活对于煤、石油等资源的依赖，解决来自化石能源的碳排放问题[1]。风力发电作为风能转化的有效途径，从20 世纪就开始进行研究，根据磁电能量的相互转化，将电机应用于风能到电能的改变已成为一种合理的途径。永磁直驱风力发电系统作为当前风力发电的主流机型，由于结构简单，控制效率较高受到各大厂家和学者的追捧[2-3]，在实际应用过程也因为其众多的优势助力能源市场发展得更加高效可靠。随着电机控制算法的深入研究，电机控制中相关研究成果也逐步应用于风力发电系统，基于矢量控制原理的电机控制结构也发展得十分成熟，直接转矩作为矢量控制的衍生，因结构相对简单、调速性能好、控制参数少，且对于转矩脉动等谐波抑制较为优良，但该控制策略与现有的电机控制结合仍然较为稀少，在风电领域也亟需进一步推广应用[4-6]。一些先进的现代控制理论研究更是可以和风电相结合，将风力发电系统的性能进一步提升[7-10]，提高电能产生的质量和稳定性，以适应各种工况下的不同需求。

1 风力机系统

永磁式直驱风力发电系统主要由以下几个结构组成：风力机系统、机侧变流器系统、网侧变流器系统，以及永磁同步发电机、直驱系统风力机和发电机同轴，利用风力带动发电机转动，机侧整流器将最大功率跟踪控制方法与电机常用的直接转矩等控制结合，使得发电机转速始终跟踪最佳叶尖速比下的参考转速，完成对风能的有效利用。网侧逆变器采用同样双环控制，一方面保持直流母线电压的稳定，另一方面维持系统功率因数在1 附近，使得电能能够安全合理地并入电网。

风力机是连接外界的自然风和系统装置内部永磁同步发电机的重要桥梁，构成的风力发电系统内部存在着重要的电能变换过程。风力机充分利用风资源将其转化成机械能，结合PMSG 输出最终所需的电能。整个过程和多种学科理论都具有关联性，尤其是空气动力学相关知识。根据相关原理，风机的转速和风速之间的关系为

式中：λ 为叶尖速比，通常存在一个最优值使得电机转速也同样获得最佳值；ν 为风速；R为风机叶轮的半径；ω 为风机的机械角速度。风力机利用叶片收集风能，其输出的功率Pm和转矩Tm可进一步表达为

式中：ρ 为空气密度，β 为叶片的桨距角，Cp为风能利用系数，作为风力发电系统的一个重要参数反映出系统对风能的利用率的高低，常用风轮的具体数值为

从式（3）中可以看出，风能利用系数Cp和叶尖速比、桨距角之间存在着一定的数量关系。通过改变β 或λ 的大小，进而改变Cp的大小，使得系统能够在最佳状态运行，此时风力机能够最大程度地捕获风能，提高整个系统的资源利用率和运行效率。根据式（3）在MATLAB 中建立逻辑算式，画出在不同桨距角和叶尖速比条件下，式（3）所对应的函数Cp曲线关系图，如图1 所示，在不同的桨距角条件下，风能利用系数呈现抛物线趋势，随着叶尖速增加先递增后递减，最大功率点只有一个。当桨距角为0°且叶尖速比为8 时，风力机存在最大的风能利用系数为0.45，实际仿真和设计过程便可采用该参数进行风力发电系统中风力机模型的建立。

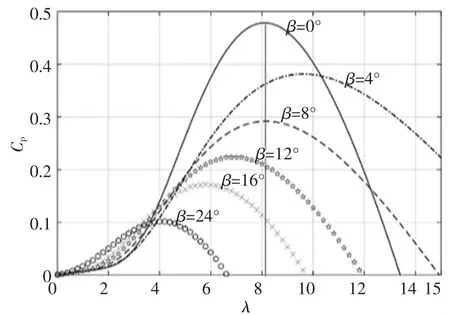
图1 风能利用系数曲线

2 永磁同步发电机系统

根据电机基本特性分析可知，永磁同步发电机在dq坐标系下的电压和磁链方程为

式中：ud、uq、id、iq、ψd、ψq为永磁同步电机在dq坐标系下的电压、电流、磁链，Rs为电机定子线圈电阻，ωe为电机永磁转子电角速度，ψf为永磁转子磁链幅值。

永磁同步发电机的运动微分方程可描述为

矢量控制系统内部最内层环节便为转矩控制环，只不过其以电流形式呈现，直接转矩控制则通过观测环节得到转矩磁链矢量，继而控制磁链和转矩转差率输出转矩，实现电子磁链的旋转。定义转子磁链和定子磁链之间的夹角为转矩角，当负载稳定不变时，转矩角随着定子磁链同步旋转，保持恒定不变，可表示为

根据坐标变换原理，对式（4）中磁链关系进行进一步改写

根据定子磁链矢量控制原理可知，ψx=ψs，ψy=0，则

系统负载转矩可进一步表示为

一般而言，常见的表贴式PMSG 定义dq轴系下的电感值相等，转矩公式可进一步化简成为

根据式（10）可知，当永磁体磁链幅值维持恒定不变时，直接转矩控制可以利用改变δ 角和ψf来实现对发电机的输出转矩Te的实时控制。为了进一步简化该公式，永磁同步发电机通常默认定子磁链也为恒定，在理想情况下，电磁转矩只和转矩角度相关，只需获取转矩角度便可实现对于永磁电机转矩的精确控制。

3 自抗扰控制策略

实际的永磁同步发电系统在实际运行过程中，不可避免地出现一些外在和内在的因素，造成发电运行过程中的抖动现象，传统的PI 控制并不能很好地消除这些干扰，为进一步提升发电系统自身的调速性能和抗干扰性能，现提出将自抗扰控制策略加入系统速度环内。自抗扰控制策略首先需要明确控制对象的基本数学模型，由式（5）可将永磁同步发电机的运动微分方程进行变形，构造成标准的一阶非线性系统，其方程可进一步表示

式中：Te表示电磁转矩，自抗扰控制讲究将系统内外所存在的干扰集合起来，d（t）为系统内外集总扰动，δ 为电机电磁转矩系数。

根据永磁同步发电机的一阶模型建立线性扩张状态观测器模型

式中：z1为x1的估计值，z2为系统总扰动x2的估计值，β1、β2为系统增益参数。

由此可得，速度环自抗扰控制器整体可表示为

式中：k1是比例系数；ωm*是期望输出。

4 仿真与分析

本文采用Matlab/Simulink 软件对所提出的直接转矩控制的发力系统策略进行分析和研究，通过对比PI和自抗扰控制下的直接转矩发电系统在随机风下的功率跟踪性能来验证该策略的可行性和抗干扰能力。表1 给出系统的仿真参数。

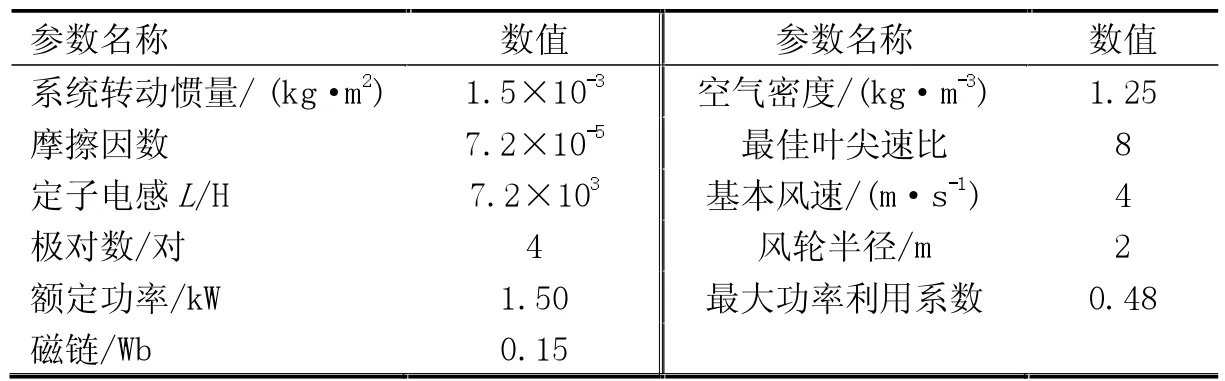
表1 风力发电仿真参数

根据该仿真参数，建立永磁直驱风力发电系统的风速模型和发电机控制基本模型，并将基本PI 控制的速度环替换成ADRC 控制，分别调节PI 和ADRC控制下的风力发电系统模型，对比二者在同一风速模型下，系统对于最大功率点下转速跟踪性能。如图2所示。

根据图2 最大功率点下的速度给定跟踪曲线所示，其中，Reference为参考输入速度曲线，PI为PI 控制下的速度跟踪曲线；ADRC为自抗扰控制策略下的速度跟踪曲线。2 种控制策略都能够根据理论计算的风速模型曲线进行总体趋势上的跟踪，PI 控制也充分展现其控制的稳定性，在风电领域也可实现控制目标。进一步分析跟踪曲线发现，本文提出的自抗扰控制策略可以更好地跟踪速度指令，超调和稳态偏移量情况明显优于PI 控制下的风力发电系统，在风速突变的情况下，自抗扰控制下的风电系统仍可跟踪给定风速曲线，不存在波动情况。

5 结束语

风力发电直接转矩控制作为风电系统一种较为新颖的控制策略，其逐步推广和应用将丰富风电控制结构。针对传统PI 控制下系统跟踪性能和抗干扰能力上的缺陷，引入自抗扰控制策略优化整体的控制结构，一方面提升系统跟踪性能，让风电系统始终能以最大功率捕获点状态运行，另一方面将系统内外扰动全部补偿，进而提升系统面对风速突变的抗干扰性能。