一种自由分布的LSTM算法在多尺度风速预测中的应用

成骁彬

(上海电气风电集团股份有限公司,上海 200241)

0 引言

考虑到石油类能源的短缺和市场日益增长的需求,近几年来我国的可再生能源,如太阳能、风能、水能、生物质能源得到了迅猛的发展。风作为最重要的绿色能源之一,在发电过程中不会产生新的碳排放。在双碳背景下,风电行业的装机容量增长极为迅速,2016年全球风电的装机总量大约在55 GW左右,而这个数字在2022年变为了487 GW。风力发电机组发电的源头来自风,其拥有不确定性和难以预测性。因此,对于风速的精准预测在风电行业起着决定性的作用,同时在“源网荷储”一体化的新型电力系统下,精准的风速预测可以有效地减少新能源对于电网的冲击。Sun等[1～4]显示结合各类LSTM模型的方法来进行短时风速预测,具有优秀的成果。长短期记忆网络(LSTM)算法是一种有记忆和遗忘机制的模型,能够有效得解决“维数爆炸”的问题。Liao等[3]使用了一种双层长短期记忆网络和注意力机制的模型(DLSTM-AT)用于多尺度的预测。Shen等[4]使用了一种卷积网络和长短期记忆网络混合算法(CNN-LSTM)用于处理风机的时空属性数据。但上述研究都没有考虑到工业化应用,尤其是在小样本数据时,对于LSTM算法在风速预测领域的精度提升,尤其是在不同尺度下的综合预测进度表现。同时,算法模型本身的退化没有得到很好的监控,使得模型在线状态属于“黑盒”状态。鉴于此,本文提出了一种自由分布LSTM算法,用于短时风速的预测。该算法利用指数分布(Exponential Distribution)和泊松分布(Poisson Distribution)的共轭属性,形成一种自由分布解决方案,同时使用概率分布指标作为迭代过程中的损失方程,能让模型更具有泛化性。该模型在多种尺度上均能保证预测精度。

1 自由分布LSTM算法

1.1 数据收集与处理

数据收集与处理包含数据收集,数据分类和数据清洗。本文数据来源于中国江苏省某4-MW风机机组,数据采集系统为30秒SCADA数据(Supervisory Control and Data Acquisition),数据采样周期为2022年6月-2022年8月。本文将数据分为训练集(1 000个观测值)和测试集(4 500个观测值)。在数据清洗过程中,本文进行了包含NA值和缺失值的过滤,为保证数据的真实性,本文并没有对缺失值进行回填。考虑到行业机理,当风速小于切入风速时,风机不会启动;当风速大于切出风速时,风机会进行停机保护。因此,本文去除了小于风机切入风速(3 m/s)和大于风机切出风速(25 m/s)的数据。

1.2 算法模型

长短期记忆网络(LSTM)算法作为一种时间序列的深度模型,其输入应为时间序列数集。在经过处理后的t时刻数据设定为θi=(x1,x2,…,xi,…,xi+t),此时刻LSTM算法公式为:

ft=σf(Wf·[ht-1,xt]+bf)

(1)

it=σi(Wi·[ht-1,xt]+bi)

(2)

ot=σ0(Wo·[ht-1,xt]+bo)

(3)

(4)

(5)

ht=ot·tanh(Ct)

(6)

在输入训练时间序列数据集后,该模型在多次迭代(1 000次)后获得固定的权值W值和偏置b值。考虑到公式(1)-(6),长短期记忆网络(LSTM)算法模型可以简化为LSTM(θ|W,b)。

自由分布的LSTM算法模型假设LSTM算法输出符合某一条件概率密度函数(CPD),同时使用负对数最大似然值(NLL)作为迭代过程中的损失函数。相比较传统的基于误差数值的损失函数,基于统计概率的负对数最大似然值(NLL),具有更好的泛化性。该特性能够使所提出的模型在小样本状态下拥有更好的预测精度。自由分布的LSTM算法可简化为:

(7)

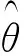
(8)

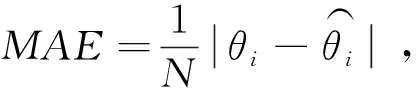
表1 模型参数

2 实际案例

在本文中,一个来自中国江苏2022年7月-8月的真实风场数据作为案例进行分析。其中训练集为1 000个观察数值,风速从3.01 m/s到15.73 m/s,其风速数据主要集中在(3 m/s～7.5 m/s)风速段,概率密度函数呈现‘偏态’状态,类似韦伯分布;测试集为4 500个观察数值,风速从3.01 m/s到11.42 m/s,其风速数据主要集中在(3 m/s～5 m/s)风速段并在(7 m/s～9 m/s)风速段也有一个副概率密度段,其概率密度函数呈现“两头”状态,类似2个正态分布组合分布。来自工业真实数据的训练集和测试集数据不符合同一个分布假设,如图1所示。本文使用Python 3.6,tensor-flow 2.0和tensor-flow probability 0.8 软件环境,单机i5-6200U CPU和8GB RAM硬件环境进行建模,模型运行时间为9.8 min。其硬件环境和软件环境不强依靠高端服务器算力,更具有工业应用推广性。

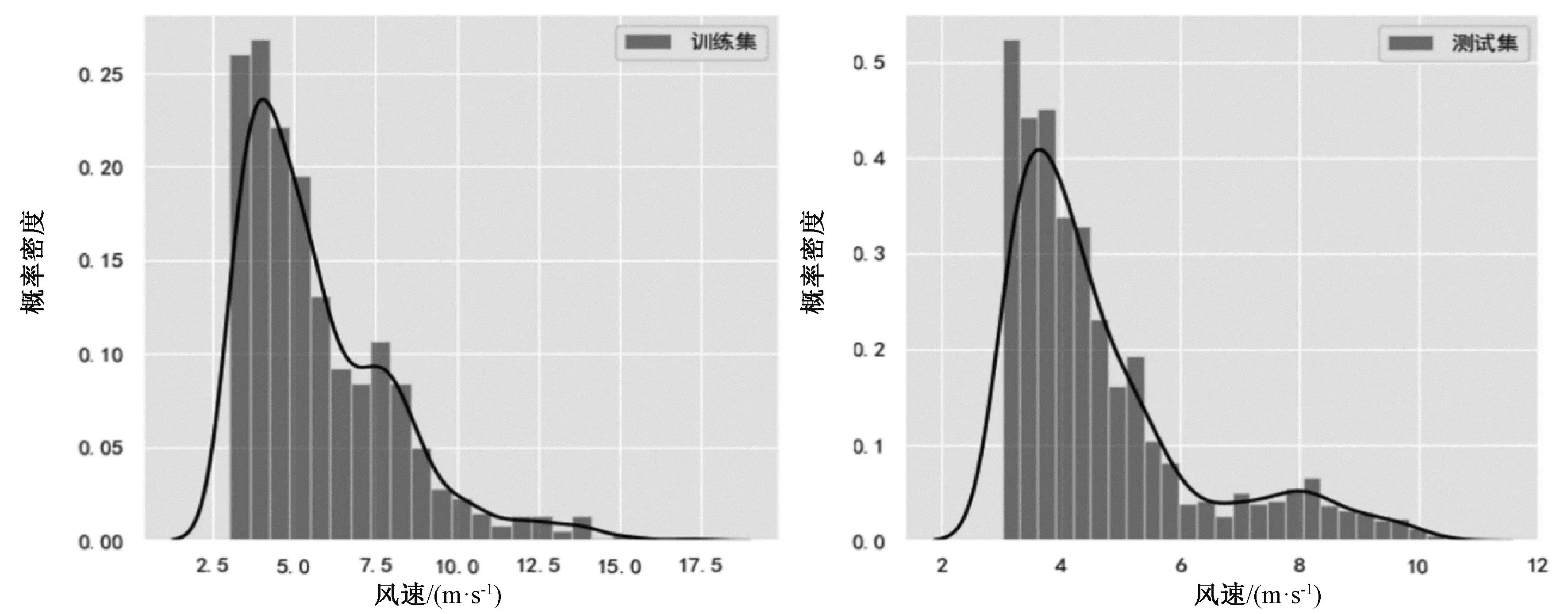
图1 风速数据分析

图2为在测试集1小时预测尺度下,自由分布LSTM算法和真实数据的比对,两者趋势相同。尤其是在观测值1 400时,在此前没有训练过的19 m/s风速下,自由分布LSTM算法依然能够很好地进行跟随,显示其具有优良的模型泛化性。图3为模型误差MAE自然对数值的监测图,本文使用自然对数能更好地监测出异常值,选用2倍最大训练集MAE自然对数值作为阈值(2),可以看出模型运行稳定,如后续出现持续超出阈值情况,即可通知算法人员,进行模型的重新训练。同时,表2为不同预测尺度(1小时、6小时、12小时、24小时、48小时)下,自由分布LSTM算法和传统LSTM算法的比对。自由分布LSTM算法的MAE值分别为:0.64(1小时),1.21(6小时),1.86(12小时)和2.28(24小时),而传统LSTM算法的MAE值分别为:0.77(1小时),1.33(6小时),2.01(12小时)和2.37(24小时)。在不同尺度下,从其统计指标均值-方差可以看出,自由分布LSTM算法(1.49～0.39)在多个预测尺度下均优异于LSTM算法(1.62～0.38),这证明该算法具有一定的工业应用性和推广性。

图2 测试集风速验证(1小时预测尺度)

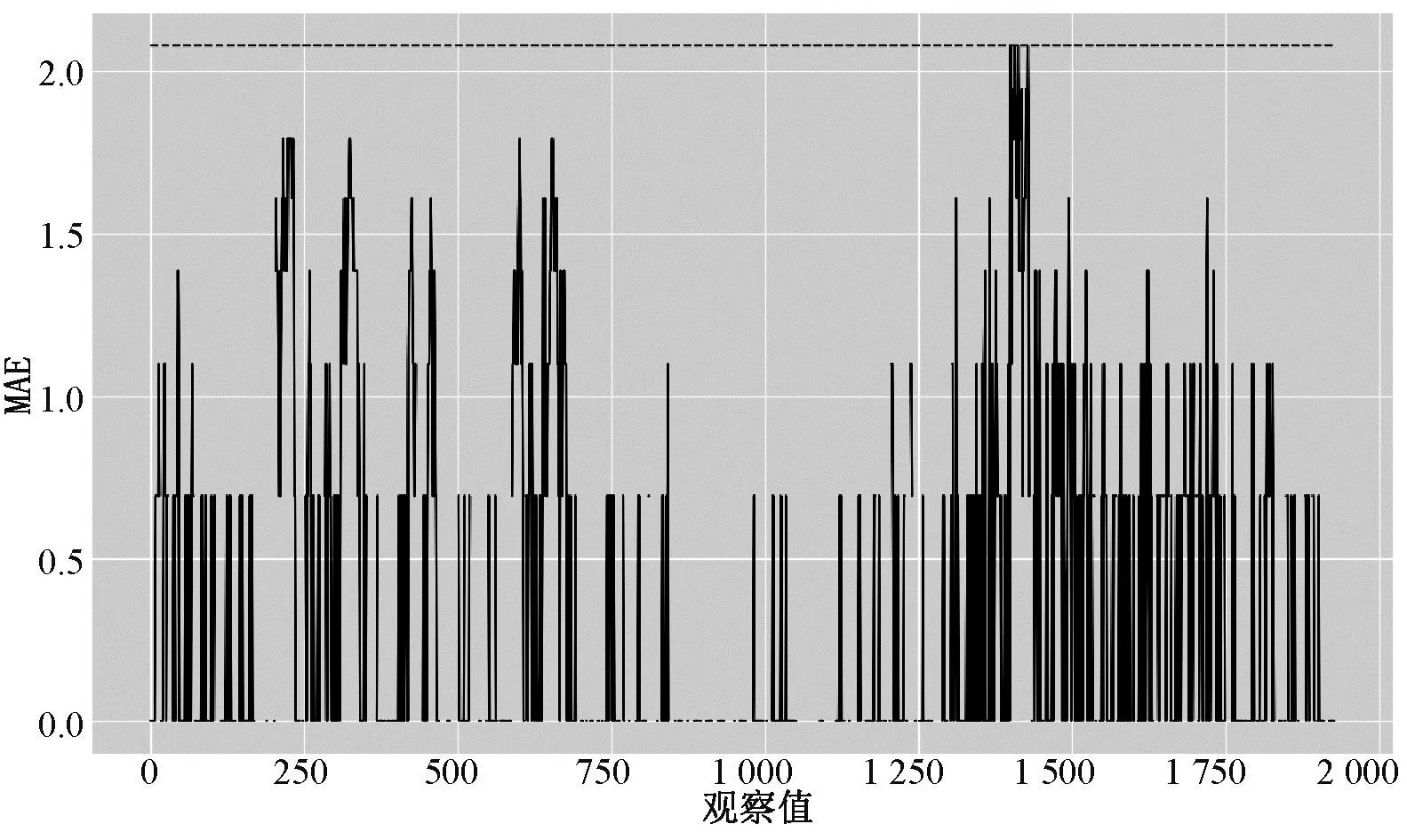
图3 模型状态监测(1小时预测尺度)

表2 MAE在不同尺度下的比较

3 结语

本文利用一种自由分布的LSTM算法对风速进行短时预测。自由分布的LSTM算法模型利用指数分布和泊松分布的共轭性,去除了特定概率密度函数假设对于风速预测精度的应用。通过和其他方法(LSTM算法)比对,该案可有效地对风速进行预测,在不同尺度下均表现出优异的效果,同时该方案还具有模型监测功能,用于模型迭代时间点的提醒。若风电场的运行维护人员根据预测结果,及时对风机状态进行校正处理,可提高风电场的发电量。未来,在基于该模型的基础上,可以继续探讨此模型在不同风场数据下的迁移性,以及模型在运行过程中的模型退化监测机制,为该模型在工业应用上的广泛性进行验证和推广。