基于3 种不同机器学习算法的滑坡易发性评价对比研究
王本栋,李四全,许万忠,杨勇,李永云
(1.攀枝花市自然资源和规划局,四川 攀枝花 617000;2.昆明理工大学国土资源工程学院,云南 昆明 650093;3.西南有色昆明勘测设计(院)股份有限公司,云南 昆明 650051)
滑坡作为世界上最常见的地质灾害之一,每年造成数千人伤亡和数千亿经济损失(Francisco et al.,2015;王朋伟等,2023)。对中国来说,由于多山地貌的特点,许多地区受滑坡影响严重(孙萍萍等,2022)。近年来,滑坡对环境、居民建筑和工业设施的威胁日益加重(Lin et al.,2012;孟晓捷等,2022;王海芝等,2022;黄煜等,2023),严重危害居民的生命财产安全,给国家和社会造成巨大损失(李宇嘉等,2022;田媛等,2022)。因此,丞需一种有效手段来减少滑坡带来的损害。开展科学、准确的滑坡易发性评价,对制定防灾措施具有重要指导意义。
一般来说,通过预测未来滑坡发生的位置和可能性大小,可以在一定程度上减少滑坡的破坏(Pradhan et al.,2010)。滑坡易发性因其对滑坡发生相对空间概率的预测能力,被认为是滑坡预防管理的重要工具,也是规避滑坡风险的首要选择(Dai et al.,2002)。近年来,滑坡易发性评价已成为热门研究课题。在区域尺度上,易发性评价模型可分为定性评估和定量评估两大类(贾俊等,2023)。随着计算机技术、遥感(RS)和地理信息系统(GIS)的飞速发展,滑坡空间数据的获取变得便捷,基于定量评估的易发性建模方法得到广泛应用(Shen et al.,2019)。例如,随机证据权重(Haydar et al.,2016;周宇等,2022)、逻辑回归(LR)(刘璐瑶等,2021;杜国梁等,2021)、BP 神经网络(唐睿旋等,2017;康孟羽等,2022;张林梵等,2022)、随机森林(RF)(刘坚等,2018;林荣福等,2020;马啸等,2022)和支持向量机(SVM)(Zhou et al.,2016;Zhu et al.,2022)等方法都在实际应用中取得较为理想的预测结果。在定量评估模型中,机器学习模型表现尤为突出,并被认为比基于专家意见的分析方法更有效预测山体滑坡(Binh et al.,2016)。SVM、BP 神经网络和RF作为3 种常见的典型机器学习算法,被广泛应用于滑坡易发性评价,并取得较高的预测精度。然而,受不同地质环境、数据背景影响,模型间的预测精度可能存在较大差异。目前的滑坡易发性研究大多是基于单一机器学习算法实施,缺乏不同算法之间的精度比较,难以获得研究区内更为准确的滑坡易发性结果。因此,有必要在特定区域内对多种学习模型进行比较,以选择高性能模型来获取区域滑坡预测结果。
鉴于此,笔者以云南芒市区域为例,分别基于SVM、BP 神经网络和RF 等3 种典型机器学习算法获取其区域滑坡易发性评价结果,并采用不同精度评价指标对其结果进行对比分析,以获得研究区最佳评价算法及结果。所得最优评价结果能为当地政府部门提供更加准确、可靠的防灾减灾参考依据。
1 研究区概况及数据源
1.1 研究区概况
研究区芒市地处云南省西南边境地区,隶属德宏傣族景颇族自治州,地理位置为E 98°05′~98°44′,N24°05′~24°39′(图1)。全境是以中、低山地为主的低纬山原地区,最高海拔2 890 m(风平镇),最低海拔528 m(中山乡)。山地面积占89%,山体多为东北至西南走向,东北高而峻峭,西南低而宽缓,向西南倾斜展布,河谷与断裂带走向一致,甚至发育在断裂带上。芒市属南亚热带季风气候,热量丰富,夏季湿润多雨,冬季温暖少雨,干湿季节分明。降雨主要集中在5~10 月份,年平均降雨量为1 653.4 mm,最多年为1 959.8 mm(杨平芬等,2014)。区内地貌涵盖侵蚀堆积地貌、岩溶地貌、构造剥蚀地貌、构造侵蚀地貌及火山堆积地貌5 大成因类型,其中以构造侵蚀地貌和岩溶地貌为主(郑迎凯等,2020)。

图1 研究区地理位置及样本分布Fig.1 Geographical location of the study area and distribution of sample
近年来,该区域大肆开展道路修建和矿产资源开采等人类工程活动,致使原有的生态环境遭到破坏。加之境内地质构造复杂,新构造运动强烈,为地质灾害的发育提供了有利条件,从而引发泥石流、崩塌和滑坡等一系列灾害的频繁发生,严重威胁了区内居民的生命财产安全。
1.2 数据来源
笔者采用的主要实验数据来源如下:①250 m 空间分辨率的岩性图,来源于地学服务平台。②30 m 分辨率的土地利用数据,来源于中国科学院资源环境科学与数据中心。③30 m 分辨率的DEM,来源于美国航空航天局NASA SRTM,用于地形地貌信息提取。④0.1°×0.1°空间分辨率的降雨数据,来源于美国航空航天局NASA GPM,通过反距离权重插值法获取区域内年均降雨量。
1.3 评价因子
实验采用100 m×100 m 分辨率的栅格作为评价单元,研究区共计289 609 个栅格单元。结合研究区历史资料、现场勘探及遥感影像目视解译,共获得565个滑坡点作为滑坡基础样本数据,并利用GIS 随机生成相等数量的非滑坡点(黄武彪等,2022)(图1),一同作为模型输入的因变量,记发生滑坡为1,未发生滑坡为0。在此基础上,按照7∶3 的比例将样本数据进行划分(Vijendra et al.,2019),70% 用于模型训练,30%用于模型精度测试。
在当前的滑坡易发性建模中,对于评价因子的选取并没有固定标准,唯一的原则是保证因子可操作、可测量和非冗余(Ayalew et al.,2005)。因此,在保证评价因子客观准确的前提下,结合研究区具体特性,选取9 个评价因子:高程、坡度、坡向、平面曲率、剖面曲率、起伏度、地层岩性、年均降雨量和土地利用,作为模型输入的自变量,并引入灰色关联分析对所选评价因子与研究区历史滑坡灾害之间的关联性进行检验,得出灰色关联排序(周定义等,2021)。按关联度从小到大依次为坡向(0.52)、地层岩性(0.59)、年均降雨量(0.66)、坡度(0.70)、高程(0.74)、起伏度(0.75)、剖面曲率(0.78)、平面曲率(0.81)、土地利用(0.82)。关联度最低的评价因子为坡向,其关联度为0.52,均大于0.5,从排序结果可以看出选取的9 个评价因子与研究区历史滑坡灾害之间存在一定的关联性,均能够作为该区域滑坡易发性建模的输入变量。
此外,为保证因子间统一的栅格单元大小,还利用重采样工具将栅格单元采样为30 m×30 m 分辨率,并据以往研究者经验(Adnan et al.,2013;Markus et al.,2015)与灾害点分布规律对各评价因子进行分级(图2)。

图2 评价因子分级Fig.2 Evaluation factor classification
2 研究方法
2.1 支持向量机(SVM)
SVM 是一种有监督的机器学习算法,基本原理是通过将低维度空间内混杂的、不可划分的数据投影到高维度空间内,并在相应的高维度空间内寻找最优分类超平面,以实现数据的正确分类(Huang et al.,2020)。
首先假设一组数据为(xi,yi),i=1,2,···,n,通过线性回归函数f(x)=ω·x+b拟合并确定ω 和b。采用松弛变量ε 来控制分类误差,相应得线性函数拟合为(黄发明等,2022):
当 ξi、大于0 时表示有分类错误,此时变换为求解最小化函数问题,如公式(2)所示,其中常数C大于0 为超出分类误差ε 的错分程度,将其带入拉格朗日函数后的线性拟合函数如公式(3)所示。
式中:ω 为确定超平面方向的权重向量;b为偏差;C为惩罚因子;αi、为支持向量机系数。
2.2 BP 神经网络(BPNN)
BP 神经网络由Hinton(1986)于1986 年提出,是一种按误差反向传播算法训练的多层前馈网络,分别由信息的正向传播和误差的反向传播两个过程组成(陈玉萍等,2012)。该算法的模型结构和权值通过学习过程获得,学习过程分为多层前馈和反向误差修正两个阶段(李东等,2015)。多层前馈数学模型为:
误差的反向传播阶段采用梯度递降算法,通过调节各层神经元之间的连接权值,使总误差向减少方向变化。其表达式为:
则权值调整公式为:
2.3 随机森林(RF)
随机森林是一种组合分类模型,它由多棵决策树{h(X,Θk),k=1,2,···n} 组成。参数集{Θk}是独立同分布的随机向量,在给定自变量X的情况下,最优分类结果由每棵决策树模型投票选出(吴孝情等,2017)。其表达式为(Pham et al.,2018):
式中:m_vote为投票结果。
2.4 模型精度检验
为有效地评估3 种算法对滑坡易发性的预测能力,笔者采用受试者工作特征曲线(Receiver-Operating Characteristic,ROC),曲线下面积(Area Under Curve,AUC)以及准确度(Accuracy,ACC)对模型的性能进行评价。ROC 曲线以真阳性率(TPR)为纵轴,以假阳性率(FPR)为横轴,曲线越靠近左上方,AUC 值越大,判别滑坡发生的精度越高。ACC 则依靠混淆矩阵计算,它能够度量样本被正确分类的比例,ACC 值越接近1,说明模型准确性越高。
3 结果与分析
3.1 多重共线性分析
初步选取的滑坡评价因子之间可能存在统计学上的共线性关系,从而使得模型估计失真或难以准确描述因子与滑坡之间的真实关系(王毅等,2021)。因此,在滑坡易发性建模之前,还需检验因子间是否存在共线性问题。
通常采用VIF(方差膨胀系数)和容差两个指标来分析评价因子间的共线性情况,当容差值小于0.1 或VIF 值大于10 时,表示因子间具有较高的共线性程度,需对其进行剔除(Ryuta et al.,2019)。利用SPSS20 获取评价因子间的共线性关系(表1),所有因子的容差值均大于0.1,VIF 值均小于10,表明因子之间不存在强共线性关系,均可用于后续的滑坡易发性建模。

表1 评价因子多重共线性分析结果Tab.1 Results of multiple covariance analysis of evaluation factors
3.2 滑坡易发性评价结果对比分析
实验利用GIS 多值提取功能,将各评价因子的分级属性值提取为前文的样本数据,然后基于Matlab 语言下的libsvm 框架构建SVM 模型,SPSSPRO 构建BP 神经网络模型和RF 模型,以此对研究区289 609个栅格单元进行滑坡易发性指数计算,输出0~1 之间的滑坡概率值,并导入到Arcgis10.7 中。采用自然间断法(Chen et al.,2017)将其划分为5 个等级:极低易发、低易发、中易发、高易发和极高易发,以此得到3 种算法下的芒市区滑坡易发性评价结果(图3)。
3 种算法评价得出的研究区滑坡易发性结果(图3)在空间位置分布上存在一定的相似性和差异性。具体而言,在3 种算法得到的易发性结果中,极高易发区集中分布在五岔路乡和江东乡一带,说明这一带相对其他区域,发生滑坡的可能性较大,和前人研究结果(郑迎凯等,2020)相一致;极低易发区则主要分布在轩岗乡、芒市镇以及风平镇,这些区域由于地势平坦,地形地貌简单,不利于滑坡发生,因此被赋予了较低的易发性等级。从上述几个典型区域的易发性等级划分来看,3 种算法得到的结果都与实际情况具有较高的吻合度。三者之间的差异性则体现在遮放镇、勐戛镇一带的南部地区,这些地区在BP 神经网络和RF 得到的评价结果中几乎被赋予了中易发等级;而在SVM 结果中,却被赋予了极高易发等级,不同算法对研究区内评价因子与滑坡易发性的非线性拟合能力可能是造成差异的首要原因,即算法的性能不同,所获取的易发性评价结果的准确性也有所不同。
通过定性方面的比较,并不能得出3 种算法的优劣。因此,下文将从定量的角度对模型评价结果的准确性进行详细分析,以获得芒市地区最佳易发性评价模型。
3.3 评价精度对比分析
为对模型评价结果的准确性进行量化分析,采用统计的方式计算出模型测试样本的ACC 值(表2),并在SPSS 20 中绘制3 种模型的ROC 曲线(图4)。结合表2 和图4 可以看出RF 模型的ACC 值和AUC 值最高分别为0.867 和0.94,BP 神经网络次之为0.829 和0.90,SVM 最低为0.794 和0.88。RF 算法无论是ACC值还是AUC 值,均优于其他两种算法,AUC 值较SVM 和BP 神经网络分别提升了4%和6%,表明在芒市地区,RF 模型具有更高的滑坡预测能力。

图4 测试样本ROC 曲线Fig.4 Test sample ROC curve
此外,科学合理的滑坡易发性评价结果还需满足两个标准:①随着易发性等级增加,分级面积占比逐渐减小。②随着易发性等级增加,滑坡比(Sei)逐渐增大(Harlow et al.,2005)。在本研究中,滑坡比为实际滑坡点落入各级易发区的百分比(Dei)与各级易发区面积占总面积的百分比(Mei)的比值(Sei)(i=I,II,III,IV,V)。
由表3 可知3 种算法均满足上述两个准则,从极低到极高,易发性分区面积比(Mei)逐级递减,Sei值逐级递增。尽管如此,由于数值差异,它们的合理性依然具有一定的可比性。极低易发区的SeI值越小,极高易发区的SeV值越大,模型的合理性越高(刘希林等,2017)。检验结果显示在SVM、BP 神经网络、RF 评价结果中,分别有74.69%、82.30% 和86.91% 的滑坡点落入高易发等级以上区域,SeI和SeV值分别为0.19和6.85,0.11 和9.14,以及0.07 和9.21,最小SeI值和最大SeV值均为RF 算法所得,说明RF 芒市区滑坡评价结果的合理性要优于其他两种算法。
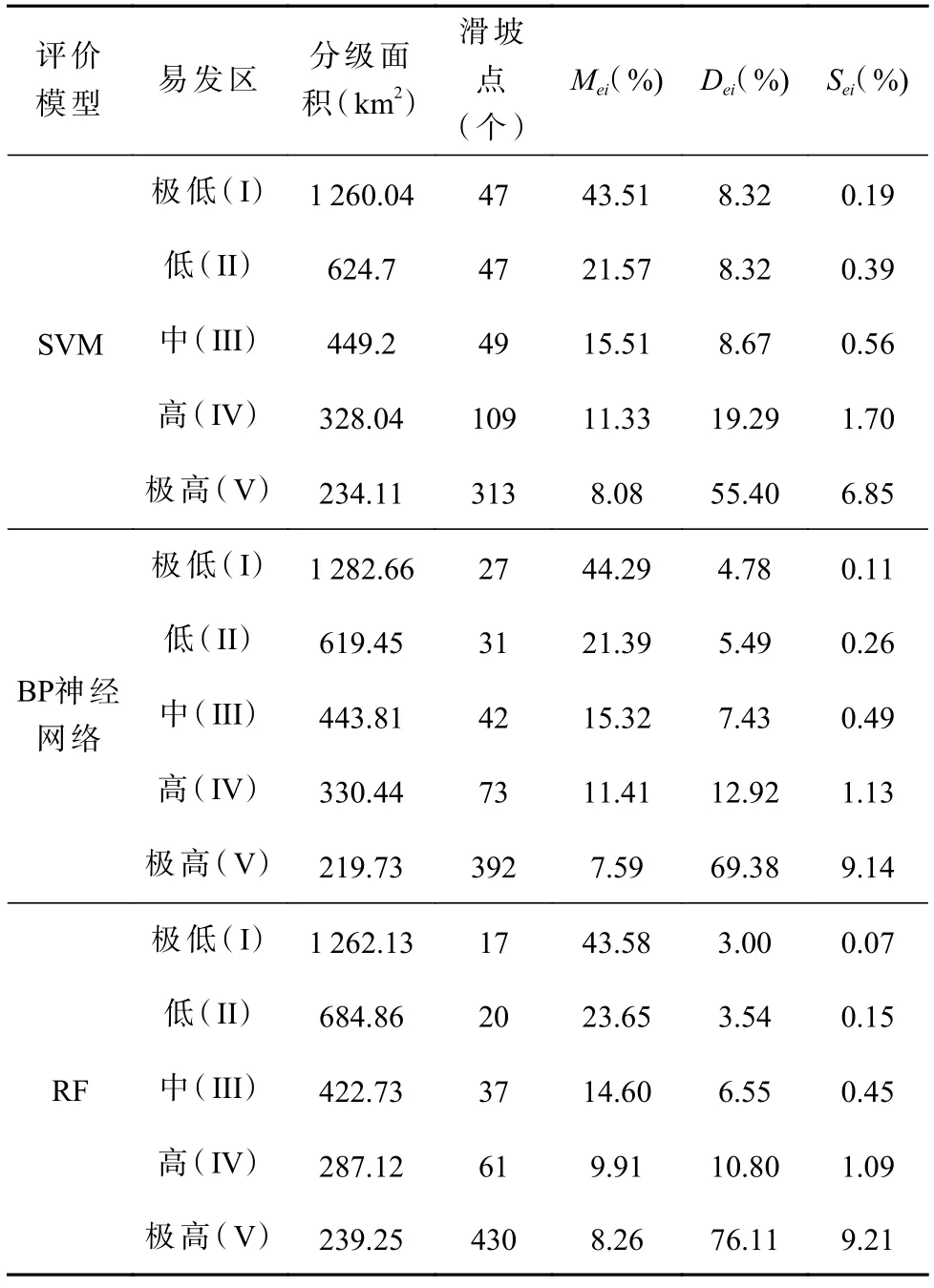
表3 易发性分区合理性检验结果Tab.3 Rationality test results of susceptibility zoning
3.4 野外考察验证分析
根据野外实地考察,发现遮放镇新增一处滑坡,该滑坡位于垦西社区七队,长约30 m,宽约60 m,属于小型滑坡,虽没有人员伤亡,但仍旧对周边设施造成了破坏。本次实验利用该滑坡对3 种算法的灾害预测能力进行评估,进一步对比验证模型的准确性。
此次滑坡的发生对附近的植被、道路、居民建筑造成一定程度的损坏。如图5d~图5e 所示,受该滑坡影响,在一户居民家中发现约1~2 m 长的拉张裂缝;坡体边缘植被倒塌,道路中央也出现长约12 m 的裂缝,由于滑坡规模较小,并未带来较为严重的损失。由图5a~图5c 可知,这次滑坡的空间位置分别位于SVM 滑坡易发性评价结果的极低易发区,BP 神经网络的中易发区,RF 的高易发区。从3 种评价结果的等级划分来看,RF 算法对此次滑坡进行了很好的空间位置预测,得到与实际情况更为一致的滑坡预测结果。
综上可知,无论是评价结果分级的合理性,还是滑坡预测的准确性,RF 算法在芒市的滑坡易发性评价应用中都表现出明显的优势,相比其他两种算法更适合用于该区域的易发性评价结果获取。这也说明即使在同一区域,相同的地理环境条件,不同模型获得的结果也会不尽相同。通过不同模型对比的方式,可以获得更为准确、可靠的研究区易发性评价结果。
4 结论
(1)3 种算法获得的滑坡易发性结果在极低和极高易发区的空间位置分布上具有较高的一致性,极低易发区集中分布在轩岗乡、芒市镇以及风平镇区域,极高易发区分布在五岔路乡和江东乡一带。
(2)利用SPSS 绘制3 种算法的ROC 曲线,得到SVM、BP 神经网络和RF 的AUC 值分别为0.88、0.90、0.94。RF 的AUC 值较SVM 和BP 神经网络分别提升5.2%和3.2%,表明RF 算法在芒市地区的滑坡预测能力要优于其余两种算法。
(3)通过对滑坡比值(Sei)进行统计,发现SVM、BP 神经网络和RF 在极低易发区的SeI值分别为0.19、0.11 和0.07,在极高易发区的SeV值分别为6.85、9.14和9.21。SeI的最小值和SeV的最大值均由RF 算法所得,并且该算法还得到与实地考察情况更为一致的滑坡评价结果。充分说明RF 算法获得芒市滑坡易发性结果的准确性高于其他两种算法,能够为该区域的防灾减灾提供可靠参考。

