基于活动性检测动态估计噪声的心音降噪算法

许春冬，辛鹏丽，闵 源+，应冬文，2，周 静，李海兵

(1.江西理工大学 信息工程学院，江西 赣州 341000；2.中国科学院大学 电子电气与通信工程学院，北京 100049)

0 引 言

心音信号蕴含着大量心脏和周边血管功能状态的生理与病理信息[1，2]，是心血管疾病临床诊断的重要依据之一[3]。然而，在进行心音信号的采集与处理时，由于心音信号能量较弱[4]，致使其极易受到来自外部环境噪声、采集设备自噪声及人体其它生理器官杂音等噪声的干扰[1，2，5]。这些噪声的存在往往会导致心音信号的质量降低，进而对后续的分析与诊断结果造成严重的干扰[1，6]。

近十几年来，国内外学者提出了许多心音降噪的方法，主要可分为3类：基于小波的心音降噪方法、基于经验模态分解的心音降噪方法、基于噪声功率估计的心音降噪方法[7-10]。虽然上述算法均取得了一定的降噪效果，但仍存在一定的不足，例如基于小波的心音降噪算法[7，8]在处理异常心音时易造成心音丢失；基于经验模态分解的降噪方法[9，10]容易使降噪后的心音信号出现失真或低、中频噪声残留。基于噪声动态估计的方法[11]存在低频噪声残留和部分心音失真的问题。

针对上述心音降噪算法所存在的不足，本文提出了一种基于心音活动性检测动态估计噪声的心音降噪算法(后文中均称为HSAD-IMCRA算法)。该方法通过设计的HSAD方法来判断心音帧是否为基础心音，并对基础心音和非基础心音中的噪声采用不同的方法进行估计，从而克服了传统噪声估计的不足，能够在保证心音信号不失真的情况下，实现最大程度的噪声抑制。

1 算法框架

提出算法的流程如图1所示。首先，该算法将时域含噪心音信号经短时傅里叶变换(short-time Fourier transform，STFT)变换到频域，并根据心音信号的结构特点[12]，设计适合的HSAD方法，判别基础心音(fundamental heart sound，FHS)与非基础心音(non-FHS)成分；其次，分别采用IMCRA和递归平滑的方法进行噪声估计；然后，通过估计的噪声功率谱与含噪心音的前后帧信息来估计非因果先验信噪比(signal-to-noise ratio，SNR)，求取干净心音估计器的增益函数GLSA[13]；最后，结合原始相位信息，通过逆STFT(ISTFT)重构时域降噪心音。其中，采用非因果SNR估计方式代替因果SNR的估计方式，更准确地估计了FHS出现和截止边缘部分及一些异常突变心音信号的先验SNR[14，15]，在一定程度上减少了FHS的失真；采用HSAD辅助噪声估计，能更准确地跟踪噪声功率的变化情况，从而减少了噪声的残留。

图1 心音降噪算法流程

2 算法原理

2.1 MMSE-LSA算法原理

由Ephraim等[16]提出的最小均方误差对数幅度谱(minimum mean square error of log-spectral amplitude，MMSE-LSA)估计算法通过对声学信号进行最优幅度谱估计[17]来恢复干净信号，相较于一些经典的降噪算法，能更有效降低信号失真[18]，提高信号的可分析性，故适用于心音信号的降噪处理。假设心音与噪声不相关[13]，设s(n) 为干净心音，d(n) 为噪声，则含噪心音y(n) 可表示为

y(n)=s(n)+d(n)

(1)

对y(n) 进行短时傅里叶变换[12，13]，可得

Y(k，l)=S(k，l)+D(k，l)

(2)

将式(2)表示为极坐标形式[13]

R(k，l)ejφ(k，l)=A(k，l)ejφ(k，l)+N(k，l)ejϑ(k，l)

(3)

其中，l和k分别代表帧数和频点数的索引，Y(k，l)、S(k，l)和D(k，l) 分别是y(n)、s(n) 和d(n) 进行STFT后的结果，R(k，l) 和φ(k，l) 分别是Y(k，l) 的频谱幅度和相位；A(k，l) 和φ(k，l) 分别是S(k，l) 的频谱幅度和相位；N(k，l) 和ϑ(k，l) 分别是D(k，l) 的频谱幅度和相位。

(4)

(5)

(6)

其中，ζ1(k，l)=λS(k，l)/λD(k，l) 为先验信噪比，γ1(k，l)=|Y(k，l)|2/λD(k，l) 为后验信噪比，λS(k，l) 为心音功率谱，λD(k，l) 为噪声功率谱。

2.2 非因果先验信噪比估计

在增益函数GLSA(k，l) 的求解过程中，用非因果信噪比[15]代替因果信噪比，能更准确估计存在突变心音信号或脉冲干扰噪声时[13]的噪声功率。在非因果信噪比的估计中，利用第0至l+M帧含噪心音来估计第l帧的先验信噪比[15]，而不是局限于使用前一帧信息。

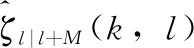
(7)

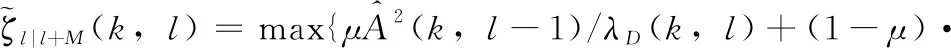
(8)

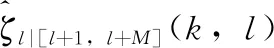
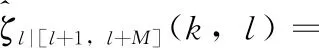
(9)

2.3 噪声估计

2.3.1 IMCRA噪声估计算法

(10)

基于最小均方误差(minimum mean square error，MMSE)的准则下[13]，噪声功率谱的估计如式(11)所示[13，20]

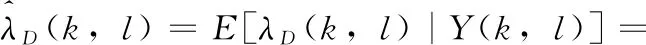
(11)

(12)

α2=α+(1-α)·P(k，l)

(13)

式(13)中，心音存在条件概率P(k，l)， 可通过贝叶斯公式[22]计算得到，如式(14)和式(15)所示

(14)

(15)

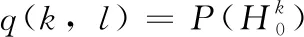
第一次迭代过程中，根据判决准则对是否存在基础心音进行粗略估计[19]，如式(16)所示

(16)

其中，γ0和ζ0为常数阈值参数，基础心音存在时I(k，l) 为1，基础心音不存在时I(k，l) 为0。γmin(k，l) 和ζ2(k，l) 的定义如式(17)和式(18)所示

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

其中，γ3为常数阈值。

2.3.2 基于HSAD-IMCRA的噪声功率估计

传统的基于MMSE-LSA的降噪算法采用IMCRA方法对信号噪声功率谱进行估计，但IMCRA噪声估计对基础心音开始边缘部位的先/后验信噪比参数估计往往偏低，易造成降噪后的心音信号出现基础心音成分失真。此外，若心动周期内存在人体其它器官引起的额外噪声，也易造成先/后验信噪比偏高，使得噪声残留。而心音信号主要是由第一心音(S1)、收缩期(Sys)、第二心音(S2)、舒张期(Dia)这4个状态组成[9]，且具备一定的周期性[7，9]，可对应图2所示。其中，Sys和Dia一般不包含基础心音信号成分，表现为噪声特性，故可根据递归平滑法来估计并更新噪声功率谱[20]，获得更为准确的先/后验信噪比估计结果。而S1和S2持续时间段是由噪声和基础心音信号混叠构成，故采用IMCRA对噪声进行有效追踪，动态估计噪声功率谱并更新[22]。需要额外指出的是，IMCRA噪声估计过程中，采用2.2节所述非因果信噪比计算方式替换因果信噪比的计算方式，减小心音失真情况的出现。

图2 心音信号时域波形

故本文算法中采用HSAD-IMCRA的算法来估计当前含噪心音帧的噪声功率谱，能进一步降低估计的干净心音的失真和噪声残留。所提算法噪声功率谱估计流程如图3所示。

图3 HSAD-IMCRA算法噪声功率谱估计流程

活动性检测是声学信号处理领域里较为常用的处理手段，且类别繁多[13，20]。为了在有效检测心音活动性的前提下进一步考虑低的算法复杂度，本文采用对数频谱距离(logarithmic amplitude spectrum distance，LASD)来设计适合心音信号的HSAD方法，用于判别基础心音帧和非基础心音帧[21]。基于前几帧为非基础心音帧的假设，可通过式(28)将LASD计算如下

(28)

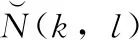
(29)

T(l)=τD(l-1)+(τ-1)D(l)，τ>1&T(l)>D(1)

(30)

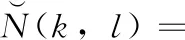
(31)

其中，ρ(l-1)=1表示前一帧为基础心音帧，ρ(l-1)=0表示前一帧为非基础心音帧，NIMCRA(k，l) 为IMCRA算法估计的噪声幅度谱，τ为自适应阈值平滑参数，αn为平滑因子[20]。

此外，根据式(31)的原理，噪声功率谱的平滑估计λD(k，l) 可表示如下

(32)

其中，λIMCRA(k，l) 为IMCRA估计的噪声功率谱，在获得估计的噪声功率谱后，即可计算先/后验信噪比，并按式(5)获得增益函数GLSA，从而重构出干净心音信号。实验中所涉及的参数设置见表1。

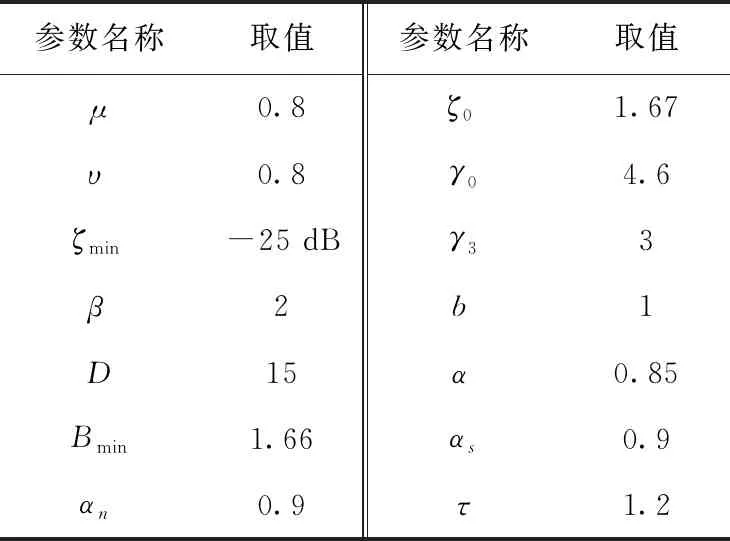
表1 参数的取值

3 实验仿真与结果分析

3.1 实验数据

实验仿真所用数据集由公开数据集(https：//github.com/yaseen21khan/Classification-of-Heart-Sound-Si-gnal-Using-Multiple-Features-)[23]和自采集心音数据集[24]两部分组成，共计1030条。参考文献[10]指出，高斯白噪声是心音信号中的主要噪声成分，故本文主要以去除高斯白噪声为主。在实验仿真中，从构建的数据集中抽取出80条相对干净的正常心音、320条相对干净的异常心音，并将高斯白噪声分别以0 dB、5 dB、10 dB、15 dB、20 dB的SNR叠加到抽取的心音信号中[10]，构建含噪心音数据集，且所有心音信号均降采样至2000 Hz。

3.2 HSAD-IMCRA噪声估计性能分析

为了验证HSAD-IMCRA算法的噪声估计性能，将其与IMCRA噪声估计性能进行了对比。选用的评测指标为对数似然比(log likelihood ratio，LLR)和加权谱斜率(weighted spectral slope，WSS)[13，20]。其中，LLR是对频谱距离的度量，取值范围在0～2之间，估计的干净心音与原始干净心音间的LLR越小，即噪声估计越准确[13]；WSS是对频带谱斜率之间加权差距的度量，WSS越小，则估计的干净心音与原始干净心音越接近，即噪声估计越准确[20]。噪声估计算法相关指标对比结果如图4所示。

图4 噪声估计算法相关指标结果对比

图4(a)和图4(b)分别是基于IMCRA算法和基于HSAD-IMCRA算法估计的干净心音与真实的干净心音间的LLR与WSS的对比结果。显然，基于HSAD-IMCRA算法的WSS和LLR评测结果均低于IMCRA算法，这表明基于HSAD-IMCRA算法的噪声估计性能要优于IMCRA算法。

3.3 各类算法降噪结果的时频图对比

提出算法与基于小波阈值的降噪算法[8]、基于OMLSA-小波的降噪算法[11]进行实验对比。其中，基于小波阈值降噪算法中采用的小波基为coif-5，分解层数为5层，阈值函数为自适应非线性阈值；基于OMLSA-小波降噪算法中，先通过OMLSA对含噪心音降噪，再利用小波降噪算法对OMLSA降噪后的心音继续降噪处理，其中小波降噪算法中的相关参数参考文献[11]。算法降噪性能的评测指标为输出SNR和均方根误差(root mean square error，RMSE)[2]。

采用3种降噪算法对公开数据集和自采集的心音信号进行降噪，来验证各类算法的降噪效果。其中，公开数据集中的数据相对比较干净，故对该类数据集中的心音进行降噪之前，将高斯白噪声以10 dB的SNR分别叠加到所选的心音中，来构建含噪心音。而部分自采集数据集中本身含有大量的噪声，故不对其进行加噪处理。各类算法对不同类型心音的降噪结果如图5所示。

图5 3种算法对不同类型心音的降噪结果

图5(a)、图5(b)和图5(c)分别是上述3种算法对正常/异常心音降噪后的时域波形图和频谱图的对比结果。其中，图5(a)和图5(b)分别使用的是公开数据集中的正常心音和异常心音，而图5(c)使用的是自采集心音数据集的正常心音。为了便于对比分析，图中用椭圆进行标记。从图5(a)和图5(c)的时域波形图中可以看出，基于OMLSA-小波算法因将部分边缘有用信号和及其微弱的杂音当成噪声信号进行估计造成后期估计的基础心音成分有所丢失，而基于小波阈值算法和本文算法降噪后的波形与原始心音波形差别不大；然而，从图5(a)和图5(c)的频谱图中可以看出，基于小波阈值算法能通过频带去除高频和低频噪声使非基础心音部分残留的噪声较少，但基础心音部分却因为丢失的高频和低频分量中包含部分有用心音成分而造成了FHS的失真。另外从图5(b)的时域波形图和频谱图中也可以看出，基于小波阈值算法和基于OMLSA-小波算法在对噪声去除的同时将噪声和基础心音信号混叠构成的异常心音信号成分一同丢失，导致出现较为明显的心音失真，且基于OMLSA-小波算法降噪后的心音在非基础心音部分仍存在部分中频噪声。相比上述两种算法，本文算法可使心音信号在减小FHS失真的前提下，更为有效地抑制噪声，重构出一个更为平滑自然的频谱，更加符合后续分类处理的需求。综上时频图的对比分析来看，提出算法较基于小波阈值的算法和基于OMLSA-小波的算法更优。

3.4 各类算法降噪结果的指标评测

此外，本文对3种算法的降噪性能进行了客观的对比，评测所用心音包括正常心音(N)与异常心音。其中，异常心音为二尖瓣反流(mitral regurgitation，MR)心音、二尖瓣脱垂(mitral valve prolapse，MVP)心音、二尖瓣狭窄(mitral stenosis，MS)心音和主动脉狭窄(aortic stenosis，AS)心音4类[23]。3种算法对不同信噪比的正常与异常心音降噪后输出SNR的统计平均值见表2。输出SNR值越大，表示算法的降噪性能越好[2，6，7]。

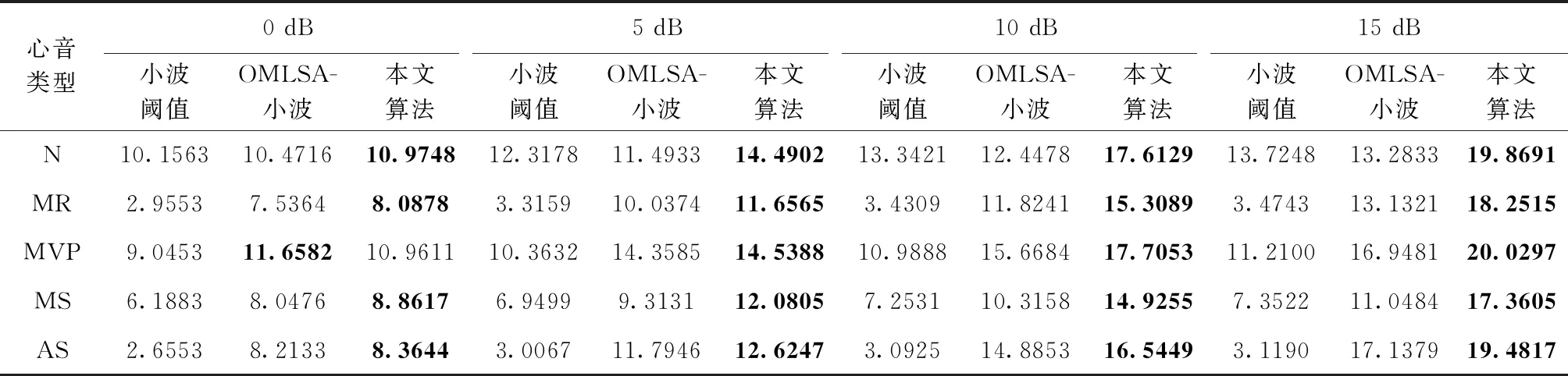
表2 对不同信噪比的含噪心音降噪后的SNR

从表2中可以看出，基于OMLSA-小波算法和基于小波阈值算法要明显低于提出算法的输出SNR；原因是前两种算法降噪后的心音信号残留了较多的中频噪声，且存在FHS失真，尤其是异常心音更为明显。而提出算法对SNR为0 dB的MVP所得SNR值要低于基于OMLSA-小波算法，这是源于提出算法中的IMCRA为了防止噪声过估计，使部分噪声残留，而MVP相对其它类型的心音残留的噪声较多，但整体上对多种类型的心音有着较好的降噪效果，且能在保证心音信号不失真的前提下，对噪声最大程度的抑制。

鉴于SNR的部分不良表现，故进一步通过RMSE来检验3种算法在降噪中对正常心音与异常心音的失真与降噪平衡度。RMSE越小，表示降噪后的心音越接近于真实干净心音，即降噪性能越好[2，6，7]，反之降噪性能越差。从数据中抽选N、MVP、MS和MR这4种类型的心音，利用3种算法分别对不同信噪比下的4类心音进行降噪处理，其RMSE对比结果[2]如图6所示。

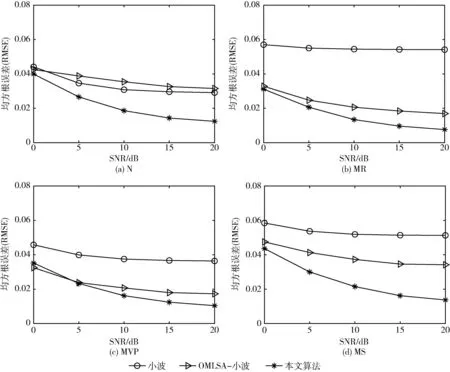
图6 不同信噪比的4类心音降噪后的RMSE对比曲线

从图6中可以看出，随着噪声水平的降低，提出算法的RMSE也逐渐减小。图6(a)显示，SNR为20 dB时，提出算法降噪后的RMSE为0.0124，说明降噪后的信号与原始信号之间相似度较高，即降噪效果较好；SNR为0 dB时，提出算法降噪后的RMSE为0.0399，降噪后的信号与原始信号之间相似度降低，降噪性能下降；这是因为低SNR下，为了确保FHS无失真引起了部分噪声残留。从图6(a)、图6(b)、图6(c)和图6(d)可以看出，除图6(c)中因防止噪声过估计造成MVP信号内残留部分噪声，从而使提出算法在0 dB～5 dB间的RMSE值略高于基于OMLSA-小波的算法之外，其余情况下，提出算法对N、MR、MVP和MS这4种类型心音进行降噪所得RMSE值均低于对比算法，说明提出算法降噪后的信号更接近于原始干净心音信号，能较好地保留FHS成分，更为适用与不同噪声水平下的多种类型心音降噪。

4 结束语

本文根据心音信号的基本特征，设计HSAD方法判决当前心音帧是否为基础心音帧，并分别采用递归平滑和IMCRA动态对非基础心音和基础心音的噪声功率进行估计与更新。该方法一方面结合HSAD，来减小收缩期和舒张期杂音对噪声估计的影响，弥补IMCRA的不足，减小杂音和噪声的残留；另一方面采用非因果信噪比替代因果信噪比，避免了由非基础心音向基础心音过渡时先/后验信噪比偏小的问题，减小了基础心音成分的失真。