基于价值滤波的空战机动决策优化方法

付宇鹏，邓向阳，2，*，朱子强，张立民

1.海军航空大学 航空作战勤务学院，烟台 264001

2.清华大学 自动化系，北京 100084

随着电子对抗技术的发展和战机隐身性能的提高，未来仍存在视距内空战的场景［1］，对抗双方如何根据当前作战态势选择精确有效的机动决策仍然是重要的研究方向［2］。为了提高训练效能，飞行员对抗训练中需要具有决策能力的智能化、风格化的陪练对手［3］。

2020 年，DARPA 举办Alpha Dogfight 狗斗大赛，最终美国苍鹭公司获得冠军，洛克希德·马丁公司获得亚军［4］。并且苍鹭公司的AI 在人机对抗中以5：0 完胜人类飞行员。同年11 月，中国航空工业成都飞机设计研究所举办人工智能空战大赛，是相关单位第1 次组织如此大规模人工智能对战。2021 年开始，中国指挥与控制学会每年主办全国空中智能博弈大赛，吸引全国各机构队伍参赛。与传统方法不同的是，各赛事中各参赛队伍越来越多采用强化学习（Reinforcement Learning，RL）和模仿学习（Imitation Learning，IL）算法实现机动决策控制。

强化学习是一个旨在学习某种控制策略的过程，该策略可以最大化智能体获得的奖励［5］。结合深度神经网络优秀的函数逼近能力，深度强化学习已被证明即使在复杂的连续动作空间也可以解决许多困难的任务并获得超过人类专家的性能，具备近距格斗这类复杂场景的飞行机动决策控制的能力。

强化学习在飞行控制系统、航路规划、空战博弈等领域取得了一定的进展，文献［5-6］设计了基于强化学习算法的姿态控制器，验证了神经网络模型控制固定翼飞机的可行性。文献［7］利用经验池Actor-Critic 算法，通过选择原子动作实现了固定翼飞机轨迹跟踪，为机动决策系统架构设计提供了宝贵的思路。文献［2］采用基于原子行为的分层马尔科夫决策过程，利用双深度Q网络（Double Deep Q-Network，DDQN）算法训练网络模型，实现了机动决策控制。基于原子行为的控制模型仿真精度和真实性受限于离散动作空间粒度，随着离散动作空间的增长，模型训练难度和内存需求将大幅上升。而采用端到端模型，即智能体直接控制飞机发动机油门开度、升降舵、副翼、方向舵偏转，算法收敛难度大。文献［4］采用分层策略的架构，利用柔性动作-评价（Soft Actor-Critic，SAC）算法训练网络模型，取得了较好的效果，但模型结构复杂，训练周期长。文献［8］基于双延时确定策略梯度（Twin Delayed Deep Deterministic Policy Gradient，TD3）

算法，提出了基于价值的经验池样本优先度排序方法，提高了算法收敛速度。文献［9-10］提出了应用于超视距空战的机动决策方法，采用分层近端策略优化（Hierarchical Proximal Policy Optimization，H-PPO）算法，将动作空间映射到原子行为序列，分别实现了单机和多机的空战机动决策智能体建模。

面对空战对抗这类状态空间复杂的环境，基于强化学习的空战机动决策优化算法专家经验利用不足，往往难以保证算法快速收敛。针对该问题，提出了价值滤波（Value-Filter）概念，并提出了基于价值滤波方法的示例策略约束算法（Demonstration Policy Constrain，DPC）。主要创新在于，算法利用价值滤波方法提取回放经验池和示例经验池的优势数据，约束空战智能体策略优化方向，从而提高传统强化学习在线策略（on-policy）算法的收敛效率，并避免示例数据次优的问题。

1 研究背景

1.1 基于示例的策略优化问题

在复杂的智能体机动决策优化任务中，训练难点在于状态空间庞大，且大多数据无效，导致智能体消耗大量时间学会平稳飞行，因此需要示例数据给予启发式信息。少量的示例轨迹可以由人类专家或简单的策略模型收集，示例轨迹数据集定义为DE={τ1，τ2，…，τn}，其中τn=表示第n条飞行轨迹，由“状态-动作-奖励-状态”四元组序列构成。这些轨迹的质量可以用奖励函数来判断。基于示例数据的策略优化方法中，常用方法包括3 类：

1）利用模仿学习的策略优化方法。最常见的一类方式称为行为克隆（Behavioral Cloning，BC），直接通过监督学习的方式，从示例数据集的状态-动作对中学习策略。行为克隆技术在自动驾驶［11-12］，无人机导航控制［13-14］取得了进展。为了解决行为克隆技术存在的策略偏移和复合误差，提出了基于数据增广的DAgger 算法［15］，但该类算法需要长时间在线干预，在空战决策建模场景中不易实现。逆强化学习（IRL）是另一类模仿学习算法，通过示例推测奖励函数［16］，在无人机自主飞行控制，机械手臂等应用中取得一定成果［17-18］。但空战对抗问题状态空间复杂，示例策略分布往往不唯一或目标不明确，算法难以收敛。

2）将示例数据保存为示例经验池，利用离线强化学习算法进行训练。文献［19-20］将深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法与BC 算法相结合，利用BC 约束策略优化方向，在稀疏奖励下利用后验经验回放技术仍可获得较高回报。但离线强化学习存在策略偏移问题，往往需要在线细调。

3）行为克隆预训练，在线细调。AlphaStar［21］使用人类玩家对局数据和智能体自博弈数据结合训练生成策略，在星际争霸游戏中击败职业玩家。文献［22］将模仿学习应用于无人驾驶环境，实现智能体自主驾驶。文献［23］利用采集的飞行轨迹数据并进行轨迹分类预处理，通过模仿学习生成行为网络集作为原子行为集合，有效提高行为逼真度，并利用DQN 算法优化智能体策略探索能力。文献［24］提出SAIL 算法，通过将经验池中的优势轨迹数据扩充示例数据，提高算法收敛效率。

1.2 基于策略分布正则项的约束方法

上述基于示例的策略优化方法中，第3 类方法目前应用广泛，但基于行为克隆的预训练策略在与环境交互过程中存在复合误差，如果仅依靠强化学习算法在线细调，策略更新方向将不可控，例如，在飞行器机动控制时出现飞机不停滚转、坠地等情况，破坏预训练的初始化参数。这类情况下，学习率、batch size、更新次数等算法超参数设置不当可能直接导致算法无法收敛。因此示例数据应得到充分利用，在算法训练中对智能体策略更新方向加以约束。

在基于策略分布正则项的约束方法中，将示例数据保存在经验池DE中加以利用。设示例策略表示为πE，其状态-动作概率分布表示为dπE(s，a)，当前策略的状态-动作概率分布表示为dπθ(s，a)，πθ(s)即策略网络，根据输入状态s输出动作a。为衡量dπθ(s，a)与dπE(s，a)的相似性，采样(s，a)～DE，将二者分布距离作为策略损失函数的正则项，记为D(dπE(s，a)||dπθ(s，a))，其中D(·||·)表示概率分布空间的距离测量方法。因此策略优化方向约束为式（1），用κ衡量概率分布约束边界。

式（1）表示智能体策略在训练过程中的目标是在策略分布约束范围内，得到式（2）的最大期望回报Rπ，其中γ为折扣系数，确保无限长马尔科夫决策过程能够收敛。通过策略分布距离作为正则项，能够引导策略向示例策略方向收敛。

2 价值滤波

现实中真实对抗数据获得成本高，因此基于示例的策略优化方法的目标是充分利用少量的示例轨迹，结合在线训练来提高样本效率，但当示例数据质量低，如策略分布多峰或次优时，该方法难以得到最优解，会导致在线训练时的负向引导。因此基于次优示例的策略约束面临的难点在于如何对次优数据采样，从而接近最优策略π*。在上述预训练-在线细调的策略训练框架下，本文提出价值滤波，通过对优势经验数据和优势示例数据提取，提高算法收敛速度，并解决示例策略次优的问题。

2.1 价值函数滤波器设计

强化学习算法中优势动作评论（Advantage Actor Critic，A2C）、置信域策略优化（Trust Region Policy Optimization，TRPO）［25］、PPO［26］等在线策略（on-policy）算法，稳定性高，同时支持并行仿真，在计算资源充足的情况下具有优势，但on-policy 算法的采样机制导致经验数据利用率低；DQN、DDPG、TD3、SAC 等离线策略（offpolicy）算法［27］经验数据利用率高，为了提高有效样本的利用率，常采用优先经验回放等技术，但是当示例价值波动较大时，优先经验回放会提高次优数据的采样概率，从而降低价值网络的准确性，进而影响策略网络收敛性。为了解决上述问题，将基于策略梯度的在线策略算法和基于能量模型的离线策略算法相结合［28］，提出价值滤波方法。

基于策略梯度的强化学习算法训练的目标是接近最优策略π*，根据熵正则化强化学习和soft Q learning 理论［29］，最优动作价值函数和最优状态价值函数分别表示为

式中：Hπ表示策略的熵正则化，则推导出最优策略表示为

由式（5）可知，状态价值满足V*(st)≥Vφ(st)，即当前策略状态价值上界为最优策略π*的状态价值，因此必然有V*(st)≥Rt-，即当前策略下的回报小于最优状态价值。为了使当前策略快速逼近最优策略，训练过程增加优势样本的采样占比，选择Rt-＞Vφ(st)的优势数据进行增强训练，由此提出价值滤波器（V-Filter），定义为

式（6）在实现中忽略策略熵，文献［28］证明了当系数α很小时，状态价值函数将逼近最优状态价值函数的下界，说明价值滤波方法具有可收敛性。根据策略梯度算法得到利用回放经验的策略损失函数，即

式（7）直观表示算法训练中选择当前策略和状态价值评估下的优势状态-动作进行进一步模型训练。

2.2 基于价值滤波的策略约束算法

为了实现利用价值滤波对优势示例数据进行增强，提出基于价值滤波的示例策略约束算法（DPC）。为便于实现，首先将式（1）改写为拉格朗日函数形式［30］，即

该min-max 问题包含θ和η这2 个参数，为了降低算法设计和收敛难度，将η作为超参数，训练中仅更新策略网络参数θ，即

当奖励函数设计的目标与示例策略目标一致时，根据式（9），可以通过对基于策略（policybased）的强化学习算法优化，实现利用少量示例数据实现策略约束。

考虑到通过mini-batch 采样DE得到的策略分布dπE(s，a)存在较大误差，因此在策略约束算法具体实现中，算法参考行为克隆，采样示例状态-动作(，)～DE,～πE。因此式（9）简化为

针对实际示例数据中策略可能存在次优或不唯一的问题，将价值滤波与策略约束相结合，滤除采样示例数据中回报低于当前状态价值的非优势数据，仅对优势数据进行增强，因此式（10）改写为

针对可能存在的价值函数过估计问题，可利用广义优势估计（GAE）方法更新价值网络［31］，降低偏差和方差，价值网络损失函数表示为

注意到与优先经验回放不同，采样数据近似服从独立同分布，在训练初期，价值网络随机性较高，当其因过估计导致输出Vφ(st)＞V*(st)时，价值滤波器输出为0，即当前策略仅根据在线策略算法更新；当价值网络估计偏低时，策略同时由示例策略约束算法和在线策略算法更新；随着价值网络收敛，算法将对示例数据进行滤波从而解决示例次优问题。

2.3 PPO-DPC 算法流程

本文的DPC 算法可优化任意在线策略算法。以结合分布式PPO 算法为例，设置N个分布式Rollout Worker 和一个中心Learner。每个Worker 与环境交互并将四元组轨迹数据存放在各自的回合经验池（记为）中。回合结束后将数据存入全局回放经验池（记为Doff）中。

PPO-DPC 算法流程如算法1 所示，首先建立示例经验池，行为克隆生成预训练策略，并利用示例数据对价值网络进行初始化。由各Worker 与环境交互采集数据，回合结束后，将采样数据分割成mini-batch，策略梯度为

式中：ct(θ)表示当前策略和旧策略的概率比，即

将其回传Learner，由Learner 将各梯度累加并更新策略网络和价值网络参数，以上过程为近似在线策略训练过程。

每回合结束后，Learner 分别从Doff和DE中采样，根据式（12）计算策略梯度并更新策略网络。下一回合开始前，Learner 将更新的网络参数发布给各Worker，Worker 以新策略采样获得样本。

为了使智能体行为在训练初期能受示例策略约束，保证算法快速收敛，而训练中后期利用强化学习的环境探索能力进一步优化当前策略，式中参数η随训练步数增加逐渐降低。

3 实验系统设计

3.1 算法实验系统

本文算法实验系统框图如图1 所示。训练过程包含3 个阶段，

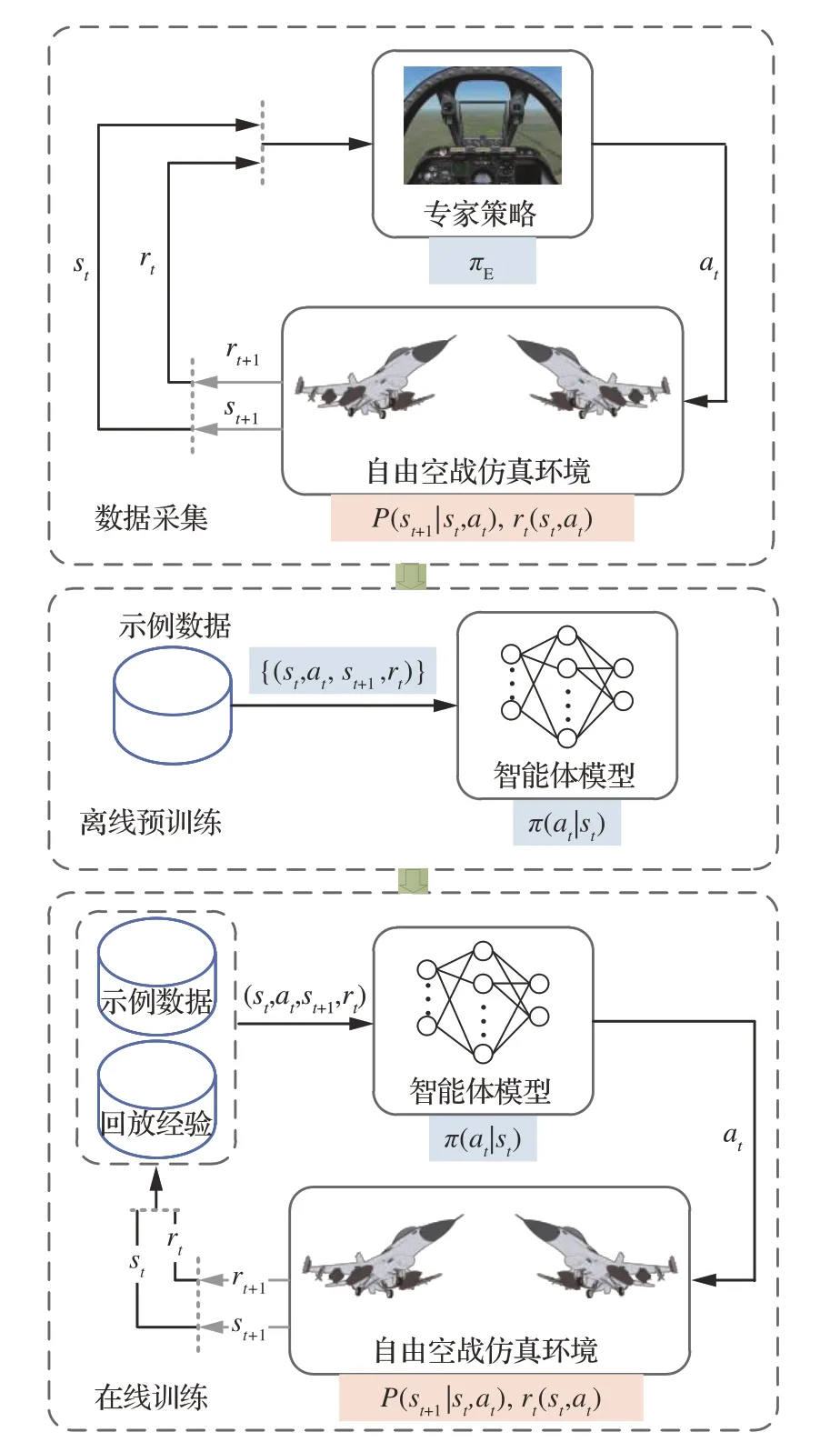
图1 实验系统框图Fig.1 Structure of experiment system

1）数据采集阶段：由专家策略模型与蓝方对抗生成对抗轨迹数据，即策略πE与环境交互，产生四元组(st，at，st+1，rt)，存入示例经验池。

2）离线预训练阶段：利用行为克隆初始化神经网络模型，提高初始阶段模型训练效率。

3）在线训练阶段：智能体与环境交互进行在线强化学习训练，提高智能体状态空间探索能力，解决行为克隆存在的策略偏移问题。

仿真环境中对抗双方采用相同的六自由度（6DOF）固定翼飞机模型。蓝方策略基于蒙特卡洛树搜索的层次化建模方法，决策层预测红蓝双方可到达位置点，并根据态势评估函数选择优势目标航点；控制层由PID 控制器控制飞机模型到达指定目标点。红方由基于神经网络的智能体控制。红蓝双方初始高度h∈[1，9] km，初始相对水平距离Δx∈[-10，10] km，Δy∈[-10，10] km，初始速度v∈[150，300] m/s，初始任意姿态。

3.2 模型输入输出变量设计

飞机的运动主要由发动机推力、升降舵、副翼、方向舵控制。当各操纵面变化时，模型根据对应的气动参数，改变飞机合力和合力矩。因此机动决策控制网络输出升降舵、副翼、方向舵和油门控制指令，实现飞机姿态和位置的控制，即

为了提高飞机控制的稳定性，飞机模型包含基于PID 控制器的稳定增强系统，包括角速度、过载反馈环路和控制指令前馈通路，控制器输出升降舵、副翼、方向舵偏转角度，分别表示为

对抗中考虑视距内格斗，同时具有预警机支援，双方态势透明，智能体模型输入状态st由自身状态和双方相对态势组成。其中自身状态表示为

其中：ψ、θ、φ分别表示航向角、俯仰角和滚转角；为俯仰角速度；表示当前滚转角；h表示归一化高度；V表示NED 坐标系下的归一化速度。相对态势表示为

其中：ΔV表示速度差；ΔX表示NED 坐标系下的相对位置；αATA表示方位角；αAA表示目标进入角。

3.3 奖励函数设计

奖励函数rt=r(st，at)是引导算法收敛的重要影响因素，本文奖励函数设计考虑角度优势、能量优势、自身稳定性等关键空战要素。

双方位置关系图如图2 所示，αATA和αAA用来判断角度优势［32］，相对欧式距离R用来引导我方接敌以到达格斗弹或航炮发射条件。因此，奖励函数rt设计为

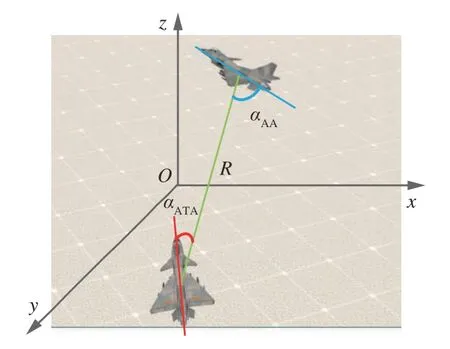
图2 相对位置关系图Fig.2 Diagram of relative position

其中：ηA、ηR、ηE分别代表的权重，本文中分别设置为0.5、0.3、0.2。

此外，当飞机飞行高度和飞行速度低于或高于阈值，引入惩罚项rpenalty，避免机动决策陷入快速‘死亡’等错误选择的局部最优。

4 系统仿真

本文强化学习训练环境采用OpenAI gym 平台，飞机动力学和运动学解算基于JSBSim 开源平台，飞机空气动力学模型为公开的F16 模型。

1）模型预训练阶段，由基于PID 控制器的简单策略模型对抗靶机目标，获取20 回合对抗数据，形成约2×105规模的示例数据集。基于该示例数据并对智能体策略网络和价值网络参数初始化。

2）模型在线训练阶段，仿真共2 200 回合，飞机状态仿真步长，即智能体决策间隔为20 ms，每回合最长时间5 min。算法中超参数设计如表1所示，策略网络和价值网络结构均采用全连接结构，其中隐藏层激活函数为均为ReLu 函数，策略网络输出层激活函数为tanh 函数。损失函数采用Adam 方法更新梯度［33］。

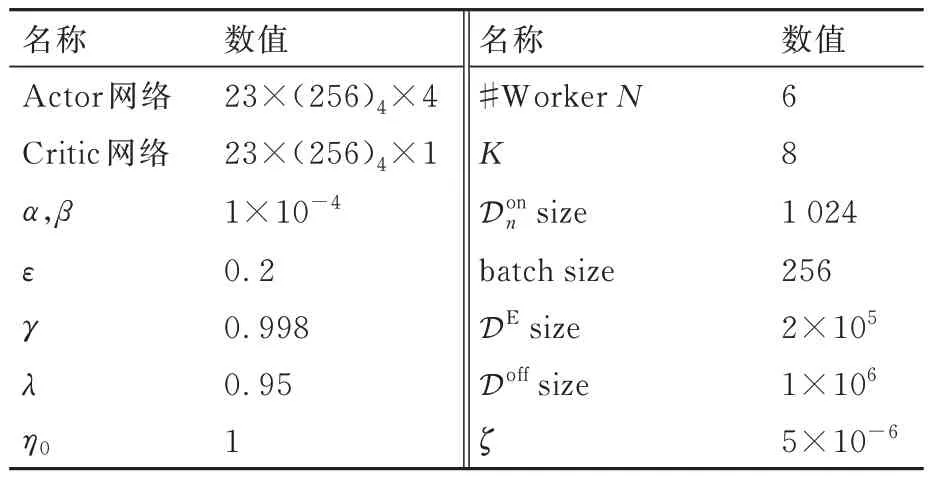
表1 PPO-DPC 算法参数设置Table 1 Parameters of PPO-DPC algorithm

回报函数的仿真曲线如图3，仿真对比了传统PPO 算法、PPO 算法结合自模仿学习［30］算法（PPO-SIL）、PPO 算法结合本文示例策略约束算法（图中PPO-DPC）、TD3-BC［34］算法（TD3-BC）以及BC 算法，其中BC 算法生成的模型作为上述4 种算法的预训练初始模型。结果显示利用专家数据的TD3-BC 算法和PPO-DPC 算法收敛速度明显高于PPO 算法，此外，PPO-DPC 算法通过优势经验数据的滤波，较TD3-BC 更快收敛。而PPO 与PPO-SIL 算法由于缺乏策略约束，态势观测发现智能体在训练中花费大量时间才能学会平稳飞行，因此回报函数上升缓慢。

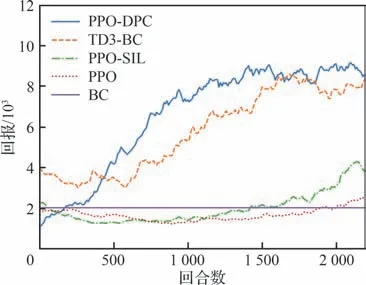
图3 回合回报仿真曲线Fig.3 Simulation of returns per episode

价值函数的仿真曲线如图4，仿真中设置γ=0.998，即价值网络估计约10 s 仿真步长的策略价值。为了衡量价值网络收敛情况，每次更新价值网络随机从DE中采样，估计示例策略价值，结果表明具有策略约束的算法，其价值网络在1×104仿真步数后基本收敛，能准确估计策略价值，而PPO-SIL 算法对状态价值估值较低。结合图3 回报函数曲线，说明策略约束能够辅助价值网络收敛，从而准确估计策略价值，在优化当前策略的同时有利于算法快速收敛。

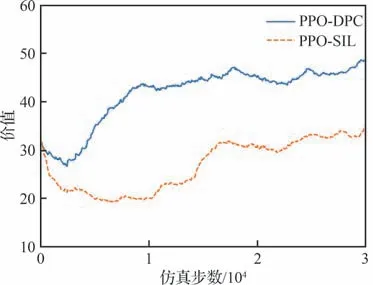
图4 价值函数仿真曲线Fig.4 Simulation of value function

示例利用率和动作误差仿真曲线如图5 所示。在训练初期，由于策略网络随机性较强，策略分布随机，此时示例数据利用率接近1，策略网络输出动作于示例动作误差较大；随着算法收敛，价值滤波器将采样示例的次优数据滤除，示例数据利用率逐渐降低为0.25 左右，同时动作误差在0.01 左右。结果表明在训练初期策略约束能够有效帮助策略收敛，后期利用价值滤波方法提高了智能体环境探索能力，从而避免示例策略次优的问题。

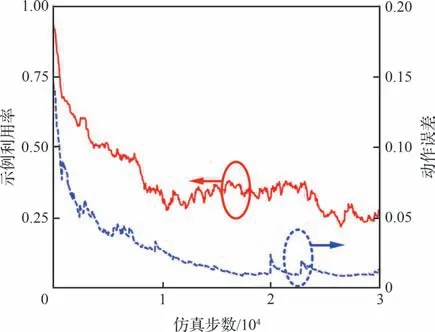
图5 示例利用率和动作误差仿真曲线Fig.5 Simulation of utilization of demonstration data and error of actions

图6 给出了博弈对抗的部分态势渲染图，从图中可以看到双方能够判断态势并做出合理的机动决策，完成如图中破S 机动、剪刀机动、筋斗等常用机动动作。

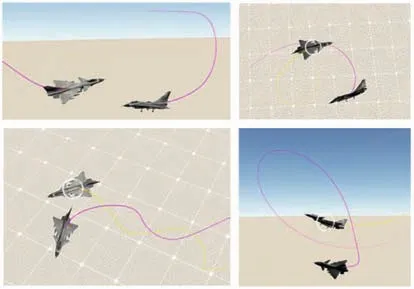
图6 博弈对抗场景渲染图Fig.6 Diagram of air-combat scene

为了验证基于DPC 算法的机动策略性能提高，图7（a）、图7（c）、图7（e）分别给出了示例策略、DPC 策略和PPO 策略对抗相同简单机动目标时的航迹，图7（b）、图7（d）、图7（f）分别对应其输出动作。航迹结果显示，示例策略在初始阶段能够调整跟踪目标，而90 s 后决策明显失误丢失目标；PPO 策略尽管始终保持相对距离，但未明显体现战术意图；相比之下DPC 策略能够始终占据蓝方后半球区域，保持角度优势和武器发射条件，更具智能性。通过输出动作曲线观察，DPC策略学习到示例策略的平稳变化规律，而PPO 策略抖动明显。结果证明DPC 方法能够模仿示例策略的同时，有效避免了示例策略次优的问题。

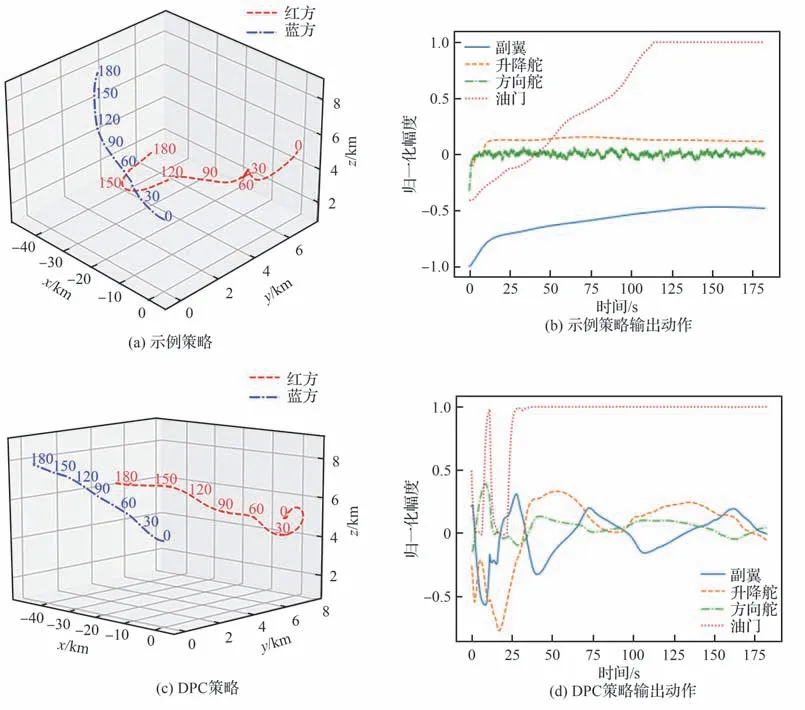
图7 相同目标下示例策略、DPC 策略和PPO 策略态势对比图Fig.7 Comparison of air-combat situation with the same target among demonstration，DPC and PPO based policies

为了验证机动策略的性能，图8 给出了使用本文生成策略的红方与蓝方简单靶机对抗的态势图。图8（a）初始条件为双方均势，航线相距4 km，相向飞行，红方选择高yo-yo 机动，而后迅速调转机头指向蓝方并保持优势位置；图8（b）初始条件为双方均势，航线相距4 km，同向飞行，红方连续压坡度转向蓝方，占据有利位置；图8（c）初始条件为双方均势迎头飞行，红方爬升规避，而后破S 机动转向蓝方后半球；图8（d）初始条件为蓝方位红方6 点钟方向，红方迅速急转，待蓝方无追击行为，转向蓝方。结果显示，红方反馈行为符合占据敌后半球优势位置的目标。

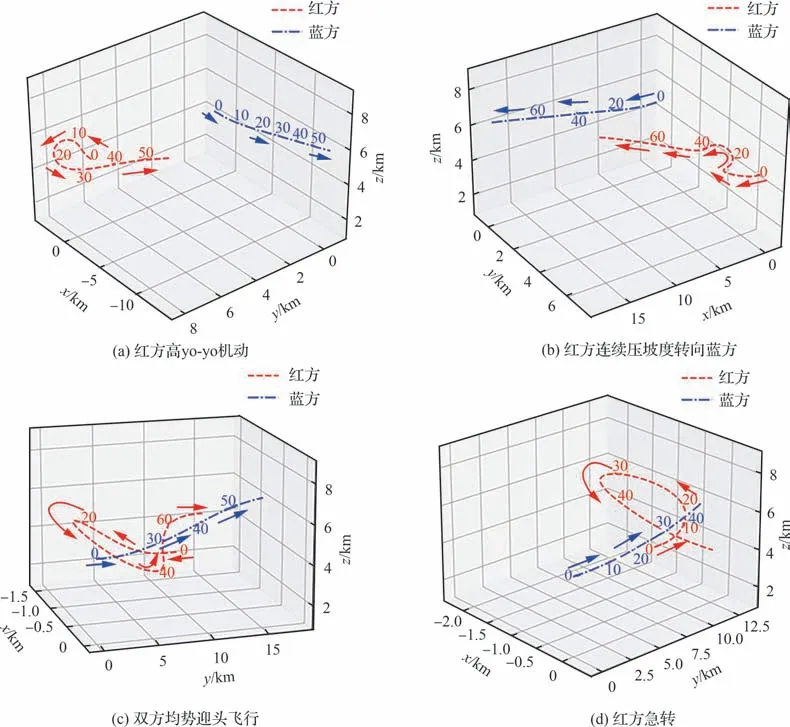
图8 简单目标对抗态势图Fig.8 Situation of combat with simple target

图9 给出了红蓝双发均使用本文生成策略的自博弈对抗态势图，图10 给出了策略网络输出动作，分别对应于图9 中红方智能体行为。图9（a）初始条件反向飞行，蓝方高度略高，具有能量优势，双方进入剪刀机动，红方逐渐陷入劣势，选择脱离，蓝方追击；图9（b）初始条件为红方略具角度优势，蓝方策略激进，选择急转接敌，而后双方进入单环战；图9（c）初始条件为蓝方占据角度优势和速度优势，红方急转规避，蓝方始终位红方后半球优势区域；图9（d）初始条件为双方均势，反向飞行，双方进入双环战。结果表明，在双方使用相同策略下，初始态势对于战局发展影响较大，与直观战术机动理解一致。对抗过程中，智能体能够利用副翼和方向舵协同转弯，并在大坡度机动时利用方向舵保持垂直高度，优于示例行为，同时配合使用油门和方向舵完成小半径转弯。通过上述比较分析，可以说明基于DPC 算法的机动决策模型具有一定智能性，能够判断态势并完成战术机动。

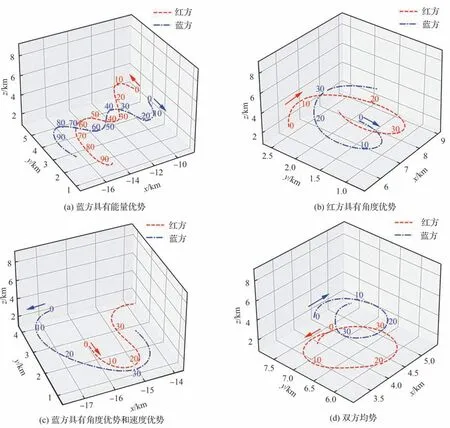
图9 自博弈对抗态势图Fig.9 Situation of combat with self-play

图10 策略网络输出动作Fig.10 Output action of policy network

为了验证智能体性能，基于VR 设备的桌面模拟器进行了人机对抗测试，如图11 所示，红方为人类，蓝方为智能体。智能体封装了简易火控雷达和武器模型，锁定目标后实时获取坐标、速度、姿态信息。图11（a）中蓝方为前述基于蒙特卡洛搜索树的简单智能体，图11（b）中蓝方为DPC 算法生成智能体。红蓝双方初始高度5 km，距离10 km，速度200 m/s，同向飞行。图11（a）智能体选择抵近飞行，被红方导弹锁定后未及时规避，迅速被击落；图11（a）智能体被红方跟踪后释放红外干扰并急转脱离，态势相对均势后进入近距缠斗，智能体能精确判断态势和控制机动行为，智能水平明显提高。

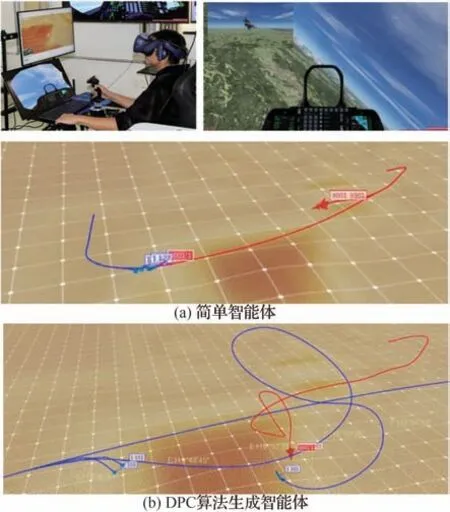
图11 人机对抗态势图Fig.11 Diagram of human-AI air combat

5 结论

针对近距空战智能体机动决策建模问题，提出并分析了价值滤波方法，提出了基于价值滤波的示例策略约束算法，DPC 算法通过价值滤波方法对优势示例数据进行学习，有效提高模型训练效率，同时避免示例数据的次优问题。

基于DPC 算法，建立了空战机动决策智能体建模流程，通过自博弈对抗和人机对抗实验，说明生成的智能体表现出较好智能性。为空战对抗训练中建立风格化智能陪练模型提供了新思路。