基于粒子群优化算法的风力发电机组选址规划

程 莉，雷 皓，孙文革

（新疆职业大学 机械电子工程学院，新疆 乌鲁木齐 830000）

电能已经成为当今经济社会发展最主要的动力之一，彻底融入人们的日常生活和各类生产活动之中。近年来，联合国以及各国之间达成共识，要降低能源消耗，减少环境污染。传统热力发电存在能源利用率低，污染严重等问题。为了达到节能减排、降低能耗的目的，分布式发电技术顺势而生。该技术具有低污染、高可靠性以及高持续性等优点，在市场中愈发具有竞争力。

分布式发电系统中较难解决的关键点是接入位置和接入容量的配置参数，二者配置不当会使分布式发电系统的能源利用率降低，导致系统的各项性能指标均达不到理想效果，甚至效果极差，从而造成系统不稳定。为了使分布式发电系统更高效和合理的运行，解决该系统最佳选址和最佳定容问题十分迫切。

一、风力发电机组

风是可再生能源之一，风力发电机主要利用风的动能，通过将动能转化为电能来进行发电。

（一）风力发电系统的基本结构

风力发电机的主要部件包括风速计、叶片、制动器、控制器、齿轮箱、发电机、高速轴、低速轴、机舱、桨距系统、转子、塔、风标、偏航驱动器、偏航电机等。

（二）风力发电机类型

根据叶片的不同类型将风力发电机进行分类，可将其分为水平轴风机和垂直轴风机两种。目前，垂直轴风机在市场上应用更为广泛。此外，由于应用场景不同，所需风机的结构类型以及配备电机的型号要求也不同。因此，根据转速的控制方式对风力发电机进行分类，可将其分为恒速恒频和变速恒频两种。

（三）电压暂降

电压暂降是指电力系统中某点的电压方均根值短时间下降然后恢复正常的一种现象。通常是由于极端天气、施工及人员误操作等意外原因所致。在我国，风力发电所产生的电能从生产端到消费需要跨越广阔的区域范围，在较长的输送距离中，不可避免地会受到不同地域环境、气候和海拔的影响，从而引起电压暂缓现象发生，因此风力发电机组的选址也成为解决此问题的一种办法。

二、粒子群优化算法

粒子群优化算法是一种基于群体搜索求解全局最优化问题的算法，其核心在于利用群体之中每个个体间的信息传递及共享找到最优解。

（一）粒子群优化算法基本原理

在粒子群算法中，群体中的每个粒子都存在着某种联系，信息能够在每个个体间进行传递，因此能够基于众多个体的决策找到最佳的解决方案。首先，对群体中的每个粒子进行初始化处理。在此过程中，最为关键的特征为粒子的位置，关键的节点为速度和适应度。其次，在确认最优方案时，通过最优粒子的特征参数来调整剩余的粒子参数让其趋近于最优值，实现整体的优化。在这种情况下，由于控制变量的参数范围会缩减到最小，因此粒子群也实现了整体的进化。

对于常见的非线性优化问题以及组合优化等问题，此算法能够令整体结构通过智能优化处理后在最短时间内达到最优解，优化效果极佳。如今，此算法已广泛应用于多个领域，取得了显著的效果。

（二）粒子群优化算法参数选择

本文所建立的粒子群算法是基于PSO 算法进行迭代更新的，因此合适的参数选取对该算法收敛的速度和准确性有着很大的影响。综合考虑二者，针对该算法的参数值选择及设定如图1所示。

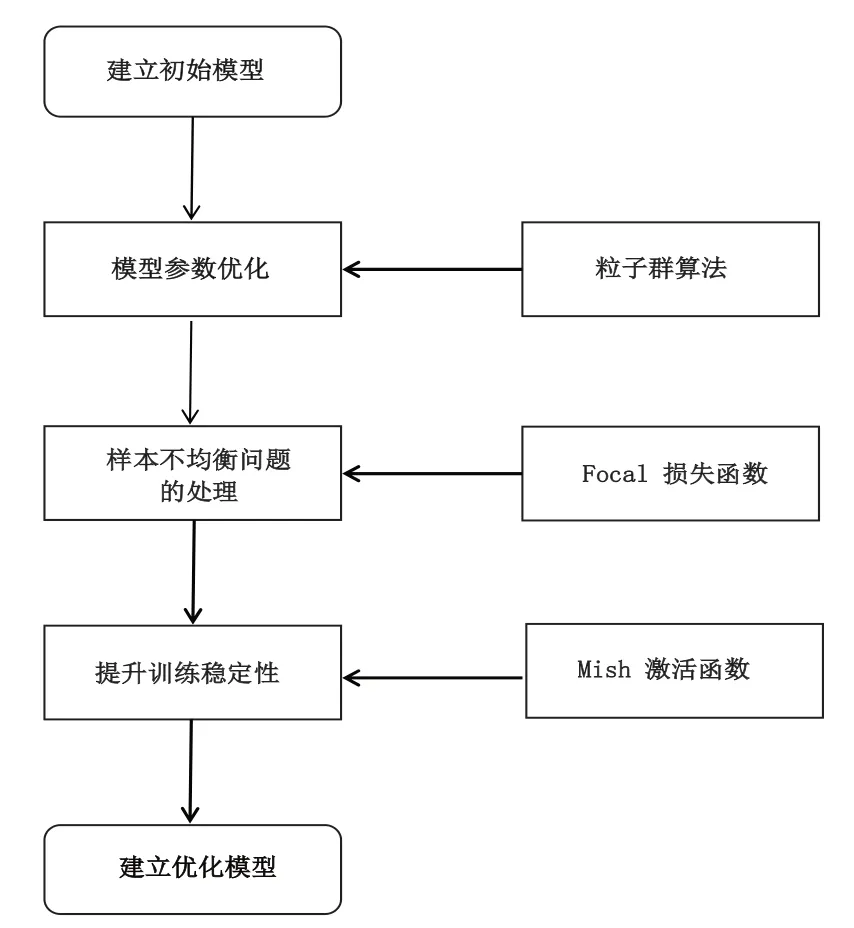
图1 粒子群优化算法流程示意图

1.种群粒子数量范围

PSO 优化算法的首要问题就是种群内粒子数量的设定，为了保证粒子在空间范围内具有足够的搜索能力，提高搜索效率，理论上应该将粒子的数量提高到足够多，但系统承载能力有限，无法在数据量过大的情况下依然保证整体的运行速度，所以根据经验设定种群初始的粒子数量为100 个。

2.惯性因子

根据郑州大学施俊等人的实验数据以及大量经验可知，随着粒子群体的不断迭代更新，其惯性因子也会逐渐降低活跃性，此时该算法的收敛特征逐渐显现，本文设定的惯性因子更新的表达式如下：

式中：ωmax——惯性因子达到最大值时的节点，ωmax——惯性因子达到最小值时的节点，T——进化次数，Tmax——群落更新的总次数。

调研对比多种类似实验数据的收敛特征，ω 的取值在不超过0.9 的范围内，该算法收敛效果最好。

3.学习因子

C1和C2为学习因子，通过不同的取值可改变粒子运行的尺度。C1和C2分别作为个体粒子和群体粒子最优位置的关键影响因素，其数值的选择一般要在1～4 的范围内，这样可以保证系统的粒子和粒子群在搜索过程中速度具备良好的变化趋势。

4.速度限制

粒子的搜索速度是影响系统输出结果和收敛速度的重要因素，速度过大，粒子在搜索时会产生飞跃，导致错过最优节点，无法获得最优解；相反，若粒子的搜索速度过小，虽然最终可以获得准确的最优解，但其收敛速度会大大降低，导致效率低，成本增加。所以粒子搜索的速度需要尽可能保证在合理区间内。

5.更新次数

更新次数的合理设定也会影响系统输出结果，当算法迭代到设定的最大更新测试时，系统会停止搜索。与速度限制相反，更新次数增加，则计算量增大，计算效率低，且输出结果的稳定性会下降；更新次数越小，结果的精确性就越低。因此根据经验，一般将群落的更新次数设定在100～500 次，这样无论问题复杂与否，都能保证输出结果有较好的效果。

三、基于粒子群优化算法的风力发电机组选址规划

（一）目标函数

本文主要解决的问题是风力发电机的定容选址优化，其影响因素包括风力发电机组的基本费用、电压暂降经济损失、电网网损经济损失、风能资源丰富性、容量系数和风向稳定性等，其中后三者是地理因素。本文所研究的问题是在特定地理位置的前提下进行的，地理因素对该问题的影响较小，本文不予考虑，假定该地区风速保持不变。选取风力发电机组的基本费用、电压暂降经济损失、电网网损经济损失作为风力发电机的定容选址优化问题的关键影响因素。

1.风力发电机组的基本费用

风力发电机组的基本费用组成应当从该系统的全寿命周期进行分析，囊括了该发电机组从设计、制造、安装、运行、维修、保养、废弃、回收等整个生命周期所消耗的成本之和，将经济性、可靠性等评价指标也都转换成等效费用。

f(Xi(t+1))是t+1 时刻粒子位置分量上的适应度函数，本文选取均方根误差函数作为适应度函数。

2.配电网的网络损耗经济损失

评价配电网在某一运行方式下的经济性能的重要指标就是网络损耗，而分布式电源合理布置接入可以在一定程度上降低配电网的网络损耗，从而提高电力输出能力以及配电网的经济性。结合上述分析和经验，本文选取的优化之一便是网络损耗经济损失。

该公式为群体最优值更新公式。该算法随机设置粒子的初始位置，之后利用PSO 算法迭代更新粒子的位置，通过计算粒子位置的适应度，判断粒子是否收敛到目标位置，得到最优解。

3.因电压暂降出现造成的敏感负荷经济损失

在某一特定接入方案下，在考虑多场景的影响后，调整敏感负荷电压暂降经济损失的计算公式。

式中，Vid(t)——当前时刻粒子的位置分量，Vid(t+1)——t+1 时刻的粒子速度。

（二）约束条件

1.电压变量不等式约束

所有节点电压必须满足以下条件：

2.支路电流约束

3.系统所安装的风力发电机组总容量

通常情况下，配电网的风力发电机总装机容量不能超过电网最大容量的10%～25%。

（三）算例分析

本研究中的风力发电机不同接入方案，主要是通过风力发电机组台数和接入点的变化进行设计的。配电系统中的IEEE33 节点有4 条母线可接入风力发电机，而每条母线最大又可接入8 台发电机，因此每条母线接入的风力发电机数在0～8 范围内随机取值，以此可计算出风力发电机接入方案共有153 000。

为了使评价优化后的粒子群算法的参数优化训练具有较好的效果，实验中粒子群优化方法选用PSO-Resnet 网络参数，同时使用ADAM 算法对其进行参数的优化训练和测试，迭代次数为400 次，其训练准确率曲线如图2所示。

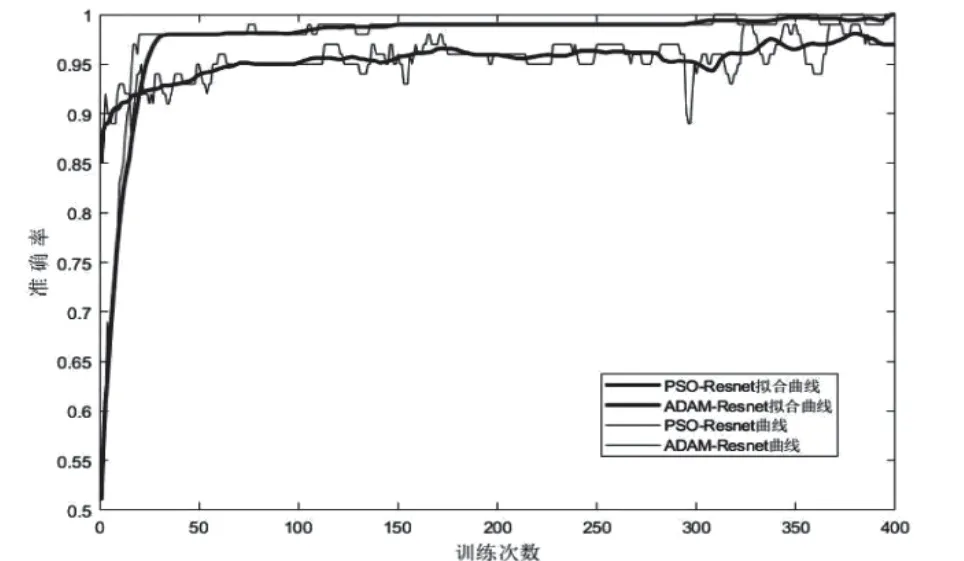
图2 训练准确度曲线示意图

本文为了验证上述PSO-Resnet 优化算法的故障诊断能力，将其结果和PSO-CNN 优化算法进行故障识别对比，经过400 次迭代更新后，两种优化后的PSO 算法的准确率曲线如图3所示。

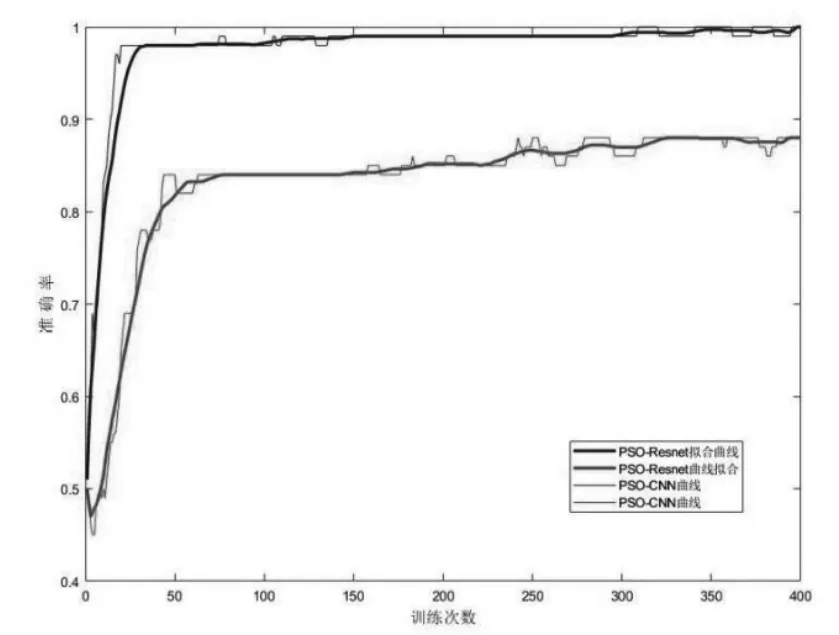
图3 训练准确度曲线示意图

为了更直观地观察对比以上三种优化算法的优劣，本文对三种算法进行了PCA 可视化分析，分别绘制出PSO-Resnet 网络、ADAM 优化的Resnet 网络和PSO-CNN 网络通过PCA 降维后的3D 特征图，如图4所示。通过对比三组特征可视化图像，结果表明，经过三种方法优化后的算法，虽然都完成了计算和记过输出，但是经过粒子群优化后的PSO-Resnet 网络模型不仅能够更为有效地提取样本特征，并且具备更高的诊断准确率，其特征的聚合效果也更好。

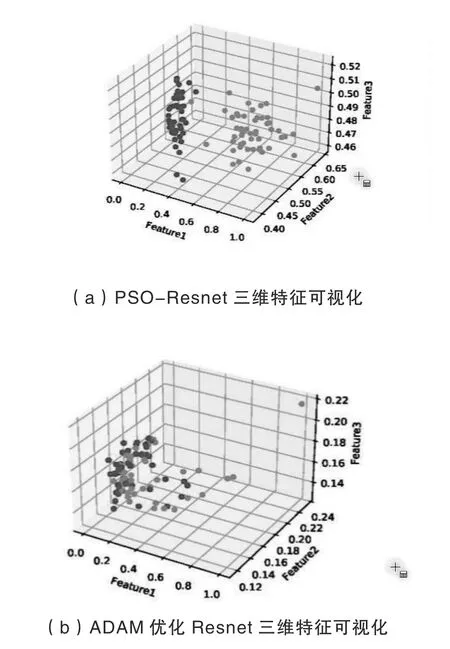
图4 特征参数可视化

四、结语

为了解决风力发电机组选址优化问题，本文基于粒子群优化算法建立了PSO-Resnet 网络，并与ADAM 优化的Resnet 网络和PSO-CNN 网络进行了实验对比验证，得到结论如下：

第一，在利用粒子群优化算法对PSOResnet 网络进行优化过程中，对模型中的阈值和权重进行了参数设定，提高了稳定性。

第二，通过PSO-Resnet 网络，可以有效解决不同类型和复杂程度的选址问题，并且可以根据具体的问题和复杂度进行自主优化。通过改变训练过程中的组数和网络的主体结构，可以提高模型训练的简易程度。

第三，通过PCA 可视化分析，将粒子群优化算法和PSO-Resnet 网络结合，具有更高的故障诊断准确率，并且通过实例分析优化网络，对风力发电机组选址问题实现了准确的预测和确定。