基于粘聚力单元的平整冰与海洋桩柱结构相互作用机理研究

俞同强，刘 昆，刘俊杰，王自力

（1.江苏科技大学船舶与海洋工程学院，江苏镇江 212003；2.中国船舶科学研究中心，江苏无锡 214082）

0 引 言

北极地区是一个冰封已久的宝藏，不仅蕴藏着丰富的石油、天然气等化石能源，还具有可观的风力、水、生物、土地、旅游等广义资源。随着全球气候变暖的加剧以及技术的进步，北极资源开发利用的难度不断降低，其巨大的经济和人文价值日益显现。极地海域广泛存在的漂浮平整冰是极地海洋装备面临的主要安全挑战，其巨大的推动力和产生的冰激振动往往会给海洋装备造成结构性损害，危及平台安全，与之相关的的事故屡见不鲜[1]。桩柱结构作为目前海上平台设施基座的基础结构，具有受波浪载荷作用小、结构连续性好的特点，得到了广泛应用，其在冰载荷下的结构性能也直接影响平台整体结构的安全性。因此，开展平整冰与海洋桩柱结构相互作用研究，探究结构的动态响应和海冰的破坏机理，对于评估冰载荷的大小和变化特点、提高结构性能、保障海上平台的安全性具有十分重要的意义。

海洋结构物与平整冰的相互作用机理一直是国内外学者关注的主要问题，也是冰区结构设计和疲劳寿命评估的重要依据。早期冰力的预报方法往往是基于试验的回归公式来计算最大静冰力，很多学者和各国规范也都给出了相关的计算公式[2]。然而，事实上，海冰的运动、挤压、破碎、重结晶等活动往往导致其动冰力显著大于静冰力，对冰激振动响应和疲劳寿命的评估已成为目前海冰研究的主要工作[3-4]。动态冰载荷问题是一个时域性的问题，在理论方法上进行全面研究目前仍有较大的困难。十九世纪七十年代，有学者提出了接触面冰材料非同时性破坏的特征[6]，即高压力区和低压力区交替出现，高压力区冰材料发生破碎和脱落。在此基础上，Jordaan 等[6-7]通过结构与平整冰的压缩试验，分析了平整冰在平面挤压作用下的破坏机理，建立了海冰与结构相互作用面内冰载荷高压区概率数学模型。

现场测试[8-9]和模型试验[10-11]被证明是研究海洋桩柱结构动冰力的有效方法，但是近年来数值仿真逐渐成为海洋结构物前期设计的重要辅助手段，其成本低、效率高、周期短的特点，在不同类型的结构-平整冰作用研究中均得到了广泛的应用[12-13]，同时随着计算机技术的迅猛发展，其准确性和适用性也在不断提高。但是，仿真分析中海冰材料的选择和仿真方法的确定是影响计算结果准确性和科学性的两个最为重要的问题。粘塑性、粘弹性、弹塑性以及泡沫材料等均被学者尝试应用于结构-冰碰撞的有限元仿真分析计算中[14-16]，在事故冰载荷的预报方面有较大的科学价值。但是传统有限元方法基于连续介质力学理论，使用单元强度模拟海冰强度，使用单元失效模拟海冰破碎的机制会导致失效单元的大量删除，既违背了守恒定理，也难以真实模拟海冰的碎裂、堆积等物理现象。

国内外学者也探索了很多具有创新性的仿真方法，其中以离散元方法、粘聚力单元、粘聚力接触、扩展有限元（XFEM）、自由网格法及分支裂纹阵模型等（wing crack model）[17-19]为代表的新型仿真方法近年来也得到了一定的尝试和应用，但距离成熟仍有一定的距离。可见，目前对于动态冰载荷的研究还没有一个达成共识的分析方法和理论，真正的动冰力计算还处于“初级阶段”。

考虑到海冰材料特征的复杂性与仿真方法的有效性，本文采用基于自定义材料本构和粘聚力单元相结合的仿真方法，将海冰的挤压和弯曲剪切破坏结合，建立平整冰-海洋桩柱结构的相互作用数值仿真模型并进行分析，重点关注相互作用过程中海冰的变形、失效以及冰载荷的时域特征，并对相关仿真参数影响进行一定的探讨。

1 基于自定义材料本构和粘聚力单元方法的平整冰仿真模型

如图1 所示，当平整冰遭遇直立/倾斜式海洋桩柱阻拦后，其主要发生的变形可分为三种：其一为平整冰自身发生挤压破坏，此时接触面边缘破碎脱落，而接触面中央的海冰在三维应力作用下则会显著强化；其二为平整冰的弯曲破坏，此时平整冰的破坏范围通常较大，破坏的海冰堆积于表面或沉入平整冰之下，桩柱前端形成敞水区，冰载荷大幅卸载直至下一次接触；其三为平整冰大范围整体开裂，此种破坏往往涉及到平整冰内部缺陷和大范围剪切载荷的传递，在本文中不予考虑。

图1 平整冰的几种破坏形式Fig.1 Damage modes of level ice

1.1 考虑接触界面挤压失效的海冰材料本构模型

在基本的海冰物理/力学参数测量之外，海冰的单轴和多轴试验是海冰强度测量最为重要的试验之一，其中海冰的多轴试验对于建立海冰的本构理论模型尤为重要，国内外很多学者都做了相关方面的工作[20-21]，其中Derradji-Aoua[22]通过总结归纳得出的多曲面屈服方程等到了广泛的接受和使用，该屈服方程可写为

基于上述屈服方程，建立相应弹塑性本构模型，本构模型在弹性阶段，应力应变关系满足各向同性广义胡克定律

式中：G为剪切弹性模量，G=E/2( 1+μ)；E和μ分别为弹性模量和泊松比；γj为工程切应变，γj=2εj(j=xy,yz,zx)；Δε0为静水应变增量，Δσ0为静水应力增量。在塑性阶段，由于屈服面的外凸性，塑性应变增量为

式中，dγ为塑性一致性参数增量，采用关联流动法则，总应变为弹性应变与塑性应变之和，可写作

式中：dσij为应力增量；δij为Kronecker符号，其值为0（i≠j）或1（i=j）。

当本构模型进入塑性阶段后，还需要对本构模型定义合理的失效准则。本文在冰材料本构模型中仅考虑海冰的挤压破坏，而不考虑海冰的弯曲或剪切破坏。这是由于当多种破坏形式共同存在时，往往会导致单元的提前失效并删除，其本质上是过高估计了海冰材料的抗剪强度，使挤压失效难以起到作用。本文基于Jordaan 的经验失效方程[6]，如式（7）所示，建立了以率无关和累积塑性应变为表征的动态失效准则来定义单元的失效，

积分率本构方程的数值算法，即应力更新算法，是通过本构方程计算与反馈应力状态的主要途径。本文采用Simo 等[23]提供的Cutting-Plane 算法来求解相关问题，首先计算测试应力σ和屈服判定，若屈服方程fyield( )p,J2＜0，则单元处于弹性阶段，测试应力σ即为真实应力，直接返回分应力值；否则，单元进入塑性阶段，进行塑性阶段内的迭代步计算，计算塑性参数Δγ并更新塑性迭代步内的应力值：

大型商用有限元软件ABAQUS提供了完整的用户子程序接口，依据上述分析选择VUMAT子程序编写海冰材料本构子程序，建立单元测试模型，单元底部约束，顶部施加恒定的压缩速度，单元四周施加恒定的围压，如图2所示。

图2 单元测试模型及载荷Fig.2 Single unit test model and load application

（1）输出J2-p曲线，如图3所示，可以看到，无论围压为0 MPa还是围压为0～100 MPa，在到达屈服点后（a、b 点），输出曲线和理论曲线完全重合，顶点坐标与理论解一致，有围压存在时，屈服点明显后移，可见屈服阶段的迭代计算收敛性较好。

图3 屈服方程理论曲线及输出值Fig.3 Theoretical and output value of yield equation

（2）围压为0 时，输出εf-p曲线，如图4 所示，可以看到，在单元到达失效点（c 点）之前，通过单元内部计算得到的失效应变曲线与理论失效应变曲线完全重合，而单元自身塑性应变在单元测试阶段通过两种方法求得，即通过塑性参数计算，以及通过总应变减去弹性应变的方法计算（εp=ε-εe），也取得了较好的一致性，可见在塑性阶段的失效计算是准确的。

图4 单元失效应变理论曲线及输出值Fig.4 Theoretical and output of failure strain

（3）考察阶梯变化围压下的失效应变值，其中围压分别为10～80 MPa，每隔10 MPa 为一个围压工况，所得结果如图5所示，可以看到，实际输出值与所设围压值有一定的偏移，表明静水应力和围压共同作用在实际的屈服和失效准则判定中。无论围压条件如何，失效时总应变均稍大于塑性应变，失效应变随围压的增大而减小，可见围压对于失效应变的影响是显著的。

图5 不同围压下的塑性失效应变值Fig.5 Plastic failure strain under different confining pressures

1.2 基于粘聚力单元的平整冰模型

粘聚力模型理论最早于上世纪60 年代提出[24]，目前主要被应用于混凝土及复合材料的研究中。本质上，粘聚力是原子或者分子之间的相互作用力，这种力客观存在，通过实际测量，定义合适的参数，可以有效分析界面损伤失效过程。在粘聚力区内，通常将裂纹面上各向应力定义为裂纹面上位移之间的关系，称为牵引力法则（Traction Separation Law，TSL），可写作

开裂过程中释放的能量定义为断裂能，可写作

牵引力法则分为三个阶段，第一阶段为初始损伤之前的弹性阶段，此时应力应变线性增长；第二阶段为损伤之后的软化阶段，此时单元刚度随损伤的发展逐渐降低；第三阶段为到达最大分离值时，单元删除。可见，粘聚力模型有两个重要材料参数，分别为最大粘聚力值与断裂能，这两个参数均为材料常数，其大小取决于材料的破坏强度及粘聚力区域的尺寸。

在几何方面，理想粘聚力模型一般采用厚度为0的粘聚力单元来表示，但也可采用厚度值极小的单元来替代，如图6所示。有限元软件ABAQUS 提供了粘聚力单元功能，定义双线性软化粘聚力模型本构，其牵引力法则曲线如图7 所示，该本构模型不可逆，可以看作是塑性区裂纹积累所导致的材料软化现象。此外粘聚单元不代表任何物理材料，仅描述了发生断裂时的粘聚力，在仿真中即使单元厚度不为0，其质量也应当设为0，因此粘聚力单元的侵蚀不违反守恒定律。

图6 粘聚力单元图Fig.6 Cohesive element

图7 双线性软化粘聚力模型本构Fig.7 Constitutive model of bilinear softening cohesive element

参考相关文献资料[25]，确定输入参数开展基本模型测试验证，如表1所示。

表1 粘聚力单元材料参数设置Tab.1 Material parameters of cohesive element

建立基本三单元测试模型，其中中间是厚度为0 的粘聚力单元，分别施加恒定的压缩与拉伸速度，考察单元失效形式，如图8 所示。可以看到，在压缩载荷下，随着挤压作用的增强，冰体单元应力不断上升，冰体单元达到失效准则后单元失效，此时单元删除，单元应力为10 MPa左右。当载荷为拉伸载荷时，粘聚力单元达到失效准则后删除，有限元单元保留，单元应力约为2 MPa左右，与设置的参数吻合，可见应力状态是合理的。

粘聚力单元的使用本质上是一种唯像的方法，理论上粘聚力单元的分布形式很大程度上限制了裂纹的扩展路径。Turon 等[26]指出，在粘聚区任意方向上至少需要三个网格才能满足预测裂纹扩展的要求，对于各向同性多年冰以及横观各向同性一年冰，其结晶方向由表层向上进行，因此采用正交分布的粘聚力单元是合理的。同时，冰单元的应力状态也和网格尺寸有直接联系，参照文献[27]的方法进行网格敏感性研究，将1 m×1 m×1 m的立方体划分为不同的网格大小并嵌入粘聚力单元，施加相同的压缩载荷，观察冰单元应力状态的变化。结果表明，单元尺寸越小，单元的应力越大，当单元尺寸小于0.14 时，单元应力有明显的收敛值（见图9 所示）。在实际计算中，还应根据计算时间的成本进行综合考虑和试算，确定合理的网格大小。

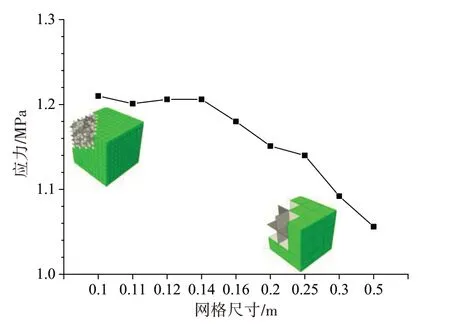
图9 网格收敛性验证Fig.9 Mesh convergence verification

2 平整冰与海洋桩柱结构相互作用机理研究

2.1 试验及仿真模型

基于上述自定义本构和粘聚力单元相结合的方法，建立平整冰与桩柱结构相互作用的仿真分析模型，仿真模拟工况参考武海斌等[28]在天津大学冰水池开展的单桩风机基础与冰层作用的模型试验，针对3 MW 单桩风机的试验结果进行仿真验证。模型试验所模拟的冰况为冰厚40 cm，挤压强度2.06 MPa，冰速范围0.05～1.2 m/s，缩尺比λ=20。由于粘聚力单元中有关模型冰的参数，尤其是断裂能等难以获得，而实尺度下有国外相关的测量结果，因此本文建立实尺度工况下的数值模型以保证输入参数的科学性。综合考虑计算时间等因素，实尺度下仿真模型的相关参数如表2所示。仿真分析模型如图10 所示，其中桩柱结构采用壳单元建模（S4R），网格大小为0.1 m，材料为刚体，不考虑其变形，且约束除运动方向外的其他自由度。平整冰采用实体六面体单元建模（C3D8R），网格大小为0.1 m，材料属性为用户自定义材料，基本材料参数如表3 所示，平整冰除接触面外其他三个面边缘节点约束所有自由度。粘聚力单元为0厚度体单元（COH3D8），材料参数仍如表1所列，接触摩擦系数为0.15，粘聚力单元粘性系数设置为0.0001，以增强收敛性，采用36核主频2.24 GHz工作机计算200 s耗时约320小时左右。

表2 实尺度下仿真模型相关参数Tab.2 Parameters of simulation model in full scale

表3 平整冰单元基本材料参数Tab.3 Material parameters of leveling ice

图10 仿真分析模型与网格特征Fig.10 Simulation analysis model and mesh characteristics

2.2 仿真结果对比与分析

针对3 MW 风机桩柱在平均水位破冰速度为0.05 m/s工况进行了仿真对比研究，该工况对应于低速工况。

当实际相对速度为0.05 m/s，即试验相对速度为0.011 m/s时，图11给出了仿真和试验中海冰破坏的对比图。可以看到，海冰的局部挤压和小范围压屈破坏在仿真和试验中均有体现，试验中小范围压屈以环状裂纹的形式扩展，但在仿真中以规整的单元断裂为特征，这主要受到有限元网格划分形式的影响。图12给出了仿真和试验中的时程接触力图，可以看到仿真和试验中的接触力曲线总体特征基本吻合，峰值力均在400 N 左右。两者的接触力平均值分别为86 N和91 N，仿真值略小于试验值。在小范围压屈阶段（图中A 段）接触力呈现整体加载—快速波动—整体卸载的变化轨迹，并在其后有一个较长时间的准空载阶段，可见在发生小范围压屈时，存在块状海冰非同时破坏的现象。在局部挤压阶段，接触力总体呈现震荡上升到达峰值力后震荡下降的趋势，总体来说，小范围压屈破坏所占比例相对较小，平整冰主要发生的还是挤压破坏，这点在仿真和试验中是一致的。但是，由于平整冰碎裂和破坏的随机性，时程接触力的局部特征难以吻合，试验中除初始阶段外没有整体屈曲破坏发生，但是在仿真中这种破坏形式在整个作用过程中均有出现（图中B段），且试验中测量值的震荡幅度较大，这在仿真后半段时间内才有一定的体现。

图11 速度为0.011 m/s时平整冰破碎情况Fig.11 Breaking condition of level ice at a velocity of 0.011 m/s

图12 速度为0.011 m/s时接触力时程曲线Fig.12 Time history of contact force at a velocity of 0.011 m/s

2.3 参数敏感性

针对3 MW 风机桩柱在平均水位破冰速度为0.6 m/s 和1.2 m/s（即试验相对速度为0.134 m/s 和0.268 m/s）两个工况进行仿真对比研究，对应于中高冰速工况。

图13 和图14 分别为两种工况下仿真和试验中平整冰破坏的对比图和接触力时程曲线。可以看到相对速度较大时，平整冰局部挤压和小范围压屈破坏两种破坏形式同时存在的特征并没有发生变化，单元最大应力为8～10 MPa 左右，应力水平随速度的提升有一定的增强。此时试验中平整冰屈曲破坏的范围大幅减小，同时有小尺寸碎块产生，这种趋势随着速度的增大而越发明显；仿真中则表现为平整冰的破坏更加碎片化，碎片的飞溅也更加严重，海冰的弯曲变形更为明显，但海冰的屈曲破坏仍然存在并占据一定的比例。从时程接触力的对比来看，两种形式破坏的接触力特征区别已不明显，除初始阶段外接触力曲线没有显著的卸载段出现，总体上接触力表现为在一定幅值内反复震荡的特征，伴随有规律性的个别较大峰值的出现。试验和仿真结果都表明，速度的变化不是影响峰值接触力大小的主要原因，无论是仿真还是试验，速度增大24倍，但是峰值力的大小没有显著的变化，均维持在300～400 N 左右，但是速度的变化显著改变了接触力的平均值和时域变化特征，速度越大，平均力越大，同时规律性的振荡也越明显，接触力振荡的频率以及峰值碰撞力出现的频率均显著提高，其往往是引起冰激共振、造成结构损坏的主要原因。

图13 速度为0.134 m/s和0.268 m/s时平整冰破碎情况Fig.13 Breaking condition of level ice at velocities of 0.134 m/s and 0.268 m/s

图14 速度为0.134 m/s和0.268 m/s时接触力时程曲线Fig.14 Time histories of contact forces at velocitise of 0.134 m/s and 0.268 m/s

标记桩柱运动过程中失效的平整冰和粘聚力单元，记录桩柱位移分别为2 m、4 m、6 m、8 m时各类型单元的失效数量和粘聚力失效单元所占的百分比，如图15 所示，其中粘聚力单元和冰单元原始数量分别为131 120 和48 000 个。可以看到，失效单元的总数随桩柱运动距离和速度的增加而呈近似线性增加的趋势。从各类型单元失效占比来看，随着运动的进行，粘聚力失效单元占比均表现为逐渐下降的趋势，同时随速度的增大而逐渐减小。这主要是由于速度较大时，冰单元往往难以形成稳定的围压状态，导致其更易失效。不同工况下，粘聚力失效单元数量占比均在95%以上，可见由粘聚力单元引起的弯曲剪切失效仍是主要的失效模式。同时需要指出的是，粘聚力单元的基数约三倍于冰单元数量，这也是造成粘聚力单元失效数量占比较大的一个重要原因。

图15 失效单元数量与粘聚力失效单元占比Fig.15 Number of failure elements and proportion of cohesive failure elements

考察圆台桩柱倾角对于平整冰失效特性的影响，在原型桩柱尺寸的基础上，改变圆台上底直径至200 mm、150 mm、100 mm、50 mm，下底直径不变，即倾角分别为86°、84°、82°、80°，平整冰的破碎情况及接触力时程曲线如图16 和图17 所示，失效单元数量及计算得到的粘聚力失效单元占比如图18 所示。可以看到，由于角度变化较小，不同倾角下平整冰的破碎特征没有显著的差异，倾角较大时，整体破碎的现象较为明显，冰单元应力大小与典型工况基本相同，均维持在8 MPa左右。时程接触力非线性、多峰值的特征没有发生改变，总体上峰值接触力随倾角的增大而呈非线性减小的趋势，第一个峰值力大小分别为343.73 N、258.71 N、207.60 N和167.34 N。稳定破冰后前三种工况接触力的峰值差异不明显，倾角为80°时峰值接触力明显减小，同时，接触力波动频率和峰值接触力出现的频率也基本相同。平均接触力随倾角的增大变化明显，平均力从倾角为86°时的76 N下降到倾角为80°时的54 N左右。从失效单元数量和比例上来看，总体上，失效单元数量随倾角的增大而逐渐减小，在单个工况中失效单元数量随移动距离呈现线性特征，粘聚力单元失效比例不断降低，总体占比在85%～90%左右，由于各工况倾角仅有2°的变化值，可见粘聚力单元的失效对于倾角的变化是十分敏感的。

图16 不同倾角下平整冰破碎情况Fig.16 Breaking condition of level ice at different inclination angles

图17 不同倾角下接触力时程曲线Fig.17 Time history of contact force at different inclination angles

图18 不同倾角下失效单元数量与粘聚力失效单元占比Fig.18 Number of failure elements and proportion of cohesive failure elements at different inclination angles

考察圆台桩柱接触部分直径对于平整冰失效特性的影响，在原型桩柱尺寸的基础上，改变圆台下底直径至250 mm、200 mm、150 mm、100 mm，上底直径按照比例改变，此时倾角不变，为87°，平整冰的破碎情况和接触力时程曲线如图19和图20所示，失效单元数量及计算得到的粘聚力失效单元占比如图21 所示。可以看到，平整冰的破坏形式随桩柱直径的减小显著不同，但是整体上屈曲失效和破碎失效同时存在的特征没有发生改变，单元应力有小幅减小，下底直径为100 mm 时单元最大应力减小为8.26 MPa左右，但是总体应力水平仍在8 MPa左右。在时程接触力上，第一峰值力分别为376.12 N、352 N、342.92 N和246.0 1N，呈非线性下降的趋势，这种趋势在第二个峰值力体现得更为明显，第二峰值力在下底直径为250 mm 时为327.21 N，而在下底直径为200 mm时大幅降低至202.66 N。接触力的平均值也呈非线性减小的趋势，四种工况下接触力平均值分别为76.43 N、59.39 N、51.91 N、40.57 N。接触力峰值出现的频率随直径的减小有一定程度的提高，这主要是由于直径较小时，圆柱面弧度增大，冰单元更易向两侧挤出，增加了撞击几率。由图21 可以看到，随着桩柱直径的减小，无论是冰体单元还是粘聚力单元，失效单元的数量均显著减少，粘聚力失效单元占比也逐渐降低，但总体占比仍在85%～90%左右，可见粘聚力单元的失效在平整冰整体失效破碎中起着十分重要的作用。

图19 不同直径下平整冰破碎情况Fig.19 Breaking condition of level ice under different diameters

图20 不同直径下接触力时程曲线Fig.20 Time histories of contact forces under different diameters

图21 不同直径下失效单元数量与粘聚力失效单元占比Fig.21 Number of failure elements and proportion of cohesive failure elements under different diameters

综上可见，桩柱的倾角和直径显著影响平整冰的破坏和失效特征，但是屈曲破坏和挤压破碎同时存在，且非同时性破坏特征明显的情况没有改变。应力水平在不同工况下有规律性地变化，总体在8～10 MPa左右，可见在冰体受到挤压时考虑围压的影响是十分必要的。失效单元随速度、直径的增加和倾角的减小而增加，粘聚力和平整冰单元同时存在失效，无论何种工况，粘聚力失效单元比例随桩柱的运动距离逐渐降低，但是粘聚力失效单元占主要多数的情况没有发生显著变化，总的比例均维持在85%以上。

3 结 论

本文基于自定义材料本构和粘聚力单元相结合的方法，建立了平整冰与海洋桩柱相互作用的数值仿真模型，深入分析了平整冰在与桩柱作用过程中平整冰的破坏特点和时程接触力的变化特征，探究了速度、倾角和直径的影响规律，得到如下结论：

（1）通过自定义材料本构和粘聚力单元相结合的方法，将平整冰的挤压破坏和弯曲破坏分开对待，解决了传统有限元软件难以模拟碎冰的问题。通过单元验证工作，验证了子程序的执行正确性，同时通过简单的粘聚力测试模型，阐述了粘聚力的作用机理和网格的收敛性特征。

（2）仿真结果表明，本文所提出的仿真方法能够有效地模拟平整冰与桩柱相互作用时平整冰的破坏特征及接触力的变化情况，尤其是局部挤压和小范围压屈破坏的破坏特征在仿真中均得到了合理的反映。

（3）不同工况下平整冰破碎的特征基本相同，屈曲破坏和挤压破碎同时存在，且非同时性特征明显。粘聚力和平整冰单元同时存在失效，失效单元随速度、直径的增加和倾角的减小而增加。无论是仿真还是所参考的试验结果均表明，速度的变化对于接触力峰值的大小没有明显影响，但会显著改变接触力的平均值和时域变化特征，主要表现为规律性的振荡和峰值，其往往会引起冰激共振，造成结构疲劳损伤，带来安全风险。

需要指出的是，由于海冰的挤压破碎现象和粘聚力客观存在，本文提出的仿真方法具有较强的实用性和科学性，同时考虑到一年生平整冰表现为各向异性，通过给横向和竖向粘聚力单元施加不同的材料属性能够模拟这一特征，结合自定义材料本构的可拓展性优势，这一仿真方法在未来的科学研究中也具有较广的应用前景。