土拱对复合桩支护基坑性能的影响研究
孙春娥,彭真,方莉 (中建二局第二建筑工程有限公司,广东 深圳 518000)
0 引言
近年来,随着地铁、高层建筑、矿山等工程的快速发展,,土拱效应的研究也越来越被重视。众多学者对土拱效应进行了广泛的研究,李世忠等[1]通过数值模拟,研究了柔性挡土墙对邻近深基坑的影响。研究发现,当土拱效应发生时,侧向土压力将被重新分配。王刚等[2]人采用有限元数值模拟方法,研究列车荷载作用下路堤土拱效应。结果表明,桩身模量和摩擦角对土拱效应有显著影响。赵杰等[3]提出了一种基于极限平衡理论方法计算端承土拱和摩擦土拱的合理桩间距方法。
上述研究多从桩的不同种类研究土拱效应。然而,目前针对复合桩结构支护基坑的土拱效应相关研究较少,且复合桩支护基坑时,由于基坑开挖[4],桩被侧向土压力推动,使土颗粒水平移动,形成水平土拱。而基坑发生土拱效应会使基坑侧壁发生滑塌,对基坑施工安全带来严重影响。基于此,本文利用PFC2D二维离散元软件,研究复合桩结构支护基坑在开挖过程中对水平土拱的影响;研究不同桩直径、桩位置和摩擦系数对土拱形状和土体颗粒总位移的影响。
1 工程概况
某建筑地库拟建场地位于我国东南地区。地库基地标高7.16m,开挖上口尺寸为107.75m×67.75m,开挖基低下口尺寸为94.65m×54.65m。施工现场基坑提供临时支护,基坑深度为9m。除表层回填外,土层主要为粉质粘土。土壤具有较低的抗剪强度,较大的孔隙度和流变特性,且含水量大。该土层的开挖对墙体及周边土体的稳定性影响较大。但由于基坑两侧土质不一样,为降低工程造价,钢管桩与混凝土桩联合使用用于该工程基坑支护,但在实际施工时,发现基坑坑底出现土拱现象,土体在压力作用下发生位移形成土拱,进而改变土体的应力状态,使土体应力重新分布,严重影响基坑安全。因此,分析复合桩结构支护基坑时的土拱效应,对于基坑施工安全尤为重要。
2 模型建立
根据施工现场布置图,建立数值模型。图1 为桩支撑基坑的正面视图。桩号1、3、5 为钢管桩,桩号2、4 为混凝土桩。数值模型尺寸设定为2m×1m,混凝土桩直径d=0.4m,钢管桩直径D=0.5×d,桩间距L=1.25×D=0.5m。本文设定三种桩位置情况,即钢管桩与混凝土桩顶部在一条线上,钢管桩与混凝土桩中心在一条线上,钢管桩与混凝土桩底部在一条线上,进一步研究不同桩位置对土拱效应的影响。在模拟过程中,设定钢管桩和混凝土桩不发生位移,但桩顶或桩身在实际工程中会发生微小位移。因此设定模型左右两侧墙体固定,桩固定。通过上部单元的慢位移模拟土体的运动,观察桩对基坑产生的水平土拱效应。设定上部单元以1mm/s 的速度移动,加载方向向下,加载持续时间为100s。本文模拟的土为粉质粘土,模型中土壤颗粒的粒径范围为0.2~2mm。土壤颗粒为中粗砂,由多层压实法,土壤颗粒总数为18385个。粉质粘土的接触模型为线性模型。
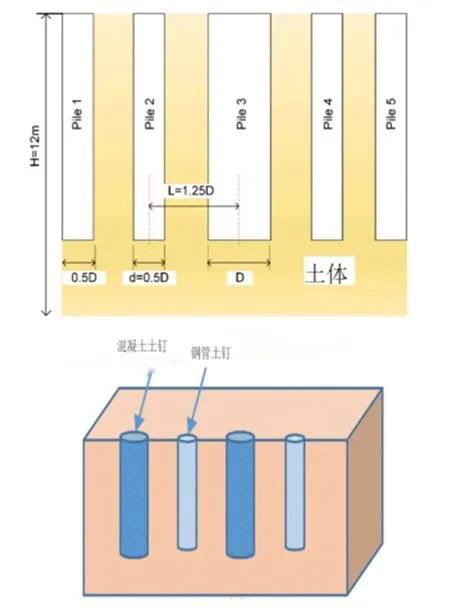
图1 桩支撑基坑示意图
3 桩对土拱效应的影响
3.1 不同桩直径对土拱效应的影响
为了更直观地分析桩直径对某建筑地库基坑土体产生应力拱的影响,采用第二应力张量不变量I2来表示土体应力拱[5]。I2表示剪应力状态。Mises 等效应力与I2直接相关σ=0.3I2。因此,利用Mises 屈服准则,I2可以用来评价应力点的破坏状态,利用测量圆可以得到数值模型的I2。在第二应力张量不变云图中,第二应力张量不变量最长的方向与主应力最大的方向相对应。因此,第二个应力张量不变量(I2)的公式为:
图2 为混凝土桩顶与钢管桩顶对齐,上部单元移动100mm 时,桩顶部土体I2云图。当上部单元向桩移动时,会对土颗粒施加荷载(模拟侧土压力),这将导致模型中土颗粒的应力重新分布。桩顶会形成应力拱。图2(a)中的应力拱呈抛物线形状。随着2 号桩和4 号桩的桩径减小,形成不同直径的复合桩。图1(b)、图1(c)和图1(d)中的应力拱呈半椭圆形。由图1 可知,桩直径减小,即桩间净距Δs=L-(d+D)/2 增大,土颗粒应力重分布空间也增大,I2进而减小。

图2 不同直径桩I2云图和土拱形状
图2为不同桩直径下沿不同断面土体竖向位移变化。从图中可以看出,当桩的直径减小时,桩之间的净距离越大,土壤颗粒的竖向位移将越小,因为更多的土壤颗粒被移动以抵抗土体上表面施加的荷载。随着切割表面位置上升,y=-0.3m、-0.2m、-0.1m 和0m 时,土壤颗粒的竖向位移持续减小。同时可观察到土体颗粒的最大位移出现在两个桩的中间。这种情况与Van Eekelen 等描述的加固桩支撑路堤的两个桩之间的位移趋势一致,且随着桩直径的减小,土体竖向位移由三角形变为拱形,并呈对称分布[6]。
图2(a)为钢管桩d=D情况下土粒垂直位移曲线。当钢管桩直径与混凝土桩直径相同时,桩间净距离最小。因此,土体的垂直位移最大,这意味着由于土体没有约束,大量的土颗粒在桩间被挤出,其最大值为282mm。图2(a)中的黑色曲线和红色曲线不是连续的,主要由于y=-0.3m 和y=-0.2m 时,2 号桩、3号桩和4号桩处没有土颗粒。
图2(b)中桩底部的土体颗粒不受竖向力。因此,在图2(b)中,桩底部土壤颗粒的竖向力位移趋于0。
且图2(c)中,截面y=-0.2m 与桩底完全在同一水平线上,这与图2(b)中截面y=-0.3m 处土粒受力情况一致。因此,在图2(c)中,混凝土桩底部土体竖向位移也趋于0。
如图3 所示,当钢管桩直径继续减小时,土颗粒的最大位移也随之减小。同一截面内,两桩中间的土体竖向位移最大,且越靠近桩心,土体竖向位移越小。在y=-0.1m 和y=0m 截面处,土体位于桩顶,土体竖向位移与上部单元位移大致相同,约为100mm。随着y=-0.3m 断面向上移动到y=0m 断面时,土体竖向位移逐渐减小[7]。土体距桩越远,土体竖向位移波动也越小。且通过分析不同桩直径对土拱效应的影响,发现随着桩直径的减小,钢管桩与混凝土桩之间的土体位移拱由三角形演化为塔形,最后演化为拱形。土拱效应是基坑支护研究的一个重要方面,它与桩的支护效果有关。因此对于实际工程支护基坑,减小桩直径可以降低工程造价。

图3 不同小桩径下土壤颗粒沿不同截面的垂直位移曲线(d=D(情况a);d=0.5D(情况b);d=0.25D(情况c);d=0.2D(情况d))
图4为桩间距为1.25D 时土颗粒位移云图,桩直径分别为d/D=1、d/D=0.5、d/D=0.25、d/D=0.2。如图3(a)所示,当混凝土桩直径与钢管桩直径之比为d/D=1 时,桩间土粒位移大致相同,呈三角形。当上部单元移动100mm 时,土壤颗粒的最大位移为375mm。之所以会出现这么大的位移,是因为底部边界处的土壤颗粒没有受到约束。实际中存在喷射混凝土层,位移相对较小。该模拟主要是为了揭示土拱的机理。由图3(b)~图3(d)可以看出,随着桩直径d/D的减小,桩间净距离Δs=L-(d+D)/2增大,土壤颗粒的自我重组空间增大,导致土壤颗粒的最大位移比例减少。此外,还可以观察到,随着混凝土桩直径的减小,混凝土桩和钢管桩之间的土颗粒位移土拱由三角形向塔形转变。
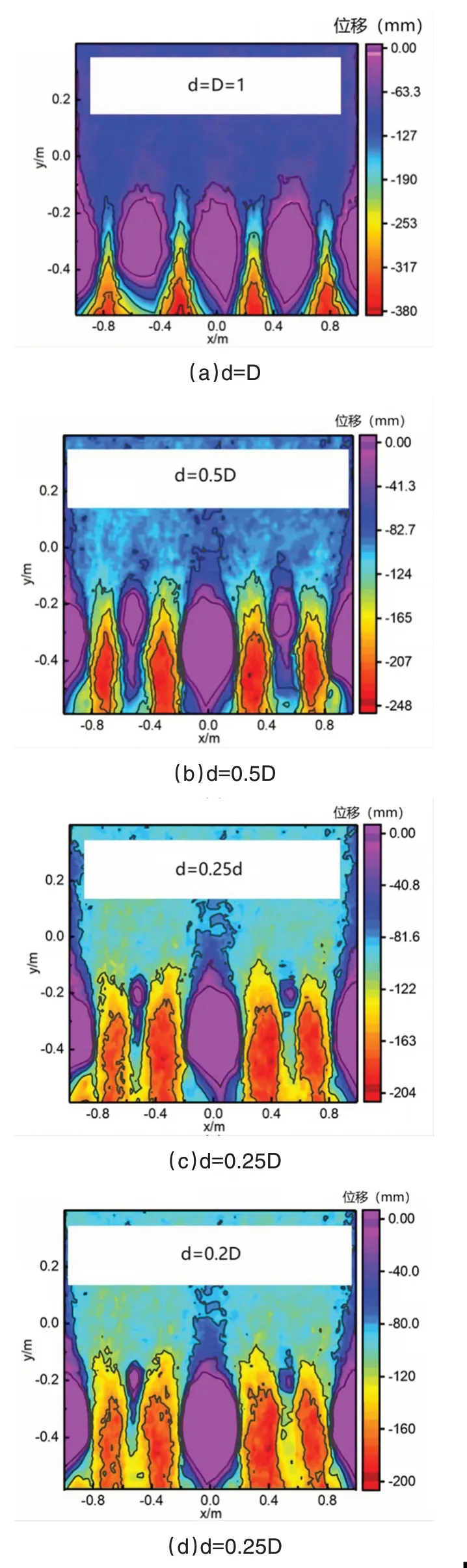
图4 土颗粒位移云图
3.2 不同摩擦系数对土拱效应的影响
为了更好地了解摩擦系数是否影响水平土拱效应,改变土壤颗粒的摩擦系数,以研究其对应力分布比和土壤颗粒位移的影响。图5 为摩擦系数为0.5、0.8 和1.0 时上部单元的应力分布比与位移的关系。上部单元最大移动100 mm。且可观察到,三条曲线的变化趋势是一致的。一旦上部单元开始移动,应力分布比迅速下降,随后趋于稳定。应力分布比随摩擦系数的增加而减小。当摩擦系数增加时,载荷传递效率将提高[8-9]。
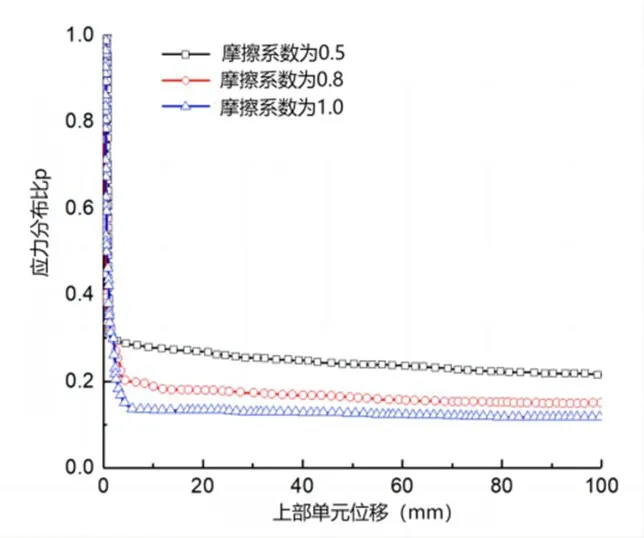
图5 不同摩擦系数下的应力分布比和上部单元位移曲线
图6 为不同摩擦系数所对应的土颗粒总位移的等值线图。从图中可以看出,随着摩擦系数的变化,土颗粒的总位移等值线并没有明显变化。进一步可说明,随着摩擦系数的增大,土拱的形状仍呈塔形,土颗粒的总位移相差不大。

图6 不同摩擦系数所对应的土颗粒总位移的等值线图
4 结论
本文采用二维离散元法对复合桩支护基坑进行了数值模拟。研究桩直径、桩位和摩擦系数对水平土拱的影响,通过本研究可以得出以下结论。
①当混凝土桩与钢管桩桩顶对齐时,应力拱为半椭圆形,相邻桩之间应力拱呈抛物线形。当钢管桩的位置向基坑内侧移动时,桩之间的应力拱为抛物线形,且应力拱逐渐减弱。
②摩擦系数逐渐增大时,对土体的位移影响不大,且对应力拱和位移拱的形状影响不大。但摩擦系数的增加会提高荷载传递效率,增强土拱的稳定性。
——结构相互作用的影响分析

