基于全息RIS的太赫兹MIMO信道估计研究

孙道远,李涛

(1.安徽工贸职业技术学院 计算机信息工程系,安徽 淮南,232001;2.九江学院 计算机与大数据科学学院,江西 九江,332005)

近年来全息通信被视为MIMO(Multiple-Input Multiple-Output)和可重构智能表面(Reconfigurable Intelligent Surfaces,RIS)辅助通信的新范式转变。目前,在全息通信研究领域,研究的重点主要集中在通信信道的建模和数据传输方面[1-3],而对于无源全息通信的物理层传输设计鲜有研究,因此文中提出了一个角域波束形成框架,通过将傅里叶分析应用于RIS单元的反射系数上,证明了具有离散单元的RIS的光束模式可以表示为Dirichlet核函数的加权积分。同时,基于提出的波束成形框架,通过推导获得了波束成形设计在两种重要情况下的封闭形式解决方案,即窄波束控制(NBS)和空间带通滤波(SBF),它们在RIS辅助通信系统中发挥着重要作用[4]。

1 系统描述和通道模型

1.1 全息通信概述

近几年,全息通信的概念逐渐被人们所关注,它作为MIMO和RIS辅助通信的新方式已经成为了一个新的研究方向[5]。全息通信的主要特征之一是将大量微小且廉价的天线或可重构元件集成到紧凑的空间中,以实现具有空间连续孔径的全息阵列。由于太赫兹电子元件的小型化,这种全息架构更容易在太赫兹频段实现。每个基于石墨烯的反射元件的尺寸为200 μm×190 μm,载波频率为0.22 THz,对应波长λ≈1 360 μm,因此反射元件的间距可以比λ/2更密集,从而形成空间连续的表面[6],这种密集或连续的RIS实现简称为全息RIS。

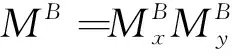
(a)当LoS路径被可能的障碍物阻挡时,BS在RIS下为多天线UE提供服务

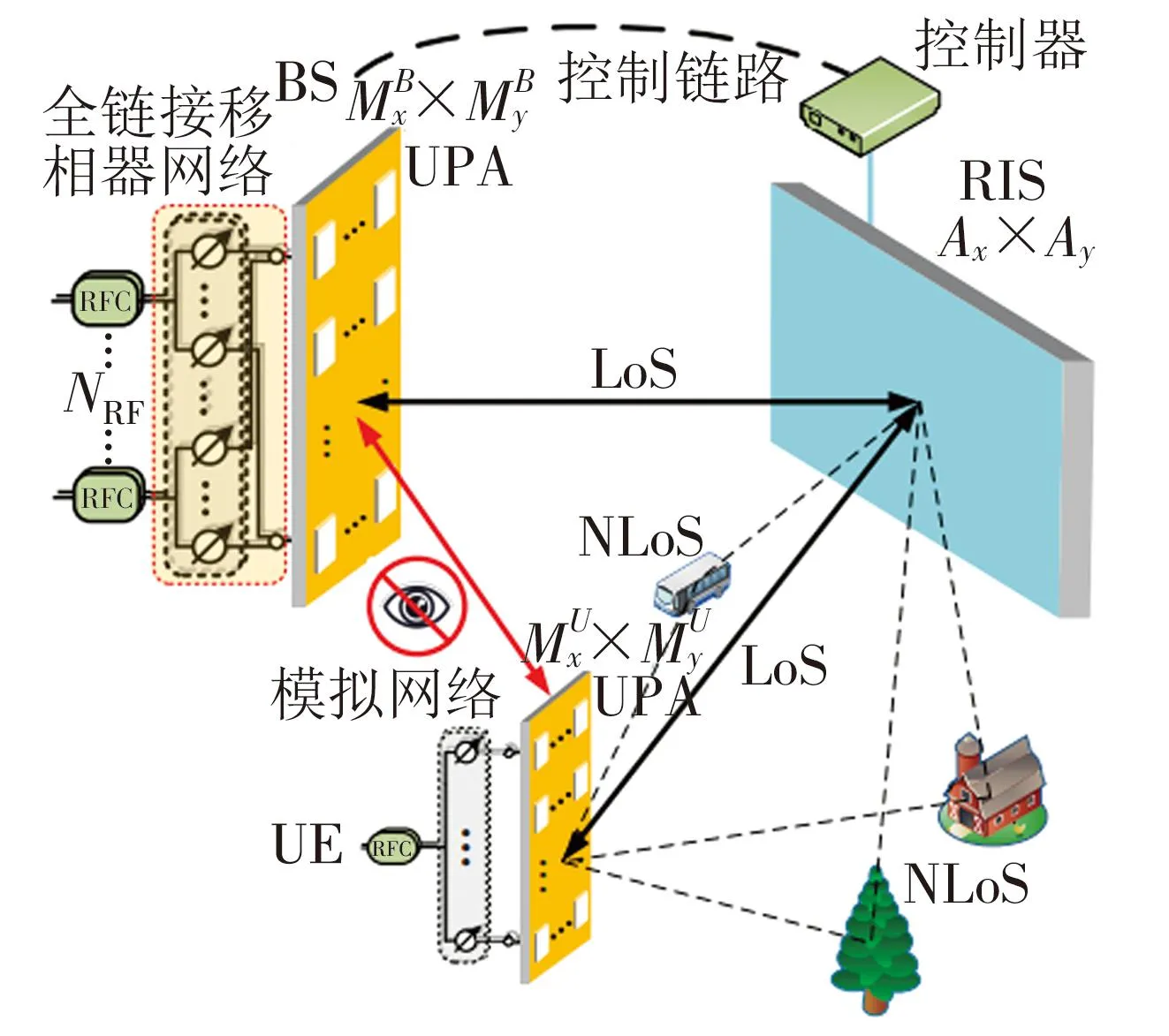
(b)BS和UE的硬件架构图1 RIS辅助太赫兹大规模MIMO系统模型

如图1(a)所示,假设BS和UE之间的LoS(时变信道)链路被障碍物或人体阻挡,那么UE仅通过RIS与BS通信,即被视为RIS辅助系统中的虚拟LoS传输[7]。为了降低功耗和硬件成本,在BS处考虑混合模数架构,即BS处只有NRFMBRFC,每个RFC通过MB相位连接到MB天线移位器。此外每个UE都采用模拟波束成形,其中只有一个RFC通过MU移相器。具有K个子载波的正交频分复用(OFDM)传输方案采用采样周期Ts。循环前缀(CP)在每个OFDM符号之前添加长度NcpTs以避免符号间干扰。中心载波频率为fc,对应波长λ[8]。

通过对RIS部署的不断调整优化,假设在BS和RIS之间存在一条LoS路径,同时BS和RIS之间的LoS角度是已知的,那么在太赫兹信道中,已知非视距(NLoS)路径的路径损耗远大于视距路径的路径损耗,所以可忽略BS和RIS之间信道中的NLoS路径。

在后文中将介绍在RIS辅助MIMO系统[9]的先前工作中广泛考虑的物理信道模型,然后通过结合BS、RIS和UE的波束成形设计,引入一个有效的基带信道模型。

1.2 离散RIS物理信道模型

假设在RIS有N个反射元素,基站到基站的下行空间信道G∈N×MB,那么RIS可以建模为

(1)

式中αDL是信道系数,aB(ψB)由式(2)给出:

(2)

对于RIS-UE空间信道H∈MU×N,设计了一个Rician衰落信道模型,它有1个LoS路径和1个NLoS路径,如图1(b)所示,具体定义为

(3)

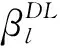
1.3 有效基带信道模型

有效基带信道定义为两个信道之间的内积收发器和转向上的模拟波束形成矢量物理信道的向量[11],表示为

(4)

式(4)中的有效基带信道模型可以推广到频率选择信道场景中,在频率选择性信道中BS-RIS-UE在延迟域中的有效基带信道可以表示为

(5)

hDL,LoS(τ)=βDL,LoSg(μLoS,ψR)gU(νLoS)p(τ-τDL,LoS),

(6)

(7)

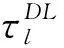
2 全息RISS的波束成形设计

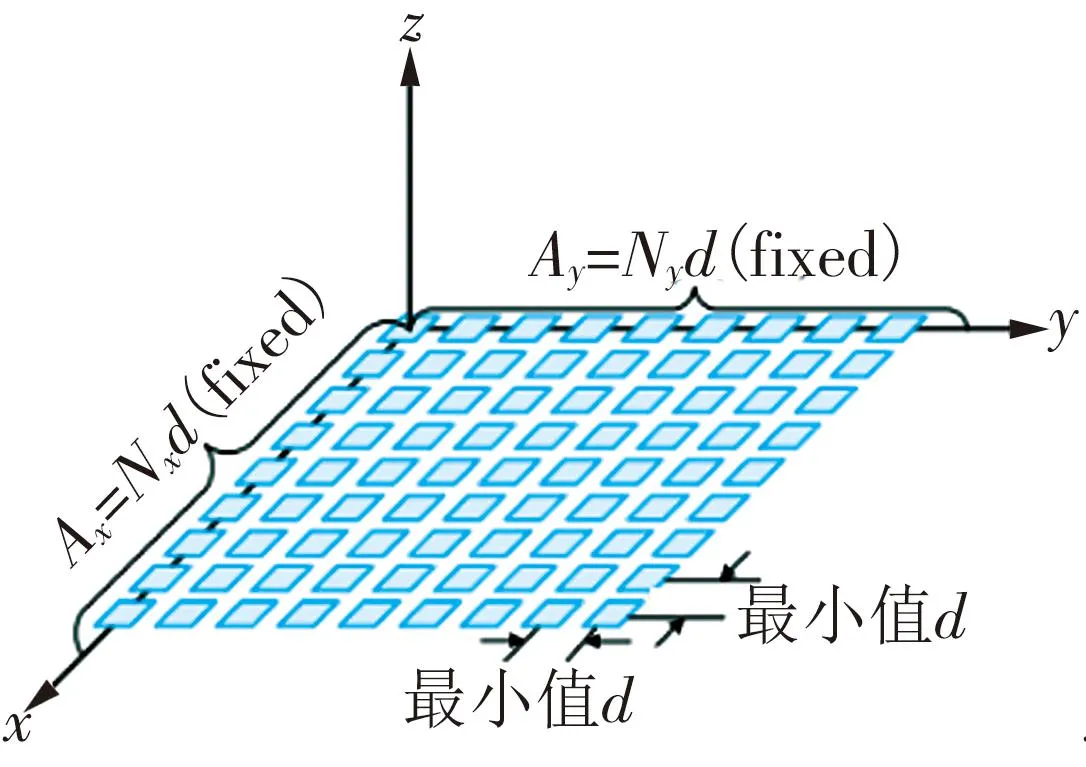
完成有效基带式(5)～(7)中的信道模型,首先推导和分析基于离散平面阵列(DPA)的RIS的光束模式,然后将结果扩展到空间连续的RIS孔径并称其为连续超表面(CMS)。

2.1 基于离散平面阵列的RIS

将基于DPA的RIS放置在x-y平面,其由许多均匀分布的反射元素组成,具体由如图2(a)和图2(b)所示。

(a)d=0.5λ的临界间隔RIS

(b)d<0.5λ的超密集RIS,具有空间准连续孔径

(c)d→0的CMS(忽略单个反射元件的物理尺寸),具有理想的可重构连续孔径图2 不同类型RIS的图示

沿x和y方向的元素数分别为Nx∈和Ny∈。两个相邻元素之间的距离为d,基于奈奎斯特采样定理假设d≤λ=2,定义基于DPA的RIS的大小为Ax×Ay,其中Ax=Nxd,Ay=Nyd,并假设Ax和Ay保持不变。接收信号沿方向入射信号后的观察(即反射)用g(ψout,ψin)表示,即由所有反射的信号的叠加给出RIS的个别元素:

(8)

通过前述定义称g(ψout,ψin)为基于DPA的RIS的波束方向图,与式(4)中的定义一致。g(ψout,ψin)的幅度可用于评估来自RIS反射后沿向外方向的信号强度。Φ(m,n)为空间域中的二维离散信号,通过使用离散时间傅里叶变换(DTFT)得到式(9):

(9)

式(9)揭示了光束模式(ψout,ψin)同时可表述为Dirichlet核函数Ξ(·)的加权积分,其权重因子为ω′(k,l)。

2.2 基于DPA的RIS波束成形设计

就基于DPA的RIS的设计而言,已考虑元素间距d=λ=2,其原理是基于奈奎斯特采样定理的临界间距,但是基于临界距离间隔的元素的RIS设计和优化具有一些固有的缺点,特别是:

1)由于周期性和不可忽略的狄利克雷核函数,功率泄漏是非常普遍的现象,这可能导致光束间的干扰;

2)对于接收和反射的能量RIS高度依赖于其有效反射面积。更具体地说,使用临界间隔的RIS通常会降低有效反射面积,这可能导致能源效率降低。

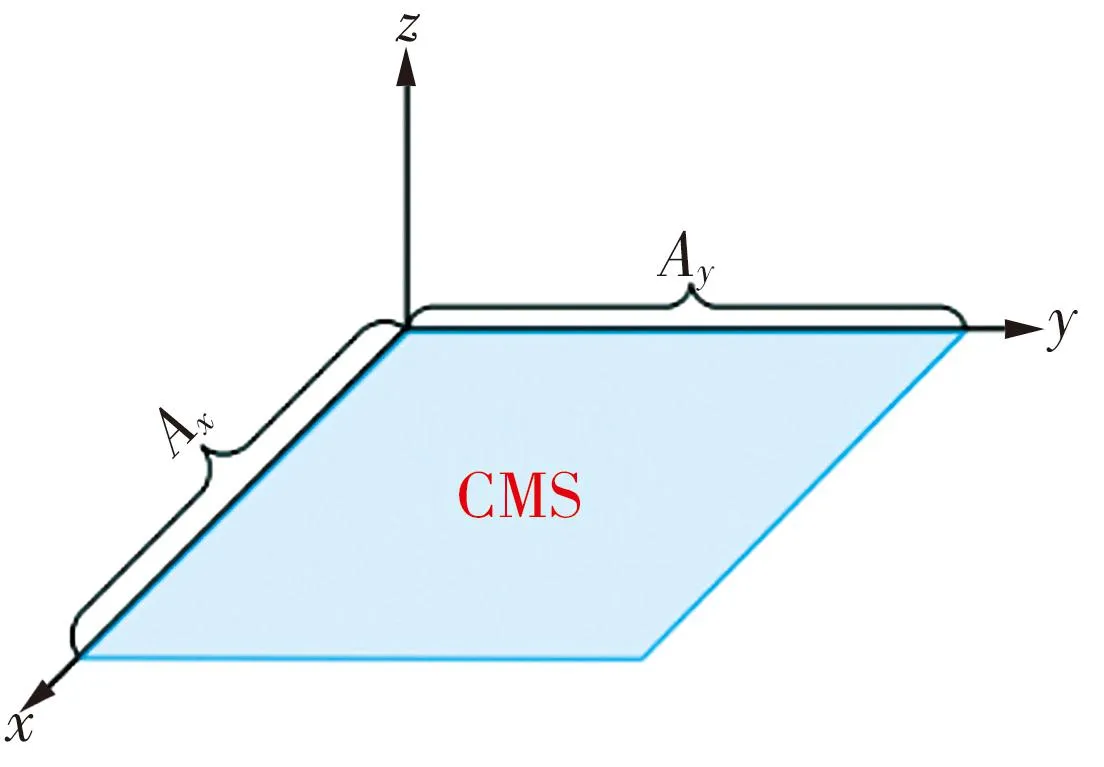
由于RIS的物理尺寸受若干实际因素的限制,对于前述提到的缺点,其有效解决方案是增加反射次数元素并减少它们的间距(d<λ/2),同时保持Ax和Ay不变,如图2(b)所示,基于DPA的RIS其元素间距d<λ/2,因此也被称为超密集RIS。应通过应用临界间隔和超密集RIS适当地选择d值,图3～4展示了基于DPA的RIS的光束模式d的不同值,可以观察到光束模式下d={λ/4,λ/8}的超密集RIS。与临界间隔的RIS相比,通过增加反射元件的数量,超密集RIS的有效反射面积预计将增加,因此入射EM信号的能量的更大部分可以被引导到期望的方向。

图3 归一化幅度的NBS波束方向图

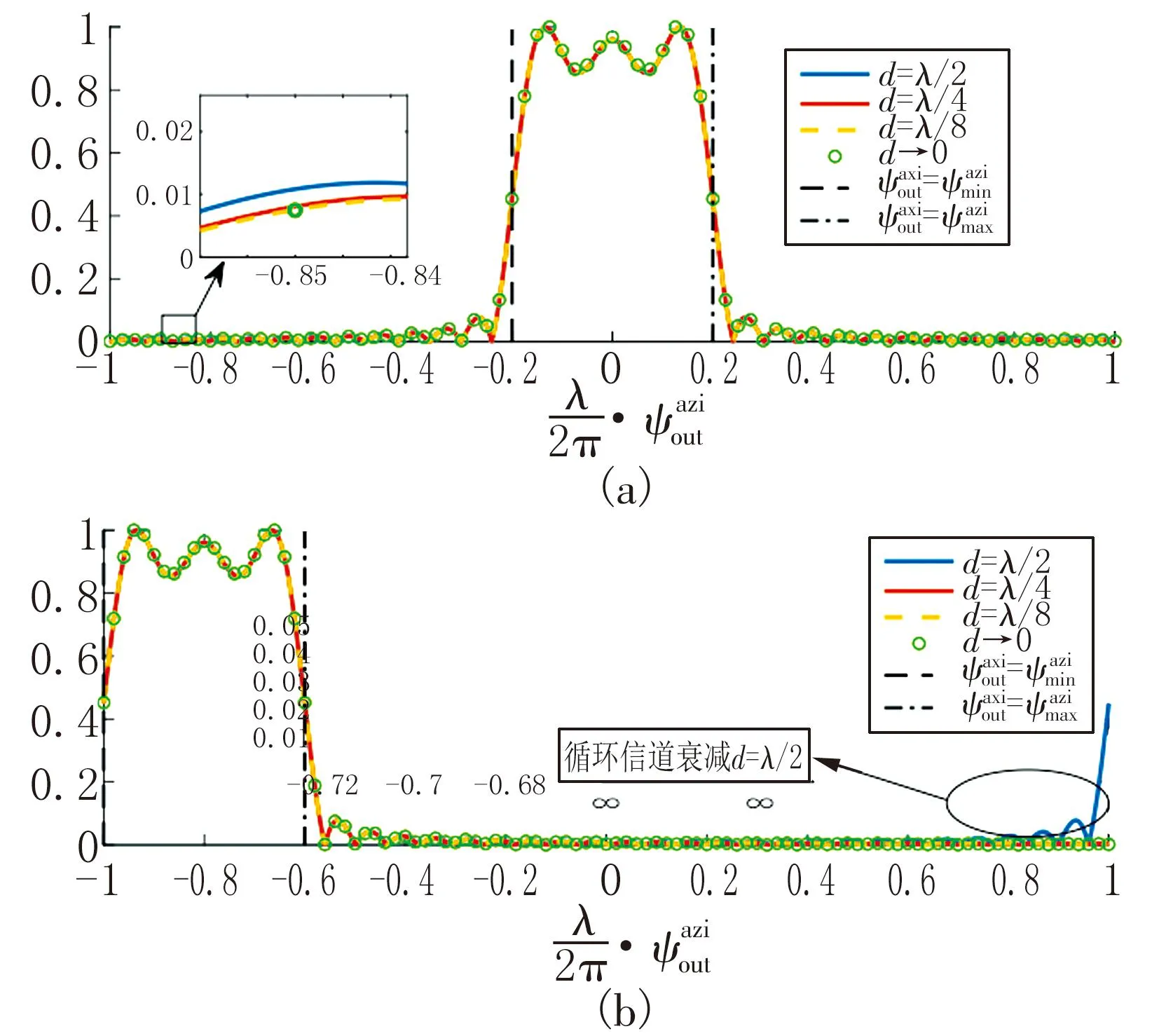
图4 归一化幅度的SBF波束方向图

(10)

(11)

3 闭环信道估计方案

3.1 传输结构设计

在前述内容的基础上,将进一步研究全息RIS应用于太赫兹大规模MIMO系统的CE问题,所设计的传输帧结构如图5所示。TDL、TUL分别为下行、上行CE阶段的导频开销,Tcoh为信道相干时间。

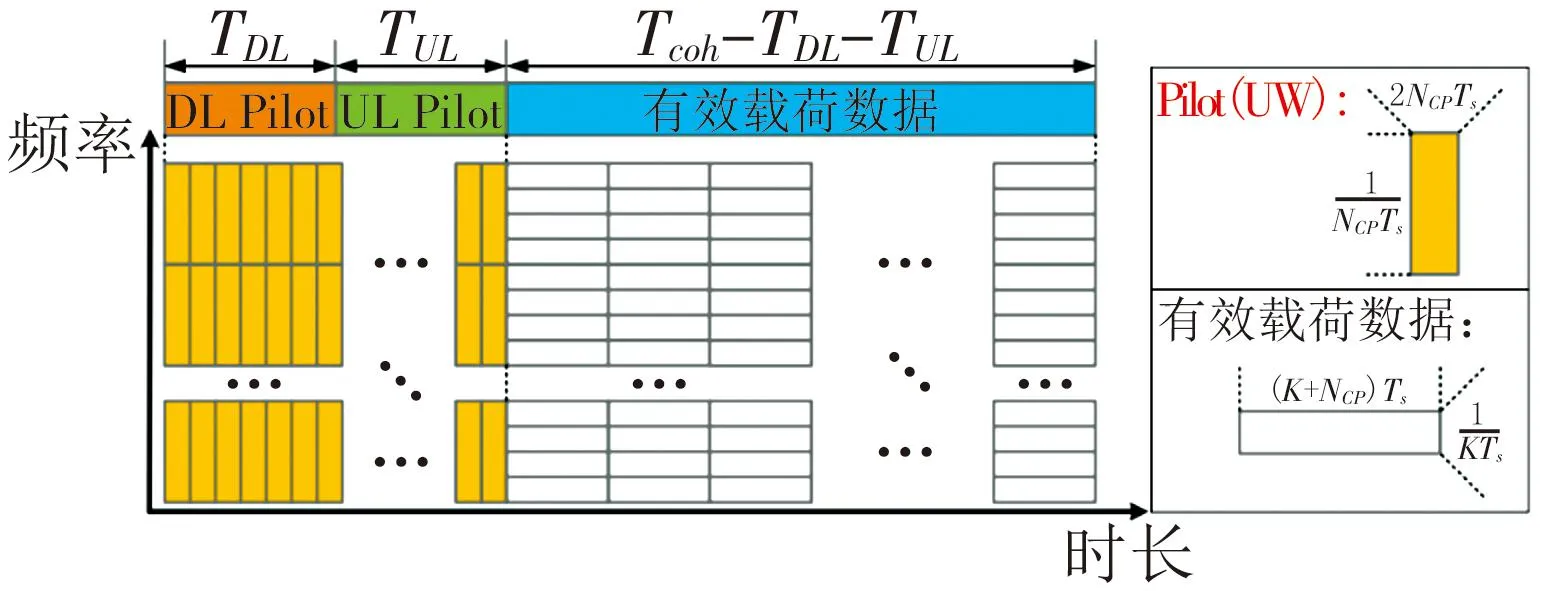
图5 系统传输帧结构

在整个CE阶段,短长度的OFDM符号即唯一词(UW)将被作为导频信号发送。每个UW都由NCP频域中的子载波组成,其长度(持续时间)=2NCPTs,如图6所示。对于每个在BS上的RFC,假设波束成形为NBS获得高波束赋形增益、BS-RIS信道的LoS方向为已知,那么在BS每个RFC的波束成形可设计为

图6 总导频开销和计算量之间的权衡

(12)

关注恒模的约束混合满足模数架构隐式的同时也考虑了NBS波束成形。所有的信号将RFC添加到一起并获得单个数据流。因此,可通过删除式(5)中的索引将其重写为

hDL(τ)=αDLGB[hDL,LoS(τ)+hDL,NLoS(τ)],

(13)

文中所提出的CS(Compressive Sensing压缩传感)方案包括两个阶段,分别被应用于下行链路传输和上行链路传输。

3.2 计算复杂性分析

1)下行链路计算复杂度

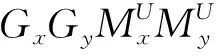
2)上行链路计算复杂度

上行链路的复杂度主要是由上行CE算法决定的。由于CE问题已被表述为稀疏信号恢复,针对上行CE采用的OMP算法而言,考虑复值乘法的总数评估计算复杂度。

4 试验分析

4.1 试验设置

文中设计系统模型如图7所示。

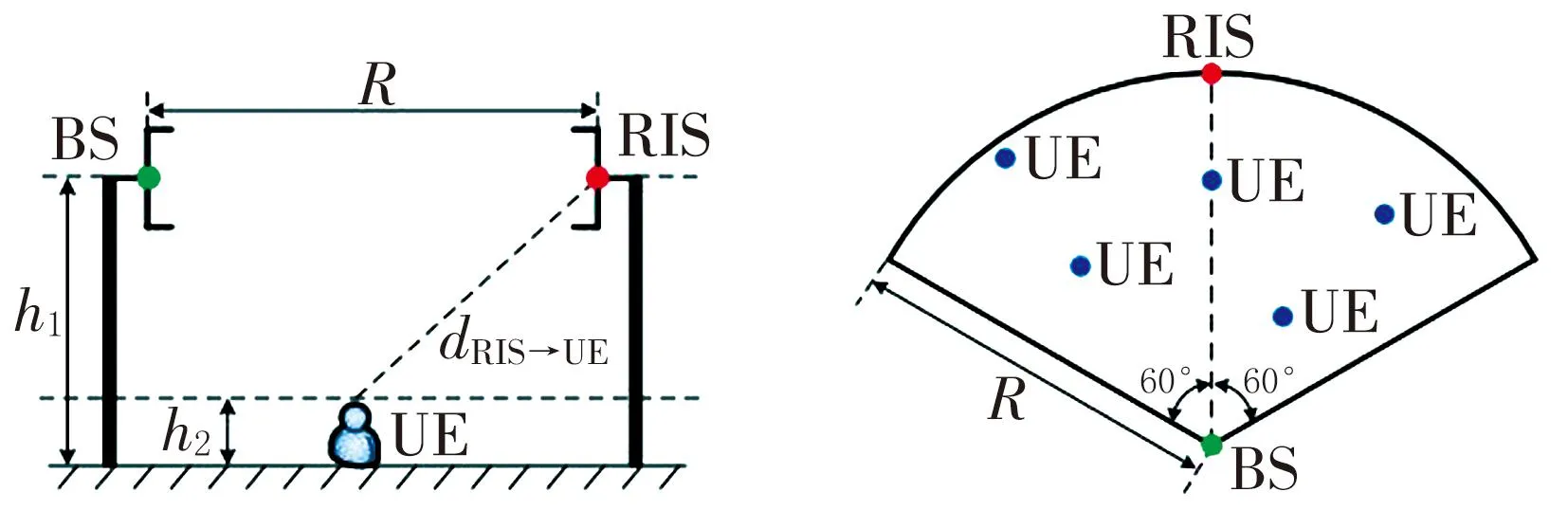
(a)侧视图 (b)顶视图图7 RIS辅助的太赫兹大规模MIMO系统

BS/RIS分布在一个扇区内,其为UE提供服务的区域半径为R、中心角为120°。BS和RIS的高度为h1,UE的高度为h2,假设数组的法线方向在BS和RIS相互指向上产生ψB=ψR=[0,0]T。

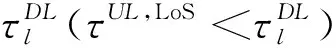
(14)

(15)

式中:θα、θβ～U[0,2π)为引入的相移通道;Seff为RIS的有效反射面积;dRIS→UE为UE和RIS之间的距离;GTx、GRIS和GRx为包含了BS、RIS和UE的数组;Aabs(fc,dTx→Rx)与载波频率fc和传输距离dTx→Rx有关,其具体值是根据国际电信联盟的建议得到的。RIS的有效反射面积Seff可以建模为其整个物理区域(孔径):

(16)

式中Sele≤d2为基于DPA的RIS中的元素单次反射的物理尺寸,假设Sele≈200 μm×200 μm。上行信道的参数可以类似地建模。

4.2 结果分析

图7显示了当NP=40时所需的导频开销和计算复杂度与组数{Gx,Gy}的关系。可以看到通过设置不同的组{Gx,Gy},所提出的闭环方案能够提供一个导频开销和计算复杂度之间的合理权衡。图7中有两种情况值得进一步关注:

1)Gx=Gy=1的情况,指上行链路中的完整信道(以开环方式)。在这种情况下,估计上行信道矩阵的总大小为40 000×64,这会使计算复杂度和存储负担过高。

2)Gx=2Ax/λ=200和Gy=2Ay/λ=200的情况,指仅在下行链路中通过穷举波束扫描获取完整的CSI。这种情况会因长TDL(如图7所示大约0.6s)的影响而降低净频谱效率。

图8显示了下行链路CE阶段的准确性。将其得到的指标与oracleμLoS和νLoS角度进行比较,判断下行CE是否成功。其中考虑了3种不同类型的RIS,即临界间隔RIS(d=λ/2)、超密集RIS(d<λ/2)和CMS(d→0),可以观察到文中提出的CMS在3种类型的RIS中提供了最好的性能。

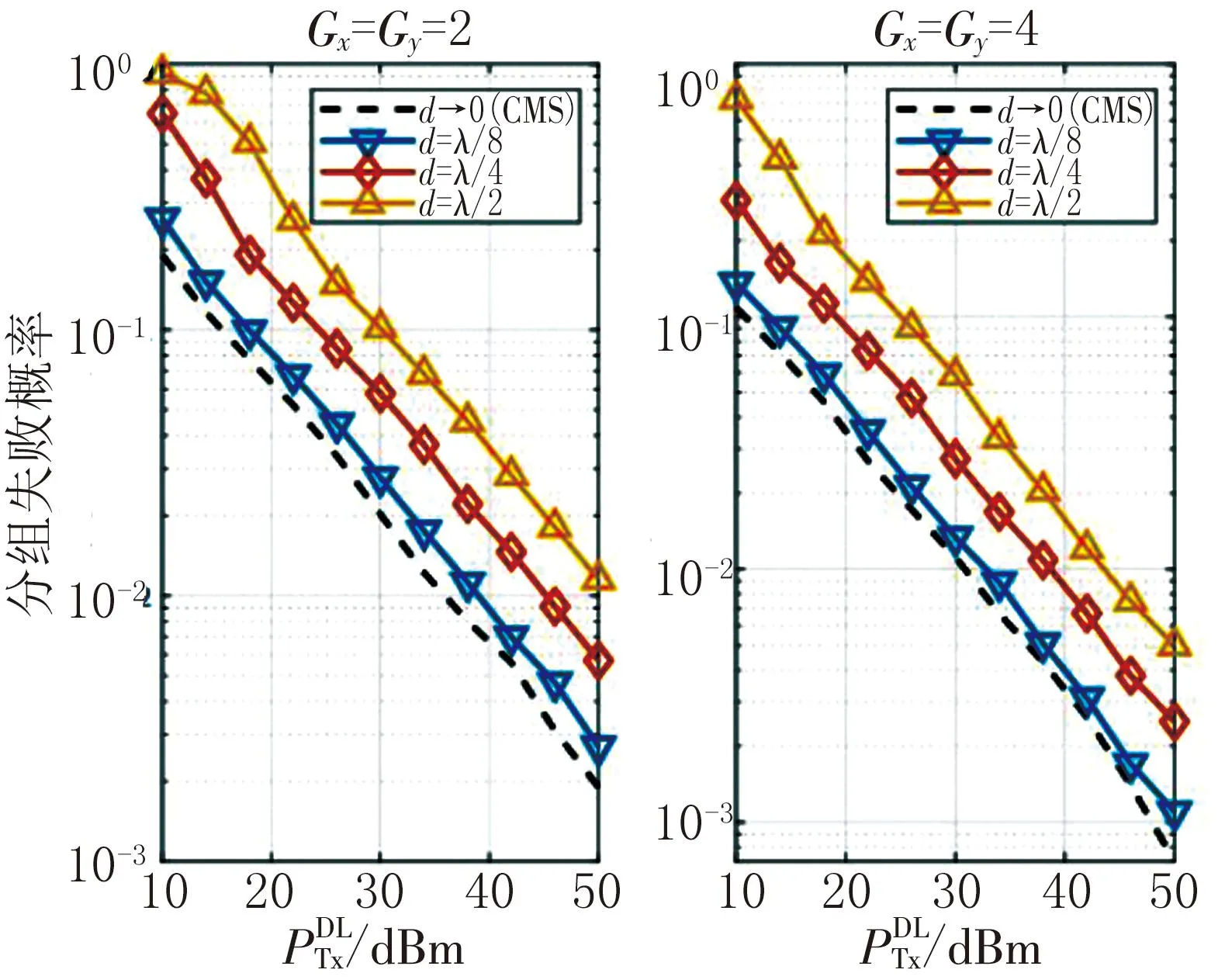
图8 下行链路CE性能与BS发射功率的关系

超密集RIS的性能明显优于传统的临界间隔RIS,因为超密集RIS具有更大的有效反射面积和更小的旁瓣(主瓣中更高的阵列增益),从而带来更好的接收信噪比(信噪比)。

设置Gx=Gy=10,即Bx=By=20,在图9～11中,将归一化均值采用平方误差(NMSE)作为性能指标感。图9描绘了上行链路NMSE性能与上行链路导频开销NP和不同的DSC分配方案。

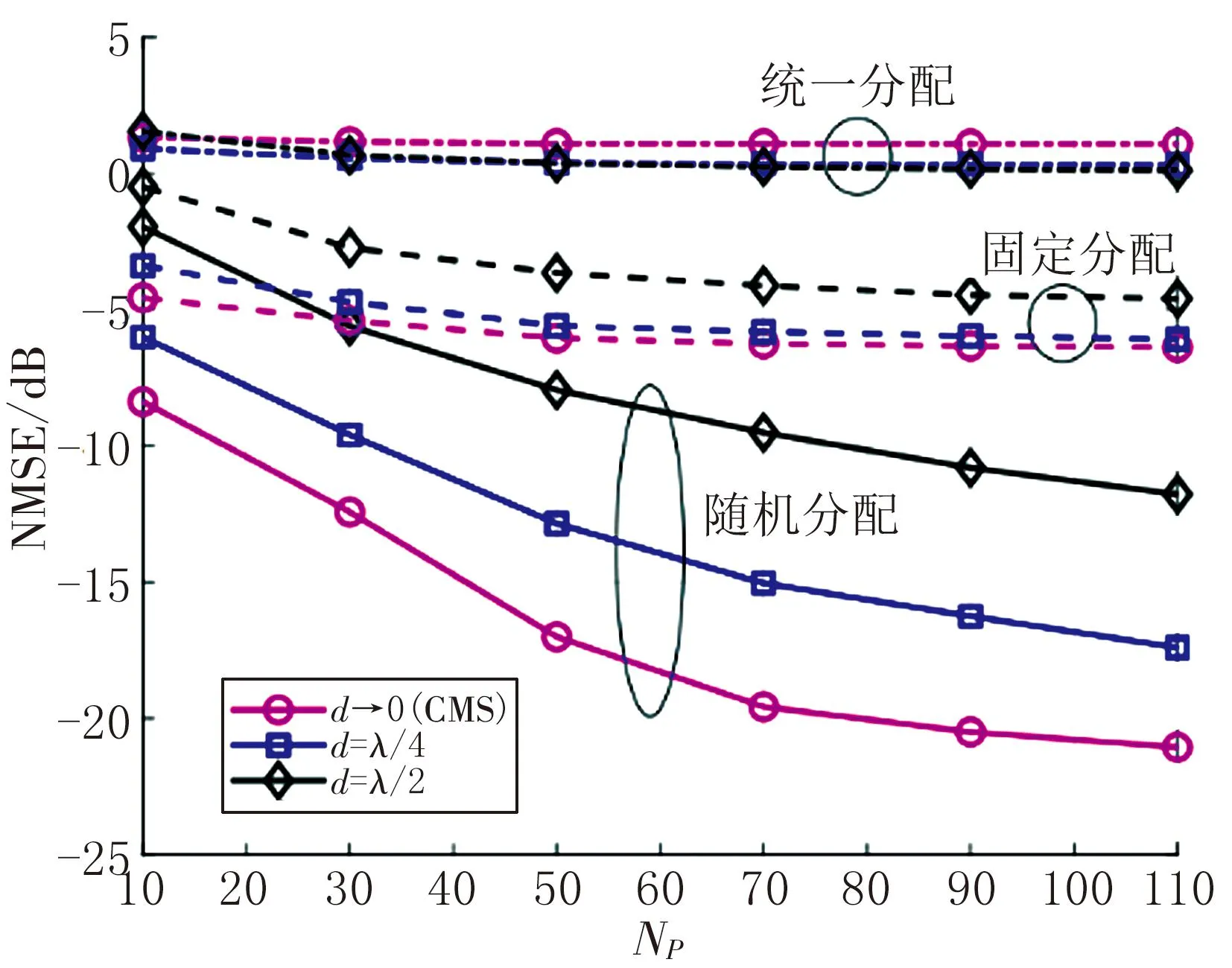
图9 NMSE性能与上行链路导频开销

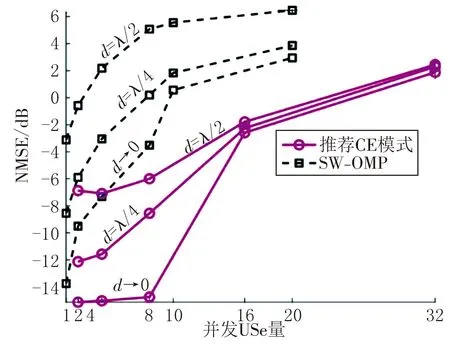
图10 NMSE性能验证

图11 不同CE方案的NMSE性能对上行传输功率的影响

由图9可以观察到,随机DSC分配方案实现了更好的CE性能,同时可以确保即使压缩比(NPNused)/(BxByNCP)低但只要在{0.006 3,0.018 7,0.031 3,0.043 7,0.056 3,0.068 8}范围内,就能够有足够高的CE精度。图10绘制了所提出算法的NMSE性能。图11比较了NMSE性能不同的CE方案对上行发射功率的影响。

5 结论

在全息通信研究的大背景下,本文研究了太赫兹波段全息RIS的物理层传输,其中大量亚波长可重构元件密集集成到紧凑空间中以接近空间连续孔径。推导出了全息RIS的光束模式,提出了两种以封闭形式表达的波束成形设计,并基于此设计,提出了一种用于RIS辅助太赫兹大规模MIMO系统的闭环宽带CE方案。同时为了减少导频开销,提出了一种基于CS(压缩感知)的CE算法,该算法利用了对偶太赫兹MIMO信道在角域和延迟域中的稀疏性。仿真结果表明,全息RIS优于传统的非全息RIS设计且不使用RIS的通信方案。