筋土峰值拉拔力的影响因素研究
姚文杰,李明宝,郑俊杰,郭亿辉



摘要:为解决加筋土结构中筋土界面间复杂效应问题,采用筋材的微单元受力平衡方法,考虑剪切刚度与位移的影响,推导筋土峰值拉拔力计算公式;预测筋材在所受拉力不超过其峰值拉拔力的情况下各个位置的拉力及位移;在最大峰值拉拔力的范围内分析筋材有效加筋长度、剪切刚度对筋材位移的影响及其变化规律。结果表明,在峰值拉拔力一定的情况下,筋材的有效加筋长度与剪切刚度对峰值拉拔力的影响较为显著,而弹性模量对峰值拉拔力的影响较小,筋材位移随着筋材有效加筋长度、剪切刚度的增大而呈非线性减小。将采用筋土界面峰值拉拔力公式的计算结果与拉拔试验的试验结果进行对比分析,发现两者的最大峰值拉拔力相差不大,结果吻合较好。研究成果可以为加筋土工程提供一定的理论参考。
关键词:筋土界面;峰值拉拔力;剪切刚度;有效加筋长度;弹性模量
中图分类号:U416.1文献标识码:A文章编号:1006-8023(2024)01-0201-06
Study on the Factors Influencing the Peak Tensile Force of Reinforced Soil
YAO Wenjie1, LI Mingbao1*, ZHENG Junjie2, GUO Yihui1
(1.School of Civil Engineering and Transportation, Northeast Forestry University, Harbin 150040, China; 2.School of Civil and Hydraulic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)
Abstract:In order to solve the problem of complex effects between the reinforced soil interface in reinforced soil structures, the paper adopted the micro-unit force balance method of the reinforcing material, considered the effects of shear stiffness and displacement, and derived the formula for the peak tensile force of reinforced soil. The tensile forces and displacements of the reinforcement at each location were predicted if the tensile forces do not exceed the peak pullout force. The maximum peak tensile force was determined, and the effect of effective reinforcement length and shear stiffness on the displacement of reinforcement and its variation rule were investigated within the range of maximum peak tensile force. The results showed that when the peak tensile force was constant, the effective reinforcement length and shear stiffness had a significant effect on the peak tensile force, while the elastic modulus had a relatively small effect on the peak tensile force. The displacement of the reinforcement decreased nonlinearly with the increase of the effective reinforcement length and shear stiffness. The calculation results based on the formula of peak tensile force at the interface of reinforced soil were compared with the test results. It was found that the maximum peak tensile force between the two was not different, and the results agreed well. The research results can provide some theoretical reference for reinforced soil engineering.
Keywords:Reinforced soil interface; peak drawing force; shear stiffness; effective reinforcement length; modulus of elasticity
0引言
隨着加筋土技术的快速发展,土工格栅在加筋地基、加筋挡土墙中的应用已越来越广泛。而筋土界面的相互作用直接影响加筋体的稳定性,同时由于筋材与其周围土体相互作用参数的多样性,筋土界面复杂的特性也严重影响了加筋土技术的发展[1]。
筋土界面相互作用的特性十分复杂,不仅与土体的颗粒级配、相对密度、抗剪强度和上覆土压力等有关[2],而且受土工格栅的几何形状、受力方向、有效加筋长度和剪切刚度等的影响[3-4]。这些因素导致筋土界面的研究有许多的不确定因素,因此对筋土界面特性进行研究是非常必要的。
现有很多学者对筋土界面的受力状况进行理论分析。GURUNG等[5]采用双曲线模型对筋土界面的剪应力与位移的关系进行分析。赖丰文等[6]利用弹性-指数软化模型以及参数分析的方法对剪应力与位移之间的关系进行研究。杜常博等[7]通过双线性模型及三线性模型对筋土拉拔界面的弹塑性变形的全过程进行分析。
以上学者通过理论分析的方法完善了筋土界面的相关问题研究。然而大部分学者通过剪切试验以及拉拔试验对筋土界面的受力状况进行分析。Wang等[8]采用单调直剪(MDS)试验、循环直剪(CDS)试验和后循环直剪(PCDS)试验,发现界面黏聚力和摩擦角均随粗粒土粒径的增大而增大。王军等[9]采用大型动态直剪仪对相对密实度75%的砾石和土工格栅的界面进行研究,从而提出了界面剪切应力-剪切位移表达式。Basudhar [10]基于莫尔-库伦准则对模型参数的研究对2种不同质地的土工织物的峰值界面剪切强度进行对比。康博文等[11]采用拉拔试验对不同P5(粒径>5 mm的粗颗粒质量百分比)含量的砂砾土进行试验,系统地研究了该含量下的砂砾土对峰值拉拔力的影响。刘飞禹等[12]通过循环剪切试验分析了循环次数与剪切刚度之间的关系。丁金华等[13]通过室内拉拔试验,探究了法向应力、砂垫层厚度和土工格栅横肋间距对加筋体极限拉拔力的影响。
此外,部分学者通过数值模拟的方法去描述筋土界面的相互作用关系。Wang等[14]基于离散元分析方法对荷载作用下的筋土界面的力学响应进行研究,得出土工格栅平面内法向应力的分布规律。王志杰等[15]基于离散元数值模拟,对刚性与柔性顶部边界条件下的筋土界面力学特性进行了深入的研究。Miao等[16]基于离散元数值模拟的方法,分析了颗粒形状对拉拔试验结果的影响。
本研究基于筋土界面的拉拔力与剪应力的相互作用关系,得到峰值拉拔力的表达式。由此确定最大峰值拉拔力(F0 m)。并且在峰值拉拔力F0≤F0 m的限制范围内,讨论有效加筋长度(l)、加筋体剪切刚度(G)和界面摩擦效应(f)等因素对峰值拉拔力的影响。
1峰值拉拔力本构关系
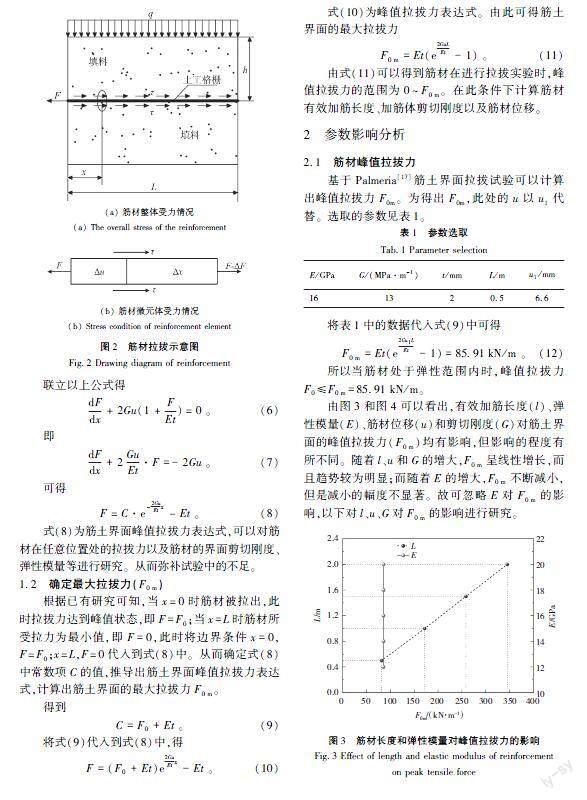
本研究以桩承式加筋路堤为背景,研究桩上筋土界面的力学特性。建立筋土界面模型,如图1所示。由于荷载的传递作用,土层荷载传递至路基,而后又将传递至桩帽。由于桩帽、土体支撑和土工合成材料与桩体之间的作用十分复杂。故先对土工格栅与土体间的效应进行研究。
1.1筋土界面峰值拉拔力推导
为研究土工格栅与土体间的作用关系,建立图2(a)的筋材整体受力情况示意图[6],在试验中将槽底和侧向边界固定,并且在顶端的承压板上施加竖直向下的均布荷载。筋材的长度为L,厚度为t,弹性模量为E。
图2(b)为筋材微单元体受力情况示意图,长度为Δx,宽度取单位宽度。由受力平衡可得
F-(F-ΔF)-2τ(Δx+Δu)=0。(1)
式中:F为筋材左端受到的拉力;F-ΔF为筋材右端受到的拉力;ΔF为拉拔过程中自由端与拉拔端受力的差值;τ为界面剪切应力;Δu为微单元体Δx的变形。
在x处筋材的应变(ε)
ε=ΔuΔx。 (2)
由此可得
dFdx-2τ(1+ε)=0 。 (3)
應变与单位宽度的拉拔力关系可表示为
ε=FEt。 (4)
式中:E为筋材的弹性模量;t为筋材厚度。
在未达到峰值拉拔力时,筋材处于弹性范围内
τ=Gu。(5)
此时,界面剪切应力(τ)与加筋体剪切刚度(G)、筋材拉拔位移(u)有关。
联立以上公式得
dFdx+2Gu(1+FEt)=0 。 (6)
即
dFdx+2GuEt·F=-2Gu。(7)
可得
F=C·e-2GuEtx-Et。(8)
式(8)为筋土界面峰值拉拔力表达式,可以对筋材在任意位置处的拉拔力以及筋材的界面剪切刚度、弹性模量等进行研究。从而弥补试验中的不足。
1.2确定最大拉拔力(F0 m)
根据已有研究可知,当x=0时筋材被拉出,此时拉拔力达到峰值状态,即F=F0;当x=L时筋材所受拉力为最小值,即F=0,此时将边界条件x=0,F=F0;x=L,F=0代入到式(8)中。从而确定式(8)中常数项C的值,推导出筋土界面峰值拉拔力表达式,计算出筋土界面的最大拉拔力F0 m。
得到
C=F0+Et。 (9)
将式(9)代入到式(8)中,得
F=(F0+Et)e2GuEtx-Et。(10)
式(10)为峰值拉拔力表达式。由此可得筋土界面的最大拉拔力
F0 m=Et(e2GuLEt-1)。(11)
由式(11)可以得到筋材在进行拉拔实验时,峰值拉拔力的范围为0~F0 m。在此条件下计算筋材有效加筋长度、加筋体剪切刚度以及筋材位移。
2参数影响分析
2.1筋材峰值拉拔力
基于Palmeria[17]筋土界面拉拔试验可以计算出峰值拉拔力F0m。为得出F0m,此处的u以u1代替。选取的参数见表1。
将表1中的数据代入式(9)中可得
F0 m=Et(e2Gu1LEt-1)=85.91 kN/m 。(12)
所以当筋材处于弹性范围内时,峰值拉拔力F0≤F0 m=85.91 kN/m。
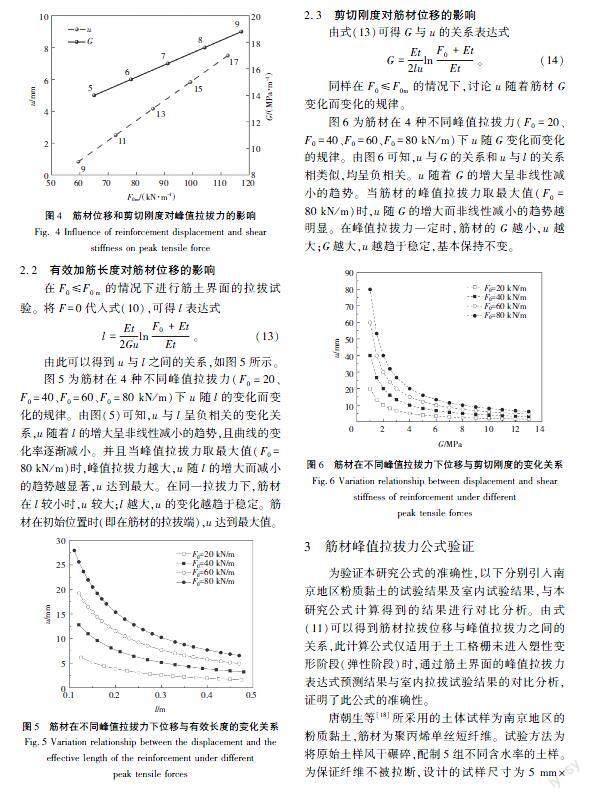
由图3和图4可以看出,有效加筋长度(l)、弹性模量(E)、筋材位移(u)和剪切刚度(G)对筋土界面的峰值拉拔力(F0 m)均有影响,但影响的程度有所不同。随着l、u和G的增大,F0 m呈线性增长,而且趋势较为明显;而随着E的增大,F0 m不断减小,但是减小的幅度不显著。故可忽略E对F0 m的影响,以下对l、u、G对F0 m的影响进行研究。
2.2有效加筋长度对筋材位移的影响
在F0≤F0 m的情况下进行筋土界面的拉拔试验。将F=0代入式(10),可得l表达式
l=Et2GulnF0+EtEt。(13)
由此可以得到u与l之间的关系,如图5所示。
图5为筋材在4种不同峰值拉拔力(F0=20、F0=40、F0=60、F0=80 kN/m)下u随l的变化而变化的规律。由图(5)可知,u与l呈负相关的变化关系,u随着l的增大呈非线性减小的趋势,且曲线的变化率逐渐减小。并且当峰值拉拔力取最大值(F0=80 kN/m)时,峰值拉拔力越大,u随l的增大而减小的趋势越显著,u达到最大。在同一拉拔力下,筋材在l较小时,u较大;l越大,u的变化越趋于稳定。筋材在初始位置时(即在筋材的拉拔端),u达到最大值。
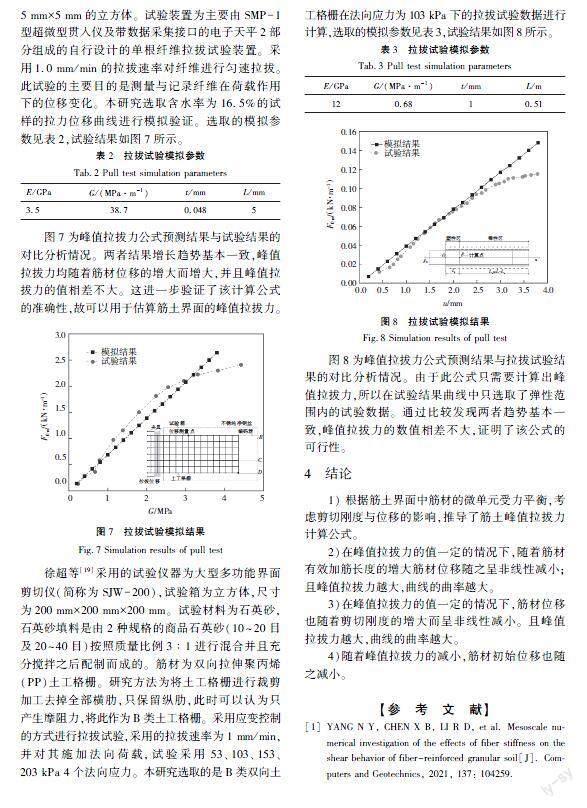
2.3剪切刚度对筋材位移的影响
由式(13)可得G与u的关系表达式
G=Et2lulnF0+EtEt。(14)
同样在F0≤F0m的情况下,讨论u随着筋材G变化而变化的规律。
图6为筋材在4种不同峰值拉拔力(F0=20、F0=40、F0=60、F0=80 kN/m)下u随G变化而变化的规律。由图6可知,u与G的关系和u与l的关系相类似,均呈负相关。u随着G的增大呈非线性减小的趋势。当筋材的峰值拉拔力取最大值(F0=80 kN/m)时,u随G的增大而非线性减小的趋势越明显。在峰值拉拔力一定时,筋材的G越小,u越大;G越大,u越趋于稳定,基本保持不变。
3筋材峰值拉拔力公式验证
为验证本研究公式的准确性,以下分别引入南京地区粉质黏土的试验结果及室内试验结果,与本研究公式计算得到的结果进行对比分析。由式(11)可以得到筋材拉拔位移与峰值拉拔力之间的关系,此计算公式仅适用于土工格栅未进入塑性变形阶段(弹性阶段)时,通过筋土界面的峰值拉拔力表达式预测结果与室内拉拔试驗结果的对比分析,证明了此公式的准确性。
唐朝生等[18]所采用的土体试样为南京地区的粉质黏土,筋材为聚丙烯单丝短纤维。试验方法为将原始土样风干碾碎,配制5组不同含水率的土样。为保证纤维不被拉断,设计的试样尺寸为5 mm×5 mm×5 mm的立方体。试验装置为主要由SMP-1型超微型贯入仪及带数据采集接口的电子天平2部分组成的自行设计的单根纤维拉拔试验装置。采用1.0 mm/min的拉拔速率对纤维进行匀速拉拔。此试验的主要目的是测量与记录纤维在荷载作用下的位移变化。本研究选取含水率为16.5%的试样的拉力位移曲线进行模拟验证。选取的模拟参数见表2,试验结果如图7所示。
图7为峰值拉拔力公式预测结果与试验结果的对比分析情况。两者结果增长趋势基本一致,峰值拉拔力均随着筋材位移的增大而增大,并且峰值拉拔力的值相差不大。这进一步验证了该计算公式的准确性,故可以用于估算筋土界面的峰值拉拔力。
徐超等[19]采用的试验仪器为大型多功能界面剪切仪(简称为SJW-200),试验箱为立方体,尺寸为200 mm×200 mm×200 mm。试验材料为石英砂,石英砂填料是由2种规格的商品石英砂(10~20目及20~40目)按照质量比例3∶1进行混合并且充分搅拌之后配制而成的。筋材为双向拉伸聚丙烯(PP)土工格栅。研究方法为将土工格栅进行裁剪加工去掉全部横肋,只保留纵肋,此时可以认为只产生摩阻力,将此作为B类土工格栅。采用应变控制的方式进行拉拔试验,采用的拉拔速率为1 mm/min,并对其施加法向荷载,试验采用53、103、153、203 kPa 4个法向应力。本研究选取的是B类双向土工格栅在法向应力为103 kPa下的拉拔试验数据进行计算,选取的模拟参数见表3,试验结果如图8所示。
图8为峰值拉拔力公式预测结果与拉拔试验结果的对比分析情况。由于此公式只需要计算出峰值拉拔力,所以在试验结果曲线中只选取了弹性范围内的试验数据。通过比较发现两者趋势基本一致,峰值拉拔力的数值相差不大,证明了该公式的可行性。
4结论
1) 根据筋土界面中筋材的微单元受力平衡,考虑剪切刚度与位移的影响,推导了筋土峰值拉拔力计算公式。
2)在峰值拉拔力的值一定的情况下,随着筋材有效加筋长度的增大筋材位移随之呈非线性减小;且峰值拉拔力越大,曲线的曲率越大。
3)在峰值拉拔力的值一定的情况下,筋材位移也随着剪切刚度的增大而呈非线性减小。且峰值拉拔力越大,曲线的曲率越大。
4)随着峰值拉拔力的减小,筋材初始位移也随之减小。
【参考文献】
[1]YANG N Y, CHEN X B, LI R D, et al. Mesoscale numerical investigation of the effects of fiber stiffness on the shear behavior of fiber-reinforced granular soil[J]. Computers and Geotechnics, 2021, 137: 104259.
[2]王军,林旭,符洪涛.砂土-格栅筋土界面特性的本构模型研究[J].岩土力学,2014,35(S2):75-84.
WANG J, LIN X, FU H T. Study of constitutive model of sand-geogrid interface behavior in geogrid/geotextile reinforced soil[J]. Rock and Soil Mechanics, 2014, 35(S2): 75-84.
[3]李磊.不同土工合成材料与再生混凝土骨料的界面剪切特性研究[D].赣州:江西理工大学,2021.
LI L. Research on shear characteristics of interfaces between different geosynthetics and recycled concrete aggregate[D]. Ganzhou: Jiangxi University of Science and Technology, 2021.
[4]万小龙,刘运思,郭志广,等.加筋路基边坡筋土界面应变软化模型研究[J].公路工程,2023,48(2):68-72,103.
WAN X L, LIU Y S, GUO Z G, et al. Study on reinforced soil interface strain softening model in reinforced subgrade slope[J]. Highway Engineering, 2023, 48(2): 68-72, 103.
[5]GURUNG N, IWAO Y, MADHAV M R. Pullout test model for extensible reinforcement[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23(12): 1337-1348.
[6]赖丰文,李丽萍,陈福全.土工格栅筋土拉拔界面的弹性-指数软化模型与性状[J].工程地质学报,2018,26(4):852-860.
LAI F W, LI L P, CHEN F Q. Elastic-exponential softening model for behavior of interface between geogrid reinforcement and soil against pullout[J]. Journal of Engineering Geology, 2018, 26(4): 852-860.
[7]杜常博,易富.筋土拉拔界面弹塑性模型的全过程分析[J].煤炭学报,2020,45(12):4062-4073.
DU C B, YI F. Full-range analysis of elastic-plastic model of pull-out interface between geosynthetics and soil[J]. Journal of China Coal Society, 2020, 45(12): 4062-4073.
[8]WANG J, LIU F Y, WANG P, et al. Particle size effects on coarse soil-geogrid interface response in cyclic and post-cyclic direct shear tests[J]. Geotextiles and Geomembranes, 2016, 44(6): 854-861.
[9]王军,朱晨,刘飞禹,等.法向循环荷载下筋土界面的剪切应力规律及预测[J].岩土工程学报,2022,44(5):954-960.
WANG J, ZHU C, LIU F Y, et al.Shear strength of reinforced soil interface under normal cyclic loading and its prediction[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(5): 954-960.
[10]BASUDHAR P K. Modeling of soil-woven geotextile interface behavior from direct shear test results[J]. Geotextiles and Geomembranes, 2010, 28(4): 403-408.
[11]康博文,周圓兀,王家全,等.基于P5含量的砂砾土与格栅拉拔试验及破坏特性分析[J].广西科技大学学报,2019,30(3):15-21.
KANG B W, ZHOU Y W, WANG J Q, et al. Analysis of pullout test and failure characteristics of gravel soil andgeogrid based on P5 content[J]. Journal of Guangxi University of Science and Technology, 2019, 30(3): 15-21.
[12]刘飞禹,王攀,王军,等.筋—土界面循环剪切刚度和阻尼比的试验研究[J].岩土力学,2016,37(S1):159-165.
LIU F Y, WANG P, WANG J, et al. Experimental research on reinforcement-soil interface stiffness and damping ratio under cyclic shearing[J]. Rock and Soil Mechanics, 2016, 37(S1): 159-165.
[13]丁金华,童军,刘军.新型多功能土-土工合成材料试验机在筋土相互作用研究中的应用[J].长江科学院院报,2017,34(2):29-34.
DING J H, TONG J, LIU J. Application of a multifunctional soil-geosynthetics testing machine to research on soil-geogrid interaction[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(2): 29-34.
[14]WANG Z J, JACOBS F, ZIEGLER M. Experimental and DEM investigation of geogrid-soil interaction under pullout loads[J]. Geotextiles and Geomembranes, 2016, 44(3): 230-246.
[15]王志杰,杨广庆,王贺,等.刚性与柔性顶部边界下筋土界面特性的细观数值研究[J].岩土工程学报,2019,41(5):967-973.
WANG Z J, YANG G Q, WANG H, et al. Mesoscopic numerical studies on geogrid-soil interface behavior under rigid and flexible top boundary conditions[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(5): 967-973.
[16]MIAO C X, ZHENG J J, ZHANG R J, et al. DEM modeling of pullout behavior of geogrid reinforced ballast: the effect of particle shape[J]. Computers and Geotechnics, 2017, 81: 249-261.
[17]PALMEIRA E M. Bearing force mobilisation in pull-out tests on geogrids[J]. Geotextiles and Geomembranes, 2004, 22(6): 481-509.
[18]唐朝生,施斌,高瑋,等.纤维加筋土中单根纤维的拉拔试验及临界加筋长度的确定[J].岩土力学,2009,30(8):2225-2230.
TANG C S, SHI B, GAO W, et al. Single fiber pull-out test and the determination of critical fiber reinforcement length for fiber reinforced soil[J]. Rock and Soil Mechanics, 2009, 30(8): 2225-2230.
[19]徐超,廖星樾.土工格栅与砂土相互作用机制的拉拔试验研究[J].岩土力学,2011,32(2):423-428.
XU C, LIAO X Y. Researches on interaction mechanism between geogrid and sand by pull-out tests[J]. Rock and Soil Mechanics, 2011, 32(2): 423-428.

