基于地基雷达数据构建红松人工林树高、枝下高及接触高模型

刘明睿，贾炜玮

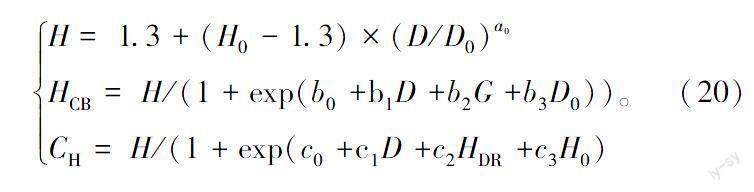
摘要：采用地面激光雷達（Terrestrial Laser Scanning，TLS）扫描10块人工红松林所得到的数据，与实地调查数据相结合，构建红松树高曲线模型、枝下高预估模型与接触高预估模型，并建立联立方程组。首先，从所选择的5种树高曲线模型中，选择出拟合效果较好的2个模型作为联立方程组的备选模型。然后再从5个枝下高基础模型中选出1个拟合效果好，并且适用程度高的模型作为基础模型，运用再参数化和最优子集回归的方法将林分因子（林分平均胸径、林分断面积、高径比、优势木平均胸径和优势木平均高）代入基础模型，选择拟合效果较好的模型作为枝下高备选模型。相同的方法选择拟合效果好的接触高备选模型。最后将树高曲线模型、枝下高备选模型与接触高备选模型分别两两联立，建立联立方程组。通过似不相关回归（Seemingly Unrelated Regression Estimation， SVR或SURE），根据拟合优度与检验结果选择最优秀的方程组，并对联立方程组进行评价。最终得到结果最优联立方程组预估树高时，决定系数R2=0.896，均方根误差RMSE=0.612 m；当方程组预估枝下高时，R2=0.575，RMSE=0.850 m；当方程预估接触高时，R2=0.719，RMSE=0.791 m，而且各种检验指标都较好。综合来看，方程组对树高、枝下高与接触高拟合精度与检验效果较好，可以解决树高、枝下高与接触高的内在相关性问题，为进一步研究红松树冠结构与动态变化提供基础。

关键词：红松人工林；地基雷达；树高模型；枝下高模型；接触高模型

中图分类号：S791.247文献标识码：A文章编号：1006-8023（2024）01-0026-11

Building Tree Height， Height to Crown Base and Crown Contact Height Model for Korean Pine Plantation Based on Terrestrial Laser Scanning Data

LIU MingRui， JIA Weiwei*

（College of Forestry， Northeast Forestry University， Key Laboratory of Sustainable Forest Ecosystem Management， Ministry of Education， Harbin 150040， China）

Abstract：In this paper， data obtained by scanning 10 artificial Korean pine forests based on Terrestrial Laser Scanning （TLS），  were combined with field survey data to construct tree height curve model， height to crown base prediction model and crown contact height prediction model， and a simultaneous equation system was established. First， from the five kinds of tree height curve models selected， two models with better fitting effects were selected as the candidate models of the simultaneous equations. Then one model with good fitting effect and high applicability from the five height to crown base models was selected as base model， and the stand factors （mean DBH of stand， stand basal area， ratio of height to diameter， mean DBH of dominant trees and mean height of dominant trees） were introduced into the basic model by means of re-parameterization and optimal subset regression， the model with better fitting effect was selected as the alternative model of height to crown base model. The same method was used to select alternative crown contact height model with good fitting effect. Finally， the tree height curve model， alternative height to crown base model and alternative crown contact height model were combined in pairs to establish simultaneous equations. Through seemingly unrelated regression estimation， the best equations were selected by the goodness of fit and the test results， and the simultaneous equations were evaluated. When the optimal simultaneous equation was used to estimate the tree height， the decision coefficient R2 =0.896， and the root mean square error RMSE=0.612 m; when the equations was used to estimate the height to crown， R2=0.575， RMSE=0.850 m; when the equations was used to estimate the crown contact height， R2=0.719， RMSE=0.791 m， and all kinds of inspection indexes were good. On the whole， the equation system had better fitting accuracy and test effect for tree height， height to crown and crown contact height， and can solve the internal correlation problem of tree height， height to crown and crown contact height， which provided the basis for further study of crown structure and dynamic changes of Korean pine.

Keywords：Korean pine plantation; Terrestrial Laser Scanning; tree height model; height to crown base model; crown contact height model

0引言

红松是东北地区主要的林木装饰和木材生产树种之一。但是，其木材质量和生长能力在很大程度上受树冠尺寸、结构和形状的影响。为了更好地估测林分树冠，对该树种进行了相关研究，在进行大量数据分析的基础上，通过对模型的比较，最终选择出估测树高、枝下高（Height to crown base， HCB）与接触高（Crown Contact Height， CH）的最优模型[1]。树高是决定树木总体积和生物量的关键因素，并且是反映森林立地质量的重要指标[2]。树冠的大小也可以反映树木的光合作用能力。有效冠[3]作为树木光合作用的主要部分，其作用更加重要，高度和树冠大小结合在一起，在确定林分的总叶面积方面起着重要的生理作用[4]。在森林资源调查中，影响森林生长的因素很多，如胸径、树高、枝下高、活枝高、郁闭度、木材产量、年龄、地位、立地条件和产地等，但最重要的是树高和胸径，这也是衡量森林生长的2个重要指标[5]。并非所有活枝对树干的生长均有贡献，部分处于树冠下部的活枝，由于受到上层枝叶或相邻木的遮挡，其合成的光合产物仅能满足自身的生长和呼吸，并没有额外的光合产物提供给树干生长[6]。Hackenberg等[7] 采用变指数方程模拟树冠的“阳冠”部分，并假定“阴冠”半径为一个常数。随后，也有部分学者基于相同的原则，通过分析树干断面积增长量在垂直方向的分布规律将树冠划分为“阳冠和阴冠”[8] 或“有效冠和无效冠”。本研究的接触高模型可以间接地表示有效冠高。

在传统林业调查中胸径测定简单方便，精度高，然而与胸径指标相比，树高、枝下高和接触高的测定却费时耗工，误差难以控制，这就给林业生产与实践带来较大困难。为此，通过假设胸径－树高/枝下高/接触高某些关系模型，由胸径估测树高、枝下高，有效冠高对森林调查具有十分重要的意义。传统林业提取树高、枝下高与接触高都需要人工实地单木检测，而详细的每木检尺既费时又费力的，最近几年许多学者提出了运用地基雷达（Terrestrial Laser Scanning， TLS）可以自动检测树干。TLS是生产和分析森林调查数据的新技术。通过高分辨率的三维数据，TLS采集具有提高信息质量的巨大潜力。传统林业调查，许多树干数据是通过相对有限的现场数据和预先存在的模型来估算的，或是通过对树木进行砍伐，然后进行单木检测来计算的。与传统林业调查相比，TLS系统具有自动、非破坏性和快速产生大量与树木的结构和生物物理指标有关的准确数据的功能 [9-10]。利用这种新兴技术，TLS数据成功应用于单棵树，样地和林分级别的各种估测，例如直径、树干曲线和高度测量、树冠宽度估计、体积和生物量计算、树种检测[9， 11]。重复TLS测量还可用于变化检测目的，例如评估增加的体积或生物量[12]。本研究以红松人工林为研究对象，采用地基雷达（TLS）扫描所获得的点云数据，提取树高、枝下高、接触高和胸径，主要从3个方面进行研究：1）选取最优的树高和枝下高模型，建立新的接触高模型；2）在最优模型的基础上，建立树高模型、枝下高模型与接触高模型的联立方程组；3）对树高模型、枝下高模型、接触高模型、联立方程组模型进行评价[13]。

1研究区域与研究方法

1.1研究区域概况

研究区位于黑龙江省佳木斯市桦南县孟家岗林场，孟家岗林场位于桦南县东北部，地理坐标为130°32′42″～130°52′36″ E46°20′～46°30′50″ N，地处完达山西麓余脉，以低山丘陵为主，平均海拔为250 m，最高山峰为老平岗，其海拔575 m。水系属松花江支流体系，最大的河流是柳树河，为三级支流。属东亚大陆性季风气候。冬季漫长，寒冷干燥；夏季短暂，温暖潮湿；早春少雨，大风易旱；秋季气温下降迅速，常造成冻害。初霜在9月上旬和中旬，晚霜在5月中旬和下旬。年平均气温为2.7 ℃。极端最高气温35.6 ℃，最低气温-34.7 ℃。年积温为2 547 ℃。年平均降水量550 mm。全年日照充足，时数为1 955 h。无霜期在120 d左右。

1.2数据来源及处理

数据为2019年3月中旬用扫描仪Trimble TX8扫描的10块红松人工林样地图像，共计548棵红松样木。用Lidar360软件，将配准后的点云进行去噪、地面点分类和归一化等一系列处理，提取样地树木的树高、胸径、坐标、冠幅、树冠直径、树冠体积、枝下高、最低接触高和最高接触高等数据。

将地基雷达扫描的数据与人工样地每木检尺的数据结合、处理、汇总，得到表1。

1.3研究方法

1.3.1树高曲线模型

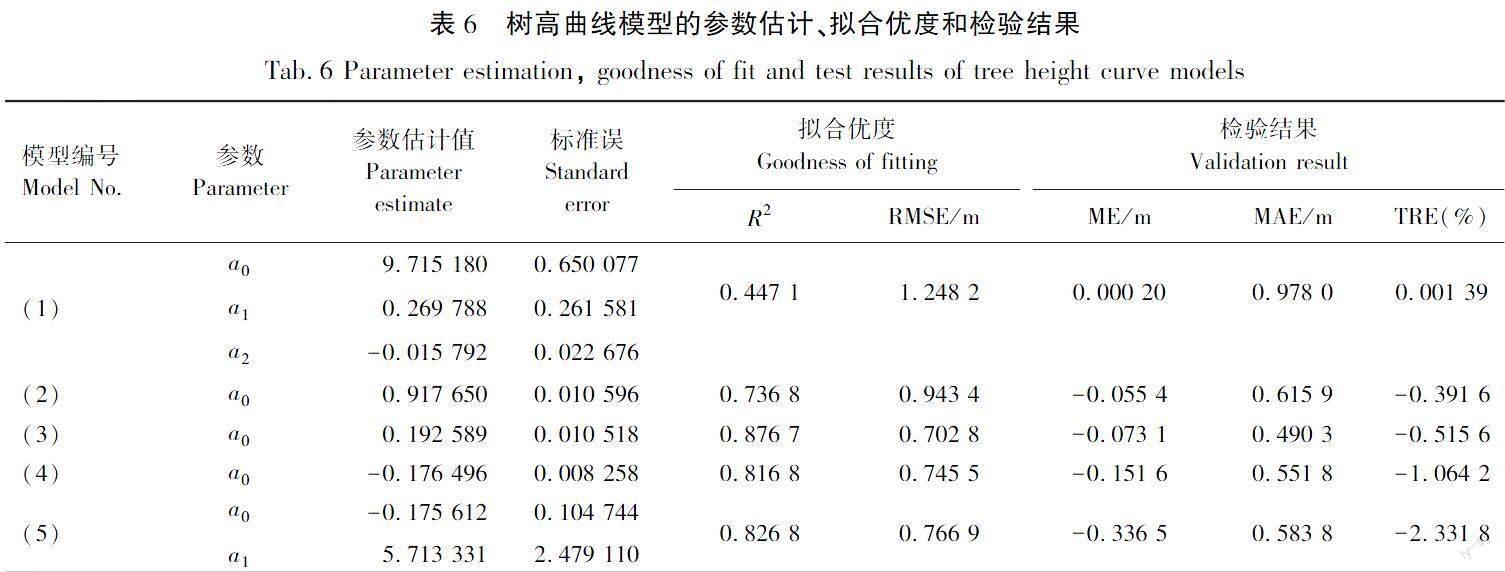
树高曲线模型有几十种，选取其中5种拟合精度较高且具有丰富的生物学意义的树高曲线模型作为本次红松人工林试验的备选模型，见表2。

1.3.2枝下高模型

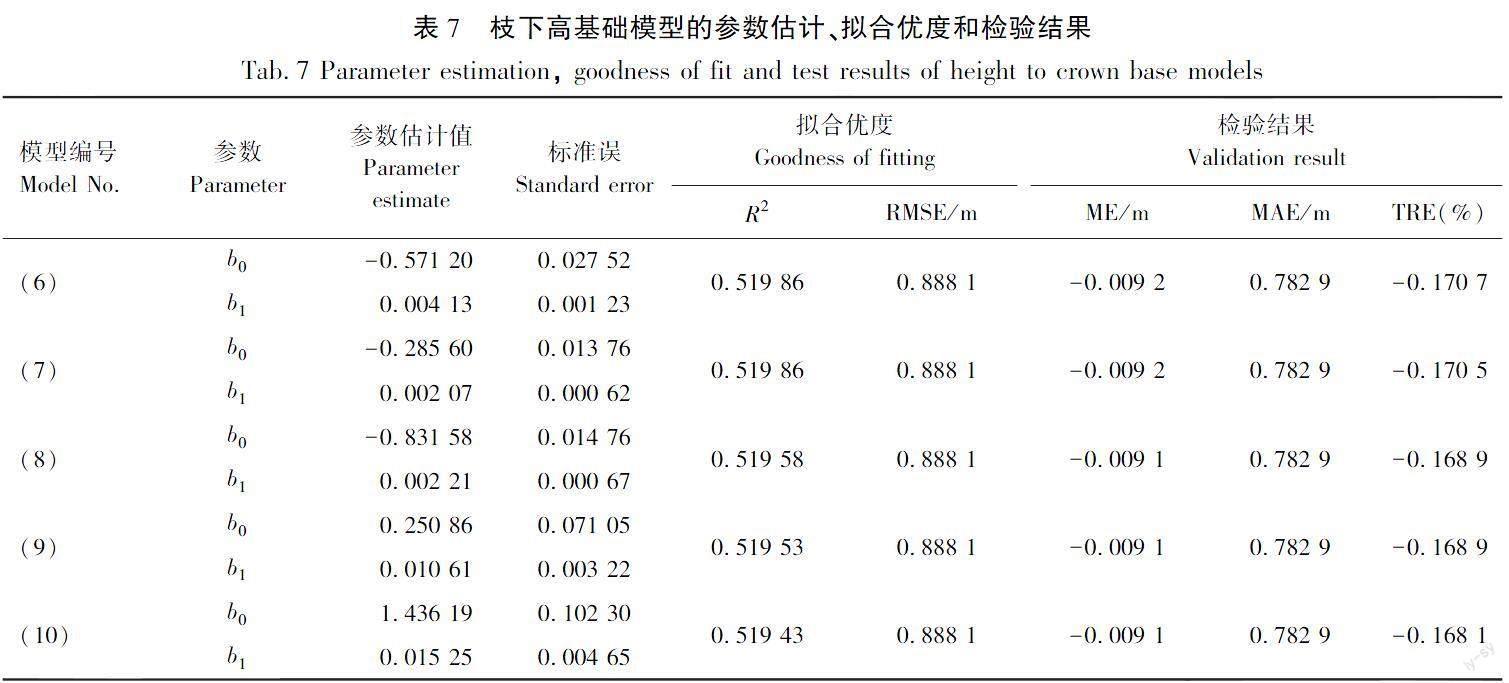
枝下高模型主要有2种形式，Logistic形式和指数形式，本次试验采取5个方程为基础方程，见表3。许多研究表明，树高（H）是预测枝下高的第1变量，胸径（D）是预测枝下高的第2变量。因此，本研究首先用H和D（X=b0+b1×D，b0、b1为参数）自变量拟合模型，选择最优模型。由于竞争因素（COMP）和立地条件（SITE）还会影响枝下高，通过模型再参数化引入了反映这些条件的变量。采用最優子集回归方法对变量进行筛选，建立了几个拟合效果较好的模型作为方程组中枝下高的备选模型。

X的表达参数为

X=b+cSIZE+dCOMP+eSITE

式中：b、c、d、e为模型参数;SITE为立地条件函数；COMP为竞争因子函数；SIIE为林分大小函数。

林分大小函数：SIZE=f（Dg，H）

竞争因子函数：COMP=f（G，HDR）

立地条件函数：SITE=f（H0，D0）

式中，HDR为高径比。

1.3.3接触高模型

接触高模型与枝下高模型形式应该近似，所以参考枝下高模型，见表4，将接触高（式中记为CH）模型也分为2种形式，Logistic形式和指数形式。首先只拟合含林木因子作为自变量的接触高模型，选出最优的基础模型。通过再参数化的方法，在最优基础模型中引入林分属性因子和竞争属性因子，利用SAS9.4软件分别拟合各种不同变量组合下的接触高模型，建立多个拟合效果较好的接触高模型，最终选择出最佳的接触高模型。

林分大小函数：SIZE=f（D0，H，CL，CW）

竞争因子函数：COMP=f（G，HDR）

立地条件函数：SITE=f（H0，D0）

式中：CL为冠长；CW为冠幅。

1.3.4联立方程组

由于树高、枝下高与接触高存在高度的内在相关性，采用最小二乘法估计3个模型参数，满足不了误差同时最小的条件。可通过最优子集回归的方法，选择最优的树高曲线模型、枝下高模型和接触高模型，建立联立方程组。如果多方程间有联系，同时估计这些方程可提高估计效率，称为“系统估计（system estimation）”。多方程联合估计的缺点是，如果某方程误差较大，将污染整个方程系统。选择单一方程估计或系统估计，也是“有效性”与“稳健性”的权衡。多方程系统主要分为2类。一类为“联立方程组（simultaneous equations）”，即不同方程间存在内在联系，一个方程的解释变量是另一方程的被解释变量。另一类为“似不相关回归（Seemingly Unrelated Regression Estimation，SUR或SURE）”，即各方程的变量之间没有内在相关性，但各方程的扰动项之间存在相关性。因此树高曲线模型、枝下高模型与接触高模型就采用似不相关回归来建立方程组。

联立方程组通式

H=∫（SIZE，COMP，SITE）

HCB=∫（H，SIZE，COMP，SITE）

CH=∫H，SIZE，COMP，SITE

式中：H、HCB、CH为内生变量;SIZE、COMP、SITE 为外生变量。

1.3.5模型的评价与检验

回归分析的最后也是最重要的一步，是充分验证所选模型。本次试验利用决定系数（R2）和均方根误差（RMSE）来评价模型的拟合效果。用平均误差（ME）、绝对误差（MAE）、总相对误差（TRE）对模型进行了检验。其中，ME和MAE用于反映绝对误差，TRE用于反映相对误差。每个测试指标的值越小，模型的誤差越小。

2结果与分析

2.1地基雷达数据的精度

通过Lidar360处理得到的雷达数据与人工每木检尺所得到的样地数据进行对比，得到表5。结果显示胸径与树高的精度都在95%左右，而活枝高的精度也达到了85%左右，得到的精度可以确保地基雷达提取的数据能应用到模型构建中。

总体来看TLS对胸径估计偏低，偏差小于0，胸径的偏差可能是由于扫描数据噪点或者后期处理软件本身所产生的偏差，因为胸径的提取是Lidar360软件自动提取的，而对枝下高的估计偏高，偏差大于0，枝下高是人工测量的，可能产生测量误差，并且由于点云数据只能对树木枝条的轮廓进行全面的扫描，但是无法分辨是活枝还是死枝，只能凭借枝条的形态和生长角度，还有是否有叶，自己进行判断，也会产生误差。而对树高的估计值偏低，偏差大于0，这与其他学者的研究结果相似[20-21]。但是总体的检测结果还不错，精度都在可以接受的范围内。可以代表人工红松林的大体数据。

通过对树高与枝下高数据的精度检验，证明TLS数据在高度方面提取的精度很高，可以代表实际数据运用于建模之中，所以用TLS提取的接触高数据也应该可以应用到实际应用与构建模型之中。

2.2树高曲线模型的选取

利用TLS提取的数据与实地测量数据相结合，对表2中5种树高曲线模型进行拟合，表6为树高曲线模型参数估计值、拟合优度和检验结果。以往实验证明Lidar数据往往会低估树高值[20-22]。由表4可知，R2在0.44～0.88，并没有0.9以上的，可能是由于样本太少，应增加样本量。模型（1）拟合优度与检验结果相比，其他4个模型相对较差，并且是多参数模型，应用也比较复杂。而模型（3）、模型（4）、模型（5）拟合优度与检验结果都比较理想，结果也相差不明显。所以综上所述，将模型（3）和模型（5）作为树高曲线模型的备选模型。

2.3枝下高模型的选取

首先拟合只含有树高（H）和胸径（DBH）作为自变量的枝下高模型（X=b0+b1×D，b0、b1为参数），然后选出最优秀的枝下高模型。其中将模型参数k、m、w分别设置为1、2、3，结果见表7。拟合结果的决定系数R2都不高，都在0.5左右，可能是由于建模数据相对较少，不能准确地预测枝下高模型，而且模型（6）、模型（7）、模型（8）的因变量范围无法限定在（0，H）之间，并不具备生物学意义。从检验结果来看，所有模型对枝下高（HCB）都相对高估（ME＜0），TRE＜-0.2%，证明拟合效果很好。模型（9）与模型（10）相差不大，但是模型（10）带了指数形式，在实际应用中，如果结果没有明显差距，相对简单的模型可以更好地运用在生产实践当中，所以本研究选择模型（9）作为枝下高基础模型的备选模型。

将林分因子SIZE、COMP、SITE进行再参数化函数代入模型（9）中，采用最优子集回归法拟合参数模型。运用最优子集回归法拟合结果差异不大，决定系数R2都在0.52～0.59，RMSE大多数都在0.88左右，ME在-0.01以下，MAE在0.7～0.8，TRE在-0.15%～-0.13%，总的来说差异不大，拟合效果都很好，但还是有些高估枝下高（ME＜0）。通過再参数化和最优子集的方法，将林分因子代入枝下高基础模型，提高了决定系数R2，降低了RMSE，总的来说提高了模型的拟合精度，使模型的拟合效果更佳。

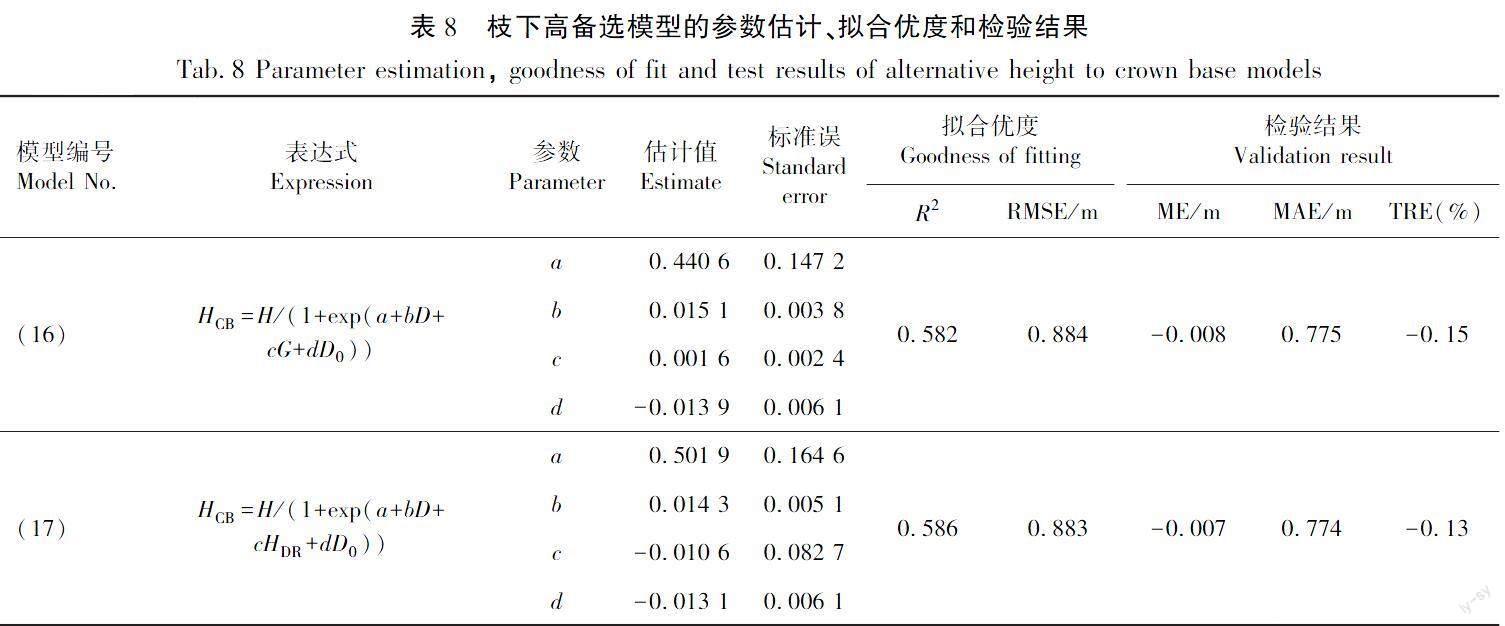
林分断面积（G）、高径比（HDR）都是林分的竞争因子，将2个变量分别拟合到枝下高的备选模型当中。优势木平均胸径（D0）和优势木平均高（H0）代表了林分的立地条件，与优势木的平均高（H0）相比，优势木平均胸径（D0）在模型当中的拟合精度更好。决定系数R2相对更高，所以把林分断面积（G）、高径比（HDR）与优势木平均胸径（D0）分别加入到枝下高备选模型当中，结果见表8。

由表8可知，2个备选模型的决定系数R2都在0.58左右，RMSE结果都在0.88左右，都会高估枝下高（ME较小，而且都小于0），平均绝对误差（MAE）在0.77左右，平均预估误差TRE都小于-0.16%。总体来说拟合效果较好。

图1（a）、图1（b）为公式（16）的残差值正态分布、预测值与残差分布，图1（c）、图1（d ）为公式（17）的残差值正态分布、预测值与残差值。从图1中可以看出，残差值属于正态分布，残差的散点是随机的，说明模型的拟合效果很好，无异方差现象。

2.4接触高模型的选取

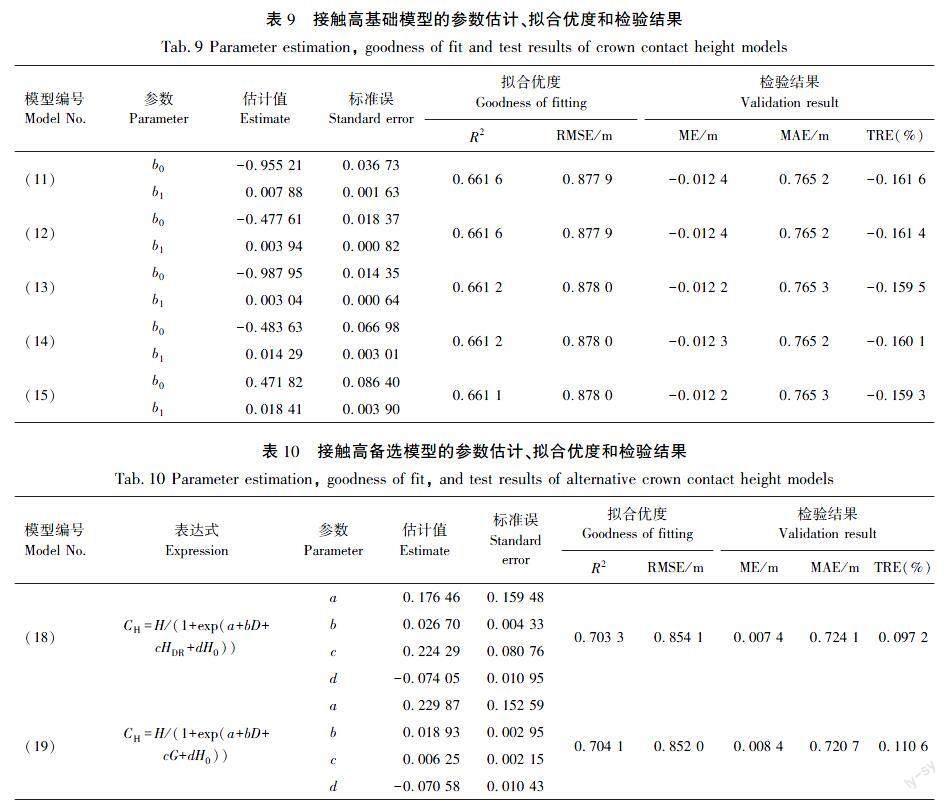
接触高模型的选取与枝下高模型选取相同。结果见表9。拟合结果的决定系数R2都在0.66左右，与枝下高基础模型选取相似，在实际应用中，如果结果没有明显差距，相对简单的模型可以更好地运用在生产实践当中，所以本研究选择模型（14）作为接触高基础模型的备选模型。

同样将模型（14）进行再参数化，将林分因子SIZE、COMP、SITE函数代入模型（14）中，决定系数R2都在0.7左右，RMSE大多数都在0.878左右，ME在0.01以下，MAE在0.71～0.73，TRE在0.09%～0.11%。通过再参数化和最优子集的方法，将林分因子代入接触高基础模型，提高了决定系数R2，降低了RMSE，提高了模型的拟合精度，模型的拟合效果更佳。

林分断面积（G）、高径比（HDR）都代表了林分的竞争因子2个变量分别拟合到枝下高的备选模型当中。优势木平均胸径（D0） 和优势木平均高（H0）代表了林分的立地条件，与枝下高模型相反，在接触高模型中，优势木的平均高（H0）比优势木平均胸径（D0）在模型当中的拟合精度更好。决定系数R2相对更高，所以把林分断面积（G），高径比（HDR）与优势木的平均高（H0）分别加入到接触高备选模型当中，结果见表10。

由表10可知，2个备选模型的决定系数R2都在0.7左右，RMSE结果都在0.85左右，ME都小于0.01，平均绝对误差MAE在0.72左右，平均预估误差MPE都小于0.02%。总体来说拟合效果较好。

图2（a）、图2（b）是公式（18）的残差值正态分布、预测值与残差分布，图2（c）、图2（d）为公式（19）的残差值正态分布、预测值与残差值。从图2中可以看出，残差值属于正态分布，残差的散点是随机的，说明模型的拟合效果很好，并且没有出现异方差等问题。

2.5联立方程组

将备选的树高曲线模型（模型（3）、模型（5）），枝下高备选模型（模型（16）、模型（17））与接触高备选模型（模型（18）、模型（19））分别联立，建立联立方程组。采用似不相关回归（SUR）来拟合方程组，但是拟合过程中发现，由于树高、枝下高与接触高存在高度的内相关性，大多数方程组存在多重共线性，无法拟合出可靠的方程组。只有应用模型（3）、模型（16）和模型（18）联立方程组不存在多重共线性，可以得出相对可靠的联立方程组。方程组形式如下

H=1.3+（H0-1.3）×（D/D0）a0

HCB=H/（1+exp（b0+b1D+b2G+b3D0））。

CH=H/（1+exp（c0+c1D+c2HDR+c3H0）（20）

图3为当立地条件与竞争条件相同时（林分因子都采用平均林分因子），树高、枝下高和接触高分别与胸径的关系曲线。空间上，从上到下依次为树

高、接触高和枝下高，与实际情况符合。随着胸径的不断增大，树高也不断地增加，树木越粗树高越高。但是胸径增大到一定的程度后，接触高与枝下高都会相对减小，也就是说当树木越粗，成长的越好，树木的冠就越大，有效冠也越大，与实际情况也相符。说明联立方程组不仅解决了树高、枝下高和接触高的内在相关性，也拥有较高的预测能力。

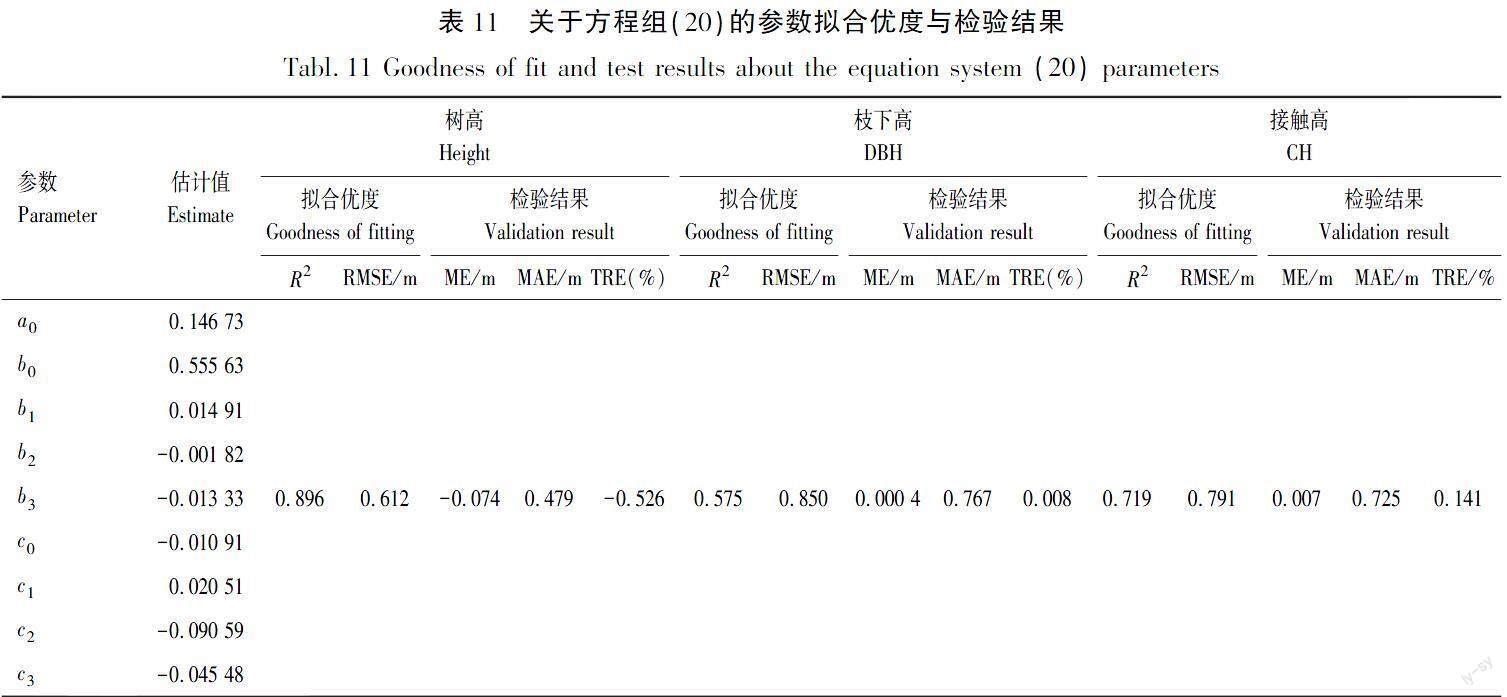
由表11可知，方程组中，树高模型拟合优度R2与RMSE都相对提高，R2从0.876上升到0.896，RMSE也从0.702下降到了0.612，检验精度在原有的基础上上下波动幅度很小，都在千分位上波动。枝下高模型虽然拟合优度R2有所降低，从0.582降低到0.575，但是检验精度有了很大的提升，ME从-0.008降低到了0.000 4，前进了一个数量级。接触高模型在方程组中拟合优度和检验结果都相对有所提升。综合来看方程组比独立模型预估的结果误差更小，模型预估精度更高。

3结论与讨论

3.1结论

本研究采用TLS提取的树高、胸径、枝下高数据与实地测量的相关数据相结合，无损地测量了位于孟家岗林场的10块红松人工林，并建立了树高曲线、枝下高与接触高基础方程，采用似不相关回归建立了联立方程组，成功拟合出最优联立方程组模型。当单独建立树高曲线、枝下高模型与接触高模型时，结果分别为：

1）树高曲线的决定系数R2为0.8左右，均方根误差（RMSE）为0.7 m左右。

2）枝下高再参数化模型决定系数R2为0.58左右，均方根误差（RMSE）在0.88 m左右。

3）接触高再参数化模型决定系数R2在0.7左右，均方根误差（RMSE）为0.85 m。

4）当建立联立方程组预估树高时，决定系数R2为0.896，均方根误差（RMSE）为0.612 m；当方程组预估枝下高时，决定系数R2为0.575，均方根误差（RMSE）为0.850 m，预估接触高时决定系数R2为0.719，均方根误差（RMSE）为0.791 m，拟合优度和检验指标都有所提高并且各种检验指标都较好。

通过本次试验可以得出结论：TLS调查可以与传统调查方法相结合，TLS数据可以运用到模型构建的过程中，模型的再参数化，不仅提高了模型的精度，也将林分因子、立地条件等变量充分考虑。通过联立方程组的方式，不仅解决了模型的内在相关性问题，也保证了模型具有较高的预测能力。

3.2讨论

联立方程组中各项系数所代表不同的含义，其中代表胸径前的参数b1、c1为正数，说明胸径与枝下高呈现正相关，但是枝下高与接触高模型都是分数形式，当胸径不断增大的时候，分子树高曲线模型的增长比例比分母增长比例小，即树木越大枝下高与接触高越低。这与李想[23]建立的樟子松相关的枝下高模型，所得到的结果一致。当树木生长较好的时候，竞争压力就小，自然整枝能力就差，所以死枝就相对较少，第一活枝相对较低，树冠呈現塔状，所以枝下高就相对较低。而代表竞争因子林分断面积的参数b2、c2为负数，即竞争越激烈，枝下高越高，自然整枝效果越大，死枝就越多，第一活枝相对就越高，枝下高也就越高。接触高的确定，可以间接确定有效冠的高度，为人工整枝、抚育间伐提供一定理论基础。对森林质量、碳储量的提升提供一定的帮助。

通过本次实验，TLS数据可以更广泛地应用到从前需要大量人工测量数据的试验当中，为以前费时费力的数据收集工作提供了新的途径。但是TLS数据与实测数据仍然有些偏差，例如在本次试验中，枝下高的提取，由于点云数据只能对树木枝条进行全面的扫描，但是无法分辨是活枝还是死枝，只能凭借枝条的形态和生长角度判断第一活枝高，主观进行判断，就会产生误差。在以后的试验中最好是TLS数据与实测数据相结合，提供更精确更全面的数据支持试验结论。

【参考文献】

[1]王佳燕.海南东寨港几种红树植物主要生长特征因子间的关系研究[D].海口：华南热带农业大学，2007.

WANG J Y. Studies on the relationships among the main growth characteristics of mangrove plants in Dongzhai port， Hainan province[D]. Haikou： South China Agricultural University， 2007.

[2]ASSMAN E， ASSMAN E. The principles of forest yield study[J]. Forest Science， 1970（4）： 498-498.

[3]李凤日，王治富，王保森.落叶松人工林有效冠动态研究：有效冠的确定[J].东北林业大学学报，1996，24（1）：1-8.

LI F R， WANG Z F， WANG B S. Study on dynamics of effective crown of larch plantation： Determination of effective crow[J]. Journal of Northeast Forestry University， 1996， 24（1）： 1-8.

[4]RUSSELL M B， WEISKITTEL A R， KERSHAW J A. Comparing strategies for modeling individual-tree height and height-to-crown base increment in mixed-species Acadian forests of northeastern North America[J]. European Journal of Forest Research， 2014， 133（6）： 1121-1135.

[5]顾凤岐，王艳.基于红松胸径与树高相关模型的研究[J].森林工程，2013，29（4）：41-43.

GU F J， WANG Y. Study on the correlation model between DBH and tree height of Pinus koraiensis[J]. Forest Engineering， 2013， 29（4）： 41-43.

[6]HOSOI F， OMASA K. Voxel-based 3-D modeling of individual trees for estimating leaf area density using high-resolution portable scanning lidar[J]. IEEE Transactions on Geoscience & Remote Sensing， 2006， 44（12）： 3610-3618.

[7]HACKENBERG， J SPIECKER， H CALDERS， et al. Simple Tree-an efficient open source tool to build tree models from TLS clouds[J]. Forests， 2015， 6（11）： 4245-4294.

[8]AKERBLOM M， RAUMONEN P， MAKIPAA R， et al. Automatic tree species recognition with quantitative structure models[J]. Remote Sensing of Environment， 2017， 191： 1-12.

[9]RAUMONEN P， KAASALAINEN M， AKERBLOM M， et al. Fast automatic precision tree models from terrestrial laser scanner data[J]. Remote Sensing， 2013， 5： 491-520.

[10]MOLLER C M. The influence of pruning on the growth of conifers[J]. Forestry， 1962， 33（1）： 37-53.

[11]RAULIER F， UNG CH， OUELLET D. Influence of social status on crown geometry and volume increment in regular and irregular black spruce stand[J]. Canadian Journal of Forest Research， 1996， 26（10）： 1742-1753.

[12]王迪生，宋新民.一个新的单木竞争指标-相对有效冠幅比[J].林业科学研究，1994，7（3）：337-341.

WANG D S， SONG X M. A new single tree competition index-relative effective crown width ratio[J]. Forestry Scientific Research， 1994， 7（3）：337-341.

[13]李想.黑龙江省人工樟子松枝下高动态预测模型的研究[D]. 哈尔滨： 东北林业大学， 2018.

LI X. Study on the dynamic prediction model of the height under the branch of Pinus sylvestris var. mongolica in Heilongjiang province[D]. Harbin： Northeast Forestry University， 2018.

[14]SHARMA M， YIN ZHANG S. Height-diameter models using stand characteristics for Pinus banksiana and Picea mariana[J]. Scandinavian Journal of Forest Research， 2004， 19（5）： 442-451.

[15]MONNESS E. Diameter distributions and height curves in even-aged stands of Pinus sylvestris L.[J]. Norsk Institutt for Skogforskning， 1982， 36（15）： 1-40.

[16]SANCHEZ C A L， VARELA J G， DORADO F C， et al. A height-diameter model for Pinus radiata D. Don in Galicia （Northwest Spain）[J]. Annals of Forest Science， 2003， 60（3）： 237-245.

[17]WYKOFF W R. User's guide to the stand prognosis model[R].  U.S. Department of Agriculture， Forest Service， Intermountain Forest and Range Experiment Station， 1982： 112.

[18]WALTERS D K， HANN D W. Taper equations for six conifer species in southwest Oregon[M]. Corvallis： Oregon State University， 1986.

[19]KERSHAW J A， MAGUIRE D A， HANN D W. Longevity and duration of radial growth in Douglas-fir branches[J]. Canadian Journal of Forest Research， 1990， 20（11）： 1690-1695.

[20]POPESCU S C， WYNNE R H， NELSON R F. Estimating plot-level tree heights with Lidar： local filtering with a canopy-height based variable window size[J]. Computers & Electronics in Agriculture， 2002， 37（1/3）： 71-95.

[21]CHEN Q， BALDOCCHI D， GONG P， et al. Isolating individual trees in a savanna woodland using small footprint Lidar data[J]. Photogrammetric Engineering & Remote Sensing， 2006， 72（8）： 923-932.

[22]付玉嬪，孟梦，姜远标，等.思茅松育苗试验及造林后效果分析[J].西部林业科学，2022，51（3）：11-17.

FU Y B， MENG M， JIANG Y B， et al. Experimental research on seedling cultivation of Pinus kesiya var. langbianensis[J]. Journal of West China Forestry Science， 2022， 51（3）：11-17.

[23]李想，董利虎，李凤日.基于联立方程组的人工樟子松枝下高模型构建[J].北京林业大学学报，2018，40（6）：9-18.

LI X， DONG L H， LI F R.Building height to crown base models for Mongolian pine plantation based on simultaneous equations in Heilongjiang Province of northeastern China[J]. Journal of Beijing Forestry University， 2018， 40（6）： 9-18.