基于响应面分析的淹没水射流破土施工参数优化设计
邱玥钦,蓝雄东,刘剑,王观石,罗嗣海
1.江西理工大学土木与测绘工程学院,江西赣州 341000;2.赣南科技学院资源与建筑工程学院,江西赣州 341000
稀土作为我国重要的战略资源之一,被誉为“工业维生素”“新材料之母”[1-2]。随着科技的发展,稀土矿的开采目前已进步至第三代原地浸矿工艺,但其收液系统仍存在一些问题,主要是离子型稀土矿原地浸矿工艺收液系统,常采用巷道与导流孔的形式来收集稀土母液。巷道对稀土资源的浪费较大,而现有的导流孔收液范围又较小,当遇到底板破碎带时,收液效率会大幅度降低。水射流开采技术拥有无污染、反作用力小、冲蚀钻孔效率高、没有热反应区、对材料要求不高等优点,现已被运用到煤矿开采、石油钻井和地下工程等方面[3-5]。近年来,有学者借鉴水射流技术在煤矿开采中的应用成果,考虑将水射流技术应用于离子型稀土矿导流孔内部侧向增孔,以扩大导流孔收液范围。此技术的关键在于射流孔的深度及径宽,射流孔的深度直接影响收液范围,射流孔径宽则影响其稳定性。因此,选取合适的施工参数提高射流孔深度的同时兼顾其稳定性,是离子型稀土矿侧向增孔技术的关键。
目前,淹没水射流破土深度优化设计的研究相对较少,大多利用正交实验寻求最优施工参数[6]。但正交实验具有一定的局限性,采用正交实验考虑因素间的相互作用时工作量会非常大,且在指定的整个区域无法获得实验因素与响应目标值之间明确的函数关系式。响应面法(Response Surface Method,RSM)是数学与统计学相结合的产物,能用少量实验数据建立多个因素与一个或多个响应值之间的数学模型,并评估各因素及各因素间的交互作用对响应值的影响。响应面法能够很好地解决多因素、多水平下的连续响应问题,与正交实验相比具有实验次数少、成本低、精度高、更加全面等优势[7-8]。
很多学者使用响应面法进行优化设计。党菁等[9]通过响应面的Box Behnken Design(BBD)建立了接头静力强度与各参数之间的二次回归多项式,得出了板材无铆钉滚压连接接头的最优工艺参数。温震江等[10]通过响应面的BBD 模型对矿渣胶凝材料复合激发剂配比进行设计,得到了各因素交互作用对3 个响应值的影响,并结合满意度函数对矿渣胶凝材料复合激发剂配比进行多目标优化,进而得到了矿渣胶凝材料复合激发剂配比3 因素3 响应值的综合最优配比。胡亚飞等[11]利用响应面的中心复合设计对混合骨料填充体强度发展进行实验设计,利用响应面-满意度函数(RSM-DF)多目标优化法对配合比进行优化设计,得到了满足要求的最佳配比。
本文基于任意拉格朗日-欧拉方法(Arbitrary Lagrange Euler,ALE),建立淹没水射流破土的数值计算模型,以喷嘴直径、射流靶距及射流压力为因素,以射流孔深度及径宽作为响应值建立响应面分析模型,研究了各因素交互作用下对响应值的影响规律,并结合满意度函数对破土施工中的射流参数进行优化设计,获得不同破土深度下的最佳施工参数,为淹没水射流破土施工参数的优化设计提供参考。
1 数值计算模型
1.1 数值计算方法
数值模拟是研究水射流的重要手段,采用ALE方法对淹没状态下水射流破土的过程进行数值仿真计算。ALE 方法通过将欧拉法和拉格朗日法相结合,可以在固体和流体之间建立联系,实现流固耦合计算[12-13]。该方法克服了纯欧拉法中网格始终保持最初空间位置不变的问题,同时也解决了纯拉格朗日法出现的网格畸变问题,且ALE 流固耦合罚函数算法能够在解决流固耦合及大变形问题的同时,精确定位从物质和主物质之间的相对位移,保证计算过程的收敛度和精确度[14-15]。
1.2 几何模型
理想情况下淹没水射流冲蚀土体过程是呈轴对称的,故采取1/4 建模。数值模型由射流源、水域和土体组成,采用ALE 方法,只需将空气区域设定为水即可实现淹没射流,水区域只有在射流破土时土壤向两边堆砌,才会对破土过程产生影响。模型上部为射流源和水域,下部为土体,土体尺寸为100 mm×100 mm×250 mm,射流源和水域采用的是ALE 网格算法,土体则采用Lagrange 网格算法。数值计算过程中水射流运动有较明显的局部效应,因此对射流源和射流接触部位进行网格细化处理[14],水射流破土模型如图1 所示。

图1 水射流破土模型Fig.1 Water jet breaking model
1.3 材料参数
射流域与水域通过MAT_NULL 空材料模型来设置。土体材料使用MAT_147 材料,该材料模型中基本包含了土体特性相关的所有基本参数,如密度ρ、含水率ω、剪切模量G、体积模量K、黏聚力C、内摩擦角φ等。参数测量方法及具体取值列于表1。其中,剪切模量通过微型十字板剪切仪测得,体积模量通过旁压仪测得,黏聚力和内摩擦角通过英国GDS 公司的饱和-非饱和应力路径三轴仪实验系统测得。由于MAT_147 材料本构模型中没有失效准则,如果直接运算则会引起网格畸变最终导致计算失败,因此需要添加侵蚀算法,通过添加关键字MAT_ADD_ERODION 引入侵蚀算法,该算法包含网格失效准则。

表1 土体材料参数Table 1 Material parameter of soil
1.4 数值模型验证
数值模型建立后需要对模型进行实验验证。水射流实验装置如图2 所示,包括实验土箱、升降支架、射流供压及监测控制4 部分。其中,实验土箱由500 mm×200 mm×500 mm(长×宽×高)的有机玻璃箱组成;升降支架由铝合金组成,用以调整射流靶距;射流供压模块由圆形塑料水箱、圆形喷嘴、高压泵组成;监测控制模块则由电磁流量计、调压阀及压力变送器组成。
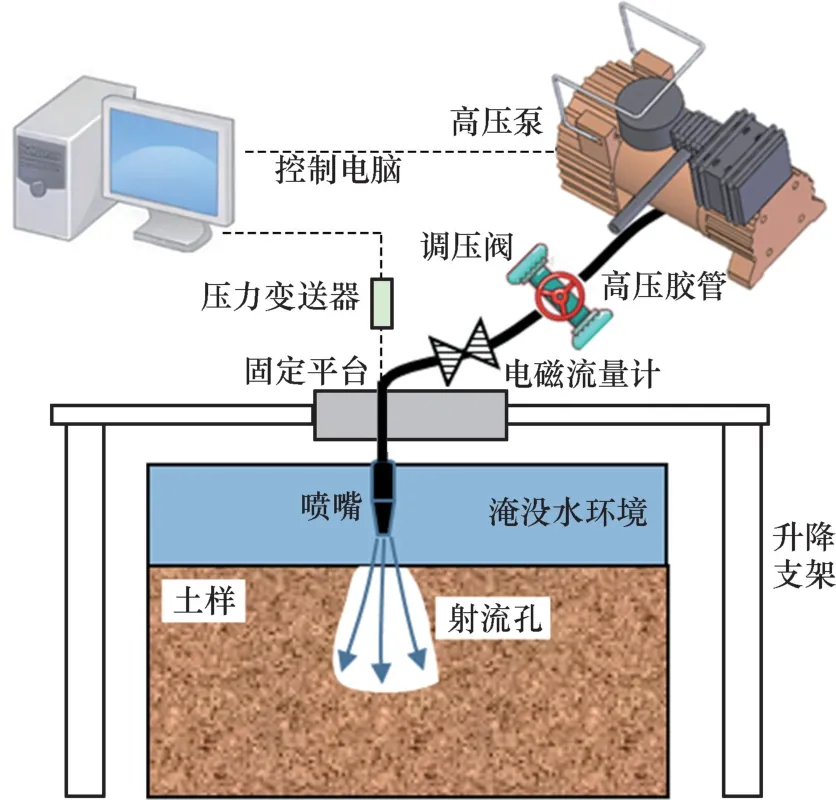
图2 水射流实验装置Fig.2 Experimental equipment of water jet breaking soil
实验步骤:
(1) 通过升降支架调整射流靶距;
(2) 向土箱中加入适量的水,营造稳定的淹没射流环境;
(3) 通过调压阀调整高压泵压力,射流压力通过压力变送器监测,射流流量通过电磁流量计监测,换算得到喷嘴初始流速;
(4) 射流结束后,排出土体上部的淹没水,使用注浆器向射流孔中灌满调制好的石膏浆;
(5) 待石膏凝固后,拆除实验箱体侧壁,仔细挖出射流孔的石膏固结体,分析射流孔的尺寸和形状。
选取射流压力7.2 MPa、喷嘴直径1 mm、靶距3 cm 的实验工况,进行数值模拟验证。图3 为实验与模拟射流孔形态对比图。结果表明:模拟的射流孔更深,宽度更小,这是由于模拟中并未考虑变形速率对土体强度的增强效用,导致射流孔深度加大;而射流反冲水流的强度降低,对两侧的作用减小,故宽度也相应变窄[16-17],且压力泵为人工调节不易控制,会引起一定的误差。总体来看,数值模拟与实验的射流孔尺寸和形状基本一致,但还存在一定的差异,故需对数值模拟结果进行修正。
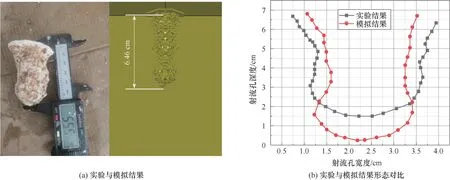
图3 实验与模拟射流孔形态对比Fig.3 Comparison of experimental and simulated jet hole morphology
取表2 中的8 种工况对数值计算结果进行修正。对表2 中数据进行线性拟合,拟合结果见式(1)、式(2)。其中,深度修正相关系数R2=0.974,宽度修正相关系数R2=0.959,修正效果较好。

表2 模拟与实验数据Table 2 Simulation and experimental data
2 响应面实验设计及模型建立
Box-Behnken Design(BBD)是RSM 中较常用的一种实验设计方法,适合多因素交互作用的研究[18-19]。
2.1 实验设计方案与结果
在设计响应面实验前先进行单因素实验,以筛选实验变量,确定各设计变量的变化范围。实验选择实际工程中常用的圆柱形喷嘴,经单因素筛选实验,采用喷嘴出口直径d、射流靶距l和射流压力p作为自变量,分别用X1、X2、X3表示。在稀土矿山开采中,水射流侧向冲蚀开孔的射流孔深度直接影响收液范围,而径宽则影响着射流孔的稳定性,因此以射流孔深度和径宽作为响应值,分别用Y1、Y2表示。通过单因素实验结果,考虑经济以及效率,喷嘴出口直径d控制在0.9~1.5 mm 之间,喷嘴靶距l控制在1 ~5 cm 之间,射流压力p控制在3.2 ~7.2 MPa 之间。因素水平编码见表3。
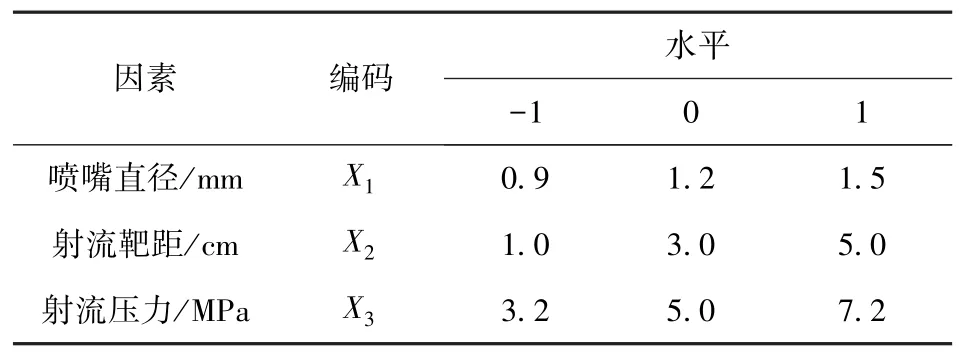
表3 实验因素及水平Table 3 Test factors and levels
根据表3 各因素水平编码值,设计了17 组数值实验(表4),其中数值计算结果深度Y1、径宽Y2已用式(1)和式(2)修正。采用Design-Expert 13 软件对表4 实验结果进行回归拟合分析。
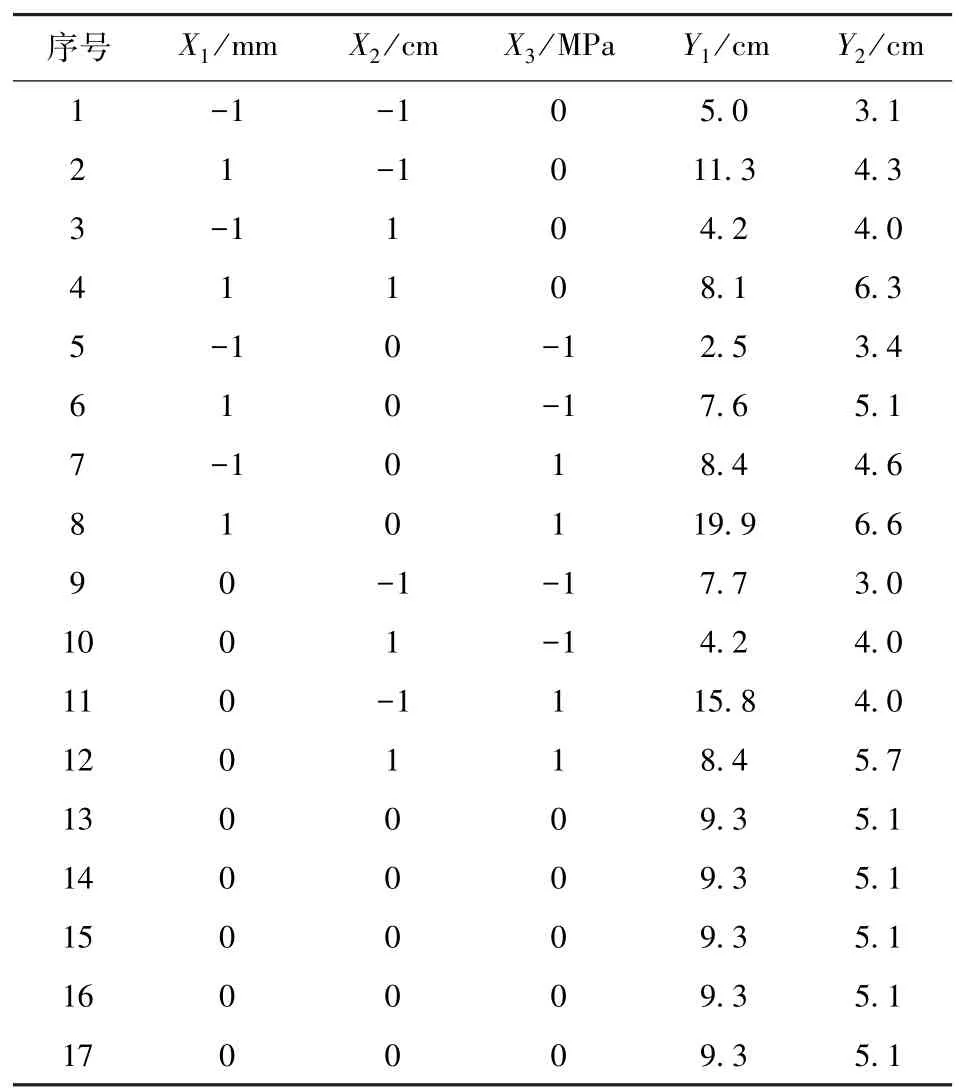
表4 响应面实验设计及结果Table 4 Response surface test design and results
2.2 响应面模型分析
图4 和图5 分别为射流孔深度与径宽的响应曲面及等高线。响应曲面陡、斜率大或等高线接近椭圆,则表示这两个因素之间的交互作用强;若响应面表面平整或等高线接近圆形,则表示交互作用弱。
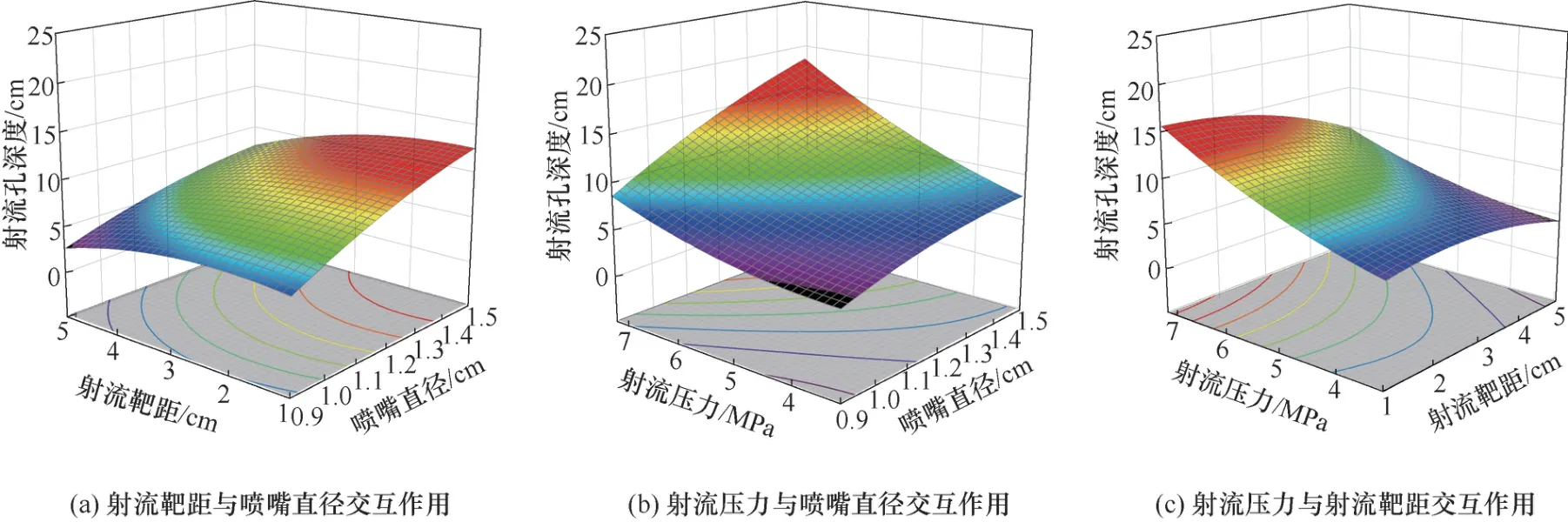
图4 射流孔深度响应曲面及等高线Fig.4 Response surface and contour diagram of jet hole depth

图5 射流孔径宽响应曲面及等高线Fig.5 Response surface and contour diagram of jet aperture width
由图4(a)可知:当射流压力为5 MPa 时,射流孔深度随着喷嘴直径的增大而增大,射流靶距对射流孔深度的影响效果并不明显,响应面的斜率小且等高线偏圆形,表明喷嘴直径和射流靶距之间的交互作用并不显著。由图4(b)可知:当射流靶距为3 cm 时,射流孔随着射流压力的增大而增大,响应面形状不规则,斜率较大且等高线近似椭圆形,表明喷嘴直径和射流压力的交互作用较强。由图4(c)可知:当喷嘴直径为1.2 mm 时,随着射流压力的增加及射流靶距的减小,响应面较平滑曲率较小且等高线接近圆形,说明射流压力和射流靶距对破土深度的交互作用较小。
由图5(a)可知:射流孔径宽随着射流靶距的增大先增大后减小,随着喷嘴直径的增大而增大,响应曲面较陡,等高线呈椭圆形,说明射流靶距和喷嘴直径对射流孔径宽的交互作用较强;由图5(b)可知:射流孔径宽随着喷嘴直径的增大而增大,随着射流压力的增大先增大后趋于平缓,响应曲面较平缓,等高线呈平行线,说明喷嘴直径和射流压力对射流孔径宽的交互作用较弱。由图5(c)可知:响应曲面较陡,等高线呈椭圆形,说明射流靶距和射流压力对射流孔径宽的交互作用较强。
综上分析可以看出,参数间的交互作用对射流孔深度和径宽有着不同程度的影响,有必要在响应面模型中考虑交互项。根据以上3 个参数的一次项、交互项和二次项拟合出的多项式回归方程为
2.3 响应面模型方差分析与检验
表5 和表6 分别为射流孔深度和径宽的响应面模型方差分析结果,模型P值均小于0.05,故射流孔深度和径宽的响应面模型均显著。

表5 射流孔深度模型方差的分析结果Table 5 Analytical results of variance of jet hole depth model

表6 射流孔径宽模型方差的分析结果Table 6 Analytical results of variance of jet hole diameter width model
由F值可以看出,所研究参数对射流孔深度Y1影响顺序为:射流压力X3>喷嘴直径X1>射流靶距X2;对射流孔径宽Y2影响顺序为:喷嘴直径X1>射流靶距X2>射流压力X3。从P值可以看出,因素两两交互作用对射流孔深度影响显著性顺序为:喷嘴直径X1和射流压力X3>射流靶距X2和射流压力X3>喷嘴直径X1和射流靶距X2;对射流孔径宽影响显著性顺序为:喷嘴直径X1和射流靶距X2>射流靶距X2和射流压力X3>喷嘴直径X1和射流压力X3。由于此模型的响应值是通过数值模拟得到的,所以在实验方案中同种工况下得到的响应值一致,故该模型的纯误差为0。
图6 为实际值与预测值对比图,图上的散点整体上接近一条直线,说明预测值接近实际值,该模型具有一定的预测能力。射流孔深度响应面模型相关系数R2=0.944,修正相关系数;射流孔径宽相关系数R2=0.999,修正相关系数,说明模型拟合效果较好。

图6 实际值与预测值对比Fig.6 Comparison of actual and predicted values
3 实验结果分析及优化
3.1 响应面结果分析
图7 为水射流流场分布,整个流场可分为核心区、发散区、卷吸区和回流区。核心区速度分布相对集中,且一定距离内速度不发生改变;发散区随着流动区域不断扩张,速度不断衰减;卷吸区存在于喷嘴两侧附近,随着水射流的不断推进,卷吸作用逐渐降低;回流区存在于土体表面,由于射流能量过大,当接触到土体表面时只有一部分转化为土体内能,其余部分使水沿土体壁面回流形成回流区,回流区水会对土体圆弧壁面产生冲刷作用[20]。

图7 水射流流场分布Fig.7 Water jet flow field distribution
图8 为单因素对射流孔深度和径宽的影响。分析图8 可知:①增大喷嘴直径和射流压力,射流能量也随之增大,射流孔深度自然增大;由于射流能量增大,卷吸区和回流区的能量也随之增大,二者共同作用使射流孔径宽也增大。但相较于喷嘴直径,射流压力的增大在大幅度提高射流孔深度的同时,又避免径宽增长幅度过大。因此,在泵送设备功率允许的条件下,提高射流压力是一种有效途径。②增大射流靶距,由淹没水造成的能量损耗随之增大,射流孔深度随之减小;但射流孔径宽随着射流靶距的增大先增大后减小,因为靶距的增大使射流发散区和射流孔径宽增大。当靶距增大到一定值时,淹没水吸收了水射流的大部分能量,发散区、卷吸区及回流区的流体侵蚀土体能力随之减弱,造成射流孔径宽先增大后减小的现象。因此,若要增大射流深度和减小射流孔径宽,射流靶距应尽量小。
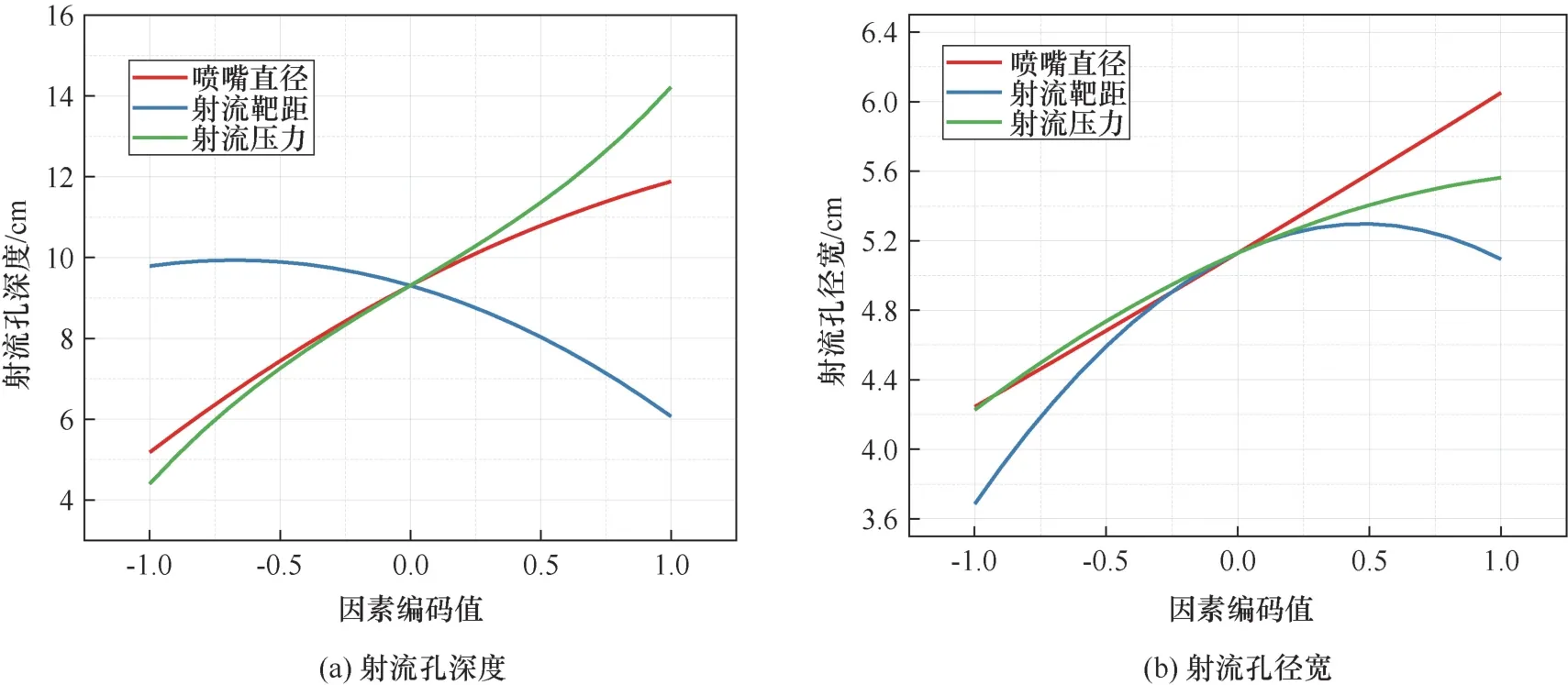
图8 单因素对射流孔的影响Fig.8 Influence of single factor on jet hole
3.2 破土施工参数优化及验证
当考虑多个响应量时,采用单一的响应面函数难以对自变量进行综合求解,故采用基于满意度准则的多目标优化算法对多响应面进行整体优化,记di(yi)(i=1,2,…,I,I为响应量数量)为响应量的满意度,取值范围为0 ~1,数值越大表示满意度越高[21-22]。单响应量满意度函数如下:
式中,yi(x)为第i个响应值;Ui、Li为响应优化区间的上、下限;wi为第i个响应的权重,均取0.5。
式(5)至式(7)分别适用于望大、望小和望目(特定目标值)的响应量。根据不同的优化目的(响应最大值、响应最小值、响应特定值),选择对应的单满意度函数进行计算,对单满意度进行几何加权平均,可得到整体满意度,即
建立目标函数和设计变量之间的关系式后,结合满意度函数对破土施工参数进行多目标优化,优化目标为在3 种不同射流孔深度(Y1=10 cm、15 cm、20 cm)下寻求最优的喷嘴直径(X1)、射流靶距(X2)以及射流压力(X3),同时要求射流孔径宽(Y2)要尽可能的小,因为射流孔径宽越宽,射流孔越不稳定,越容易发生坍塌。破土施工参数优化设计目标见表7。
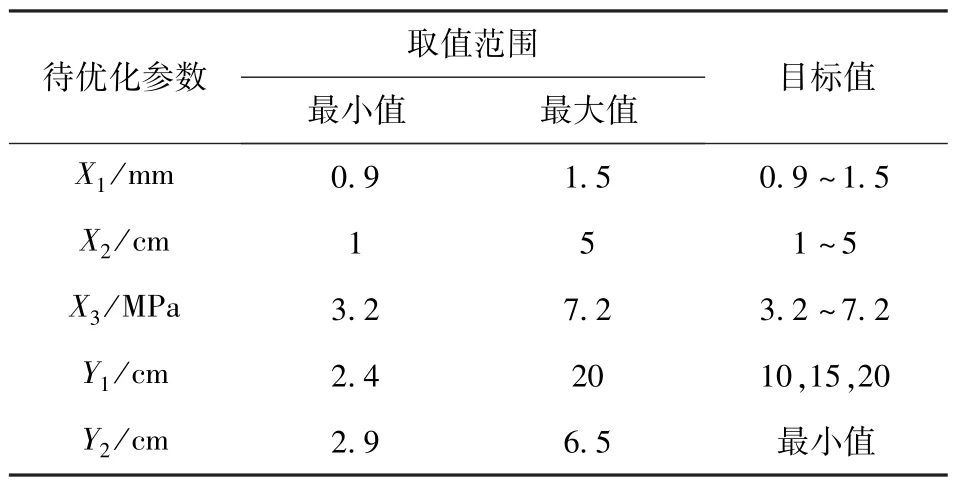
表7 破土施工参数优化设计目标Table 7 Objectives for optimizing design of construction parameters of ground breaking
运用Design expert 13 软件分析求解,响应面优化结果见表8。分析可知,要使射流孔径宽较小,则要较大的射流压力、较小的射流靶距以及控制喷嘴直径。
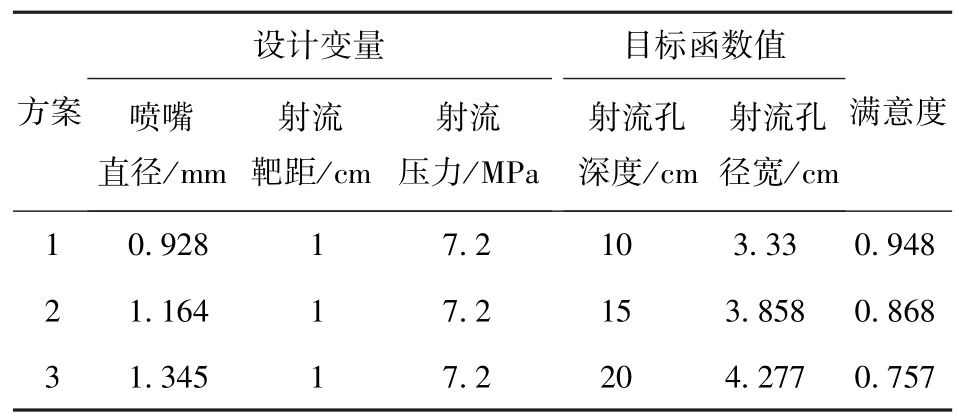
表8 响应面优化设计结果Table 8 Results of response surface optimized design
为了验证优化模型的精确性,对表8 中的3 种方案进行数值模拟验证,模拟结果用式(1)和式(2)修正,优化结果验证列于表9。3 种不同射流孔深度的实验值与预测值的相对误差分别为11.81%、7.87% 和13.99% ,说明射流孔深度的预测模型精度较高。3 种不同射流孔径宽的实验值与预测值的相对误差分别为12.12%、2.28% 和2.06% ,说明射流孔径宽预测模型精度较高。可见,采用响应面-满意度函数法优化,可以提高实验效率,从而获得最佳的破土施工参数。

表9 优化结果验证Table 9 Optimization result verification
4 结 论
(1) 基于ALE 流固耦合算法建立了水射流破土的数值仿真模型,开展室内水射流破土实验对该模型进行验证,仿真与实验结果基本吻合,说明该模型具有一定的准确性。
(2) 通过分析响应面法得到的射流孔深度与径宽方差结果,得到各参数对射流孔深度影响程度依次为:射流压力>喷嘴直径>射流靶距,对射流孔径宽影响程度依次为:喷嘴直径>射流靶距>射流压力;在各因素交互影响中,喷嘴直径和射流压力的交互作用对射流孔深度影响最显著,喷嘴直径和射流靶距的交互作用对射流孔径宽影响最显著。
(3) 采用响应面-满意度函数法对破土施工参数进行优化,并结合数值模拟对该模型进行了验证。当射流孔深度优化目标值分别为10 cm、15 cm 和20 cm 时,模型优化的施工参数(喷嘴直径、射流靶距及射流压力)分别为(0.928 mm、1 cm、7.2 MPa)、(1.164 mm、1 cm、7.2 MPa)与(1.345 mm、1 cm、7.2 MPa);在相应工况下的射流孔径宽均达到最小,即射流孔稳定性强,射流孔深度及径宽预测值与实验值相对误差均小于15% ,说明该优化模型可为破土施工工艺多目标优化提供参考。

