分级加卸载作用下冻结界面黏弹塑性剪切蠕变解耦分析研究

王博通， 张明礼， 王运华， 高 樯， 温 智，周志伟， 马 巍， 王大雁

（1. 兰州理工大学 甘肃省土木工程防灾减灾重点实验室，甘肃 兰州 730050； 2. 新疆驰誉电力工程咨询有限公司，新疆 乌鲁木齐 830002；3. 中国科学院 西北生态环境资源研究院 冻土工程国家重点实验室，甘肃 兰州 730000）

0 引言

我国多年冻土分布面积约占世界多年冻土面积的10%，约占我国国土面积的21.5%，是世界第三冻土大国［1］。随着“西部大开发”和“一带一路”的推进，冻土区公共设施建设不断增加，而这一建设发展的背后也带来了越来越复杂的冻土工程问题。其中，多年冻土活动层经历的周期性冻融过程将导致房屋、路基等结构产生损坏［2］，实际工程中通常采用桩基础来应对这一冻土区工程建设的主要问题。桩基础与冻土界面特殊的冻结作用使得多年冻土区桩基础的承载力得到加强［3］，可将荷载传递至冻土深部，降低基础对外界环境变化的敏感性，可以有效防止活动层冻融循环对基础承载性能的不良影响［3-4］。因此桩基础在多年冻土地区的工程建设中得到了广泛的应用。

研究表明我国青藏铁路有大量桩基础位于高温高含冰量冻土区［5-6］，且冻土区桩基础侧摩阻力的发挥部位多在多年冻土上限下部［3，7］。由于长期的气候作用，该部位广泛分布厚层地下冰［8-9］。桩基工程实践表明冰或者富冰冻土中桩基的变形速率对荷载和温度极为敏感，长期荷载作用下的桩-冰/富冰冻土界面剪切流变特性更为显著［3，6］，因此对于桩-冰/富冰冻土界面的剪切力学特性研究十分必要。何菲等［6］利用自研的大型蠕变剪切仪，进行冻结砂土-混凝土接触界面剪切蠕变试验，获得了高含冰量下桩-土界面的蠕变特征，并提出考虑含冰量影响的界面剪切蠕变模型。Morgenstern 等［10］结合工程实践，基于多晶冰中稳定蠕变阶段的公式［11］对冰和富冰冻土中桩基础蠕变变形进行了推导并提出了预测模型，但该模型参数较多，且对于少冰和富冰冻土的界限规划不清。以上研究对于冰或富冰冻土中桩基础冻结界面剪切蠕变变形特征仍有不足，关于桩-冰或富冰冻土界面的剪切蠕变试验还需继续开展。

现有研究通常采用直剪试验及压柱试验［3，6，12-13］来探究多年冻土中桩基础冻结界面的剪切力学特性。何鹏飞等［14］通过冻土-混凝土冻结界面进行直剪试验，研究了冻土-混凝土界面冻结强度特征与形成机理；魏国帅［15］对细砂-混凝土进行低温直剪试验，探究了温度、接触面冰膜厚度、法向应力对于桩周土冰膜流变特性的影响；石泉彬等［16］通过压柱法研究瞬时荷载作用下冻土与结构接触面冻结强度的影响规律。已有常规的低温剪切试验大多在大型低温冷库中进行，控温精度差且剪切试验加载方式单一，未考虑到桥梁、粮仓、储油罐等的间歇受荷作用，不能对长期荷载作用下的冻结界面的剪切蠕变变形进行解耦分析。

本文在压柱试验的基础上，通过将高精度控温箱与材料试验机组合，进行了钢管-冰冻结界面加卸载剪切蠕变试验。试验系统不仅实现了对试样的精准控温，还通过材料试验机实现复杂的加卸载方案。通过对加卸载作用下钢管顶部变形的分段独立解耦，获得钢管-冰冻结界面剪切蠕变变形过程中黏弹塑性变形的具体量值及其在长期蠕变变形中的贡献，探究了冰-钢管界面的剪切变形特征及机制，为冰和富冰冻土中桩基础长期变形的研究提供理论参考。

1 分级加卸载试验

1.1 试验装置

本试验在具有可控温恒温箱的材料试验机中进行，利用高精度恒温箱对试样进行单独控温，同时利用材料试验机进行加载，可实现多界面的良好恒温效果及加载程序精确控制。试验采用的冰-钢管结构如图1 所示。通过对钢管顶端的竖向加载，实现冰-钢管界面的剪切受力。界面的相对剪切变形和剪切应力分别通过钢管顶部的位移，钢管顶部荷载及钢管侧面积换算获得。制备冰-钢管结构的制样模具由环形钢圈和可拆卸的中心带孔底板组成。底板上预先设置限位装置可以保证环形钢圈的中心与底板孔中心对齐。环形钢圈直径为24 cm，高度28 cm。钢管壁厚3 mm，直径5 cm，高30 cm。底板的圆孔直径（6 cm）稍大于钢管直径，以保证钢管底部不受力，冰-钢管界面承担全部压头作用力。底板下方安装高2 cm 的垫片，来确保钢管在压头作用力下产生足够竖向位移，但钢管底端始终不受力。由于试验过程中接触面压应力沿钢管分布并不均匀［16］，计算分析过程中采用平均剪应力代替冰-钢管界面上的剪应力。

1.2 试样制备

本实验采用Q235钢管模拟桩体。冰-钢管结构的制作过程如图2所示，试样制备时，将钢桶和钢管置于平底塑料盆中，利用直尺测量钢管与环形钢桶的相对距离，保证钢管与环形钢圈的相对位置居中，并采用水准仪矫正垂直，再利用胶带进行固定，保证在结构转移过程中相对位置不变。将调整好的试样放置于温度为-25 ℃的控温冰箱内，并再次进行水准仪垂直检查。检查完成后开始加水冻结。为避免管周水冻结过程中产生的明显冻胀改变钢管的相对位置，试样中冰的制作采用分层加水冻结法［3］。加水时控制每次加水高度不超过3 cm，每次冻结时间不小于4 h。由于冰的不透水性，第二次加水后水分不会从钢桶中外渗。冻结完成后，为防止冰在恒温过程中升华，在试样上下端采用塑料薄膜进行包裹。

图2 冰-钢管结构制作过程及钢桶内的分层冻结冰样Fig. 2 The production process of ice-steel tube structure and the layered frozen ice sample in the steel bucket：vertical correction of steel tube （a）， steel tube center correction （b）， layered frozen ice （c）

1.3 加载方案

试验采用力控制方式进行分级加卸载，加卸载速率为100 N·s-1。加载方式见图3。初始加载值设置为5 kN，荷载增幅为2 kN。加卸载速率设置为100 N·s-1。设置饱载时间为4 h，空载时间为2.5 h。其中空载设置时设置稳定荷载为20 N，保证压头和钢管顶保持接触，便于测量钢管顶部位移。具体试验操作如下：钢圈中的冰-钢管结构冻结完成之后，用塑料薄膜包裹，根据底板的卡槽位置将带有钢圈的冰-钢管结构居中安装在图1 中所示的空心底板上。然后将冰-钢管结构及底板整体放置在具有可控温恒温箱的材料试验机中。设置恒温箱温度为所需的试验温度，恒温24 h 以上。调试好加压装置，然后在材料试验机的控制系统中按预先的加载方案设置加载程序。温度恒定之后按照预设加载程序进行加载，并用材料试验机的数据采集系统收集试验过程中钢管顶端的荷载和位移数据。分别进行试验温度为-3 ℃、-5 ℃的冻结界面加卸载蠕变试验。

图3 加卸载蠕变试验加载方式Fig. 3 Loading and unloading creep test loading method

2 结果与分析

2.1 变形解耦分析

图4是-3 ℃环境中首级加卸载作用下冻结界面相对剪切变形曲线。可以看出，在对钢管施加首级荷载后，钢管顶部产生瞬时竖向位移（a—b 段）。压头作用力增加至首级荷载并保持稳定后，钢管顶部产生蠕变变形（b—c段）。钢管顶部依次出现卸载瞬时弹性回弹（c—d 段），以及与时间有关的黏弹性恢复（d—e 段）。由于钢管的模量远高于冰，对钢管顶部施加荷载后假设钢管不发生压缩变形，钢管顶部的变形与冻结界面的剪切相对变形相等。S为加载过程中的钢管顶部变形值。Sp为卸载后的不可逆残余变形，即剪切作用下冰-钢管界面的相对塑性变形，Si为瞬时变形，Sv为蠕变变形［17］。从图中可以看出，冰-钢管界面的总剪切变形可分为四部分，即：瞬弹性变形Sie；瞬塑性变形Sip；黏弹性变形Sve；黏塑性变形Svp。各分段变形间的量值关系见式（1）。

图4 -3 ℃首级加卸载作用下变形曲线Fig. 4 Deformation curve under the first stage loading and unloading at -3 ℃

由式（1）可知，图4中加载过程中的瞬时变形阶段a—b 可由卸载过程中的可逆瞬时弹性恢复阶段c—d 对其进行解耦，饱载过程中的蠕变变形阶段b—c 可由空载过程中的可逆黏弹性恢复阶段d—e进行解耦。由试验结果可知，加载至首级荷载5 kN时对应的瞬时变形值Si为1.398 mm，对应瞬时弹性恢复变形值Sie为0.401 mm，由此解耦分析得出对应的瞬塑性值Sip为0.997 mm。饱载4 小时对应的蠕变变形值Sv为0.070 mm，空载过程中的可逆黏弹性恢复值Sve为0.010 mm。由图5（b）可知，2.5 h 后黏弹性恢复速率衰减至0，黏弹性变形不再发生，此后的蠕变变形即为黏塑性变形。进行解耦分析可知Svp为0.060 mm。

图5 -3 ℃钢管-冰结构分级加卸载下广义应变及其速率时程曲线Fig. 5 Generalized strain and its rate time history curve of steel tube-ice structure under graded loading and unloading at -3 °C： generalized strain time history curve （a），generalized strain rate time history curve （b）

2.2 变形时程曲线特征

图5 为-3 ℃环境中冰-钢管界面在加卸载作用下的广义应变及其速率时程曲线。其中，广义应变γ͂及其速率̇的计算如下：

式中：ΔL表示某时刻下桩-冰冻结界面的剪切变形值；L表示桩-冰冻结界面的接触长度；t表示该应变对应的时间。

由图5 可知，饱载时的蠕变阶段对应的广义应变速率在加载前期速率增加规律不明显，第三级荷载之后呈现明显的增加规律。在卸载的瞬间冰-钢管界面产生快速的瞬时可逆恢复变形，其量值随应力水平的提高而加大，这与灰质黏土的规律一致［17］。而在空载时的可逆黏弹性恢复阶段，各分级剪应力对应的广义应变速率均呈现出衰减趋势。结合表1 中数据及图5（b）可知，卸载后2.5 h 内，黏弹性恢复速率逐渐趋于0，黏弹性变形值在蠕变变形中总体占比较小，-3 ℃下占比集中于12%～30%。空载阶段之后保留的残余塑性变形随加卸载的逐级进行，其变形值逐渐增大。

表1 -3 ℃分级加卸载作用下各阶段变形及速率值Table 1 The deformation and rate values of each stage under the action of graded loading and unloading at -3 ℃

在图5中，分级应力小于250 kPa时，饱载下的蠕变变形速率未出现明显升高趋势，变形呈衰减特征并最后保持稳定速率持续变形。这是由于冰的成分和微观结构的差异，导致其蠕变特征较常规岩土材料更为明显［3］。试验持续时间尺度内（小时），岩土体材料蠕变速率在较小应力水平下呈现衰减蠕变特征，且蠕变快速衰减至0，不易发生持续的稳态蠕变。而冰是一种明显的黏塑性材料，冰-钢管界面在承受剪应力时极易产生流动［18］。在较小荷载水平下会以大于0 的速率产生蠕变变形，且随着分级荷载的增加，蠕变速率逐渐变大，其原因是结构中较高的剪应力水平将导致冰的流动速度加快以及结构缺陷的发展［19］。当冰-钢管界面剪切应力达到296 kPa 时，对应的蠕变速率不再稳定，呈现加速蠕变趋势，此时冰-钢管界面已出现破坏，这与土体的蠕变试验结果相似［17］。当分级剪切应力增加到341 kPa并饱载时，界面剪切变形迅速发展并超过4 mm，冻结界面的承载能力丧失。相关研究［20-21］表明施加的分级剪应力大于界面的长期强度极限τ0时，冰-钢管界面的蠕变速率在荷载作用下，随着微裂纹的萌生和扩展先衰减并保持短暂稳定，直至裂纹合并引起加速蠕变。且在较大界面剪切力作用下，管周冰发生冰颗粒的融化并破裂［22］，导致冰-钢管界面力学特性被弱化，冻结界面产生显著变形，结构发生明显的塑性破坏。

图6为分级剪应力下黏弹塑性变形中瞬塑性变形、黏弹性变形、黏塑性变形分量及黏性变形平均速率。各级剪切应力下的黏性变形平均速率Ṡv计算如下：

图6 -3 ℃分级剪应力对应各阶段变形值及黏性变形速率Fig. 6 The graded shear stress at -3 ℃ corresponds to the deformation value and viscous deformation rate of each stage：the instantaneous plastic deformation value under each graded shear stress （a）， viscoplastic deformation value under each graded shear stress （b）， viscoelastic deformation value under each graded shear stress （c），the average creep rate under each graded shear stress （d）

式中：为第n分级下的黏性变形；t(n)为第n分级下的饱载时间，此处取4 h。

图6（a）、（b）是各分级剪应力下瞬塑性变形、黏塑性变形分量。从中可以看出，在初级加载作用下，瞬塑性变形从0.997 mm 迅速下降到0.002 mm，而后一直在0附近。瞬塑性影响逐渐消失。黏塑性变形在加卸载作用的前期变化不明显，除首级荷载外，其变形值均为瞬塑性变形值的8～52 倍，远大于瞬塑性变形值。

2.3 变形指标变化规律

2.3.1 广义剪切模量变化特征

图7 是-3 ℃、-5 ℃下各级荷载下广义剪切模量及其变化幅值。其中广义剪切模量͂的计算如下：

图7 -3 ℃、-5 ℃广义剪切模量值（a）及增加幅度（b）随荷载水平变化规律Fig. 7 The variation law of generalized shear modulus value （a） and increase amplitude （b） at -3 ℃ and -5 ℃ with load level

式中：F(n)为第n分级荷载；H为冰-钢管界面高度；D为钢管横截面周长。本文中的剪切模量计算方式与以往学者［6，19］有所不同，即通过加卸载作用下解耦分析，在瞬时加载对应的变形中剔除了瞬塑性变形，只保留弹性变形。

可以看出，剪切模量随荷载的增加逐渐增大，模量增加幅度呈减小趋势。表明在冻结界面分级加卸载剪切蠕变过程中，界面及其接触带出现了明显的强化效应。这主要是加载前期应力作用下冰-钢管界面附近冰晶间滑移和压密作用所致［2］。结合图6（a）可以看出，-3 ℃加载前期瞬塑性变形为0.997 mm，此后变形值介于0.001～0.031 mm，远小于首级荷载作用下的瞬塑性变形值。即加载后期压密作用对于界面强化的贡献开始减弱，但界面的广义剪切模量依然小幅增加。结合其他学者的研究［3，22］，加载后期界面的强化主要是由于冰晶在加载阶段滑移和破裂后，空载阶段的重结晶作用所致。

2.3.2 黏弹性变形分析

为对比各分级荷载下的黏弹塑性变形，将各个不同时间段的黏弹性变形归零处理，在时间区间0～2.5 h 内进行对比分析。图8 为-3 ℃、-5 ℃下，将各分级剪应力下的黏弹性恢复阶段时间归零的时程曲线。从图8（c）、（d）中可以看出，黏弹性变形总体随着饱载时间的进行呈现衰减趋势，变形速率在卸载后2.5 h 内快速衰减至0，卸载后界面黏弹性变形恢复基本完成。随着分级剪应力的增大，黏弹性变形值亦增加。2.5 h 内，-3 ℃各分级剪应力所对应的黏弹性变形占饱载下蠕变变形的比例依次是14%、30%、27%、12%；-5 ℃各分级剪应力所对应的黏弹性变形占饱载下蠕变变形的比例依次是7%、25%、32%。

图8 -3 ℃、-5 ℃黏弹性变形及其速率时程曲线Fig. 8 Viscoelastic deformation at -3 ℃ and -5 ℃ and its rate time history curve： viscoelastic deformation at -3 ℃ （a），viscoelastic deformation at -5 ℃ （b）， viscoelastic deformation rate at -3 ℃ （c）， viscoelastic deformation rate at -5 ℃ （d）

2.3.3 塑性变形分析

图9 为-3 ℃和-5 ℃条件下，将各分级剪应力下的黏塑性变形阶段时间归零的时程曲线。从图9（a）中可以看出-3 ℃下，在剪应力为114 kPa时，对应的黏塑性发展速率逐渐减小，塑性变形呈现衰减趋势。随着剪应力的逐步加大，其变化速率逐渐增大，塑性变形过程逐步趋于加速变形。这是由于在加载初期，冰-钢管界面没有被完全压实，在很小的荷载作用下其黏塑性变形较大。随着饱载时间的不断增加，由于冰的剪切流变性与剪应力水平显著相关，界面产生塑性流变［19］。而-3 ℃下随着剪应力达到296 kPa，冰-钢管界面出现损伤，黏塑性发展呈现出加速变形的趋势。-5 ℃下，由于界面冻结力较高，试验加载并未破坏，从图9（d）可以看出-5 ℃下冰-钢管界面黏塑性发展都呈现衰减趋势。

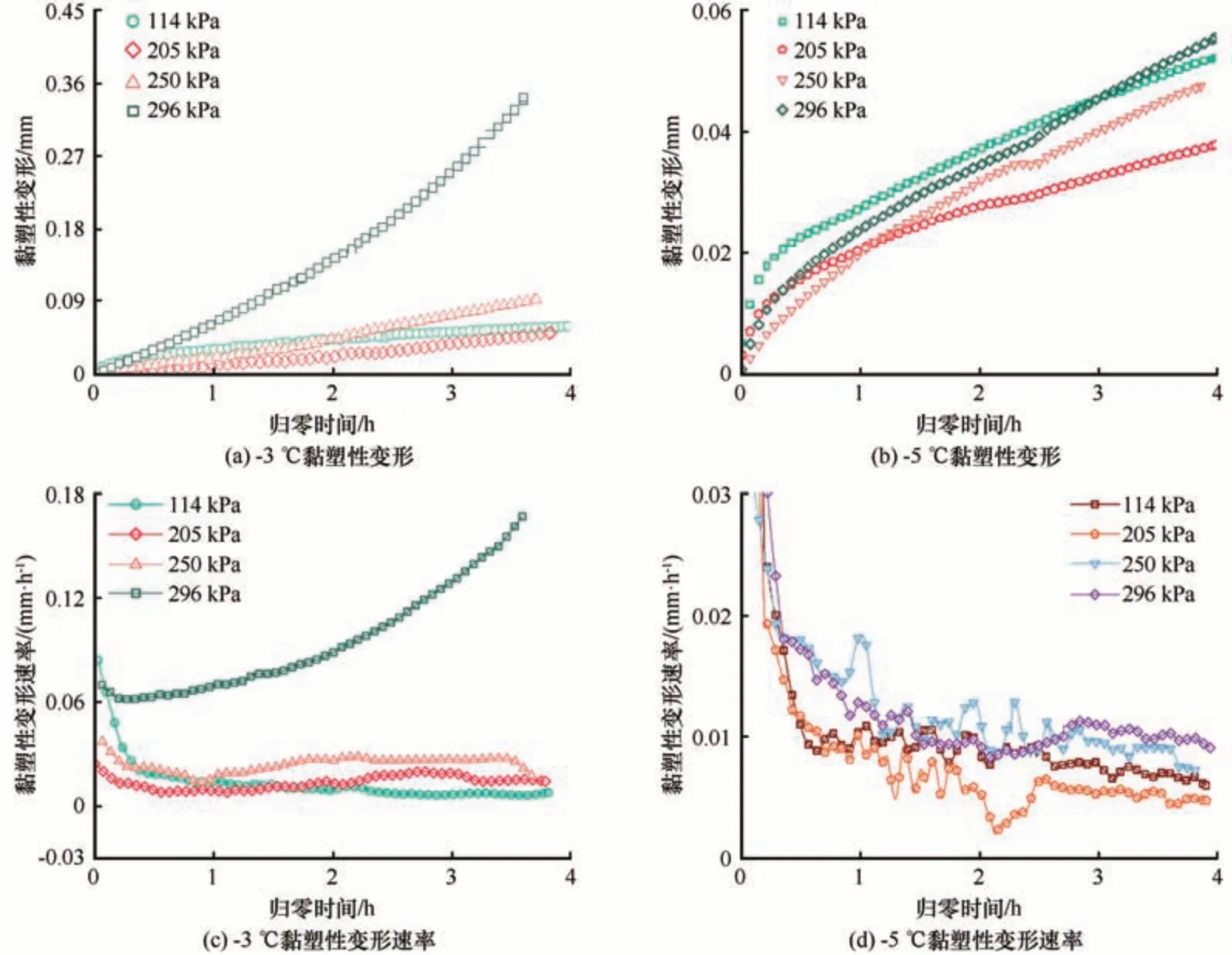
图9 黏塑性变形及变形速率时程曲线Fig. 9 Viscoplastic deformation and deformation rate time history curve： viscoplastic deformation at -3 ℃ （a）， viscoplastic deformation at -5 ℃ （b）， viscoplastic deformation rate at -3 ℃ （c）， viscoplastic deformation rate at -5 ℃ （d）

图10 为-3 ℃、-5 ℃环境中塑性变形Sp在各分级荷载下累计变形S中的占比。结合图5 可以看出，在界面破坏前，-3 ℃饱载时蠕变呈衰减趋势，-3 ℃下当界面剪应力达到296 kPa 进行饱载时，钢管-冰界面蠕变变形进入加速蠕变，界面出现破坏，此时塑性变形在总变形中的占比出现陡增，占比达到71%。剪应力为159 kPa 时，塑性变形在总变形中的占比最低，为69%。由于-5 ℃下界面未被破坏，塑性变形占比总体呈现出减小趋势。

结合图6（a）、（b）的变化关系可以看出，塑性变形在前期由瞬塑性变形主导。随着分级加卸载过程的不断进行，由于冰-钢管界面被压实［2］，瞬塑性变形逐渐消除。而黏塑性发展不仅与时间有关，还与荷载的大小有关系［22］。随着分级加卸载的不断进行，塑性变形主要由黏塑性主导。由此可以考虑在实际工程施工上部结构时，可先给桩基础施加预荷载并饱载一段时间，不仅可以消除瞬塑性变形的影响，同时可以增强桩-冰/富冰冻土间剪切刚度，从而提升桩基础的承载性能。

3 结论

（1）通过对分级加卸载作用下冻结界面蠕变变形过程的分段独立解耦，发现冻结界面剪切蠕变变形主要由瞬弹性、瞬塑性、黏塑性变形组成，且存在黏弹性变形。在2.5 h 内，黏弹性变形恢复速率基本趋于0，且-3 ℃下黏弹性变形值在蠕变变形中占比较小，总体小于49%，集中于12%～30%，-5 ℃下黏弹性变形值在蠕变变形中占比小于35%。

（2）冻结界面剪切模量随界面剪应力水平的增加逐渐增大，瞬塑性变形随荷载的增加迅速减弱，蠕变过程中结构未破坏以前界面存在明显的强化效应。

（3）冻结界面剪切蠕变特征随荷载级别的增加由衰减向非衰减过渡。即黏弹性变形和低剪应力水平下黏塑性变形表现为衰减性蠕变，而高应力水平下黏塑性表现为非衰减性蠕变，且变形速率随剪应力水平增加显著提升。

（4）分级加卸载作用下，冻结界面塑性变形在总变形的占比中存在一个最小比例。在冻土区构筑物建设中，可在上部结构施工时先施加预应力以消除瞬塑性变形，提高冻结界面剪切模量，强化富冰冻土及厚层地下冰中桩基础的承载性能。