单轴循环荷载下冻结土石混合体动弹性模量和累积塑性应变研究
孙 凯, 李志清, 孔佑兴, 周应新, 王双娇
(1. 中国科学院 地质与地球物理研究所 页岩气与地质工程重点实验室,北京 100029; 2. 中国科学院大学,北京 100049;3. 中国科学院 地球科学研究院,北京 100029; 4. 云南省交通投资建设集团有限公司,云南 昆明 650100)
0 引言
青藏高原地处高寒高海拔地区,冻土发育,地震活动频繁,我国川藏铁路、中尼铁路等工程建设面临严峻的挑战[1]。高原地区的冻土往往不是单一性质的土体,而是含有块石组成的复杂岩土体,这种岩土体也广泛应用于路基填筑、土石坝等人造工程中。在地震、车辆荷载等循环荷载作用下,寒区土石混合体构筑物(如路基和边坡)的抗震性和稳定性逐渐成为研究的重点[2-5]。因此,研究动荷载条件下冻结土石混合体力学特性具有重要的理论价值与工程意义。
相较于冻土的研究,冻土石混合体动力学研究成果较少。土石混合体的力学特性受多种因素影响,包含有含石量、块石形状、基质组分、矿物成分、粗糙度等因子[6-7],其复杂的力学特性与冻土存在差异,崔凯等[8]在研究地震荷载作用下混合土动力学特性时,采用Hardin-Drenvich 模型来拟合试验数据,计算了动剪切模量和泊松比,分析得到随着围压的增大动剪切模量和泊松比增大。凌冲颖[9]开展了冻结粗粒土长期循环作用下的力学特性研究,探究了冻结粗粒土疲劳损伤特性及强度特性。Zhang等[10]在单一温度下开展了动三轴试验,探究了不同粗粒含量下,冻结土石混合体的动剪切模量和滞回环变化特征。但文中仅在一个温度条件下开展实验,缺乏说服力。Payan 等[11]通过将几种粒度分布的砂与不同比例的二氧化硅非塑性粉土混合,研究了混合物的小应变动力特性,讨论了非塑性细粉含量对动弹性模量和阻尼比的影响。可见,少有学者研究在不同温度条件下,冻结土石混合体的动弹性模量和动应力-应变的变化规律。
厘清岩土体累积塑性应变规律,探究其演化模型是解决循环荷载作用下路基动力稳定性和沉降问题的关键。关于循环荷载对岩土体累积塑性应变的演变模型,学者多采用经验拟合的方法。目前已建立以Monismith 模型为主的经验模型,并且因其简洁实用,而被广泛应用。针对冻结岩土体,张斌龙等[12]通过动三轴试验,研究冻结黏土的轴向累积塑性变化规律,建立了冻结黏土塑性安定和塑性蠕变临界动应力表达式。Zhang 等[10]在开展低温循环试验的基础上,提出了修正后的Monismith 累积塑性应变方程,能够更好地拟合试验结果,但文中未对模型参数进行探究,试验结果也仅在-6 ℃条件下开展,合理性有待探讨。累积塑性应变模型受多种工况影响[13],目前大部分研究已建立了相应的模型,但仍存在试验条件少,试验条件与模型参数相关性差的问题。
为了更进一步了解寒区冻结土石混合体的动力学特性,本文以循环荷载下冻结土石混合体的应力-应变机制为切入点,以累积塑性应变和动弹性模量为动力学指标,研究冻结土石混合体在不同条件下的动应力-应变关系、滞回环特征、动弹性模量变化规律,并给出了循环荷载作用下累积塑性应变模型。
1 材料与方法
1.1 材料与样品制备
试验采用重塑试样,基质土为粉土,最大干密度为1.5 g·cm-3,土体的塑限和液限分别为17.8%和32.1%。采用的块石颗粒为石英颗粒,其颗粒尺寸介于6~9 mm 之间、天然密度为2.67 g·cm-3,点荷载强度为10.2 MPa。土颗粒及块石粒径级配曲线和样品照片如图1(a)所示。

图1 土石粒径Fig. 1 Soil and rock grain size: block photograph (a), block grain size diagram (b)
试样制备过程如下:取烘干后过2 mm 筛的土样,加入一定量的蒸馏水,静置24 h,配制成25%含水量的土样。将土样和块石混合并搅拌均匀,放入直径50 mm,高100 mm 的圆柱形模具中,分三层进行压实,配置成含石量为30%、40%、50%的土石混合体试样。将未脱模的试样连同模具包裹好保鲜膜后,放入-30 ℃条件的试验箱中,低温保存24 h以上,而后在-5 ℃、-10 ℃、和-15 ℃条件下保存24 h,进行试验。根据Medley[14]提出的土石阈值为0.05LC[LC为工程特征尺寸,此处取圆柱体试样的直径(50 mm)],可得到本次试验的土石阈值为2.5 mm,故试验选用过2 mm 筛的粉土作为基质土。通过试验研究表明块石最大尺寸介于试样直径的1/6~1/4,可基本消除尺寸效应的影响[15],因而采用6~10 mm的块石颗粒。
1.2 试验方法
本文采用KTL-DYN10动三轴试验仪,进行低温单轴循环荷载试验,仪器的最大轴向荷载为10 kN,轴向力分辨率为5 N(轴向传感器位于压力室内部),允许最大围压为2 MPa,轴向加载频率范围为0~5 Hz,加载波形包括正弦波和方形波。
为保证试样在实验过程处于恒温条件,在试验过程中对试样进行保温处理,保温方法简易图如图2(a)所示。具体过程如下,试样从恒温箱中取出后,先包裹保鲜膜(减少与空气进行水分交换)再用一层隔热棉包裹(防止热辐射和热传导),而后在外层包裹冰袋(避免试样与外界接触,防止与空气进行热传导),放入试样底座上。试样处于封闭的环境,基本无空气流动,从而降低因对流而散失热量。该保温措施参考Li 等[16]研究低温土石混合体单轴压缩条件下破坏模式的保温方法,并对保温措施进行了改进。同时通过试验测试样表面温度变化规律,发现在25 min 内完成试验,样品表面温度变化约为1.4 ℃,该条件满足实际实验要求。

图2 试样加载及保温示意图Fig. 2 diagram of specimen loading and maintaining temperature: thermal insulation (a), loading (b)
本文在不同含石量(30%、40%、50%)、不同温度(-5 ℃、-10 ℃、-15 ℃)、不同幅值(1.5 MPa、2.0 MPa、2.5 MPa)条件下开展了正弦振动荷载单轴压缩试验,加载曲线如图2(b)所示。Rollins 等[17]采用频率为0.01~2.00 Hz 进行的砾石土循环加载测试试验,Aghaei 等[18]采用0.01~1.00 Hz 的堆石材料下使用稳态正弦循环进行的动力学试验。国内惯用的粗堆石料振动力学试验加载频率为1 Hz[10-19],王庆志等[20]在研究冻土区青藏铁路路基的动力学特性时指出,青藏铁路在多年冻土区的平均运营时速是120 km·h-1,对应车载动荷载频率为1.3 Hz,综上所述,本研究结合前人基础上选取加载频率为1 Hz。
按照张献才[21]研究指出等幅循环振动试验中幅值应力取单轴下峰值应力的0.5~0.9 倍,每组方案分别取三组不同的幅值,本实验将采用0.83σmax、0.67σmax、0.50σmax。为对比不同含石量和温度下,土石混合体在相同幅值应力条件下的动力学特性,σmax取温度为-5 ℃、含石量40%单轴状态下的峰值应力(通过试验得到σmax= 3 MPa)。徐学燕等[22]指出下限应力在0.003~1.525 MPa 间改变时,对冻结试样变形影响小。本试验选取0.3 MPa为循环的下限应力,即轴向荷载为0.6 kN。综上,根据实际试验条件和最大轴向应力,选取的三组轴向幅值为1.5 MPa、2.0 MPa 和2.5 MPa,循环的下限应力为0.3 MPa。具体工况条件见表1。

表1 试验工况Table 1 The test conditions
1.3 振动荷载物理参数
动弹性模量和累积塑性应变为评价岩土材料动力学性能的关键参数[23]。结合规范及实际试验数据,动弹性模量是相邻循环加载-卸载围成封闭曲线的割线斜率(图3),并按照式(1)计算得到。累积塑性应变是指在加载—卸载的往复循环过程中不断产生的塑性应变。循环加载过程中由于塑性应变持续累积,相应的动力学性能(例如动弹性模量)也会产生变化,因此在达到不同应变后,动弹性模量可以认为在相应累积塑性应变下试样的动弹性模量。

图3 循环加载试验理论曲线Fig. 3 Theoretical curve of cyclic loading test
动弹性模量按照下式计算:
式中:σd,max为滞回环上的最大应力;σd,max为滞回环上的最小应力;εd,max为滞回环上最大应力对应的应变;εd,min为滞回环上的最小应力对应的应变。本次试验的终止条件是轴向累积塑性应变达到20%或循环次数达到3 000次。
2 结果与分析
2.1 动应力-应变特征
土体的动应力-应变关系是表征土体动力学特性的关键,也是分析土体动力破坏的重要基础。图4 为不同温度条件下的动应力-应变曲线试验结果,可见轴向应力在每个周期内波动变化。在达到第一次循环的幅值前,应力-应变曲线有明显的应变强化阶段。另外,图4中应力-应变曲线组成的滞回环相对位置呈现出稀疏—密集—稀疏的规律,图4(b)尤为明显(为了清晰地展示试验结果,笔者在横轴上设置了断点隐去了部分应力-应变曲线)。以图4(b)为例,初始8次循环加载,可逆塑性应变逐渐增大(即累积塑性应变逐渐增大),滞回环的相对位置表现出稀疏的特征,这主要是单个循环后产生的应变逐渐增大;而后随着循环次数的增大,应变达到7%左右时,单个循环对应的不可逆塑性形变量逐渐变小,即动应力-应变曲线的滞回环相对位置表现出密集的规律;最后,当应变达到14%时,滞回环的相对位置又表现出稀疏的特征。在循环荷载作用下,前后滞回环的相对位置不重合,表明冻结土石混合体具有明显的应变累积性。

图4 40%含石量条件下不同幅值应力的动应力-应变试验结果Fig. 4 Dynamic stress-strain test results for different amplitude stresses under 40% rock content conditions:15 ℃ (a), -10 ℃ (b), -15 ℃ (c)
发生上述现象的可能原因如下:初期循环荷载作用下试样内部存在颗粒压密和微裂纹闭合,导致单个循环荷载下对应的塑性应变大,滞回环相对位置表现出稀疏的特征;随着微裂纹闭合,试样抵抗循环荷载的能力增强,单个循环对应的应变减小,滞回环相对位置表现出密集的性质;随着应变的继续增大,试样中裂纹开始发育和贯通,单个循环对应的应变增大,滞回环相对位置表现出稀疏的性质。
为了进一步明确滞回环的变化特征,以-10 ℃、幅值应力为1.5 MPa 下含石量40%的土石混合体试验结果为例,进一步讨论滞回环分阶段的变化规律。图5(a)~(d)给出了滞回环的演化规律,其中横坐标的长度均为1%(应变)。总结发现以下结论:①单个滞回环初期阶段循环的面积最大,但是随着循环加载次数的增加,滞回环面积先逐渐变小后逐渐增大。此外,在初始阶段,加载-卸载曲线重合度小,随着应变的增大,加载-卸载曲线逐渐重合[见图5(b)中黑色和红色滞回环逐渐重合]。而后,随着当循环次数达到183 次时(以40%含石量,温度-10 ℃为例),相邻滞回环又逐渐分离[图5(c)和图5(d)]。②动应力-应变曲线呈现出非线性特征,滞回环初期为不闭合的椭圆形[如图5(a)所示],循环次数增大,滞回环逐渐变化为柳叶形[图5(b)],动应变继续增大(循环加载次数到达1 676 时),最后滞回环呈现出近似闭合的扁长椭圆形[图5(c)和图5(d)]。③图5(a)~(d)中单个滞回环起点到终点的距离,有先减小后增大的趋势,可见,随着加载循环的增加,不可逆累积塑性应变逐渐增加。
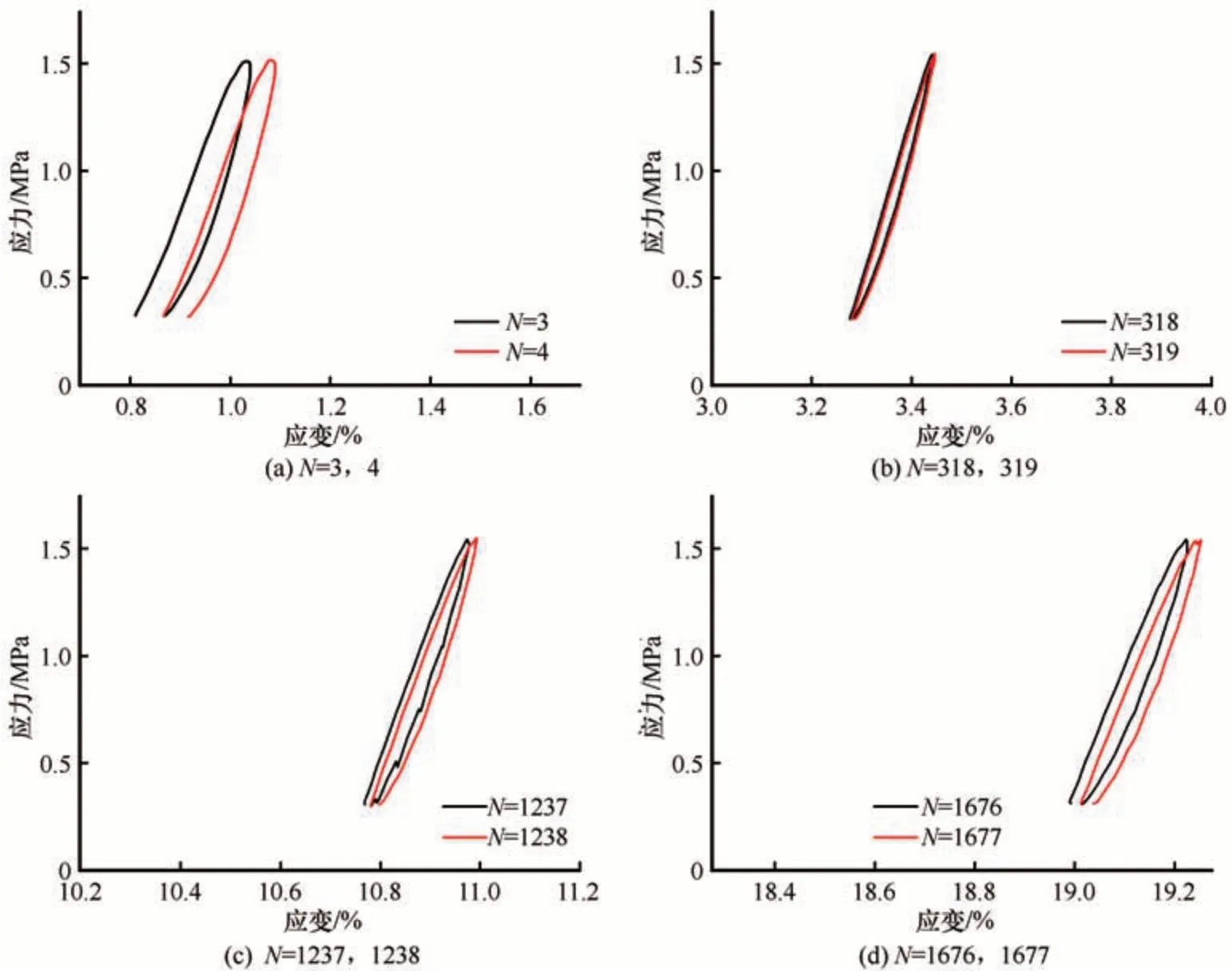
图5 不同循环次数下相邻循环处的应力-应变曲线Fig. 5 Stress-strain curves at adjacent cycles for different number of cycles: N=3, 4(a);N=318, 319(b); N=1 237, 1 238(c); N=1 676, 1 677(d)
2.2 动弹性模量的变化规律
动弹性模量作为评价岩土体动力学特性的关键指标,动弹性模量越大,试样抵抗振动荷载破坏的能力越强,反之抵抗循环荷载破坏的能力弱。动弹性模量的影响因素包括材料本身特性和含水量等[23]。而在低温土石混合体中,温度是影响土石混合体特性关键因素[24]。本文通过循环单轴试验取得了试样动应力-应变关系,按照式(1)计算得到每次循环条件下的动弹性模量。
图6为不同温度和含石量条件下试样累积塑性应变与动弹性模量之间的关系,其中每个数据点代表每个循环次数所对应的动弹性模量,可见动弹性模量存在明显的波动性。其波动性可能是由于试样中块石咬合导致应力集中所致,从而在宏观上表现出弹性模量的波动性。另外,初始变形阶段弹性模量存在明显的增大趋势,这与前一节提到累积塑性应变的稀疏阶段类似,其原因可能是冰土组成的胶结物与块石之间的裂缝逐渐闭合,并且试样进一步压实,块石和土体的咬合和嵌固作用更为明显。微裂纹的闭合和块石的嵌固作用增强,能够在一定程度上提高试样的动弹性模量。

图6 三种含石量条件下不同温度动弹性模量与累积塑性应变的变化情况Fig. 6 Variation of dynamic elastic behavior modulus and cumulative plastic strain at different temperatures for three rock content conditions: 30% (a), 40% (b), 50% (c)
通过图6可见,相同累积塑性应变条件下,温度越低,冻结土石混合体的动弹性模量越大。另外温度越低,数据点的密度越大,说明达到对应累积塑性应变所需要的循环次数越多。对于温度在-10 ℃(图6黑色曲线)和-5 ℃(图6蓝色曲线)条件下的试样,在5%应变条件下,随着应变的增大,动弹性模量有增大的趋势。但相对于-15 ℃(图6 红色曲线)的试样,动弹性模量先增大到一定峰值而后逐渐减小,与-10 ℃和-5 ℃变化趋势不同,这主要是达到相同应变所需要的循环次数不同导致的。由于-15 ℃条件下,土石混合体达到相同应变所需的循环次数增多,导致试样内部裂纹扩展增多,从而降低试样的动弹性模量。
-15 ℃条件下动弹性模量随累积塑性应变的增大先增大后减小,初步认为可能是由于土石之间裂纹的开展导致。循环荷载条件下土石之间更易发生相对运动,循环次数越多,土石界面更易被破坏而产生微裂缝,土石之间的咬合和嵌固作用下降,这就导致其动弹性模量降低。另外,在加载过程中随着时间的推移试样本身会产生热量,内部温度会有增大趋势[25],导致冰晶的融化,冰的胶结作用降低,进一步降低了土石之间的嵌固作用[26];其次受设备保温效果影响,达到相同的累积塑性应变,-15 ℃所需要的循环次数多,加载时间长,试样表面温度有所升高,导致试样的弹性模量后期呈现下降的趋势。
粗粒含量作为冻结土石混合体最为关键的参数之一,下文讨论了含石量与冻结土石混合体弹性模量的规律。图7是三种幅值应力条件下不同含石量的动弹性模量与累积塑性变形之间的关系,可见当累积塑性应变小于3%时,含石量30%试样的动弹性模量小于含石量40%和50%试样的动弹性模量。峰值应力为1.5 MPa 和2.0 MPa 时,40%含石量的试样大于50%含石量试样的动弹性模量;而当峰值应力为2.5 MPa 时,在初始循环阶段含石量40%的试样明显小于含石量50%试样的动弹性模量,而随着累计塑性变形的增大,含石量40%的试样明显大于含石量50%试样的动弹性模量。可见随着含石量的增大其动弹性模量有增大趋势,但在本次试验中极大值在40%与50%之间,受篇幅限制并未进一步开展相应的试验探究含石量50%含石量的增长规律。

图7 不同幅值应力条件下-10 ℃动弹性模量与累积塑性应变之间的变化情况Fig. 7 Variation between dynamic modulus of elasticity and cumulative plastic strain at -10 °C for different amplitude stress conditions: 1.5 MPa (a), 2.0 MPa (b), 2.5 MPa (c)
随着含石量的增大,动弹性模量增大的趋势原因可能是块石的弹性模量明显大于冻土的弹性模量,块石含量越大,试样的动弹性模量越大。随含石量的继续增大,动弹性模量可能会出现峰值点。但40%与50%含石量的动弹性模量近似,可见弹性模量的增长并不是线性增大的,这可能是受控于土石的咬合和嵌固作用,由于土与石之间的压缩系数不同,这就导致在加载过程中,冻土的变形量大,而块石基本不发生形变,块石与冻土的胶结和嵌固作用更易被破坏,进而导致其动弹性模量降低。
2.3 累积塑性应变随循环次数变化的规律
为了更进一步探讨累积塑性应变的规律,同时更直观地反映低温土石混合动应力-应变滞回环从稀疏变密集再到稀疏的过程,下文探究了累积塑性应变与循环次数之间的关系。通过图8累积塑性应变与循环次数之间的关系,发现低温土石混合体的累积塑性应变可分为三个阶段:初始变形阶段,稳定变形阶段和破坏阶段[图8(a)]。同时对比2.2节发现,其初始变形阶段对应了滞回环呈不闭合的椭圆形的阶段,稳定变形阶段对应了柳叶形的阶段,破坏阶段对应了扁长椭圆形阶段(图9)。在初始变形阶段应变随着循环次数增大,累积塑性应变快速增加。这是由于轴向荷载的作用,试样内部微裂缝闭合和试样压实过程中发生轴向应变,其微裂纹是指由于冻胀而引起的裂纹[27]。而后进入稳定变形阶段,随着循环加载次数的增加累积塑性应变增长相对缓慢,且与循环次数线性关系;线性阶段结束后,进入破坏阶段,累积塑性应变快速增大。该阶段试样已发生明显破坏。为了进一步阐明累积塑性应变的过程,下文结合峰值应力和温度,进一步探讨累积塑性应变的规律。
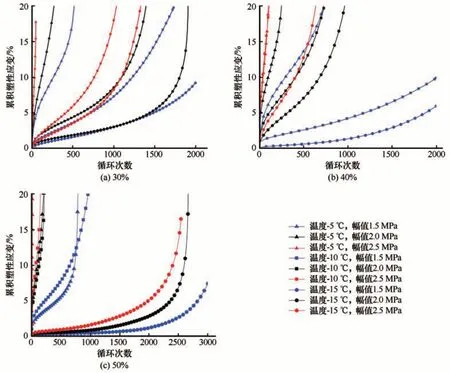
图8 不同含石量条件下的累积塑性应变与循环次数之间的关系Fig. 8 The relationship between cumulative plastic strain and number of cycles at different stone content:30% (a), 40% (b), 50% (c)

图9 累积塑性应变与循环次数变化的三阶段和滞回环特征图Fig. 9 Cycle number change and hysteresis loop feature diagram (a), and three stages of cumulative plastic deformation (b), (c), (d)

图10 改进的Monismith模型40%含石量循环次数与累积塑性应变的拟合结果Fig. 10 Results of fitting the improved Monismith model of the number of cycles with 40% stone content to the cumulative plastic strain
相同条件下,幅值应力越大,达到破坏应变所需的循环次数越多。图8中在相同循环加载次数条件下,幅值应力2.5 MPa 条件下对应的累积塑性应变最大,其次是幅值应力2.5 MPa,最后为幅值应力1.5 MPa,即幅值应力越大,相同循环次数下,累积塑性应变越大。
累积塑性应变随循环次数变化的三阶段如图9(a)曲线所示:①在循环次数较少时处于初期变形阶段,累积塑性应变随循环次数快速增大。②当循环加载次数达到318时,进入稳定变形阶段,累积塑性应变的增长放缓,呈现明显的线性特征。为了更好地描述第二阶段的变形规律,引入稳定变形斜率k,稳定变形阶段作为试样抵抗动荷载的关键阶段,该阶段的斜率在一定程度上决定了试样从稳定变形阶段向快速变形阶段转变所需要的循环次数,斜率越低所需的循环次数越多,试样抵抗动荷载的能力越强。表2 给出了不同条件下,低温土石混合体在循环荷载作用下的稳定变形阶段斜率k。③当循环次数大于1 676 时,进入快速变形阶段,其塑性变形随循环次数增大而快速增大,曲线的斜率明显增大。在幅值应力为2.5 MPa 条件下,曲线快速越过稳定变形阶段进入破坏阶段,尤其是-5 ℃和-10 ℃条件最为明显,在破坏阶段裂纹扩展速度快速增加,100 次循环加载下试样应变已超过15%,试样已破坏。
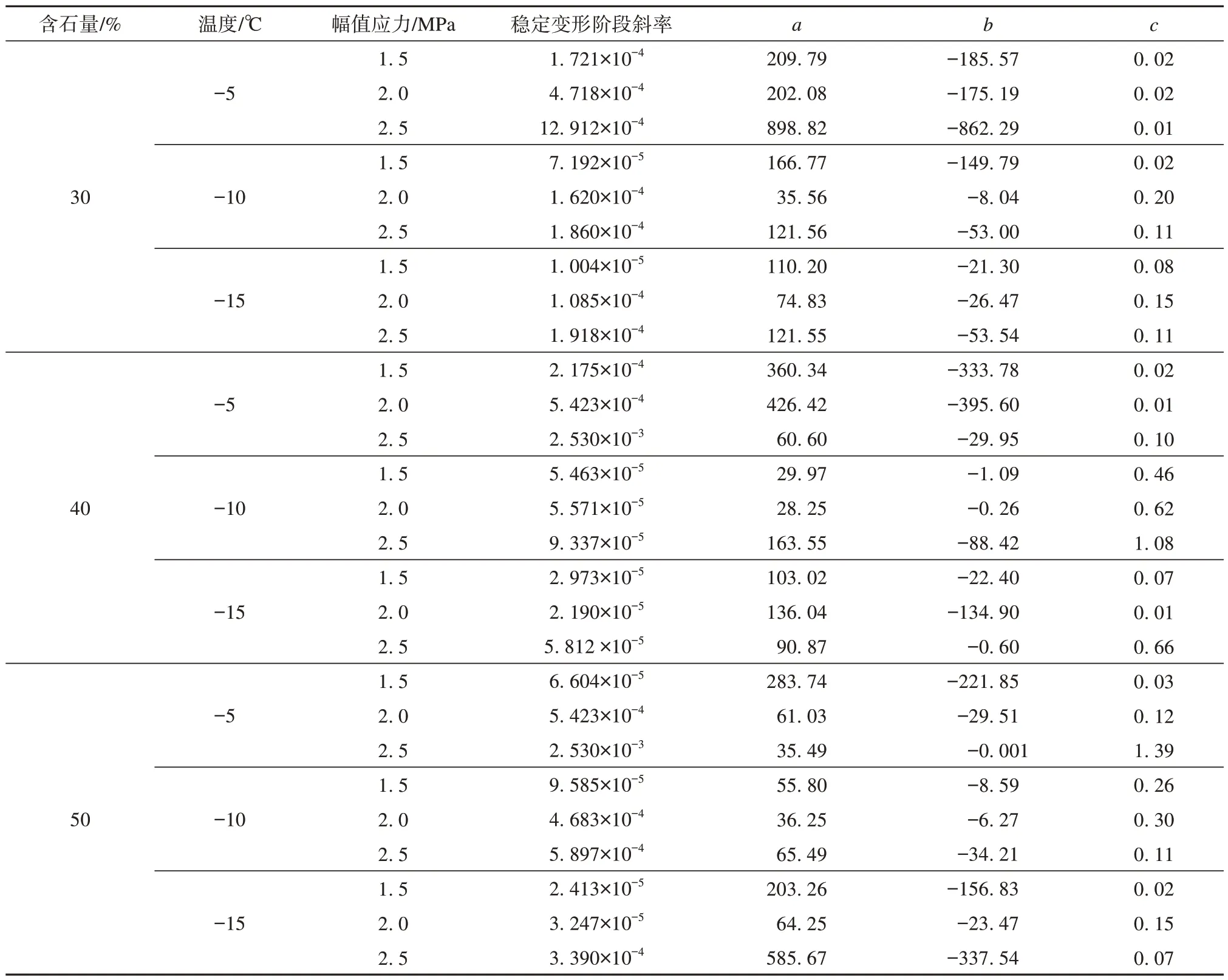
表2 不同条件下稳定变形阶段的斜率和改进Monismith指数模型参数Table 2 Slope of stable deformation stage under different conditions and parameters of improved Monismith exponential model
为了更好地描述冻结土石混合体累积塑性应变的变化规律,前人提出了Monismith 模型[28]来预测累积塑性应变的变化规律(式2),该模型因其简易而被广泛运用。结合本文试验,运用Monismith模型对-10 ℃含石量40%试验结果进行拟合结果如图11(c)所示,可见其拟合度较差,无法准确呈现累积塑性应变随循环次数增加的三个阶段。
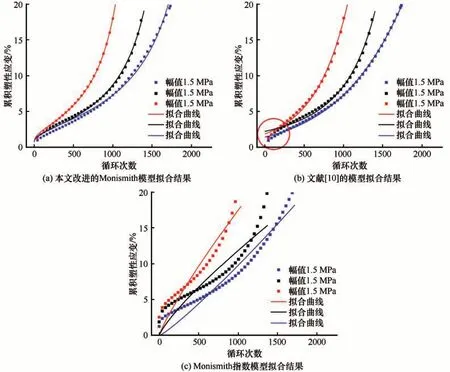
图11 不同模型下累积塑性应变与循环次数的拟合结果Fig. 11 Fitting results for cumulative plastic strain versus number of cycles for different models: results of the improved Monismith model fit (a), model fitting results from References [10] (b), Monismith exponential model fit results (c)
Monismith指数模型为
式中:ε为累积塑性应变;N为循环次数;参数a和b与应力水平和土体性质有关。
Zhang 等[10]在研究低温条件下碎石土的三轴动力学特性时提出了修正的Monismith 模型[式(3)],以期更好地呈现累积塑性应变的特征。但在本文试验结果中拟合度较差,通过图11(b)可知,该模型虽在稳定变形阶段和破坏阶段有较好的拟合结果,但是无法呈现初期累积塑性变形的快速增长趋势。
式中:ε为累积塑性应变;N为循环次数;参数a、b和应力水平、土体性质有关。
针对本文试验的累积塑性应变特征,提出了改进Monismith 指数模型[式(4)],描述冻结土石混合体的累积塑性应变的演化特征。
式中:ε为累积塑性应变;N为循环次数;参数a、b和c与应力水平、土体性质和温度相关。当a= 0 时,模型为Monismith 模型,其中N为正整数,最小值为1。
采用试验结果来确定改进Monismith 模型参数,图10 给出了含石量40%条件下的拟合结果,可见其能够较好拟合低温条件下土石混合体的累积塑性应变特征,并能体现累积塑性变形随循环次数变化的三个阶段,其拟合曲线R2均在0.98以上。
2.4 改进Monismith 模型参数与试验条件的相关性
为了探究不同试验条件下,含石量、温度、峰值偏应力对改进Monismith 指数模型参数的影响。本文结合实际拟合得到的结果,通过统计学的方法,利用SPSS 对表2 中的参数a、b和c进行斯皮尔曼相关性分析和偏相关性分析,探究参数与含石量、温度和峰值应力的相关性,进而明确改进Monismith指数模型中参数受试验条件影响规律。斯皮尔曼相关系数以Charles Spearman 命名的相关系数,是评估两个变量之间依赖性的关键指标。斯皮尔曼相关系数能够准确迅速地确定两个变量之间的显著性关系,在金融、医学、网络等方面广泛运用[29]。且因其不需要变量服从正态分布,适用范围广。偏相关分析作为一种多变量相关性分析方法,它可以在控制一个变量的条件下,研究另外两个变量之间的相关性,即在剔除其他因素影响的条件下,衡量两个变量之间相关性的方法[30-31]。以上两种分析结果中斯皮尔曼相关系数rs和偏相关系数rz的绝对值越接近于1 表明两个变量相关性越高(r>0 正相关,r<0代表负相关),P值用于衡量相关性的显著水平,P<0.05 表示两个变量之间显著相关,P<0.01 表示2个变量之间极显著相关。
利用斯皮尔曼相关性分析,对含石量、温度和应力水平进行相关性分析,得到表三中的结果。含石量与参数b两个变量之间的斯皮尔曼相关系数rs为0.501,P=0.00779(P<0.01),可以得出两变量之间的相关性是极显著的。结合斯皮尔曼相关系数的定义可知含石量与参数b的相关性呈显著正相关。说明改进的Monismith 模型中参数b受含石量变化的影响。含石量与参数c两个变量之间的斯皮尔曼相关系数rs=0.4957,P=0.00855(P<0.01),可以得出两变量之间的相关性是极显著的。结合斯皮尔曼相关系数的定义可知含石量与参数c呈极显著正相关。说明改进Monismith 模型中参数c受含石量变化的影响。但由于含石量与参数c的rs小于含石量与参数b的rs,可见含石量与参数c的相关性小于与参数b的相关性,即含石量的改变对参数b影响更为明显。
另外通过表3,可见温度与参数a、b和c的P值均大于0.05,幅值应力与参数a、b和c的P值同样大于0.05,无法满足合斯皮尔曼相关系数中P值的定义,可见温度和幅值应力与参数a、b和c之间的显著性弱。考虑到斯皮尔曼相关性分析会受到其他变量的影响,不能准确反映两个变量之间的关系。偏相关分析通过控制变量的方法,量化两个变量之间的相关性[30,32]。通过偏相关分析(表4)发现,在控制含石量条件下,温度与参数a的偏相关系数为rs=-0.45217,P=0.04(P<0.05),温度与参数a呈现显著负相关,可见参数a受温度的影响较为明显;在控制温度的条件下,含石量与参数c的偏应力系数rs=0.49086,P=0.01089(P<0.05),含石量与参数c呈现显著正相关;在控制轴向幅值的条件下,含石量与参数c的偏应力系数rs=0.49833,P=0.00957(P<0.01),含石量与参数c呈现显著正相关。综上,在控制含石量的情况下,Monismith 模型中的参数a与温度呈现一定的相关性,可见参数a受温度的影响较为明显。斯皮尔曼相关性分析中已得到含石量与参数b和c呈显著正相关性,而在偏相关分析中得到含石量与c仍存在显著相关性。另外,在偏相关分析的条件下,轴向幅值与a、b、c的P值均大于0.05,由此可见轴向应力与参数a、b和c的相关性弱,可见该模型在轴向力改变的条件下,对参数a、b和c的影响小,说明该模型具有更广的适用性。另外,参数c与试验条件的相关性弱,作为拟合测试的指数参数,随试验条件变化,参数c的变化幅度小,难以探究其与试验条件的相关性。
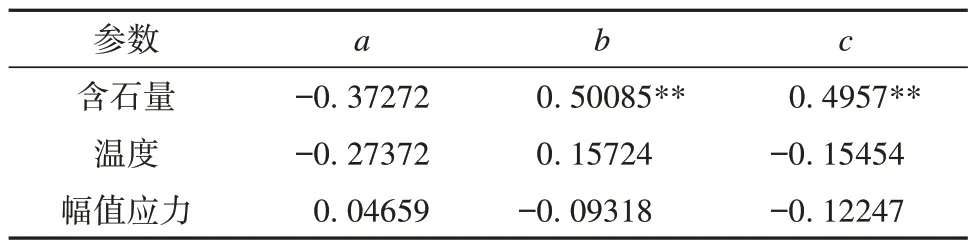
表3 不同实验条件、不同模型参数下斯皮尔曼相关系数值Table 3 Spearman phase relationship values under different experimental conditions and different model parameters

表4 含石量、温度和轴向幅值与a、b、c参数偏相关分析结果Table 4 Results of bias correlation analysis of stone content, temperature and axial amplitude with parameters a, b and c
综上所述,含石量与参数b和参数c的相关性呈显著正相关,相较而言含石量对参数b的影响更为明显;在偏相关分析中,剔除含石量的影响,参数a受温度的影响较为明显。峰值应力的改变对试样模型参数a、b、c影响小,可见该模型在不同的峰值应力条件下有更好的适用性。
3 结论
本文通过开展-5 ℃、-10 ℃和-15 ℃、不同含石量条件下单轴循环加载试验,讨论了冻结土石混合体在循环荷载下的动力学特性,比较了不同条件下累积塑性应变和动弹性模量的变化规律,得出如下结论:
(1)循环荷载作用下动应力-应变曲线表现出疏-密-疏的三个阶段。循环加载起始阶段,滞回环的相对位置较为稀疏,这是由于初始循环阶段中土石混合体颗粒间压密和微裂纹闭合。随着循环加载次数的增大,单个循环对应的塑性变形量先逐渐变小,滞回环的相对位置表现出从稀疏变转为密集的规律,其机理与微裂纹闭合后提升的抵抗动荷载能力有关。而后滞回环的相对位置呈现出由密集转变为稀疏的规律,这与土颗粒冰块石组成的胶结体发生颗粒滑移,导致整体塑性变形增大有关。并在此基础上总结了滞回环相对位置的演化规律:滞回环初期为不闭合的椭圆形,随着循环加载次数的增大逐渐接近柳叶形,最后为近似闭合的扁长椭圆形。
(2)比较了动荷载作用下动弹性模量的变化情况,随着含石量的增大,弹性模量呈现增大的趋势,而在当含石量40%与50%时其增大趋势不明晰。相较于含石量的变化对动弹性模量的影响,温度对动弹性模量的影响更显著,随着温度的降低,冻结土石混合体的动弹性模量逐渐增大,且温度越低,动弹性模量的增大越明显,其细观机理与冻土和块石之间的咬合和嵌固作用有关。另外,-15 ℃条件下动弹性模量随累积塑性应变的增大先增大后减小,这可能与循环次数增大后,试样温度变化有关。
(3)比较了不同条件下,循环次数与累积塑性应变之间的变化规律,幅值应力越大,达到破坏所需的循环次数越少。并提出了累积塑性应变与循环次数的改进Monismith 指数模型,通过实验数据验证了该模型的合理性,给出不同温度、含石量和峰值应力条件下的模型参数值。同时运用统计学中斯皮尔曼相关系数和偏相关分析,明确了改进Monismith 指数模型中的参数b值的受含石量的影响明显,参数a受温度的影响较为明显,峰值应力的改变对试样模型参数a、b、c影响小。

