一种数据驱动的飞行仿真参数辨识方法*

耿 宏，李沅锴，钱文高

（中国民航大学电子信息与自动化学院，天津 300300）

0 引言

目前飞行仿真大多应用特定机型飞行数据包，快速存取记录器用于实时记录数以百计的飞行参数［1］，QAR 数据中包括飞机飞行环境实时数值、飞机实时状态数值、系统实时状态记录和部件实时状态记录等。通过分析QAR 数据同样可以清楚地掌握飞机飞行整个过程，故应用飞机运行数据进行飞行仿真研究具有重要意义。

近年来，多位学者针对于特定机型的飞行参数辨识与建模展开研究。杨媚等基于无人机试飞数据辨识出气动模型［2］；ZHOU 等对巡航阶段无人机控制进行了研究［3］；蒋启登应用飞行数据建立了舰载机的拦阻载荷统计模型［4］；李亚东等基于飞行测试数据辨识电动飞机气动焦点［5］；颜巍等以大型民机机载传感器采集运动参数为基础，建立了在尾旋运动条件下的气动力矩系数模型［6］；陈仁良等针对直升机的参数辨识方法作了相应研究［7］；赵令公等为翼伞系统飞行参数辨识作出了贡献［8］。以上提到方法都是针对于某个特定机型展开研究的。

应用神经网络等黑箱算法辨识飞行参数这一领域，国内外学者也有相应研究。王超等基于机器学习方法，实现了对飞机气动力数据的高精度拟合［9］；柴聪聪等应用卷积神经网络预测了结冰翼型气动参数［10］；MAHAJAN 等基于循环神经网络（RNN）估计了飞机空气动力导数［11］；韩建福等将双BP 神经网络引入扑翼飞行器飞行参数辨识［12］。以上神经网络算法并不能定量表达飞行参数之间相关性。

综上所述，目前飞行参数辨识多以特定飞机机型展开研究，现阶段主流的神经网络辨识方法虽有较高仿真精度，但无法定量表达参数关系，且现有飞行参数经验公式针对于不同飞机机型无法达到较高拟合度。本文目的是基于QAR 数据探索一种简单、高效、可适用于任何机型的飞行参数辨识方法，并具有较高仿真精度，且针对不同机型飞行参数可得到对应经验公式，为此提出一种基于QAR数据的改进多项式拟合方法辨识飞行参数。

1 算法原理

1.1 参数关系确定

式中，ρXY为参数X 和参数Y 的斯皮尔曼等级相关系数；n 为参数向量中元素个数。

斯皮尔曼等级相关系数通常用于衡量两个参数的相关程度，适用于数据量较大，且数据总体分布未知的情况，飞行参数的数据分布情况通常是没有办法确定的。因此，本方法利用等级相关系数确定飞行参数之间相关性，经算法求得的等级相关系数越大，证明两个参数相关性越高，应用相关性高的参数进行参数辨识可有效提高仿真精度。

1.2 权重系数设计

针对多项式拟合算法中不同输入参数与被拟合参数相关性有差异，提出一种考虑输入参数权重的改进多项式拟合算法，该算法通过计算输入参数与被拟合参数的斯皮尔曼等级相关系数ρ1，ρ2，ρ3，…，ρn，利用斯皮尔曼等级相关系数计算权重系数，等级相关系数可表示输入参数与被拟合参数的相关性，相关性越高，等级相关系数绝对值就越大，所以，在拟合时所占权重应该越高。故提出应用斯皮尔曼等级相关系数计算的权重系数：

式中：εi为权重系数；ρi为斯皮尔曼等级相关系数；n为输入参数个数。

1.3 算法改进过程

本方法通过计算输入参数的权重系数，将输入参数所占比重按相关性分配，相关性高的参数在算法计算中所占比重大，相关性低的参数所占比重小，目的是为提高算法仿真精度，故参考文献［13］将基于最小二乘法的多项式拟合算法加以改进，具体改进过程如下：

α 表示一个飞行参数数据集，V 表示另一个飞行参数数据集，L 表示被拟合参数数据集，给定一点坐标（αt，Vt），t=1，2，3，…，q，t 表示选取飞行参数数据集中元素对应序号，q 大于0 且小于等于选取飞行参数数据集元素总数，m 表示α 拟合次数，n 表示V 拟合次数，CL（α，V）表示二元多项式拟合出的飞行参数经验公式。通过改进方法拟合飞行参数的过程如下：

分别计算α，V 与被拟合参数L 的斯皮尔曼等级相关系数：ραL，ρVL。通过等级相关系数计算两个参数在算法中的权重系数：

即

对系数矩阵进行求解，首先构造系数矩阵多元函数：

设

由式（9），如果函数满足极小值点等于0，那么，

将式（10）每个等式两边同时除以2，并写成矩阵形式得：

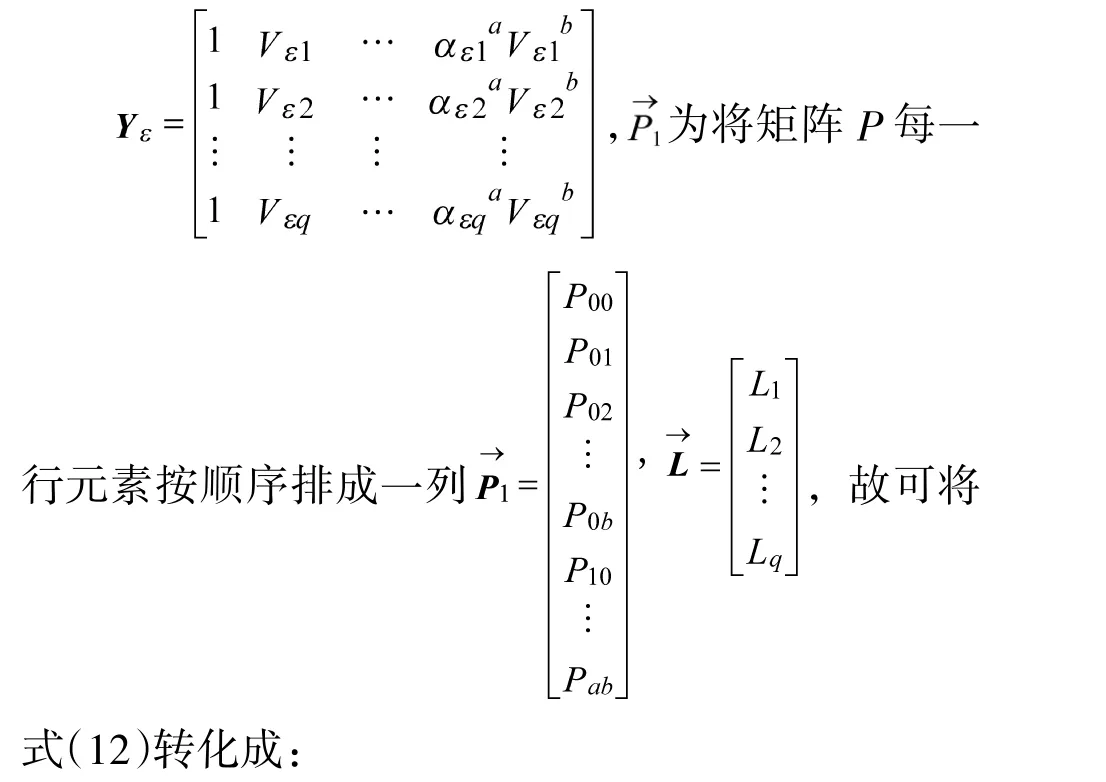
由式（11）化简得到范德蒙矩阵：

将式（12）记为：

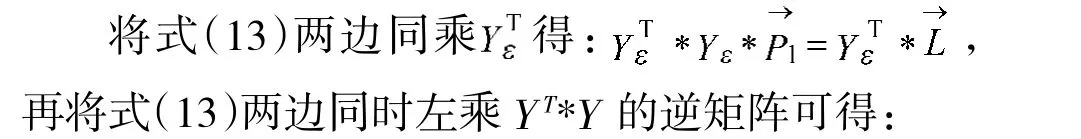
2 仿真验证

应用QAR 数据B-1833_20181224 航段中730s～6 908 s 的迎角、空速数据拟合升力系数为例验证本文改进方法，首先令式（5）中：

然后计算迎角、空速倒数与升力系数的斯皮尔曼等级相关系数，数据集等级向量是将数据集中元素从大到小排列，确定每个元素对应排列序号，如果其中几个元素大小相同，它们的排列序号均为这几个元素对应大小序号的平均数，再将数据集中元素替换成其对应的排列序号，基于此得出数据集等级向量。

令迎角数据集等级向量为1×6 179 的行向量：

空速倒数数据集等级向量为1×6 179 的行向量：

升力系数数据集等级向量为1×6 179 的行向量：

分别计算迎角、空速与升力系数的等级差向量：

将其代入式（2）：

将计算结果代入式（4）计算权重系数：

然后分别设置多项式中迎角、空速倒数两个参数需要拟合的次数a=2、b=2，将其代入式（7）并求得式（13）中：

将Yε代入式（14）求得：

为验证方法有效性，利用改进多项式拟合与多项式拟合算法进行对比，如图1 所示，改进多项式拟合效果优于多项式拟合算法，改进算法与原算法误差对比结果如下页表1 所示。

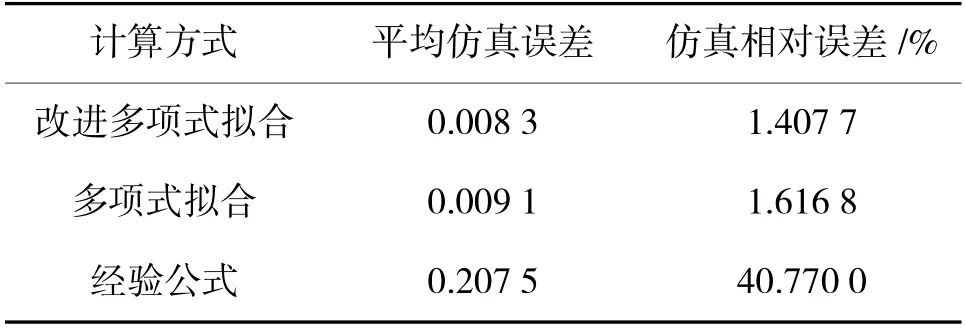
表1 改进算法与原算法升力系数误差表Table 1 Lift coefficient error table of improved algorithm and original algorithm

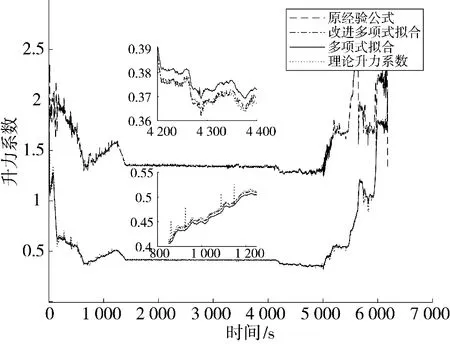
图1 改进算法及原算法与升力系数对比图Fig.1 Comparison chart of improved algorithm，original original algorithm and lift coefficients

将拟合出的升力系数经验公式代入飞机六自由度运动学模型进行仿真验证，由环境模型仿真出的飞机爬升阶段至巡航阶段外部环境变化与实际QAR 数据记录外部环境对比如图2 所示，从图中可以看出，仿真外部环境风速风向与真实QAR 数据记录飞机飞行时外部环境趋势相近，相近的外部环境可以使仿真结果更接近于实际飞行过程。

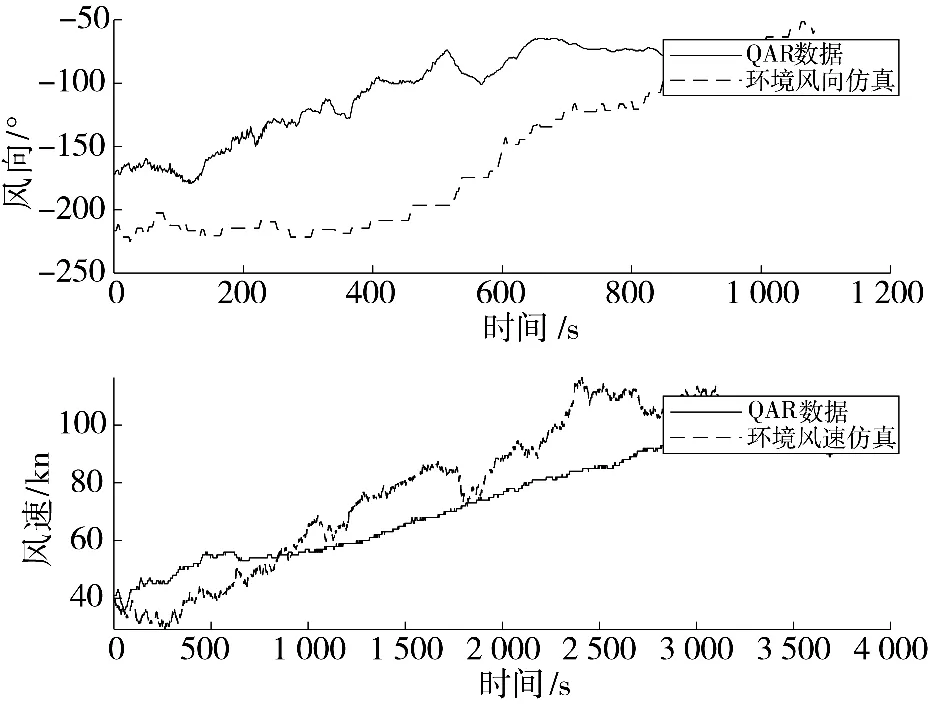
图2 仿真外部环境与QAR 数据对比图Fig.2 Comparison chart of simulation external environment and QAR data

通过运动模型仿真实际飞行中飞机由5 000 ft爬升至9 000 ft，空速由234～250 kn 的过程，验证改进算法，原算法与原经验公式的仿真误差，仿真误差如表2 所示。

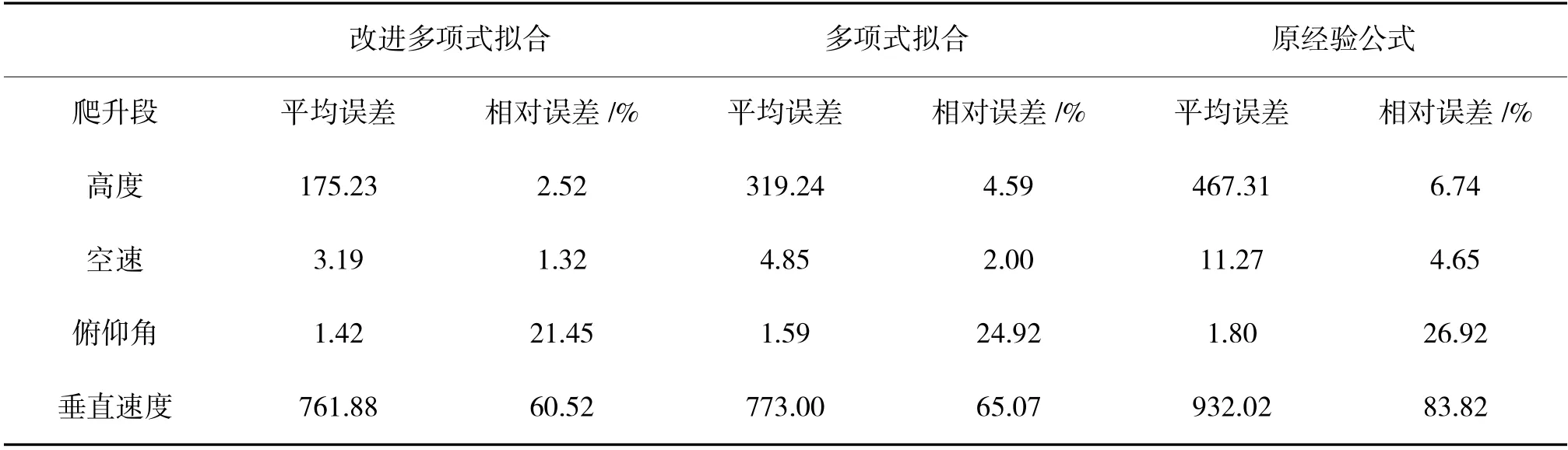
表2 爬升段误差表Table 2 Error table of climbing phase

爬升段仿真结果如图3 所示。

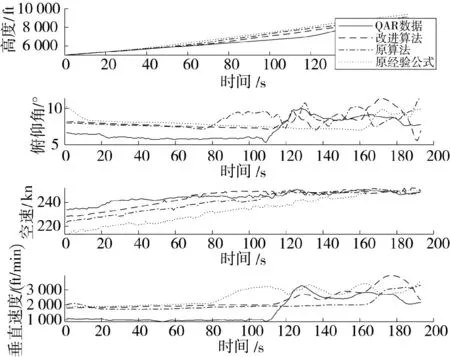
图3 爬升段仿真与QAR 数据对比图Fig.3 Comparison chart of climbing phase simulation and QAR data

由表2 结果可知，爬升段高度与空速仿真结果较好，俯仰角与垂直速度仿真偏差较大。由图3 可以看出，垂直速度偏差较大原因是在110 s 时，真实飞行QAR 数据高度有明显的斜率上升，垂直速度会出现突变，而仿真高度变化的斜率大致恒定，因此，偏差较大，俯仰角仿真偏差较大原因是仿真外部环境无法与真实外部环境完全相同。因此，俯仰角会受到风速和风向干扰产生误差，由仿真结果来看，爬升段仿真与实际QAR 数据对比参数变化趋势一致。

通过运动模型仿真实际飞行中飞机在31 200 ft高度巡航，空速285 kn 保持的过程，验证改进算法，原算法与原经验公式的仿真误差，仿真误差如下页表3 所示。

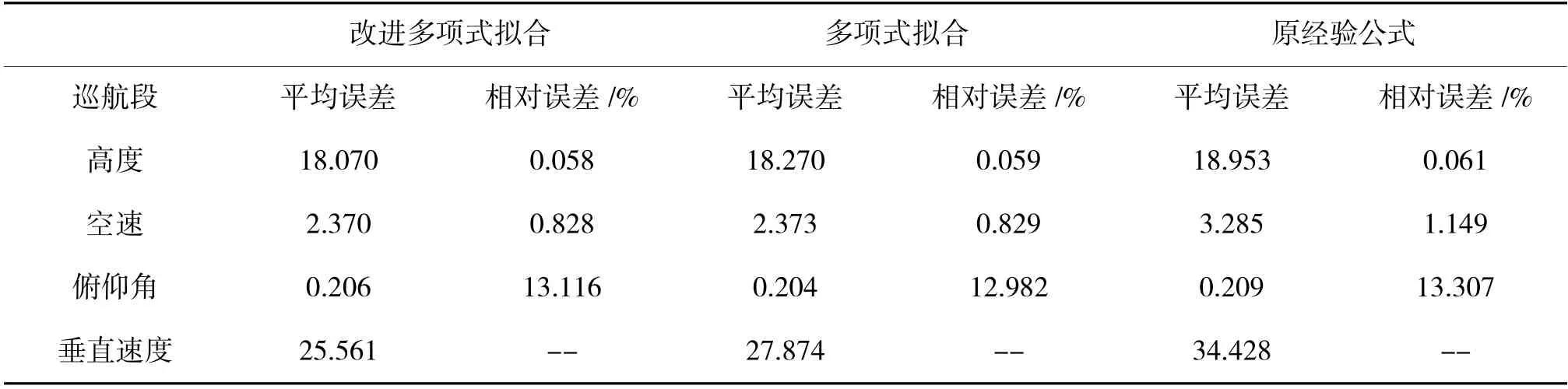
表3 巡航段误差表Table 3 Error table of cruise phase

巡航段仿真结果如图4 所示。

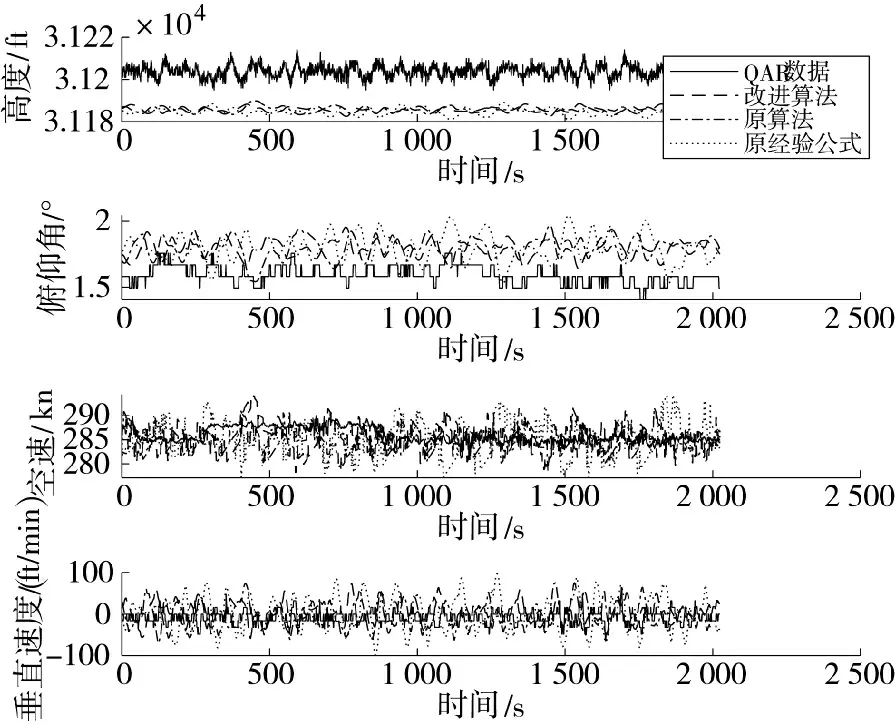
图4 巡航段仿真与QAR 数据对比图Fig.4 Comparison chart of cruise phase simulation and QAR data

由表3 结果可知，改进算法与原算法在巡航段仿真效果大致相同，因实际巡航段垂直速度中存在为零情况，故巡航段垂直速度相对误差无法求得。由图4 可知，巡航段仿真俯仰角稳定在1.8°，实际QAR 数据俯仰角稳定在1.6°，巡航段仿真高度稳定在31 182 ft，实际QAR 数据高度稳定在31 200 ft，其余巡航段仿真结果与实际QAR 数据趋势基本一致。

通过仿真验证结果表明，改进算法从总体来看可降低仿真误差，使飞行仿真更接近于实际飞行过程。

3 结论

本文改进算法相比多项式拟合算法引入不同输入参数在计算中的权重，其物理意义在于拟合过程中，与被拟合参数高度相关的输入参数权重占比应大于相关性低的输入参数，进而可使拟合结果更接近于相关性高的输入参数，基于此提高了仿真精度。