基于多级影响图的复杂机动动作最优航迹控制模型*

刘 瑛，王 俊，许红蕊，温晴川

（空军指挥学院，北京 100091）

0 引言

驾驶员是人—机—环系统的核心环节，如何从驾驶员操纵角度控制飞行风险是重要的研究方向。飞行员认为在空战对抗环境中，往往需要战术机动动作的组合运用，在这种情况下极易增大动作的偏差，从而导致风险的增大。因此，提高驾驶员对机动动作的控制能力是避免飞行风险的一项重要工作。

目前，对复杂机动动作的研究分为两个主要方向：1）如何实现对机动动作的有效控制；2）如何保证机动动作过程中的安全性及鲁棒性。针对第1 个研究方向有一系列具体方法，如机器学习方法、混合分解法、逆仿真方法等［1-5］。第2 个研究方向最典型的方法是斯坦福大学的Jeremy H.Gillula 等提出可达集（reachable set）方法，通过可达集保证机动动作控制中的安全性及鲁棒性［6］。已有方法得到的控制律多针对无人装备，如多旋翼无人机［6］、无人车辆［4］，控制律为连续时间序列控制量，但对于驾驶员却无法跟踪这样的控制量变化规律。与此同时，有人驾驶飞机驾驶员是整个操纵过程的主体，由于驾驶员的技术水平不同，机动动作偏差修正过程对于相同偏差风险程度的认识也不同，因此，在建模过程中有必要考虑驾驶员的偏好，从而使优化模型求解结果更合理。

本文将机动动作划分为彼此相连的轨迹片段，轨迹片段划分合理，则每个轨迹片段具有相同的控制量变化率，控制量变化率不但能够定量地给出机动动作过程中控制量的输入，更重要的是能够定性反映驾驶员操纵的快慢程度，对驾驶员完成一个标准的机动动作具有指导意义。同时，使用多级影响图对机动动作偏差修正过程进行建模，影响图是一种用于解决复杂决策问题的图模型，在建模过程中可以充分考虑驾驶员的偏好。文中做的主要工作包括以下3 个部分：1）使用关键点划分机动动作，每个关键点均设定标准的状态范围，从而保证机动动作为标准动作［7］；2）使用多级影响图建模考虑驾驶员偏好的机动动作偏差修正过程，并建立最优化模型；3）以典型纵向机动动作斤斗为例进行分析，给出了不同初始状态偏差情况下的最优控制量变化率修正序列。

本文的主要创新工作包括：1）使用多级影响图建模机动动作偏差修正过程，在建模过程中考虑驾驶员偏好；2）以控制量变化率作为优化变量，优化结果能够使驾驶员对机动动作的偏差修正过程有更明确的认识，从而更好地辅助驾驶员进行决策。

1 多级影响图决策建模

多级影响图是一种用于解决复杂决策问题的图模型［8］，它表达了变量间的依赖关系、条件独立关系和决策者的偏好。使用多级影响图的优点在于：决策者能够从图形上直观地了解相关信息，便于决策者参与决策。影响图在决策问题定性描述和定量计算之间搭建了桥梁。

驾驶员在完成机动动作的过程中，需要在关键点对当前状态参数进行判断［7］，关键点是指驾驶员完成机动动作过程中需要进行状态参数判断的关键位置，驾驶员需要通过一系列操纵使状态参数在关键点达到标准状态参数的要求，如果状态参数在关键点出现偏差，需要通过操纵进行修正。偏差的修正过程可以描述为：1）观测飞机当前状态；2）评估当前状态与标准状态的偏差；3）预测通过可能的操纵会在下一个关键点达到的状态并对状态进行评估；4）选择最优的操作，返回1）。驾驶员通过不断重复以上步骤来完成一个标准的机动动作。从以上步骤可以看到，驾驶员完成机动动作的过程是发现偏差、评估偏差、修正偏差的过程。在这一过程中，飞行经验丰富的驾驶员能够驾驭的偏差裕度比新驾驶员大得多，因此，对于相同的偏差不同的驾驶员对风险的评定也不同。所以，在确定机动动作最优控制量变化率修正序列时，考虑驾驶员对风险的承受能力或者称为驾驶员的偏好，能够使计算的结果更具针对性。

使用多级影响图建模机动动作的偏差修正过程，如下页图1 所示。假定机动动作有个关键点，图中4 种类型结点的含义如下：

1）矩形为决策结点，表示驾驶员依据关键点标准状态与实际状态的偏差采取的机动动作修正策略；

2）椭圆形为机会结点，表示关键点状态偏差对应于不同风险等级的概率；

3）圆角矩形为确定型结点，表示风险状态参数在关键点的实际值；

4）菱形为价值结点，表示对机动动作的风险进行评估，也就是对驾驶员机动动作的偏差修正序列进行评估。

从图1 可以看到，整个机动动作包括j 个关键点，j-1 个阶段。“风险状态参数”结点表示关键点风险的决定性参数，由状态参数的实际值和标准值共同决定。“风险评估”结点得到当前结点处于不同风险等级的概率，由当前结点的风险状态参数和上一个关键点所处风险等级概率共同决定。“机动决策”结点表示驾驶员在当前关键点的偏差修正策略，由上一个关键点的偏差修正控制量、关键点的实际状态、关键点的风险状态参数、关键点的风险评估值决定。“阶段风险评估”结点表示当前关键点所处阶段的风险值。不同阶段的风险值线性求和得到机动动作总的风险值，即“机动动作风险评估”结点的输出。依据多级影响图构建的驾驶员序列机动决策过程构造优化模型，优化目标为整个机动动作风险值最小，优化结果为控制量变化率修正序列。

2 机动动作最优航迹控制模型

依据多级影响图构建驾驶员机动序列决策优化模型，下面分别讨论多级影响图中的风险状态参数、风险评估结点对应的关键点处于不同风险等级的概率以及关键点的风险值。

2.1 风险状态参数

第j 个关键点的实际状态参数与标准状态参数的差值决定风险状态参数用RSj标识，第j 个关键点对应风险状态参数包括：dj为位置偏差；ΔVj速度偏差；Δθj为速度方向偏差；Δαj为迎角偏差，具体表示为：

2.2 风险等级概率

依据多级影响图，风险评估结点所对应的关键点处于不同风险等级的概率，由当前关键点状态偏差以及上一个关键点所处的不同风险等级的概率确定，具体表示为：

条件概率依据具体机动动作，通过驾驶员对关键点风险等级与风险状态参数概率分布情况的统计得到［7］。

2.3 阶段风险值

其中，ωk表示风险等级Ck时风险状态参数的权重，不同的机动动作不同风险等级对应的风险状态参数的权重不同。r（·）表示风险函数，风险函数表示风险状态参数偏差造成的风险，将不同风险函数造成的风险进行标准化处理：风险状态参数在标准偏差内，风险值设定为0，若超过标准偏差，则风险值增大，最大风险值为1。偏差的范围与风险值的对应关系依据驾驶员的经验确定，图2（a）、图2（c）、图2（e）、图2（g）给出的是成熟的驾驶员对于状态参数偏差对应风险值的认知，对于新驾驶员能够驾驭的状态偏差的范围要小，如图2（b）、图2（d）、图2（f）、图2（h）所示，通过左右两图的对比可以看到不同驾驶员对于风险认知的差异，体现了驾驶员的偏好。

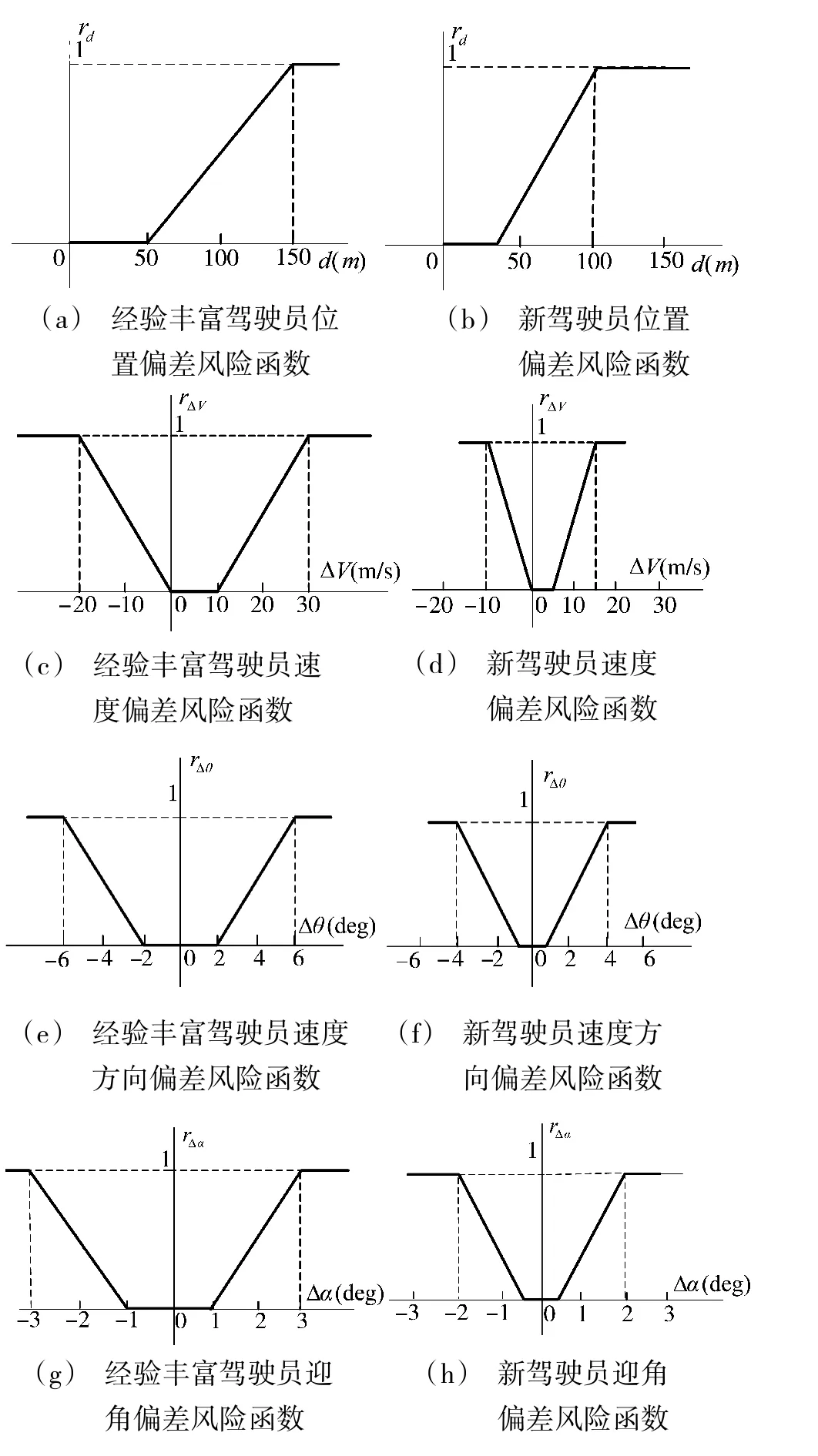
图2 状态偏差的风险函数Fig.2 The risk functions of the state deviation

与图2 对应的风险状态参数的风险函数如下所示：

2.4 构建优化模型

考虑驾驶员偏好的机动动作最优航迹控制模型的目标函数如下所示：

其中，n 为机动动作关键点个数；k 为风险等级；W表示权重系数。目标函数由两部分组成：第1 部分表示阶段风险值的大小；第2部分表示相邻轨迹片段控制量变化率的差值，m 为轨迹片段数，Fl表示第l+1 个轨迹片段与第l 个轨迹片段控制量变化率的差值经归一化后的结果［9］。目标函数取最小值，表示机动动作的风险要小，同时，相邻轨迹片段控制量变化率差值要小，用于保证机动动作柔和操纵。最优化过程中令W＞0.5，即降低机动动作风险的优先级要高于机动动作柔和操纵的要求。

2.5 斤斗动作最优航迹控制模型

对于不同的机动动作，关键点的选取不同，对于不同的风险等级风险状态参数的权重也不同。这里使用斤斗动作具体化考虑驾驶员偏好的机动动作最优航迹控制模型。

斤斗是一类超机动、大迎角机动动作，通过发挥飞机的纵向机动性能，在垂直机动中快速改变机头指向，实现空战中占据主动态势的目的。斤斗动作中的控制量为纵向过载nz以及发动机推力，发动机推力在斤斗动作过程中为常值，需要优化的控制量为纵向过载变化率。完成斤斗动作过程中，需要关注的关键点j 有6 个［7］，在6 个关键点处对状态参数进行约束，通过优化过载变化率实现机动动作偏差的修正以及完成一个标准斤斗动作。6 个关键点分别为γ=0°、γ=30°、γ=90°、γ=180°、γ=270°、γ=360°对应的位置。飞机的轨迹片段L 为36 个，10°的航迹倾角对应一个轨迹片段。斤斗动作目标函数及其约束条件可以表示为：

其中，g（·）为质点运动方程；初始状态参数为X0；

为轨迹片段中止的判断条件；δ为一个很小的正数；以0.05 s 为仿真步长，即Δt=0.05 s。

斤斗动作的风险状态参数包括：位置偏差d、速度大小偏差ΔV、迎角偏差Δα。对于斤斗动作处于不同风险等级时风险状态参数的权重如下页表1 所示，该权重对应于式（4）中的ωk。由表1 可以看到随着风险等级的提升，ΔV 和Δα 的权重会增大，原因在于随着偏差的增大，速度和迎角可能接近临界状态，从而带来较大的风险，增大权重可以保证优先修正速度和迎角。

表1 风险状态参数的权重Table 1 The weights of the risk state parameters

斤斗动作最优航迹控制模型的求解方法采用小生境稳态遗传算法NichingSSGA［10］，该算法对于非线性时变系统具有较好的适应性。

3 仿真实例分析

本章对初始状态存在偏差的两组斤斗动作进行分析，设定进行偏差修正的为经验丰富的驾驶员。标准初始状态参数以及存在偏差的两种初始状态如表2 所示。表2 中的迎角为对应初始高度、初始速度下配平的结果。第1 种初始偏差状态：与初始标准状态相比，速度小50 km/h，高度低100 m；第2 种初始偏差状态：与标准初始状态相对，速度大50 km/h，高度低100 m。下文分析两种偏差情况下控制量变化率修正序列及其相应状态参数的变化情况。

表2 初始标准状态以及初始偏差状态Table 2 The initial standard states and the initial deviation states

3.1 仿真实例1

将斤斗动作最优航迹控制模型的初始状态设定为V0=750 km/h，高度设定为h0=1 900 m。

最优过载变化率修正序列及其对应的过载变化曲线，如图3 所示。图3 中，过载变化曲线是过载变化率的直接呈现，可以看到斤斗动作的前半段过载要小于标准斤斗动作，主要原因是过载的大小与发动机推力及升力相关，速度直接影响升力，由于初始速度小于标准速度且高度低，尽管在斤斗动作前半段发动机为加力状态，但产生的过载仍小于标准过载。

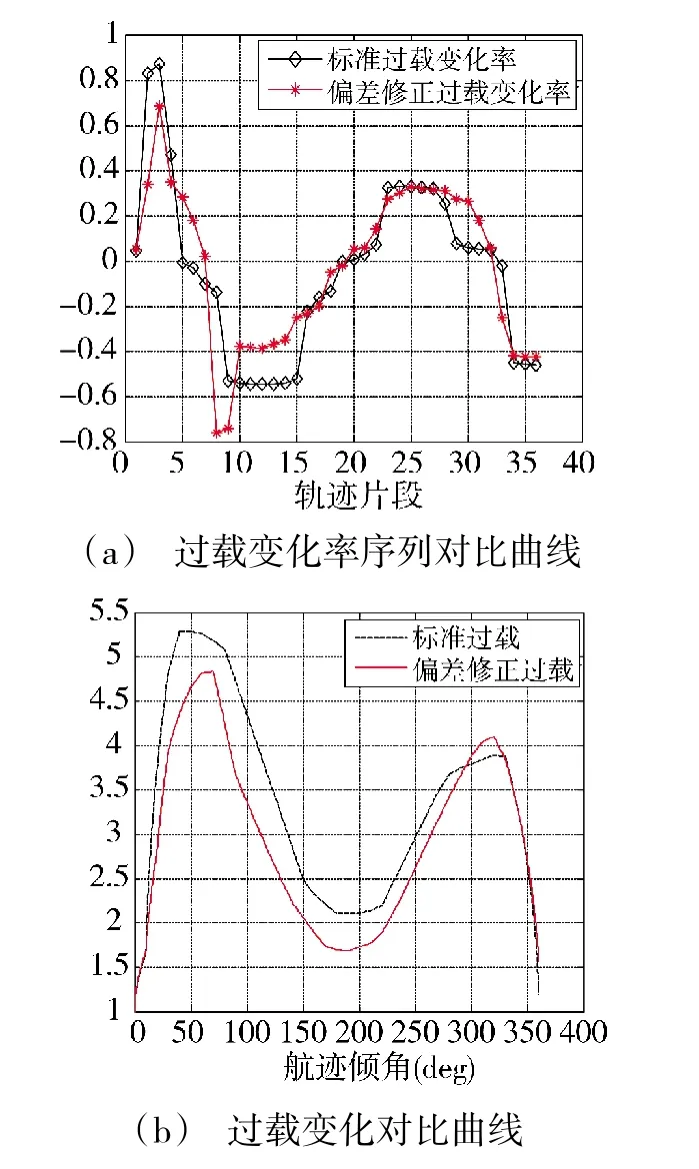
图3 修正的控制量变化曲线Fig.3 The changing curves of the corrected control quantities

与标准斤斗动作相比的位置偏差、速度偏差，以及动作航迹对比如下页图4 所示，其中，位置偏差由轨迹片段的高度偏差ΔhL以及纵向偏差ΔxL决定，图中矩形边框表示偏差正常范围。由图4 可以看到：位置偏差在初始阶段有增大的趋势，随后逐渐减小，最终在航迹倾角γ=50°时，进入正常范围；速度偏差基本处于逐渐减小的趋势，但在γ∈［50°，90°］时有小幅度的增大，之后逐渐减小，直至在γ=180°之后进入允许范围；当γ∈［10°，20°］时，速度偏差减小，但是位置偏差增大，原因在于速度偏差的减小量不能实时反映到位置偏差的减小上，需要时间的累积。

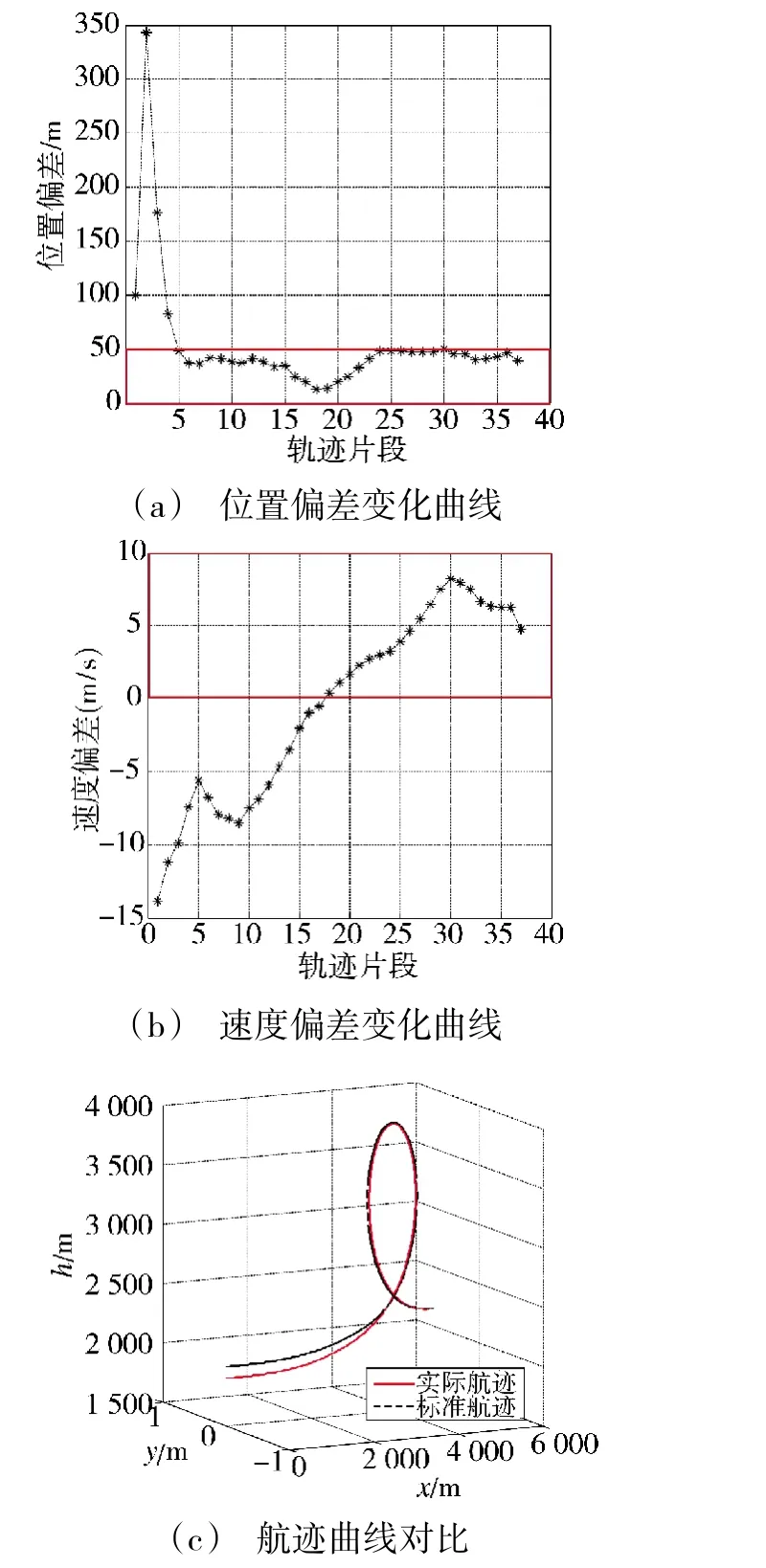
图4 风险状态参数及航迹变化曲线Fig.4 The changing curves of the risk state parameters and the trajectory

斤斗动作36 个轨迹片段的终端状态处于不同风险等级的概率如图5（a）所示，不同风险等级的初始值设定为0.25。图5（b）表示斤斗动作各轨迹片段的风险值。由图5（a）可以看到，第1 个关键点状态偏差对应的不同风险等级的概率分别为，之后风险等级2 的概率在γ=40°时，减小至0，风险等级1 的概率在γ=40°时，开始减小，并在γ=80°时减至0。由图5（b）可知，初始阶段风险值有一个增大的过程，原因在于位置偏差的增大，之后风险值逐渐减小，但在γ∈［50°，90°］时，风险值有增大趋势，原因在于速度偏差的增大，在γ=180°时，风险值减为0。由此可知，通过过载变化率的修正，机动动作的风险值最终为0。

图5 风险等级概率及风险值变化曲线Fig.5 The changing curves of the risk level probabilities and risk values

3.2 仿真实例2

将最优航迹控制模型中的初始状态设定为V0=850 km/h，高度仍然设定为h0=1 900 m。

最优的过载变化率修正序列及其对应的过载曲线如图6 所示。从图中可以看到，由于初始速度大，初始阶段过载可以达到较大值，γ=50°时的过载大于6，目的是通过增大过载，减小速度。

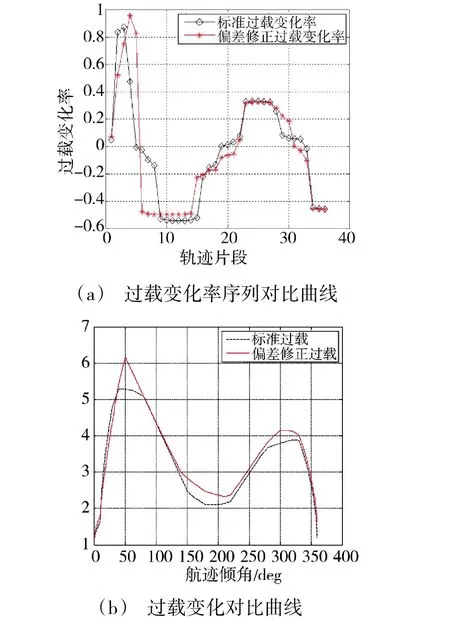
图6 修正的控制量变化曲线Fig.6 The changing curves of the corrected control quantity

与标准斤斗动作相比的位置偏差、速度偏差，以及实际航迹与标准航迹的对比如下页图7 所示。由图7 可知，位置偏差尽管在γ∈［0°，20°］时有增大的趋势，但在γ=40°时，已经进入允许范围内，速度在γ=20°时，已进入允许范围。由此可知：当初始速度大于标准速度时，由于初始状态具有较大动能，可将能量转化为偏差的修正量，偏差的修正更容易。

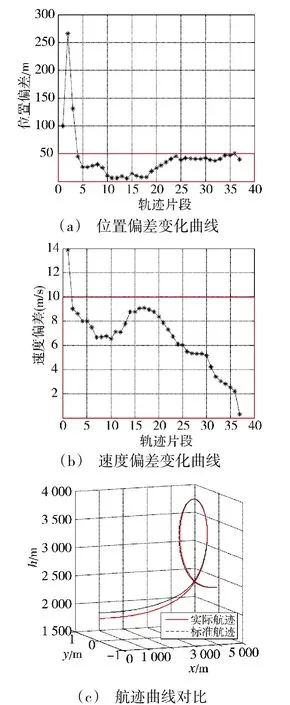
图7 风险状态参数变化曲线Fig.7 The changing curves of the risk state parameters

斤斗动作在各关键点处于不同风险等级概率变化曲线及风险值变化曲线如图8 所示。由图8（a）可以看到，第1 个关键点状态偏差对应的不同风险等级的概率分别为，之后风险等级2 的概率在γ=40°时，减小至0，风险等级1 的概率也在γ=50°时，减至0。由图8（b）可知，初始阶段风险值有一个增大的过程，原因在于位置偏差的增大，之后通过过载变化率的修正风险值逐渐减小，在γ=50°时，斤斗动作的风险值为0。

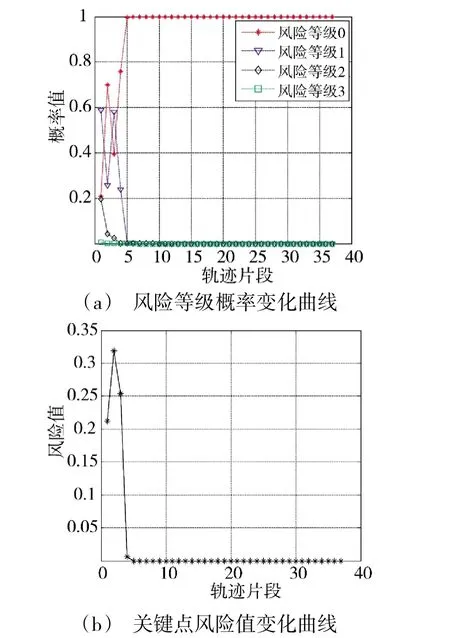
图8 风险等级概率及风险值变化曲线Fig.8 The changing curves of the risk level probabilities and risk values

4 结论

本文以复杂机动动作为研究对象，构建了基于驾驶员偏好的机动动作最优航迹控制模型，使用多级影响图对驾驶员的序列决策过程进行建模，多级影响图能够反映决策过程中各因素之间相互影响相互制约的关系。驾驶员判断的不确定性体现在状态偏差与风险值的对应关系上，具体由风险函数描述。使用小生境稳态遗传算法对优化模型进行求解，并以斤斗为例，对初始状态存在偏差的两组斤斗动作进行分析，给出了最优的过载变化率修正序列，分析了各关键点不同风险等级的概率变化情况及风险值变化情况。