基于水文过程和应力应变耦合的陕北黄土滑坡复活机理分析——以延安二庄科滑坡为例

王 康，畅俊斌，李晓科，朱文峰，卢 啸，刘 慧

（1.陕西地矿九0 八环境地质有限公司，陕西 西安 710600；2.长安大学公路学院，陕西 西安 710061）

0 引言

降雨入渗不仅是老滑坡复活的主要原因之一，也是大量工程问题的主要诱发因素，特别是持续降雨更容易导致老滑坡复活。连续降雨后，降雨入渗深度增加，使湿锋不断向下移动；此外，这将增加滑坡中的含水量，减少基质吸力，并削弱土体的抗剪强度。长期降雨会使水分在斜坡内部孔隙流动，从而加剧斜坡滑动趋势，造成失稳。降雨引起的山体失稳是地质灾害的主要原因，往往造成重大人员伤亡、财产损失以及公路和铁路交通中断。因此，降雨引起的滑坡问题亟需进一步研究[1-2]。

降雨入渗是指落到地表的雨水，通过土壤中的孔隙和空隙，自非饱和带流入饱和带，而补给地下水的复杂动态变化过程。因此掌握雨水在非饱和土种的渗流规律，是探究降雨条件下老滑坡复活机理的关键。传统的Green-Ampt 雨水入渗模型主要分析的是土体饱和入渗过程的入渗情况，其物理模型简单明了[3]。XIAO 等[4]基于非饱和土理论和渗流基本理论，进一步介绍了多孔介质饱和-非饱和、稳定-非稳定渗流微分方程，并且考虑了非饱和土的抗剪强度，采用一般极限平衡分析方法，针对饱和-非饱和边坡的稳定性进行了分析。LIU等[5]在饱和入渗原理和Green-Ampt 模型的基础上，探讨了在边坡表面恒定含水量和孔隙水压力随深度变化的非饱和入渗模型，通过对边坡初始含水率变化的分析，得到了入渗参数受到初始含水率、湿润锋饱和度、土体黏聚力和降雨强度影响的结论。

将有限元用于降雨入渗过程中边坡土体的渗流场和应力场的求解，所得的渗流过程中有效应力和孔隙水压力分布与简化的极限平衡法相比不仅更符合实际情况，而且能够详细描述边坡土体的整个渐进破坏过程[6]。HUANG 等[7]基于连续两相渗流方程和达西定律，同时考虑Buckley-Leverett 方程，构建了岩土介质饱和-非饱和渗流的数学模型，运用有限差分动力学方法将方程进行离散化，进而编制了新的三维程序，通过新模型模拟了降雨条件下边坡的渗流过程，揭示了边坡孔隙压力和饱和度的变化规律。杨国强等[8]从降雨入渗渗流理论出发，采用Geostudio 有限元软件，对比分析了非饱和土边坡在降雨等级与不同雨型下，对孔隙水压力及安全系数的影响规律。蒋中明等[9]在深入研究FLAC3D软件渗透分析模块功能和算法的基础上，通过编写FISH 函数，对FLAC3D 非饱和渗透计算功能进行了改进。同时在分析降雨入渗机理的基础上，编制了降雨入渗和边界出渗的FISH 函数，并对边坡三维降雨入渗过程进行了模拟。

以上研究都是基于非饱和土渗流理论开展相关的降雨边坡失稳问题和水-力耦合分析，但对不同降雨强度条件下老滑坡的应力应变耦合以及现实数据对比仍需进一步解释。二庄科滑坡是一处位于陕北的老滑坡[10]，本文依托实际工程地质水文背景，在了解饱和和非饱和渗透理论的基础上，结合对FLAC3D 软件渗流分析模块的解析，利用FISH 语言的二次开发，编写了降雨入渗边界处理函数和非饱和区渗透系数实时更新函数，模拟降雨条件下老滑坡的饱和和非饱和渗透过程。同时，从应力位移角度，探讨降雨强度对力场渗流场作用情况的影响，从而实现含水率（饱和度）-土压力（应力）-位移（应变）的耦合研究；进一步地将现场监测数据与FLAC3D 模拟结果进行对比分析，对上述计算结果逐项解耦考察，验证数值方法的合理性和可行性。依托本文数值手段，为后续工程现场数据提供了更多研究角度，包括揭示降雨条件下老滑坡复活规律与探究变形破坏过程，将实际观测数据与老滑坡整体变形情况建立联系，使基础监测结果立体智能化，保障从业人员获取更多信息，掌握降雨条件下老滑坡状况，从而及时做出决策。

1 计算方法

1.1 饱和非饱和渗流基本原理

多孔连续介质饱和非饱和渗流方程[11]如下：

式中：qi——单位流量向量/（m2·s-1）；

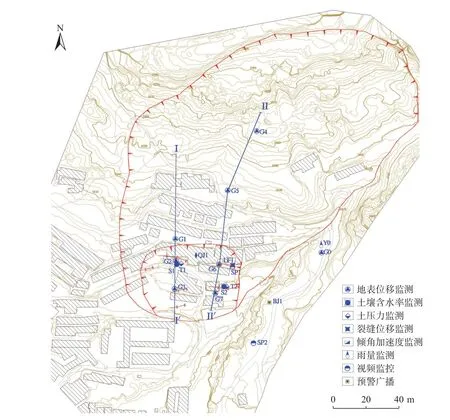
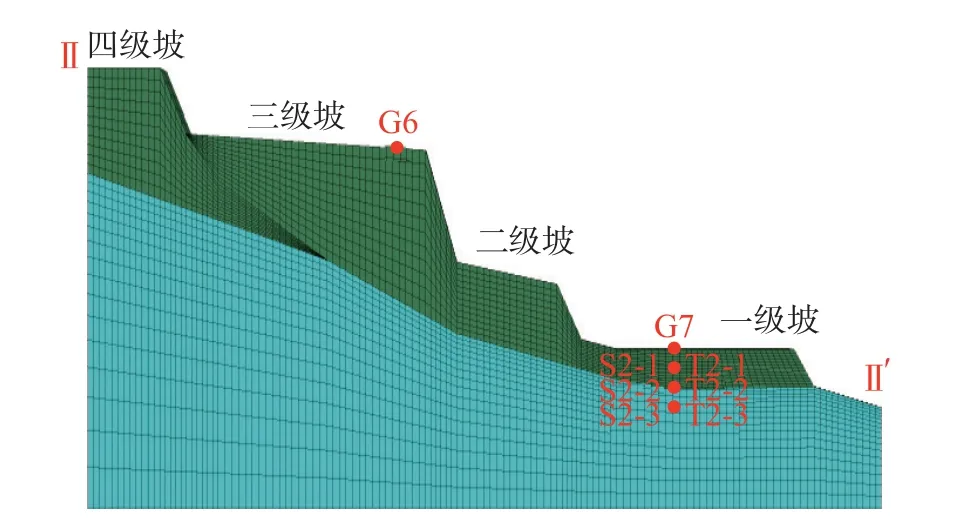
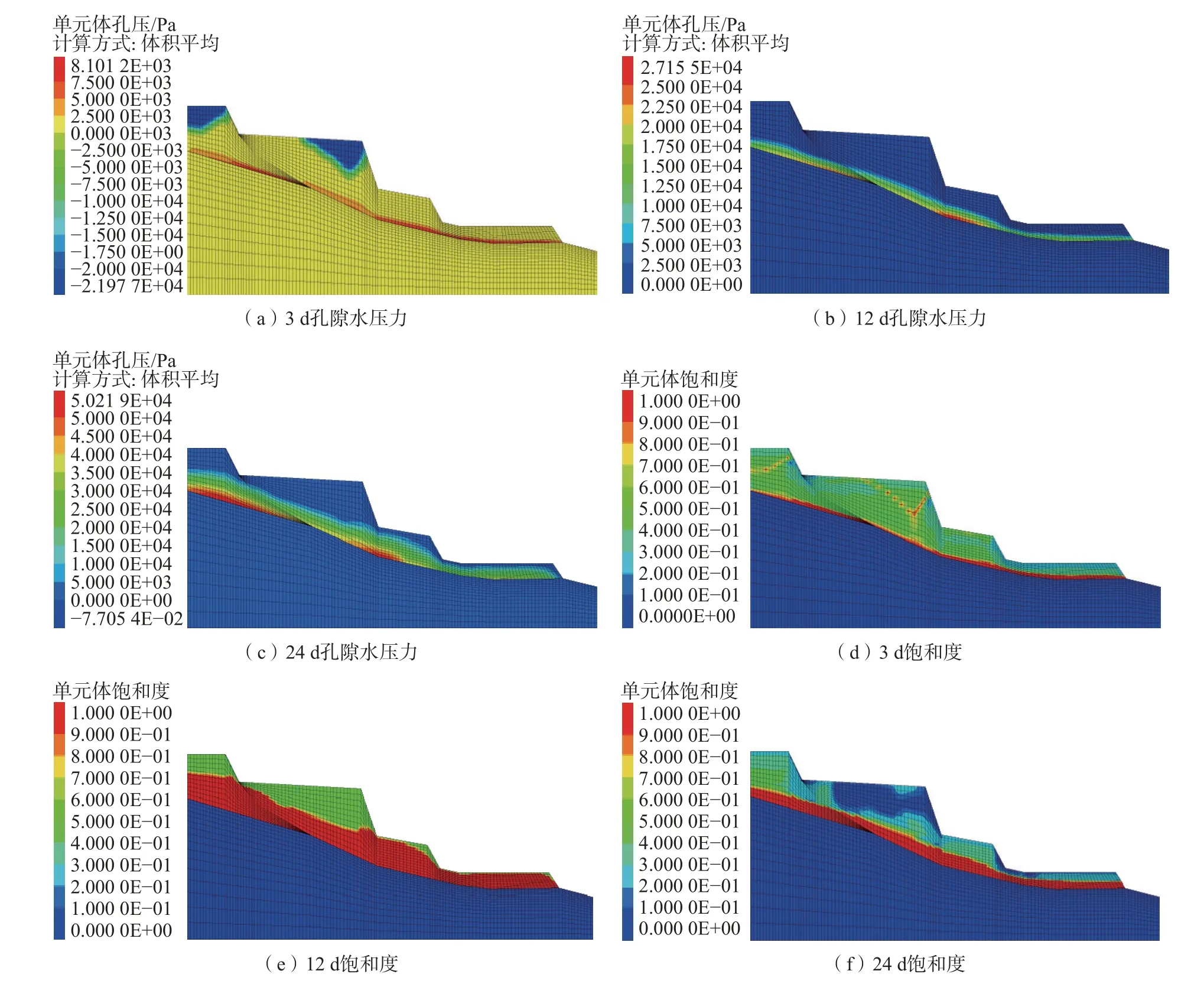
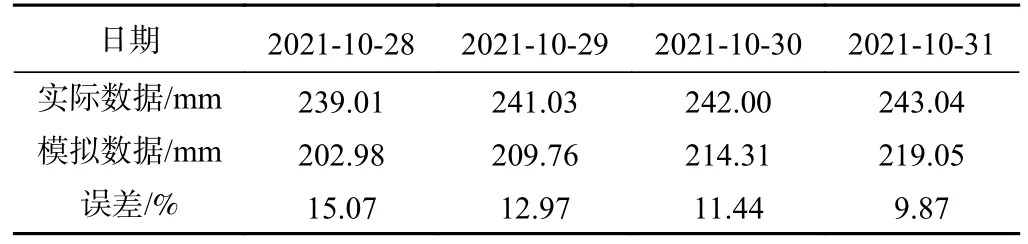
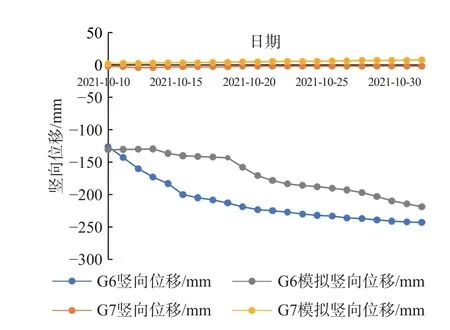
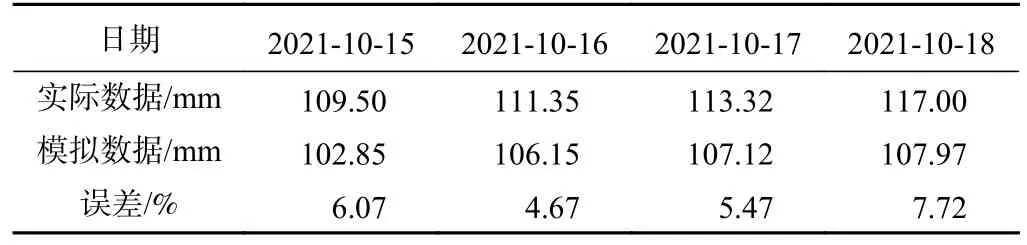
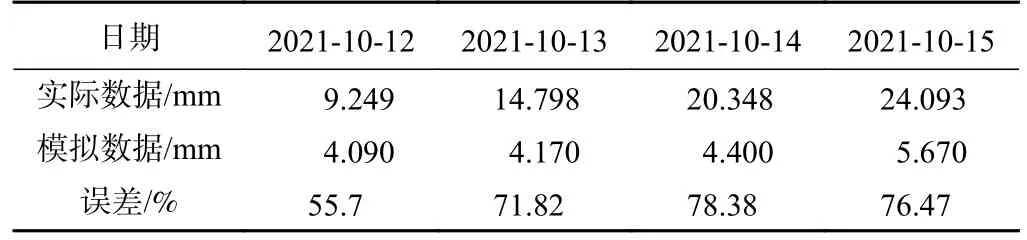
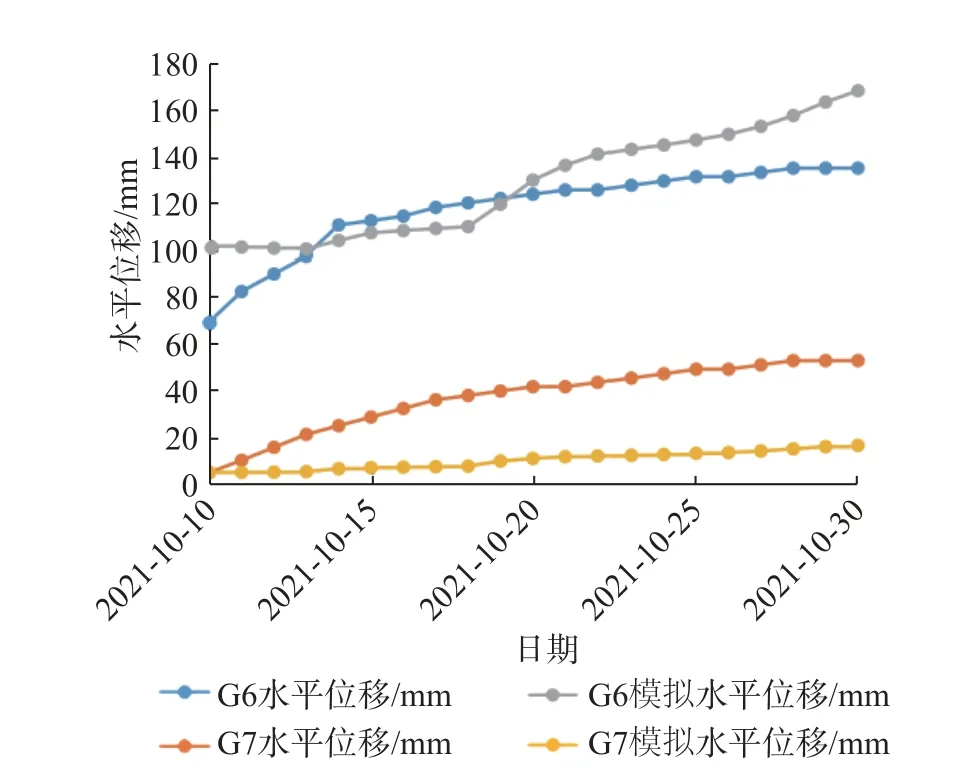
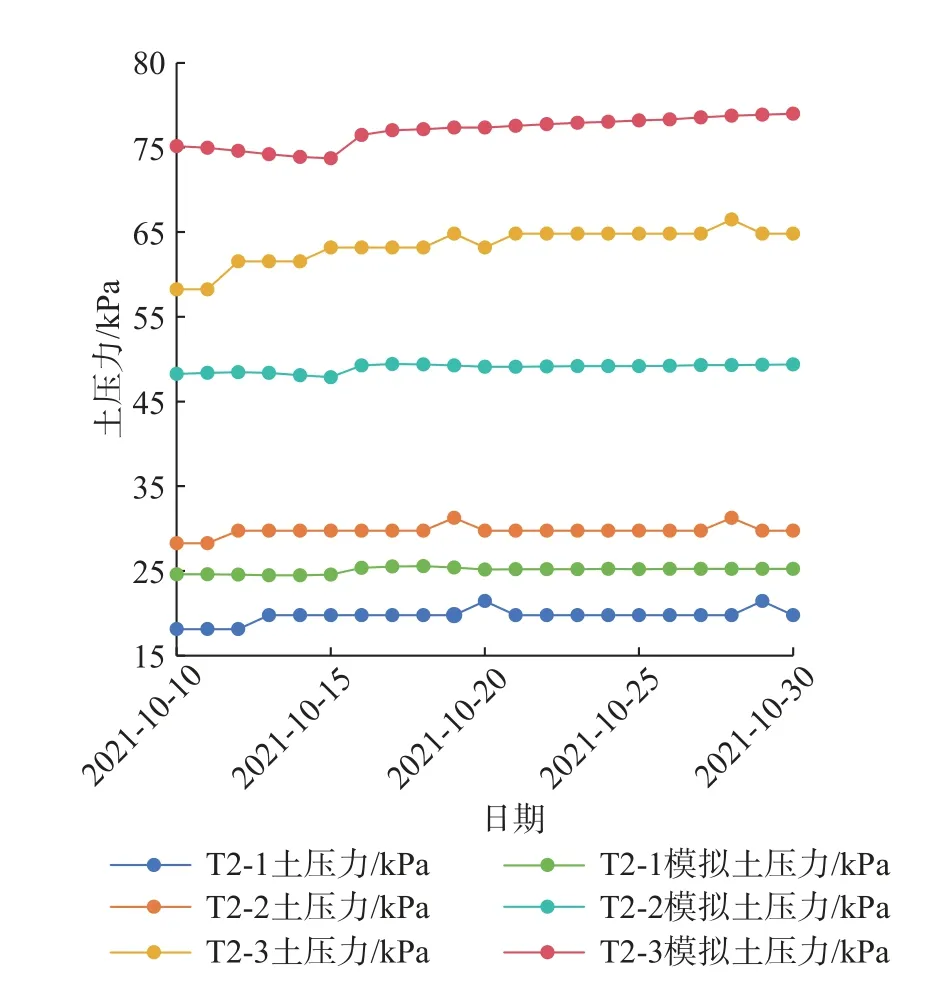
kr——与饱和度s相关的相对渗透系数，饱和区kr=1，非饱和区0

Kij——渗透系数张量/（m·s-1）；

h,j——水力梯度/m；

ψ——压力水头/m，ψ=p/γw，p为孔隙水压力/Pa，γw为水的重度/（kN·m-3）；

z——位置水头/m。

由式（1）可知，饱和渗流可以看成是饱和度为1.0时的非饱和渗流。非饱和渗流分析的关键在于非饱和区渗透系数依赖于饱和度变化而变化，同时，非饱和区的孔隙水压力可以表述为负值，也就是基质吸力。

1.2 FLAC3D 饱和非饱和渗流分析方法

负孔隙压力、饱和度与渗透系数三者相互关联[12-14]。随着降雨的进行，饱和度不断增加，基质吸力不断增大，同时渗透系数也会不断增加[15-16]。

在渗流计算过程中，流体压力、饱和度与流体体积改变量的关系式如下：

式中：M——比奥模量/Pa；

n——孔隙率；

t——时间/s；

p——流体压力/Pa；

s——饱和度；

ξ——流体扩散作用引起的单位体积多孔介质中流体体积改变量，当流体不可压缩时，其值等于单元流量改变量/m。

在进行饱和渗流计算情况下，FLAC3D 软件直接将节点上的饱和度（s）置为1.0，于是由式（2）得到下一计算时刻节点上孔隙水压力的更新计算公式为：

在进行非饱和渗流计算时，FLAC3D 将节点上孔隙水压力（μw）等于0，然后由式（2）得到计算节点饱和度的更新值为：

由此可见，FLAC3D 软件非饱和状态（饱和度）变化计算的主要依据是计算微元中流体体积改变量的变化值，而这与饱和度的定义相一致。

1.3 非饱和抗剪强度理论

在非饱和土与饱和土之间，强度差别的主要原因在于含水量引起广义结构强度的变化。非饱和土的强度一般可以表示为该土体处于饱和状态下的强度与基质吸力的附加强度（称为吸附强度）二者之和。

在非饱和土中，基质吸力也是非饱和土强度的重要参数，考虑基质吸力情况下的Mohr-Coulomb 公式：

式中：τ——抗剪强度/Pa；

c'——土体有限黏聚力/Pa；

ua——剪切面法向孔隙气压力/Pa；

uw——剪切面孔隙水压力/Pa；

(ua-uw)——土体剪切面上的基质吸力（其值与负孔隙压力绝对值基本相等）/Pa；

φ——土体有效内摩擦角/(°)；

φb——土体抗剪强度随着基质吸力（负孔隙水压力绝对值）增加的坡角/（°）；

σ——剪切面法向总有效应力/Pa；

ua——剪切面法向孔隙气压力/Pa；

(σ-ua)——土体剪切面上的法向应力净值/Pa。

2 工程概况及计算参数

2.1 工程概况

研究区二庄科滑坡位于延安市宝塔区，为一黄土基岩接触面滑坡，滑坡形态较清晰，轮廓明显，周界呈圈椅状（图1）。老滑坡宽310 m、长240 m、厚15 m，后缘发育有陡坎，高约20 m，滑体整体坡度30°左右。滑坡前缘经人工开挖扰动引起了次级滑动，次级滑坡发育有多组拉张裂缝，部分房屋发生变形，但次级滑坡暂未出现明显滑动[16]。

图1 二庄科滑坡全貌Fig.1 Overview of the Erzhuangke landslide

2.2 计算参数

根据现场调研以及查阅资料，确定模拟的老滑坡分为四级。最底部设置高度为0 m，一级边坡高度设置范围为0～14.4 m 的砂岩，土岩接触面处，局部岩石呈破碎状，坡度约为56°；二级坡高度设置范围是14.4～20.3 m，坡度约为61°；三级坡高度设置范围20.3～32 m，坡度约为69°；四级坡高度设置范围是32～40 m，坡度约为64°。其中二、三级坡为Qh 类型黄土，四级坡为Qp 类型黄土。模型参数设置见表1，采用摩尔-库伦（Mohr—Coulomb）模型。

表1 模型参数设置Table 1 Table of model parameter settings

2.3 模型和边界条件

为了验证模拟结果准确可行性，根据地质监测截面与境界设计剖面图确定尺寸数据，选择II 号断面建立几何计算模型（图2），为了进一步还原现场地质环境，几何模型设置为上下双层结构，上层计算模型为四级坡，一级坡高14.4 m，坡角56°；二级坡高5.9 m，坡角61°；三级坡高11.7 m，坡角69°；四级坡高8 m，坡角64°；下层设置为基岩隔水带，便于观测上层坡体孔隙水与饱和度变化情况。模型的有限元网格划分采用三角形和四边形，共13 896 个节点，6 720 个单元（图3），图中S2-1 为地下1 m 处含水率监测点S2；T2-1 为地下1 m 处土压力监测点T2，其他同理。

图2 工程地质灾害监测点分布图[10]Fig.2 Distribution map of engineering geological disaster monitoring points

图3 二庄科滑坡FLAC3D 建模Fig.3 FLAC3D modeling of the Erzhuangke landslide

模型边界条件：考虑实际情况，该横截面模型边界限制条件为顶部和斜边位置处不采取任何位移限制措施，为自由模式，其余边界部分限制边界垂直方向位移，同时滑坡设置为上线。此外下层基岩层渗透系数设置为恒定值0，在与上层滑坡接触面处形成为隔水层。

3 数值计算结果分析

基于上述理论方法与贴合工程背景所建立的几何模型，采用渗流应力耦合计算方法对边坡稳定性进行分析。选用FLAC3D 中的fluid 和mechanical 模块相互结合进行水-力耦合分析。同时利用FISH 语言，对边界渗流情况进行设定，并满足滑坡模型内部单元渗透系数实时更新，从而较为真实地模拟得到降雨条件下滑坡饱和非饱和渗透过程。同时根据上述渗流过程中坡体力场渗流场分布情况，从位移、土压力和饱和度的角度，与现场监测数据建立联系，形成方法验证关系。

3.1 降雨模拟方案

为了探求不同降雨情况下黄土滑坡复活规律，选取具有代表性的3 种情况进行研究，包括：小雨（3 mm/24 h）、暴雨（69 mm/24 h）和特大暴雨（250 mm/24 h）。研究时间范围为：降雨12 d，停雨12 d。同时建立空白对照组，对比分析在施加降雨条件后，滑坡内部剪应力分布与大小变化情况，进而解释在雨水渗流作用下滑坡复活机理。

针对不同降雨强度，迭代计算得到对应的渗流场和应力场，调取数据获得在降雨条件下，滑坡内部的孔隙水压力分布和土体饱和度随时间变化情况。从而进一步解释雨水非饱和渗流机理，分析其对土体强度折减与滑坡复活程度的影响。同时，通过滑坡内部应力与位移的关系，从宏观上对比不同降雨强度下，渗流场与应力场的耦合特点及其对滑坡复活的作用效果。

3.2 降雨条件下入渗时间对孔隙水压力及饱和度的影响

降雨过程中，非饱和区土体孔隙水压力发生剧烈变化，岩土体表层出现暂态饱和区。长期降雨情况下，滑坡土体孔隙水压力发生变化，为了探究滑坡降雨入渗机理，选取特大暴雨（250 mm/24 h）条件下滑坡三个时间点，包括：3 d，12 d 和24 d，分别对内部孔隙压力及饱和度的发展过程进行观测。

由图4 可知，在降雨强度为250 mm/24 h 情况下，降雨3 d 内，沿着既有裂缝，水分不断向下迁移，滑坡内出现部分孔压为零的连续滑动面，随着时间推移，该区域容易产生径流，导致土体抗剪强度大幅度降低，促使老滑坡复活，此时的降雨入渗深度约为2 m；在降雨12 d 时，在老滑坡与基岩接触面处，孔隙水压力转为正值，坡脚处首先产生了饱和区，雨水开始从底部聚集积累，饱和区逐渐由坡脚向坡顶开始扩展。这说明在特大暴雨（250 mm/24 h）情况下，降雨初期降雨影响范围变化的速度较大，随着降雨的不断进行以及深度的增加，降雨入渗的速率减缓，即入渗能力降低。坡面出现了地表径流，表层土体抗剪强度大幅降低，形成表层滑落，故孔隙水压力稍有降低。同时，在降雨观测过程中，坡脚处累计汇聚的雨水使得其成为整个坡面含水量最大的位置，抵抗外力的能力最弱。并且饱和带也随着降雨的进行逐渐从坡脚向坡顶发展。与此同时，即使降雨停止之后，由于蒸发作用，形成了新的负孔压区。

图4 特大暴雨情况下，孔隙压力及饱和度变化情况Fig.4 Variation of pore pressure and saturation under extreme heavy rainfall

3.3 耦合条件下降雨强度对滑坡复活程度的影响

在渗流应力耦合作用下，雨水渗流所产生的动水压力以体积力的形式作用于岩土体介质，使岩土体应力场发生改变，而岩土体又因应力变化发生压缩和膨胀，则其体积应变和孔隙率（比）也随之改变，将渗透特性反馈于渗流场。为了探讨水力耦合后对滑坡复活程度的影响，从应力和位移两个角度，研究降雨条件下坡体破坏规律。

3.3.1 应力

渗流场引起孔隙水压力变化，破坏了其原始应力平衡状态，引起有效应力变化。为了更加直观揭示出降雨改变渗流场，从而影响应力场的现象，将设置空白对照组（零降雨情况），与暴雨状况下的应力图进行对比。

图5（a）为切应力，相对于整个坡面，三级坡脚处切应力最大。根据非饱和土Mohr-Coulomb 强度理论，当切应力大于内部抗力时，滑坡会发生破坏因此坡脚处可能是最先破坏的地方。竖直方向应力受垂直方向土体高度影响较大，不同应力区域划分线与斜坡表面形状基本平行。图5（b）为降雨强度69 mm/24 h 情况下12 d 时切应力变化情况，由于降雨导致水的大量渗入，雨水在坡脚处汇集，导致此处含水率最大，并且在零降雨情况下，坡脚也受到整个坡面最大的剪切应力，雨水的重力和动水体积力加剧了坡脚的剪切力，故该处成为整个老滑坡较为危险的部位。同时，非饱和区体积含水率增加，导致负孔隙水压力减小，即基质吸力降低，微观上基质吸力对土体抗剪强度的贡献随之减少，导致了坡体的抗剪强度在很大程度上降低，从而产生剪切塑性屈服，使得老滑坡复活。

图5 切应力分布图Fig.5 Shear stress distribution map

3.3.2 位移

降雨强度与土体渗透系数是相互影响的。因此，在通过改变降雨强度来研究滑坡位移情况时，将雨水入渗过程考虑进去，得到的结果更为符合实际，进而反映不同降雨强度下滑坡的稳定性变化规律。

为了研究不同降雨强度条件下，滑坡位移场情况，在滑坡渗流应力场耦合的基础上，模拟了3 种降雨强度，根据滑坡范围对比雨水入渗作用情况，进而从位移场的角度探究降雨对滑坡稳定性的影响。

图6（a）—（c）分别为小雨（3 mm/24 h）、暴雨（69 mm/24 h）、特大暴雨（250 mm/24 h）情况下降雨24 d 滑坡形成时截图，可以看出随着降雨强度的增大，降雨形成的滑坡位移越来越大。由上述降雨入渗规律可知，孔隙水压力随降雨强度增大而上升速度加快，而由于大量雨水的汇入，导致负孔隙水压力减小，即基质吸力降低，滑坡整体抗剪强度减弱，使得最大位移随着降雨强度逐步增大，滑坡具有复活的可能性。同时因为雨水在坡脚处汇集积累，且该处受到最大剪切应力，使得其最先发生破坏，故最大位移也出现在坡脚处，从而产生剪切塑性屈服，滑坡开始复活。

图6 滑坡位移对比Fig.6 Comparison of landslide displacements

此外，滑移面位置含水量以及应力情况为滑坡形成的主要决定因素，不同强度降雨时间相同时，雨水入渗抵达的最大深度差距很小，而从坡面到湿润锋位置负孔隙压力变化随降雨强度增大而增大，即该范围内含水率随降雨强度增大而增大。从而使得坡体表层发生脱落。随着降雨的不断进行，坡体发生层层脱落乃至发生滑坡。

3.4 监测数据与模拟结果的对比

为了研究数值模拟结果是否贴合实际，从应力、应变、含水率三个角度，通过数值模拟与现场实际数据的对比结果，观测其吻合情况，进而论证数值方法的准确性与可行性。在对比分析位移土压力数据之前，首先选取监测预警地质断面两个测点G6、G7,位于一级三级坡地表浅层处，提取两处位移应力随时间变化情况，绘制成图表形式。

如图7 所示，图像分别显示了G6、G7 两个测点竖向位移对比情况。首先，G6 点实地测量的位移数据整体呈负向增长，且增长速率逐渐减小。其原因得出，G6 点位于三级坡中间地表浅层位置，在降雨初期，雨水入渗速率较快且范围广，形成的暂态饱和区在雨水渗流的情况下形成贯通径流，在滑坡内部形成软弱滑动裂隙，土体整体抗剪强度降低。且主要向滑坡坡脚处汇集，该处产生的饱和区形成塑性流动带，导致上级坡出现较大向下滑动的趋势，并且沿着坡脚方向出现局部破坏情况，故开始时向下产生的位移速率较大，表2 截取部分数据进行对比，结果显示这一阶段与模拟结果基本吻合，可以如实反映真实情况。反映到实际则是滑坡地表在降雨初期产生较大塌陷，而随着降雨的持续进行，坡体沿着圆弧滑裂带发生整体破坏，此时沉陷程度减弱，向下位移速率减缓，故涉及到位移部位增加，但位移距离减小。对于位于一级坡的G7 测点，其现场实测数据几乎保持不变，可能在降雨条件下局部产生湿陷现象而产生较小波动，究其原因可能是该级坡高度较低，降雨对其竖向沉降影响较小。由表3 可知，G7 对应的数值模拟点与实测结果趋势与位移大小基本保持一致，不过其中出现了部分正向位移，根据上述分析可知，在持续降雨条件下上级滑坡向下产生整体滑动，下级滑坡坡底受到来自上级滑坡沿着坡脚方向滑移的土料填充，因此，测点呈现出较小向上运移的现象。

表2 G6 点竖向位移实际模拟数据对比Table 2 Comparison of actual and simulated vertical displacements for monitoring point G6

表3 G7 点竖向位移实际模拟数据对比Table 3 Comparison of actual and simulated vertical displacements for monitoring point G7

图7 G6、G7 监测点在降雨过程中的竖向位移及模拟结果Fig.7 Vertical displacement and simulation results of monitoring points G6 and G7 during rainfall process

图8 展示的为G6、G7 测点水平位移的对比结果，基于上述讨论结果，在降雨初期，滑坡发生局部剪切破坏，上级坡处于变形剧烈期，具有向下滑动的趋势，产生容易产生较大位移，故G6 点曲线显示出较大斜率，而后期滑坡整体剪切破坏对水平位移做出主要贡献，位移增长斜率减缓。数值模拟曲线则展示出较为平稳的增长趋势，表4 显示中间时段模拟与现场数据对比情况，拟合结果与实际数据不断贴近，取得较好仿真效果。究其原因则是强度折减算法使得滑坡整体破坏连续存在，而由于水力耦合迭代计算作用，渗流场的持续增强破坏了土体抗剪强度，径流作用加强，影响不断扩大，测点位移迅速提高。而下级坡此时仅受部分少量上级饱和流塑土压力作用，由于降雨的持续，导致饱和区的不断累计，使得G7 点所在坡面达到某一临界点后被推移，使得其向坡脚处滑动，水平位移持续增加，表5 为临界点处模拟与实际数据对比结果。模拟曲线与G6 相似，整体上较为平滑，属于上层坡对下层土体堆积填充的过程，水平位移持续缓慢增加。但是表5 中G7 点水平位移模拟情况和竖向位移模拟情况类似，均存在趋势上与实测结果类似，但是误差上差异较G6 点大的情形。主要原因在于，FLAC3D 基于有限差分算法，土体材料基于连续性假设，按照土力学计算方法，滑动面前缘剪出在G7 点左方，这就导致模拟过程中G7 点所在的位置受上部土体推动力较小。进而导致G7 点的水平和竖向变形与实测值差距较大。

表4 G6 点水平位移实际模拟数据对比Table 4 Comparison of actual and simulated horizontal displacements for monitoring point G6

表5 G7 点水平位移实际模拟数据对比Table 5 Comparison of actual and simulated horizontal displacements for monitoring point G7

图8 G6、G7 监测点在降雨过程中的水平位移及模拟结果Fig.8 Horizontal displacement and simulation results of monitoring points G6 and G7 during rainfall process

图9 展示了G7 点位处的竖向深度3 个测点处的土压力值对比情况，T2-1、T2-2、T2-3 相互间隔1 m，并从地下1 m 处依次向深处延伸。由现场数据可以看出，三个位置竖向土压力均存在一个缓慢增长的过程，这是因为滑坡土体颗粒间存在天然孔隙，由于雨水的填充和润湿，增加了竖向土压力值，后续时段内数据基本保持平稳，此时土体内主要起到渗流连通作用。而数值模拟部分对应的三条曲线均高于现实情况，这是因为实际滑坡中土质复杂不均匀，存在重度较低的软弱松动土层，导致真实土压力较小。

图9 G7 监测点在降雨过程中的竖向土压力及模拟结果Fig.9 Vertical soil pressure and simulation results of monitoring point G7 during rainfall process

图10 显示了G7 点地下2 m 处实测数据与模拟结果的对比情况，S2-2 现场含水量保持在56%左右，且随时间基本稳定不变，说明该深度土体达到饱和状态，主要起到向下渗流雨水的作用。而模拟结果中降雨初期与中后期基本与实测数据吻合，保持平行不变，但当降雨进程达到12 d 时，含水量出现突变，由原来的48%左右骤上升到70%左右。该处可能在渗流场作用下，滑坡在此处发生局部复活，饱和土体被割裂，部分非饱和土体在渗流和整体变形作用下发生短期置换，随着时间的推进，滑坡复活逐渐整体结构化，故含水率在降雨中后期趋于稳定，与实际情况相符。

图10 G7 监测点深度2 m 处在降雨过程中的饱和度及模拟结果Fig.10 Saturation and simulation results at a depth of 2 m for monitoring point G7 during rainfall process

4 结论

（1）滑坡内部监测到部分暂态饱和区，即孔压为零的连续滑动面，随着时间推移，该区域容易产生径流，导致土体抗剪强度大幅度降低，造成滑坡复活。同时，在降雨观测过程中，坡脚处累计汇聚的雨水使得其成为整个坡面含水量最大的位置，抵抗外力的能力最弱。并且饱和带也随着降雨的进行逐渐从坡脚向坡顶发展。

（2）雨水的重力与和动水体积力改变了原有应力场，使得土体单元受到更大的剪切力，形成滑裂带。同时，由于雨水在坡脚处汇集，导致此处受到整个坡面最大的切应力，最大位移也发生在坡脚处，从而产生剪切塑性屈服，滑坡复活。

（3）负孔隙水压力减小导致基质吸力对土体抗剪强度的贡献随之减少，容易发生剪切破坏造成滑坡复活。同时，雨水在边坡孔隙中的不断渗透，导致暂态饱和区随着降雨的持续发展为了贯通径流，从而割裂了滑坡的整体性，因此极大促进滑坡复活的可能性。

（4）从位移应力和渗流饱和度的角度，发现数值结果与监测数据的误差较小，验证了模拟方法的可行性与合理性。此外，对于后续工程实际情况，可通过土压力、位移、饱和度三方面实测数据，判断降雨条件下滑坡复活的趋势，并对拟破坏程度预测。同时，可在此基础上建立预警系统，进而针对具体状况采取相应防护措施。

（5）由于FLAC3D 数值模拟方法本身的局限性，以及本文中采用的数据具有经验性、单一性和反演性，造成计算结果和实际结果具有一定偏差。因此，笔者将下一步的研究重点放在动态本构模型的选用、三维模型的开发和有限元-离散元联动耦合上，并提高土工实验的数量以提升数值模型的合理性。