智能化发展的共同富裕效应
--基于增长效率与分配公平的并存协同性研究
叶肖峰,王成军,李 雷
(浙江农林大学 经济管理学院,浙江杭州 311300)
共同富裕是社会主义的本质要求,是中国式现代化的重要特征。(1)见https://m.gmw.cn/baijia/2021-08/24/35105579.html。因此,党的十九届五中全会明确提出了到2035年“全体人民共同富裕取得更为明显的实质性进展”的目标。共同富裕有两个关键词,一是“富裕”,二是“共同”,这意味着不仅要把“蛋糕”做大,同时还要把“蛋糕”分好,即实现增长效率与分配公平二者并存。改革开放到21世纪初期,中国更注重做大“蛋糕”这一单一目标,虽然中国实际GDP总量以年平均约为9.36%的速率增长,但居民基尼系数从1978年的0.317,在2008年上涨至最高的0.491,至今仍是居高不下。[1]追求共同富裕就是要实现做大“蛋糕”和分好“蛋糕”相辅相成,[2]即实现增长效率与分配公平二者的协同。只有实现增长效率与分配公平二者的并存与协同,才能真正实现共同富裕。18世纪以来,经过三次工业革命的洗礼,科技取得了巨大进步,使得人类社会得到了飞跃式发展。如今,以智能化为标志的新一轮技术革命正在与社会经济各领域深度融合,成为重塑各国经济结构的重要推力,各国都在围绕发展智能化技术做出战略规划。我国“十四五”规划明确强调,要推动智能化技术向全部行业渗透融合,据相关数据显示,中国人工智能化产业的规模在2020年已经达到3 031亿元,约占全球比重的24.70%,(2)数据来源于中国信息通信研究院数据研究中心。预计到2030年,全球人工智能经济规模将达到15.7万亿美元,而其中的70%将由中美两国贡献。(3)数据来源于普华永道于2017年发表的“Sizing the price:What's the real value of AI for your business and how can you capitalize?”一文。因此,在推动经济快速发展过程中,研究中国智能化发展能否实现增长效率与分配公平的并存协同,对我国共同富裕战略目标的顺利实现具有重大的现实意义。
中国智能化发展能否实现增长效率与分配公平的并存协同?学者从智能化发展对增长效率和分配公平影响两个角度进行了初步的研究。一是认为智能化发展提升了增长效率,如:构建任务自动化模型定性分析可知,人工智能在特定条件下将会驱动经济爆发性增长;[3]利用国家层面的面板数据进行实证研究可知,人工智能所带来的自动化将会提高增长效率。[4]二是学者就智能化发展对分配公平的影响结论存在较大的分歧,如:文献[5]认为智能化发展不利于分配公平;文献[6]则认为,智能化发展将通过新工作创造效应和生产率效应促进中国的益贫式发展。
学者关于智能化发展对增长效率与分配公平的影响的研究主要侧重于智能化发展对增长效率或者分配公平的单方面探讨,缺乏在一个统一的逻辑框架下面进行的全面分析。增长效率会影响分配公平,分配公平又会反作用于增长效率,[7-8]而现有研究大都忽视了增长效率与分配公平二者的协同性。[9]
在理论层面,本文构建了一个具有最终产品的生产部门、城市和农村生产部门、专业化产品生产部门等四类生产部门以及创新研发部门的经济学模型,以一个统一的逻辑框架探讨智能化发展能否实现增长效率与分配公平的并存协同,为智能化发展助力共同富裕提供理论基础。在实证层面,本文从“投入→产出”视角刻画各省份智能化发展水平,并采用异质性视角下的全要素生产率衡量增长效率,通过联立方程模型,探讨在不同收入分配制度下智能化发展如何实现增长效率与分配公平的协同,为智能化发展助力共同富裕提供实践基础。
一、理论模型与分析
(一)模型构建
借鉴文献[10]的研究,本文将最终产品部门Y的生产函数设定如下:
(1)
其中,Yu和Yr分别代表城市生产部门和农村生产部门,ε∈[0,+∞)为两部门之间的替代弹性,γu和γr为两部门在总生产中的相对重要性。
借鉴文献[10]的研究,将城市和农村生产部门Yi的生产函数设定如下:
(2)
其中,Li表示部门i使用的劳动力;xi(j)为部门i使用的第j类专业化产品,其种类越多,代表生产水平越高,同时假定0<α<1;此外,中间产品xi的成本标准化为1-α;Ai为部门i的技术水平。
借鉴文献[11],将技术创新可能性前沿设定如下:
(3)

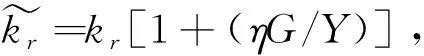
Au=exp(ruI)Ar=exp[(1+ητ)krI]
(4)
其中,ru表示城市技术随智能化发展I的进步速度,此外,ru>(1+ητ)kr恒成立。
由于中国政府部门所具有的泛利性,其效用与全社会的效用重合,[13]因此,将政府部门的效用设定如下:
U=growth×exp[-ζln(gap)]
(5)
其中,growth为增长效率,gap为收入差距,ζ=f(growth,gap)为政府对分配公平的偏好,即政府所实行的分配制度取决于增长效率与分配公平给政府部门带来的效用大小,满足∂ζ/∂growth>0以及∂ζ/∂gap>0,表明增长效率越低,收入差距越小,其越偏向于采取有利于增长效率的分配政策;而增长效率越高,收入差距越大,其越偏向于采取有利于分配公平的分配政策。如改革开放初期,收入差距小而经济发展落后,实行“效率优先”的分配政策;之后,经济不断发展而收入差距一直居高不下,分配政策开始逐渐重视公平。
(二)智能化发展对增长效率与分配公平的并存性分析
通过求解经济系统的均衡解,可得城市生产部门和农村生产部门收入差距和最终产品生产部门的增长效率如下:
(6)
growth=(1-τ)[n+A+BC(1+ητ)]/(1+ρ-ϑ)
(7)
其中,σ=εα-α+1为城市劳动力和农村劳动力的替代弹性,可以发现,只有当ε>1时,σ才会大于1。此外,为了保证系统的稳定性,借鉴文献[10-11]的研究施加一个外在条件:ρσ-ϑσ+1>0。观察式(5),可得结论如下:
结论1:Au/Ar随I的变化趋势为先增后减的“倒U型”趋势。故存在一点I*,使得Au/Ar达到最大,同时也使得min(ψTut,Aut)/min(ψTut,Aut)达到最大。而gap取决于σ与Au/Ar,当σ>1时,Au/Ar的增加将会使gap减少;当σ<1时,Au/Ar的增加反而将会改善gap。但根据相关文献对σ的计算,无论根据城市和农村所生产产品的替代弹性,还是根据城市和农村劳动力的替代弹性,均有σ>1,[14]故现阶段gap随I呈现先增后减的“倒U型”趋势或者上升趋势,这将取决于I*是否出现。若I*已经出现,则呈现“倒U型”趋势;反之,则呈现上升趋势。
其中,v=Lu/(Lu+Lr),A=ρvruI,B=ρ(1-v),C=krI。由于存在人力资本对技术进步的制约ρ和技术外溢ϑ,存在1+ρ-ϑ>0。观察式(6),可得结论如下:
结论2:∂growth/∂I>0,故最终产品生产部门的增长效率随着智能化的发展而提高;当政府部门只追求增长效率最大化时,即ζ=0,若满足η>1+(A+n)/BC,政府部门将收取τ*=(ηBC-n-A-BC)/2ηBC,反之,τ*=0。
(三)智能化发展对增长效率与分配公平的协同性分析
联立式(5)、式(6)以及式(7),求解出政府部门效用最大化下所收取的税率τ的大小,并对τ求ζ的偏导,可得:
(8)
其中,E=[n+A+BC(1+ητ)],D=[ρ(σ-1)]/(ρσ-ϑσ+1)。
结论3:由于(1-τ)ηCDE>0恒成立,易证,当τ>(η-1)/(2η)时,∂τ/∂ζ>0恒成立。
由结论2可知,当ζ=0时,τ*=(ηBC-n-A-BC)/2ηBC<(η-1)/(2η),此时不能保证∂τ/∂ζ>0恒成立。
不妨反证,当∂τ/∂ζ>0时,必定存在τ(ζ*)=(η-1)/(2η),故当ζ>ζ*时,∂τ/∂ζ>0恒成立,即政府部门对分配公平重视到一定程度时,∂τ/∂ζ>0恒成立。
又由于∂ζ/∂growth>0以及∂ζ/∂gap>0,可知:当政府部门对分配公平重视到一定程度时,存在∂τ/∂growth>0以及∂τ/∂gap>0,即增长效率与收入差距的提高均会促使政府部门收取τ**的税率,且τ**>τ*恒成立。
故根据结论1、结论2与上述分析可得,∂gap/∂growth<0以及growth/∂gap<0,即当政府部门对分配公平重视到一定程度时,增长效率的提高将会促进分配公平,分配公平的改善将会促进增长效率。
根据结论1、结论2以及结论3,可得:
∂gap/∂I=(∂gap/∂growth)(∂growth/∂I)+∂gap/∂I,
growth/∂I=(∂growth/∂gap)(∂gap/∂I)+∂growth/∂I。
即智能化发展对增长效率及分配公平存在直接与间接效应,因此,可得如下结论:
结论4:当ζ>ζ*且I>I*时,可得(∂gap/∂growth)(∂growth/∂I)<0且(∂growth/∂gap)(∂gap/∂I)>0,即智能化发展将会通过改善增长效率(分配公平)从而间接改善分配公平(增长效率),实现增长效率与分配公平的协同。
综上,本文提出两个假说:
假说1当智能化发展至一定程度时,将实现增长效率与分配公平的并存;
假说2当智能化发展至一定程度且对分配公平较为关注时,将实现增长效率与分配公平的协同。
二、实证策略与数据说明
(一)实证模型设定
本文采用面板数据双重固定效应模型检验研究假说1,即智能化发展对增长效率与分配公平并存性的影响,具体模型设定如下:
(9)
其中,i表示省份,t表示年份;被解释变量growth和gap分别表示增长效率以及分配公平,解释变量AI表示智能化发展水平;contrs表示控制变量;φi表示省份固定效应,φt表示年份固定效应;ε表示随机扰动项。
由于在使用单一方程估计法时会忽略各方程之间的联系,故本文采用面板数据联立方程模型的三阶最小二乘法检验假说2,即智能化发展对增长效率与分配公平协同性的影响,具体模型设定如下:
(10)
借鉴文献[15]的研究,将α1(β1和β2)定义为智能化发展对增长效率(分配公平)的直接效应,α2×β1与α2×β2(β3×α1)定义为智能化发展通过影响分配公平(增长效率)的间接效应。为了各系数之间能够对比分析,采用Z-score Normalization法对上述变量进行标准化处理。
(二)数据来源与变量设定
考虑数据的可获得性及排除重大事件对分配公平和增长效率关系的影响,(4)党的十九大在2017年10月召开,相关决议对分配公平和增长效率的关系做出了新的调整,在后文假说2的检验中,若单独采用2018年和2019年的数据进行分析,将会导致样本过少估计产生偏误;新冠疫情对经济造成了极大破坏,若采用2019年以后的宏观数据将会对实证结果产生严重的影响。本文采用2003-2017年30个省份的数据(除港澳台地区、西藏自治区外)作为研究样本,数据来源于《中国统计年鉴》《中国电子信息产业统计年鉴》《中国劳动统计年鉴》《中国人口和就业统计年鉴》《中国信息统计年鉴》《中国科技统计年鉴》《中国工业统计年鉴》《中国农村统计年鉴》以及各省份的统计年鉴等。
1.智能化发展水平
由于国内缺少直接测量智能化发展水平(AI)的统计数据,故对目前智能化发展的衡量较为缺失。在现有的研究中,有的文献采用以工业机器人的投入衡量智能化发展水平,也有的文献采用以人工智能为关键词的专利数量作为衡量智能化发展水平的测度。[16-17]智能化是建立在信息及智慧的发现、创造及应用基础上的,其充分发挥新一代信息技术的优化和集成作用,将互联网的创新成果深度融合于经济社会各领域,用单一指标不能完全衡量智能化发展程度。本文基于智能化发展的内涵,结合数据的可得性,并参考以往学者构建的指标体系,[3,18-19]从“投入→产出”视角刻画各省份智能化发展水平。智能化“投入”包括智能化创新、智能化基础和智能化支撑3个二级指标:智能化创新包括各省份软件企业个数以及软件人才数量;智能化基础包括各省份长途光缆密度以及电信固定资产投资;智能化支撑包括各省份R&D投入量、专利授权数。智能化“产出”包含智能化生活和智能化生产两个二级指标:智能化生活包括各省份互联网普及率以及移动电话普及率;智能化生产采用各省份工业机器人的使用数量衡量--由于缺少各省份工业机器人直接使用量数据,参照文献[3]中 “巴蒂克工具变量”的做法,假设各省份的工业机器人应用程度相同,通过各省份行业份额计算得到各省份工业机器人安装量权重,进而计算得出该省份的工业机器人投入数据。为了方便各指标之间的比较,本文采用线性无量纲法中的阈值法进行数据标准化。在权重处理上,采用熵值法对每个指标进行赋权,确定每个指标的权重后,采用线性加权的方法计算智能化发展指数。
2.增长效率
借鉴文献[20]的研究,将异质性视角下省际全要素生产率作为增长效率的衡量指标。在省际全要素生产率的测算上,相较于增长核算法和DEA方法,基于生产函数估算的SFA方法在采用了超越对数生产函数形式设定的模型后,能够检验该函数的有效性,从而保证较好的拟合效果。[21]因此,本文将采用SFA方法对省际全要素生产率进行测算,随机前沿生产函数设定如下:
lnYit=β0+β1lnELit+β2lnKit+β3t+1/2β4(lnELit)2+1/2β5(lnKit)2+1/2β6t2+
β7lnELitlnKit+β8tlnELit+β9tlnKit+vit+uit
(11)
其中,Yit为i省份t年的产出,本文以各省份的年生产总值表示产出,将2000年的生产总值作为不变量进行平减处理。ELit为i省份t年的有效劳动投入量,考虑到不同省份的劳动力人力资本水平存在差异,本文采用i省份t年劳动投入乘以该省份劳动力平均受教育年限与全国劳动力平均受教育年限的比值表示。此外,Kit为i省份t年的资本存量,考虑到资本结构的时间差异性,本文借鉴文献[22]的研究,将建筑、设备和其他费用的折旧率分别设定为8.12%、17.08%和12.1%,并通过加权得到全国分年份差异化的资本折旧率,然后应用永续存盘法计算资本存量。v为随机干扰项,u为技术无效率项,η为技术效率水平的时变参数。
3.分配公平
依据上文理论分析,借鉴文献[9]的研究,将城乡居民收入差距作为分配公平(gap)的反向指标,城乡居民收入差距越大,分配公平水平就越低。由于我国城乡居民收入差距主要体现在高收入与低收入的两端变化,而泰尔指数能够敏感地反映高收入人群和低收入人群的收入变动。[23]因此,本文采用泰尔指数作为城乡居民收入差距的衡量变量,计算公式如下:
(12)
其中I1和I2分别表示农村、城镇居民总收入,P1和P2分别表示农村、城镇总人口数,I=I1+I2,即I表示居民总收入,P=P1+P2,即P表示总人口数。
4.控制变量
为避免遗漏其他重要变量可能对估计结果产生的影响,本文在增长效率方程中设置控制变量:一是经济发展水平,以2000年为不变价格的各省份人均生产总值对数表示;二是城镇化水平,以城镇常住人口数除以总人口数表示;三是外商投资水平,以外商投资产值占总产值比重表示;四是经济开放度,以进出口贸易额占当年生产总值比表示;五是工业化水平,以第二产业增加值占当年生产总值比重表示;六是教育支出,以政府教育支出占财政总支出比重表示。此外,在分配公平方程中设置控制变量:经济发展水平、城镇化水平、经济开放度、教育支出、第一产业占比和第三产业占比,其中第一、第三产业占比以第一、第三产业增加值占当年生产总值比重表示,其余变量的设定与增长效率方程相同。
三、实证结果与分析
(一)智能化发展对增长效率与分配公平并存性的影响--假说1检验
1.基准回归结果
表1为智能化发展对增长效率与分配公平并存性的估计结果。第(1)至(2)列实证结果显示了智能化发展对增长效率的影响,智能化发展在1%的水平上均显著为正,表明智能化发展将促进增长效率的提高。第(4)至(5)列实证结果显示了智能化发展对分配公平的影响,智能化发展及其平方项均分别显著为正、负,表明智能化发展对收入差距存在“倒U型”的曲线关系。由上可知,当智能化发展至某一程度后,将同时促进增长效率与分配公平,即实现增长效率与分配公平的并存性。此外,本文基准模型可能存在双向因果、测量误差、遗漏变量等问题,使得估计结果存在一定的偏误。因此,借鉴文献[24-25]的研究,采用各省会城市至杭州的球面距离和当年浙江智能化发展水平的交互项以及各省份地形起伏度和周围省份智能化发展水平的平均值的交互项作为本文的工具变量,结果如第(3)列和第(6)列,与前文的基准回归结果一致,表明本文的估计结果较为稳健。
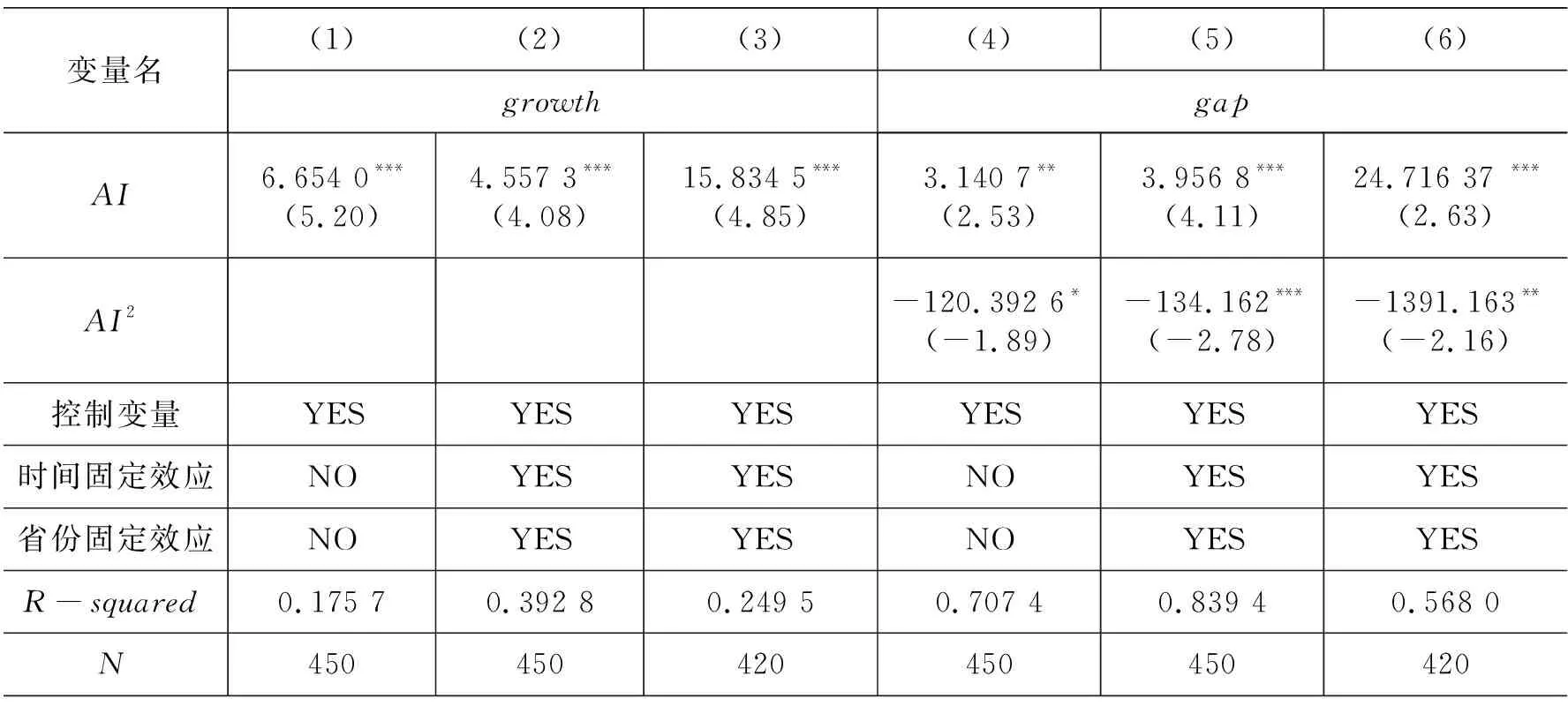
表1 智能化发展对增长效率与分配公平并存性的影响
2.影响机制检验
一是分析智能化发展对增长效率的影响机制。根据文献[20]的研究,将增长效率分解为规模效率SE、技术进步TP以及技术效率TE,用于智能化发展对增长效率的影响机制检验。表2为智能化发展对增长效率影响机制的实证结果。第(1)至(3)列为智能化发展对增长效率各组成部分的影响,结果均在1%的水平上显著为正,表明智能化发展将提高增长效率的各个组成部分,其中对规模效率(SE)的影响最大,技术进步(TP)次之,技术效率(TE)最小。其可能原因为智能化发展打破了原来时间和空间上的限制,使生产要素的流动与集聚变得更加容易,更容易产生规模效益。此外,为进一步探究智能化发展对规模效益中生产要素流动的影响,借鉴文献[26]的研究,将劳动力要素错配指数(LRA)和资本要素错配指数(CRA)用于生产要素配置效率的反向指标,其绝对值越大,表明生产要素配置无效率的程度越严重。第(4)、第(5)列为智能化发展对资本要素错配以及劳动力要素错配的影响,结果均在5%的水平上显著为负,表明智能化发展将改善劳动力要素和生产要素的配置效率,其原因在于智能化发展将突破原有空间和时间的限制,有效地解决信息不对称等问题,促进生产要素有效率地流动,还可以根据不同地区经济发展的禀赋,将生产要素进行智能匹配与重组,从而改善各地区生产要素的配置效率。
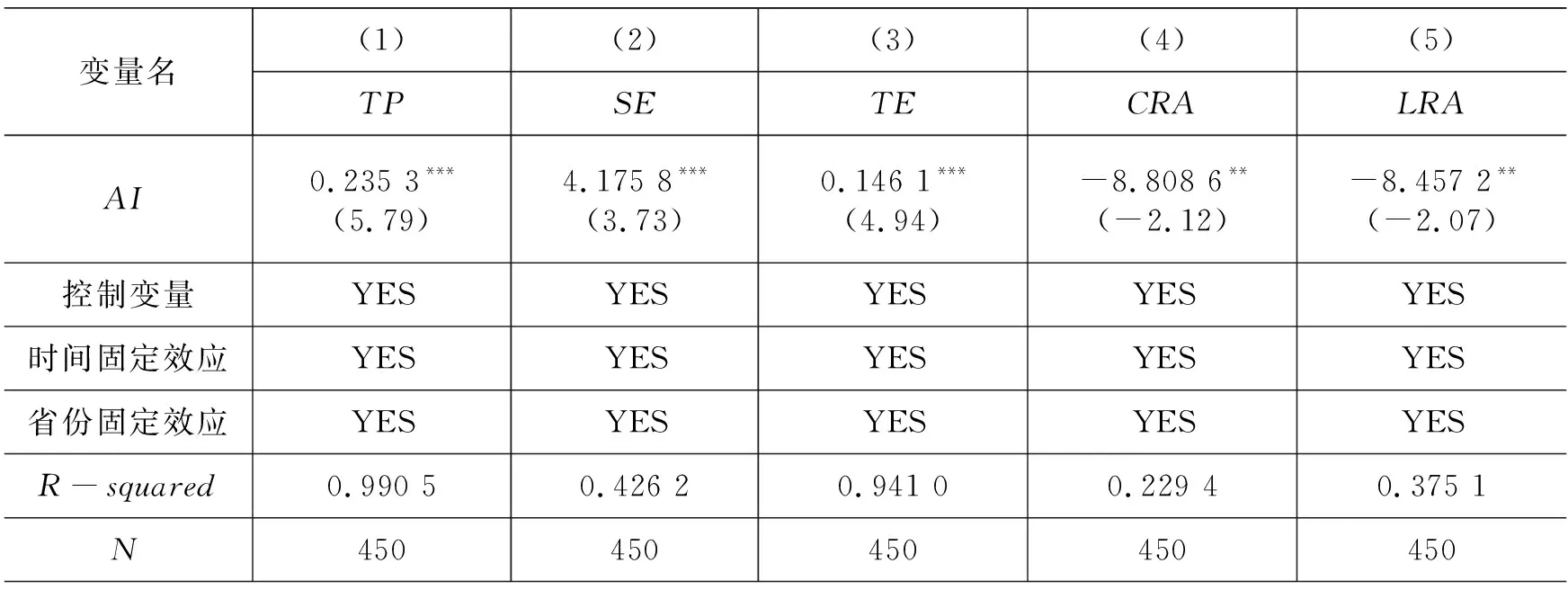
表2 增长效率影响机制检验
二是分析智能化发展对分配公平的影响机制。表3为智能化发展对分配公平影响机制的实证结果。本文将样本分为被称为“4G元年”的2013年前后,结果如第(1)至第(4)列显示,通过城乡之间横向对比,在两个时间段内智能化发展对城乡居民收入的影响均显著为正,但对城市居民的影响系数均大于农村居民。通过不同时期的纵向比较,智能化发展对城市居民收入的影响系数变小,对农村居民的影响系数却在变大。其可能原因有两点:其一,“4G”的出现加速了技术在城乡间的传播,使智能化发展变为“益贫式发展”,这也从侧面论证了收入差距随智能化的发展呈现“倒U型”的趋势;其二,“4G”的出现加快了智能化技术的更迭,使城市地区原有的人力资本水平逐渐不再适应,对城市居民的收入影响逐渐变小。
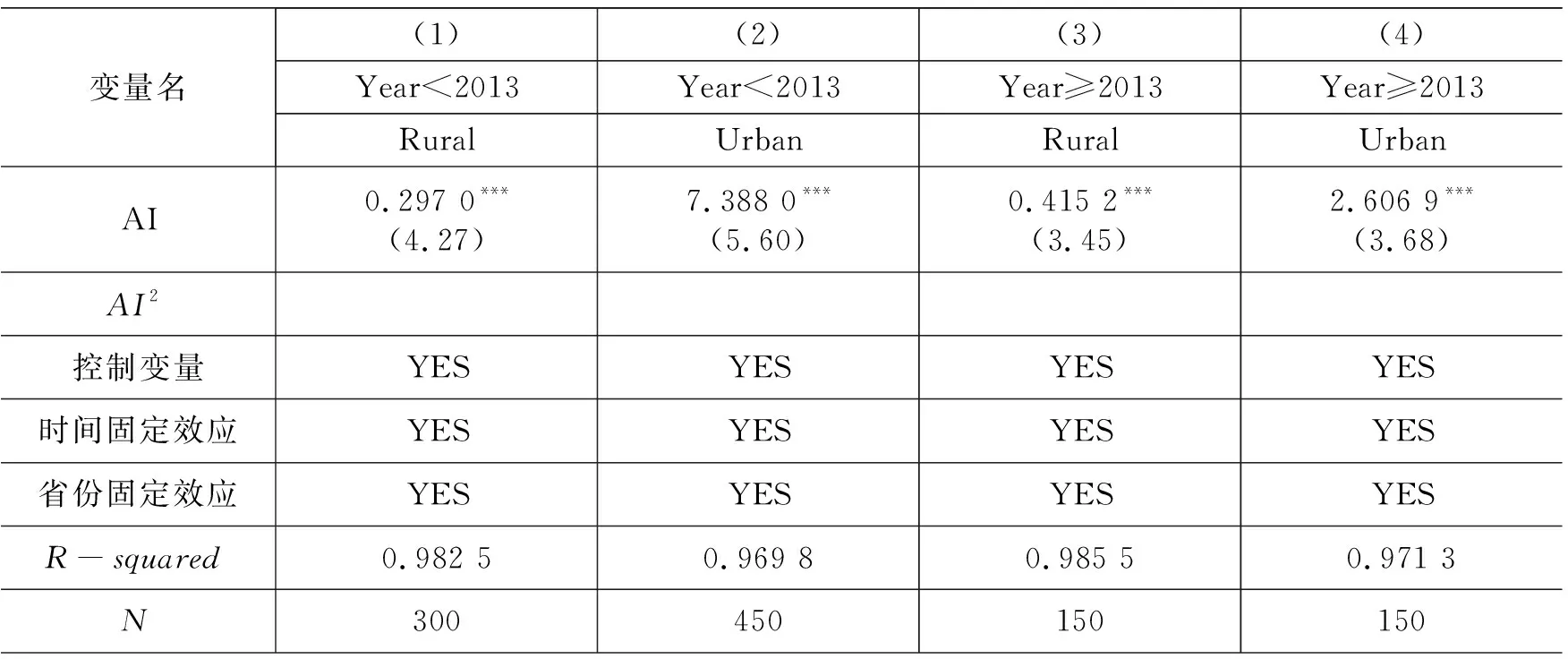
表3 分配公平影响机制检验
(二)智能化发展对增长效率与分配公平协同性的影响--假说2检验
根据文献[27-28]对中国收入分配制度演变的梳理,在本文的样本期内,中国收入分配制度的演变大致有3个重要时间点:第一,2002年,党的十六大报告提出“初次分配注重效率,再分配注重公平”,在一定程度上重新定义了效率与公平的边界,但发展理念仍是效率优先;第二,2007年,党的十七大报告提出“初次分配和再分配都要处理好效率和公平的关系,再分配更加注重公平”,政策逐渐改变为“效率优先,兼顾公平”的发展方针,开始重视分配公平;第三,2012年,党的十八大报告提出“初次分配和再分配都要兼顾效率和公平,再分配更加注重公平”,对效率与公平的关系又做了重大的调整,要实现效率与公平协调并重。本文将样本期划分为“效率优先”(2003-2007年)、“效率与公平逐渐兼顾”(2008-2012年)以及“效率与公平协调并重”(2013-2017年)3个时期,在3个时期内分配公平的关注度依次递增。
为验证本文所划分时期的准确性,借鉴文献[29]的研究,将增长效率以及分配公平与时间虚拟变量进行交互,并对其进行回归检验,实证结果如图1和图2所示。
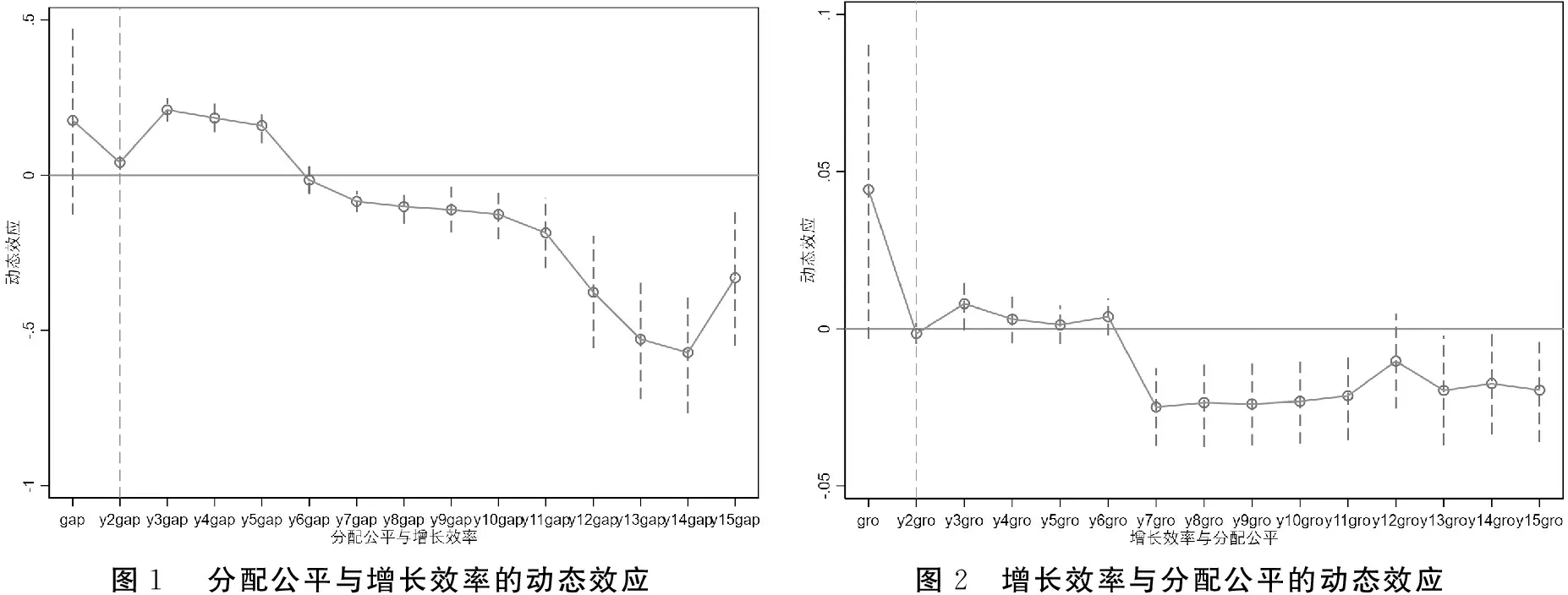
注:图1和图2中过原点竖线为相应估计参数的90%置信区间
图1和图2的实证结果显示,增长效率以及分配公平与时间虚拟变量均在2009年后开始显著为负,说明在2009年后,对分配公平的关注影响了分配公平和增长效率的相关关系。在党的十八大正式出台文件对效率与公平关系进行重大调整之前,可能就已经采取相应措施,故2009年至2011年可能为效率与公平的关系做出重大调整的过渡期。上述结果在一定程度上论证了本文所划分时期的准确性,为进一步验证上述结果,本文把样本期划分为2003-2008年以及2009-2017年两个时期进行稳健性检验。
1.基准回归
表4为智能化发展对增长效率与分配公平协同性的估计结果。第(1)、第(2)列的实证结果显示,在“效率优先”两个时期,分配公平对增长效率的系数显著为正,表明在这一时期,以牺牲一定程度的分配公平的方式来促进增长效率,此外,增长效率对分配公平的系数也显著为正,表明在这一时期,增长效率的提高在一定程度上降低了分配公平,即增长效率与分配公平之间并没有形成良好的相互作用。第(3)、第(4)列的实证结果显示,在“效率与公平逐渐兼顾”时期,增长效率对分配公平以及分配公平对增长效率的系数均为负,但不显著,表明在该时期,增长效率与分配公平开始逐渐形成良好的相互作用。第(5)、第(6)列的实证结果显示,在“效率与公平协调并重”时期,增长效率对分配公平以及分配公平对增长效率的系数均显著为负,表明增长效率对分配公平的影响是存在正面作用的。其次,经过计算可知,α2×β1<0且α2×β2>0,表明智能化发展通过影响分配公平从而改变增长效率的间接效应,呈现先减后增的“正U型”趋势,即智能化在前期将会通过降低分配公平抑制增长效率,但经过计算可知,α1+α2×β1>0,表明智能化发展在前期对增长效率的总效应仍为正,且当智能化发展跨过拐点后,将会通过改善分配公平这一间接效应与直接效应共同促进增长效率。此外,经计算得到β3×α1<0,表明智能化发展通过影响增长效率从而改变分配公平的间接效应,一直呈现改善分配公平的影响趋势,但由于β1+β3×α1仍大于0,表明在智能化发展前期,智能化发展通过提高增长效率从而改善分配公平这一间接效应尚不足以抵消智能化发展在前期降低分配公平这一直接效应,但由于-(β1+β3×α1)/(2β2)<-β1/(2β2),表明智能化发展通过影响增长效率从而改变分配公平这一间接效应,加快了拐点的到来,等跨过拐点后,智能化发展对分配公平的直接效应和间接效应都开始共同改善分配公平。
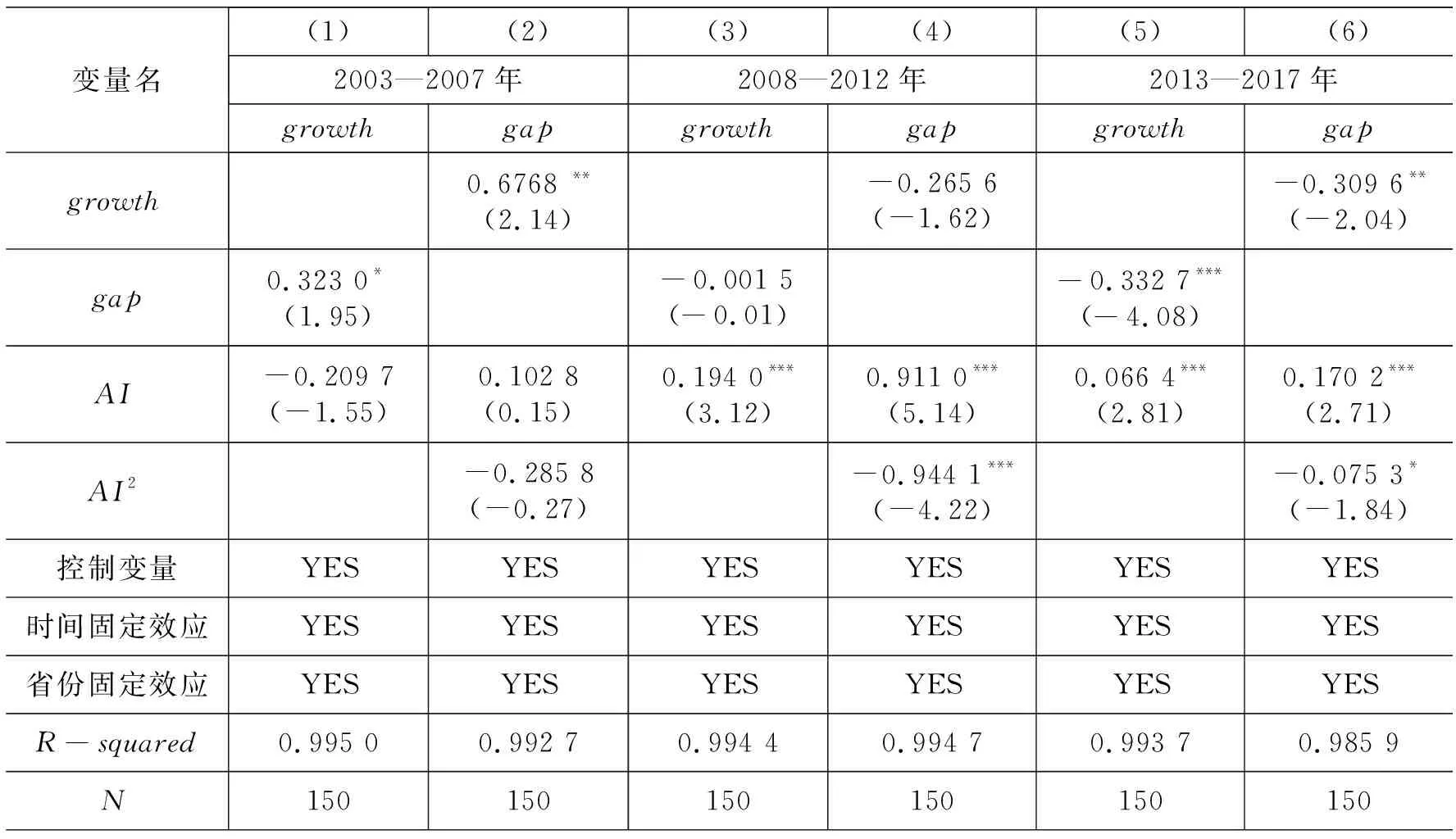
表4 智能化发展对增长效率与分配公平协同性的影响
因此,本文变量之间可以得到两条逻辑主线:第一条,智能化发展→增长效率→分配公平;第二条,智能化发展→分配公平→增长效率。将第一条和第二条的逻辑主线相连,可以合并成新的逻辑主线:智能化发展→增长效率↔分配公平←智能化发展。因此,从新的逻辑主线可知,智能化发展跨过拐点后,将成为实现文献[30]所说的以增长效率促进分配公平、以分配公平促进增长效率的重要推力,即实现增长效率与分配公平的协同性。
2.稳健性检验以及进一步分析
将样本期划分为2003-2008年、2009-2017年两个时期进行稳健性检验,并通过构造增长效率与分配公平影响智能化发展的计量方程,进一步解决智能化发展与增长效率及分配公平之间的内生性。实证结果如表5所示,与前文的基准回归结果基本一致,表明本文的基准回归估计结果较为可靠。
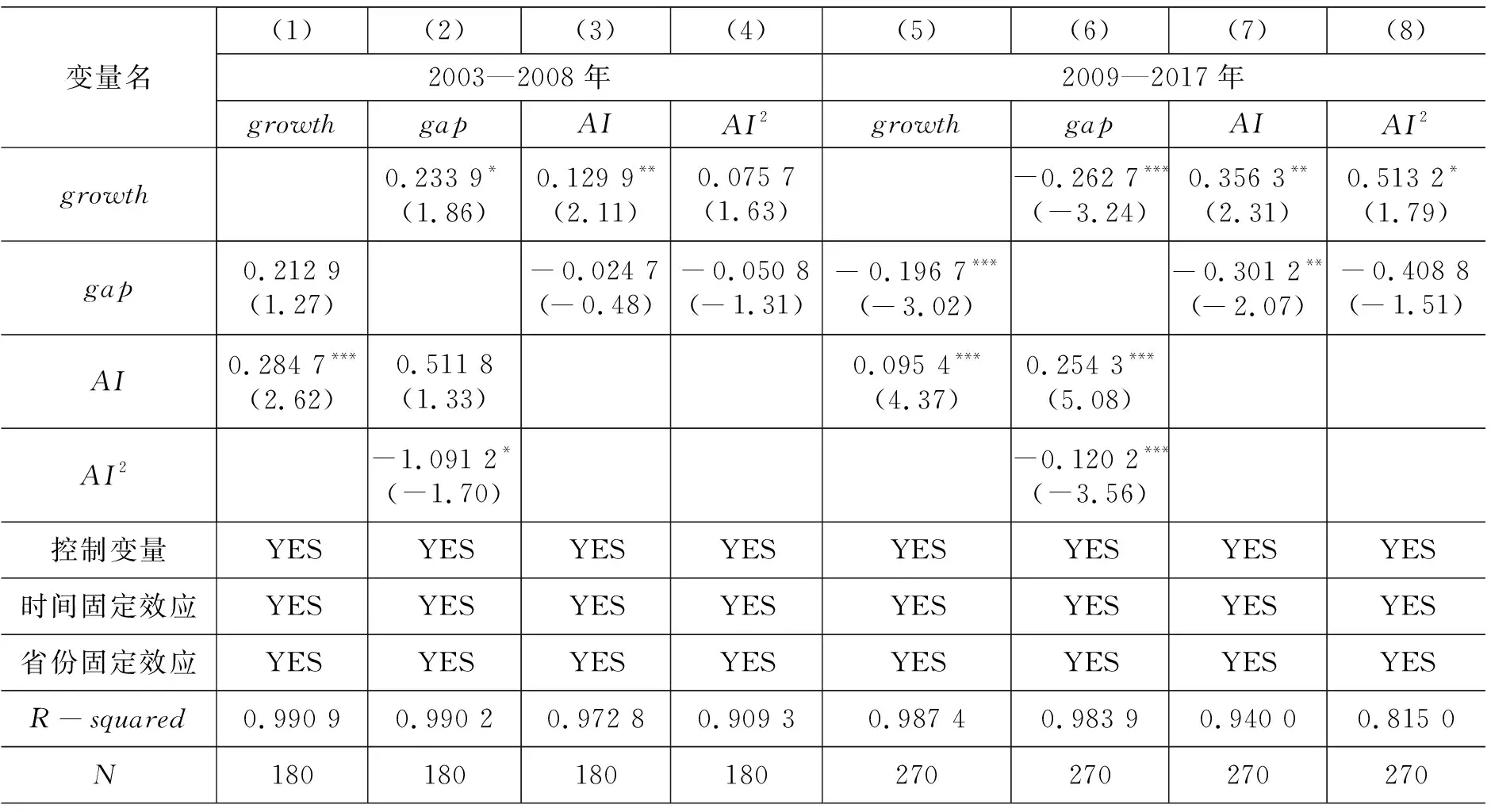
表5 稳健性检验
根据表5第(7)、第(8)列的实证结果,本文还可以得出两条新的逻辑主线:分配公平→智能化发展,增长效率→智能化发展。将这两条逻辑主线与上文逻辑主线相连,又可得出新一条逻辑主线:智能化发展↔增长效率↔分配公平↔智能化发展,即增长效率与分配公平的改善将会促进智能化发展,而智能化发展将会通过直接以及间接效应助力增长效率与分配公平的改善,故当智能化发展跨过拐点后,智能化发展、增长效率与分配公平三者之间将形成一个更大的良性循环模式。
四、结语
通过构建一个同时包括智能化发展、增长效率与分配公平的理论模型,对智能化发展进程中能否实现增长效率与分配公平的并存协同进行理论分析,提出相应的研究假说,并利用2003-2017年的省级面板数据,采用双向固定、联立方程等模型对研究假说进行了实证检验。第一,智能化发展对增长效率起到促进作用,而对分配公平起到先恶化后改善的作用。第二,在增长效率与分配公平协调并重的分配制度下,增长效率与分配公平将会形成良好的相互作用。因此,智能化发展将通过促进增长效率,以此促进分配公平,同时也通过促进分配公平,对增长效率产生先抑后扬的作用。
在智能化快速发展的背景下,应以包容性增长视角统筹协调增长效率与分配公平。第一,要做到“提速度”,即要加快推进智能化发展,促进分配公平拐点的到来。第二,稳步推进经济体制改革和经济结构调整,为实现增长效率与分配公平的“双赢”创造条件,从而实现以分配公平促进增长效率、以增长效率促进分配公平的良性“双循环”。第三,要做到“降高度”,由于在推进智能化发展的前期,会在一定程度上降低分配公平,所以要采取一定的措施使其拐点高度下降,如采用适当加大户籍制度改革力度以及加大农村基础设施建设力度的方式加以改进。

