基于最优路径的配电网弹性恢复力提升策略

张新宇,姚 方,文福拴,岳文全,薛栋烽

(1.山西大学电力与建筑学院,山西省 太原市 030013;2.长沙理工大学电气与信息工程学院,湖南省 长沙市 410114;3.浙江大学电气工程学院,浙江省 杭州市 310058)

0 引言

电力系统设计需满足安全、可靠、经济、环保4个基本要求,如今随着环境遭受破坏,极端灾害频发(如台风、冰灾等),输配电系统受到了严重挑战[1],因此电力系统应具备弹性[2],即抵抗小概率高破坏性的极端事件的能力;而对电力系统进行规划和设计,是提升弹性恢复力的必然要求[3-4]。

近年来,国内外学者针对电力系统弹性恢复力的提升[5-8]开展了大量研究。文献[9]把基于事件的校正调度(event based correction scheduling,ECS)模型和在线模型预测控制(online model predictive control,OMPC)模型用于微电网,集成定量弹性指标用到电力系统优化模型中,以增强系统弹性。文献[10]考虑极端天气的级联效应,建立系统组件的失效模型,通过加固输电线路来提高电力系统的弹性。文献[11]从城市电网长期规划、灾前预防2个角度,提升了电气化交通系统城市电网的弹性。文献[12]通过对配电网进行规划,并确定地下加固线路,考虑经济成本并最大限度地减少甩负荷,通过建立两阶段鲁棒优化(robust optimization,RO)模型,比较4种场景下的经济效益来验证所提模型对系统弹性提升的有效性。文献[13]在极端事件发生前规划,以积极主动的调度策略应对台风急剧变化的时空特征和组件变化状态,避免大范围级联性故障,提升系统弹性。文献[14]基于态势感知找出配电系统的关键节点,量化各节点设备对系统弹性的影响,并在关键节点配置备用电源提高系统弹性。文献[15]重点关注配电网,定义了与弹性相关的其他关键量(如阻力和脆性),提出了一个系统测量和评估电网弹性的框架,并评估最佳电力基础设施部署和运营计划的效果。

上述研究均属于事前预防策略,通过增加系统的冗余性去提升配电网弹性,加固线路花费高,而且存在以下问题:极端灾害发生具有不确定性,无法获取准确的线路加固信息。因此,制定故障发生后配电网恢复力的提升策略尤为重要。

文献[16]考虑电力部门和天然气部门之间的能源互助,提出了包含畸变率和线性包效应新度量标准的山谷型弹性模型,用于提升系统在极端天气下的性能。文献[17]考虑多种能源供应系统(如电力、天然气、氢气)的弹性恢复力提升,得出多个能源供应系统可提高电力系统弹性的结论。考虑到灾害发生后的级联效应,文献[18]根据可再生能源的波动性特点和级联故障原理,考虑灾害发生后通过孤岛划分由可再生能源供电。文献[19]提出了自适应孤岛算法,减小极端天气的级联效应,超出了传统抵御极端恶劣天气的措施,有效提升了配电网弹性。文献[15-16]利用各种弹性资源或网络重构等方法实现配电网的暂时功能恢复,时间尺度较短。除以上短时间尺度的恢复力提升策略外,文献[17-19]还考虑了时间尺度更长的电力基础设施恢复策略。此外,文献[18]提出将马尔科夫链用于表示电网的状态转换,证明了孤岛和配电网重构的微电网可有效提高电网在极端天气事件下的弹性。

上述研究对极端灾害不确定性、灾后配电网重建等研究仍然不足,忽略了极端自然灾害下交通网状态对灾后恢复和重建速度的影响。基于此,本文提出不同时间尺度的两阶段电力系统弹性恢复力提升策略。

1 面向配电网弹性恢复力提升的两阶段优化策略

本文研究分2个阶段:第1阶段为灾害发生伊始,通过联络开关和分布式电源(distributed generation,DG)进行网络重构,暂时恢复配电网供电能力,考虑燃气机组与联络开关的安装位置,对配电网进行孤岛划分和系统重构,以安装和配置成本最小为目标对机组配置数量与位置进行规划[20-21];第2阶段为在极端灾害发生较长时间后尽快维修以最小化负荷削减成本,从而提升配电网弹性。检修小组根据得到的元件故障信息,提前到达预设的故障维修初始点,从该点开展故障修复工作,考虑交通情况对检修路程时间的影响,在最短时间内完成检修,最小化该段时间的弃负荷量及系统损失成本。本文所建模型对两阶段模型进行协同优化,将灾时灾后两阶段作为整体,提出多时间尺度下的两阶段RO 模型,以制定最优的配电网弹性恢复力提升策略。

2 模型建立

2.1 燃气机组出力

接入配电网的电源为不受灾害影响可黑启动的燃气机组,其出力约束如下:

式中:Pg,t和Pg,t-1分别为机组在t及t-1时段的有功出力,Pg,max为其出力上线;Qg,t为机组在t时段的无功出力,Qg,max为其出力上线;α为机组的最大爬坡系数。

功率因数应满足

2.2 检修人员调度

检修人员调度本质上为一个车辆路径优化问题。检修小组从预设的初始故障点出发,根据极端自然灾害发生后检修中心分配的检修任务,对发生故障的元件进行维修。该问题使配电网恢复可靠供电尽可能快。

在电网-交通网融合系统中,检修人员的调度情况由其到达时间和维修时间共同决定,受到实时路况、突发事件影响,将这些影响用交通网络拥堵程度曲线来刻画,具有时空耦合特性。

检修小组在节点i与j间的通行时间为Tij,t,维修时间为T0,建立检修路程与时间的时空模型,如图1所示。

图1 检修小组路径Fig.1 Path of inspection team

为保证极端天气发生后检修小组能顺利通行,本文考虑了对交通运行的影响,节点i与j间的通行时间Tij,t、等效通行距离Dij,t及实际车速vi,t分别为

式中:Dij,0为节点i与j间的直线距离;vi,0为不受极端自然灾害影响下的理想车速;β为融合系数,表示极端自然灾害对交通流量的影响程度,可根据交通道路受灾严重程度来刻画。检修小组在极端灾害发生后,以最短时间从节点i到达节点j,对损坏的系统部件进行维修。若系统存在多个故障元件,检修小组需维修每个故障元件,从节点j出来后迅速到达下一个故障点,因此有必要选择一个最优抵达路径,确保配电网可靠稳定地恢复供电。

2.3 配电网运行约束

(1) 功率平衡约束。

式中:PL、QL分别为节点所接的有功和无功负荷;Pexc、Qexc为节点与节点之间的有功和无功交互功率,流入取负,流出取正。

(2) 节点电压约束。

式中:Ui,t、Uj,t为节点i及j在t时刻的电压幅值,Umax和Umin分别为其上下限;为支路i-j的阻抗;M为足够大的正数;aij,t为支路的连接状态,连接取1,否则取0;Sij,t为支路i-j在t时刻的复功率。

(3) 传输功率约束。

式中:Pij,t、Qij,t为支路i-j在t时刻流过的有功和无功功率;Pl,max和Ql,max分别为线路传输的有功和无功功率上限。

(4) 弃负荷约束。

仅考虑有功负荷衰减,约束如下:

2.4 配电网重构约束

设配电网所有节点组成的集合为Sb,将接入变电站、DG的节点和故障线路的首末节点构成潜在根节点集Sr。灾害发生伊始,通过联络开关和DG进行网络重构,暂时恢复配电网供电能力,尽量降低配电网的弃负荷量和投资成本。该过程中需满足以下条件:在配电网划分为孤岛供电系统中,断开的线路数目γj,t应该与孤岛个数一致,等于系统节点数Nb减去闭合线路数目,且各孤岛内各条线路处于闭合状态。约束条件如下:

式中Vij,t和Vjk,t分别为t时刻流经支路i-j及j-k的虚拟潮流。

3 面向弹性提升的RO 模型

配电网在极端天气条件下,量化各节点设备对系统弹性的影响,并在关键节点配置备用电源提高系统弹性,提出多目标优化模型,确定燃气机组的位置和容量,将系统弹性的优化转为经济成本优化。建立两阶段RO 模型,综合考虑电力系统的弹性恢复力提升。

为寻求最恶劣条件下故障修复时间达到最短,建立如下模型:

式中:τr,d为检修小组d修复故障线路元件r所需的时间;D为检修小组数量;Rd为故障元件集合。第1阶段决策向量为X,目标为系统硬件强化,以最小化配置成本;第2阶段决策向量为Y,目标是最小化弃负荷量和不确定变量,为寻求最恶劣路径下故障元件恢复速度最快。

考虑弃负荷量和配置联络开关数量,建立如下二者成本最小的约束模型:

式中:c1为单位弃负荷成本;c2为联络开关单位投资成本;Stie为线路集合;T为运行总时长。

式(9)(10)分别刻画了检修路程时间不确定性模型和配电网短时重构优化模型,2个模型可通过建立故障元件状态和修复状态之间的耦合关系,即综合模型,来联立求解:

式中c3为故障修复单位时间成本。

将该模型分解为主问题(master problem,MP)与子问题(subproblem,SP),进行反复迭代得到最优解。MP求最小值部分且松弛了部分约束,因此为最优值提供下界;SP求最大值部分,为原问题提供一个可行解,可作为最优解的上界。MP与SP不断更新、收敛最终得到最优解。

MP形式如下:

式中:q、b和g为常数矩阵;A、B、C和E为常系数矩阵;η为辅助变量;为第l次迭代最恶劣场景下维修所需的时间;Yl为第l次迭代添加至MP的辅助矩阵;K为最大迭代次数。

SP形式如下:

式中X*为MP的最优解。

根据对偶理论将SP式(13)转化为如下单层优化问题:

式中:umax为场景最恶劣值;umin为场景最佳值。

该双线性项可转化为

引入与E同维度的变量矩阵H(m×n维),采用大M法进行线性化[14]:

式中:M为足够大的正数组成的矩阵;I为单位矩阵。

通过列与约束生成(column-and-constraint generation,C&CG)算法进行MP、SP迭代求解,算法流程如图2所示。

图2 C&CG算法流程图Fig.2 Flowchart of C&CG algorithm

4 算例分析

4.1 基础数据

本文采用图3所示改进的IEEE 33节点系统进行仿真验证,3个DG 分别位于节点13、23、30。由于故障初始时刻,检修小组来不及及时维修,采取DG和联络开关进行网络重构,目标是使该时段弃负荷量达到最小,联络开关分布于图中虚线位置,连接着4对节点。节点1由于有充足的无功电源,电压保持恒定,其余各点电压偏差不超过±10%。接入各节点的负荷参数参见文献[5];根据文献[8]设置极端天气条件下受灾线路的维修时间,图示受灾线路2-3、5-6、8-9、14-15、26-27、30-31分别用数字1—6进行编号,具体如表1所示。

表1 元件修复所需时间Table 1 Time required for repairing components

图3 改进的IEEE 33节点系统Fig.3 Improved IEEE 33-node system

4.2 模型分析

假设配电网在11:00发生故障,图3所示受灾线路处于断开状态,以发生故障时间点为初始时刻,以0.5h为仿真时间步长,在Matlab平台调用CPLEX求解器进行求解计算。为验证两阶段RO显著提升配电网抵御极端天气事件的弹性能力,设置以下不同场景,如表2所示。计算各场景下的成本如表3所示,总成本为联络开关与DG 配置成本及弃负荷成本之和。表4为场景3、4下检修小组的检修路径。图4是根据灾害发生时车流量建立的模型,表示灾害到来后各时刻交通网的拥堵程度。图5为模拟所得的从灾害发生时到1天结束后场景3、4下的三相弃负荷功率。图6为DG在各时刻的有功出力。

表2 4种不同场景Table 2 Four different scenarios

表3 不同场景计算结果比较Table 3 Comparison of calculation results in different scenarios

表4 检修小组检修路径Table 4 Maintenance paths of maintenance teams

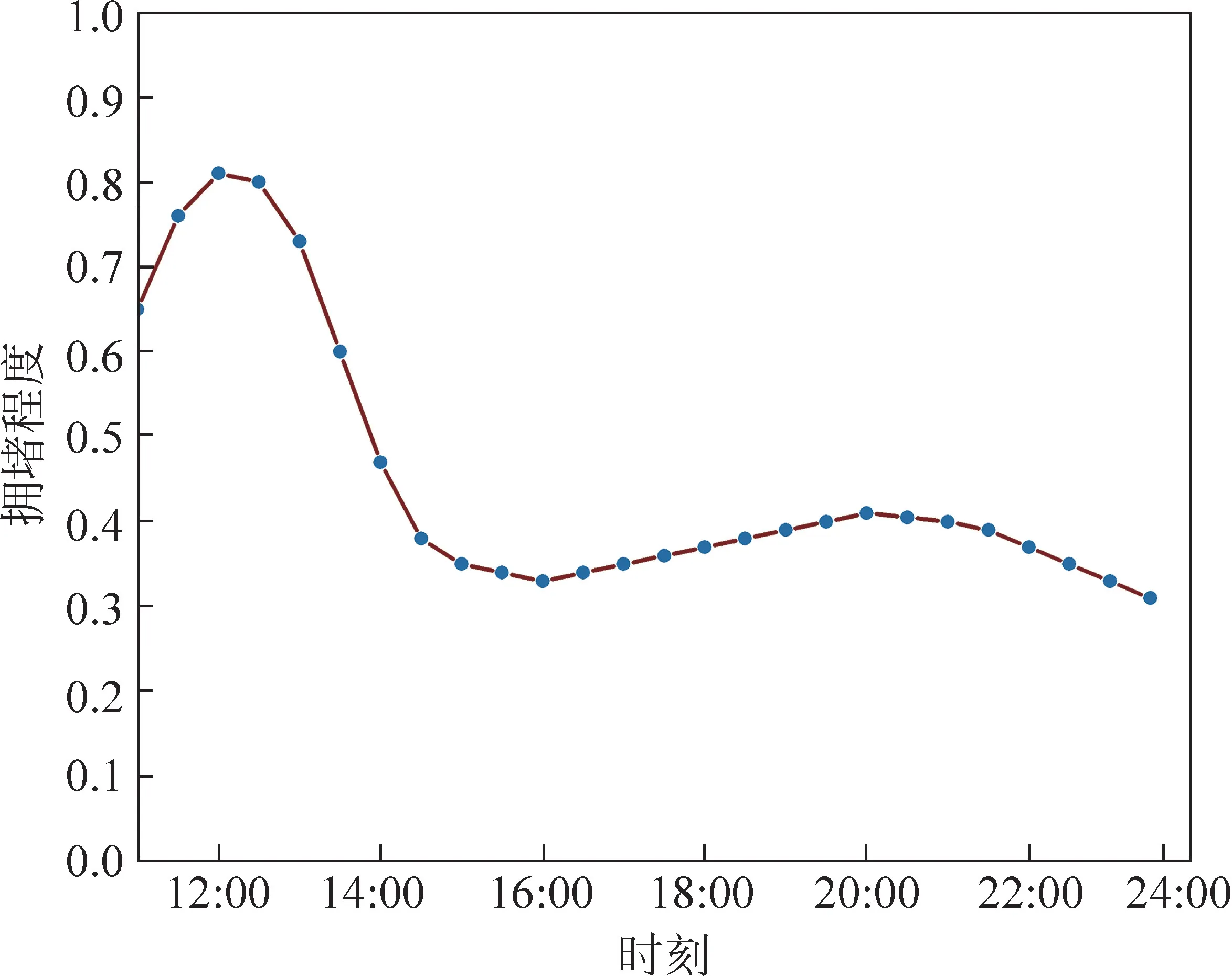
图4 交通网拥堵程度Fig.4 Congestion level of traffic network

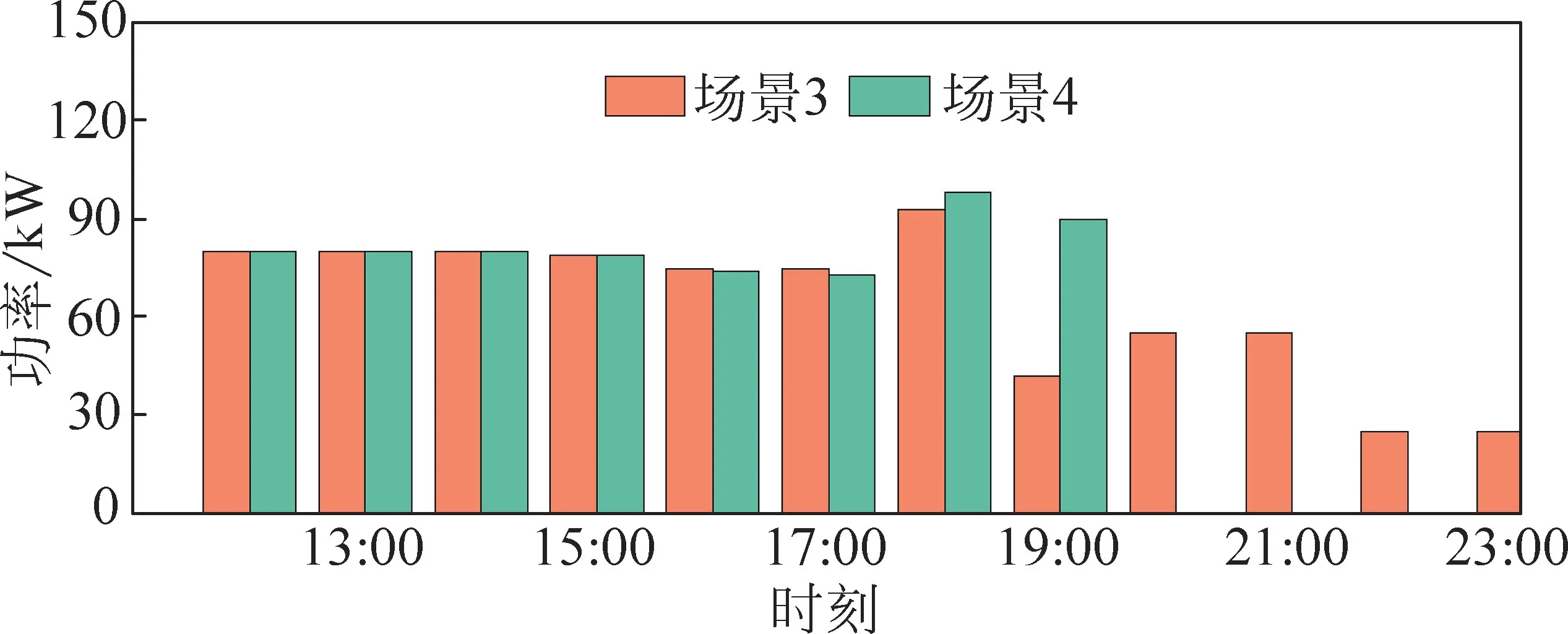
图5 场景3、4的弃负荷功率Fig.5 Abandoned load power for scenario 3 and 4

图6 DG有功出力Fig.6 Active outputs of DGs

由表3可知:在同样不考虑检修时间不确定性的场景2相比场景1而言,故障修复所需时间变长,但总成本减少了22.10%,弃负荷量减少了17.12%,二者均有明显的减少;而对于同样考虑检修路程不确定性的场景3、4,场景4故障修复时间多了2h,但是弃负荷量减少了465kW·h,场景3的总成本增加了15.24%。

考虑检修时间的不确定性和表3的各相弃负荷量,场景3、4的故障检修方案有明显区别。由图5可见:由于在前5个时段两者故障线路均没有被修复,故弃负荷量相同,在模拟的后4个时段场景4没有弃负荷量,在此之前第7个时段故障线路最后一段被修复并投入运行;而场景3在寻求最短时间的过程中未考虑检修线路对系统供电影响的重要程度,直到最后12时段,才修复完成最重要线路2-3段,因此模拟的任意时段都有弃负荷功率。由此可见,场景4可识别出对电力系统最重要的线路并优先修复,尽可能减小总的弃负荷量和总成本,对配电网弹性提升效果显著。

5 结论

针对极端天气下配电网系统的弹性恢复力提升问题,本文由DG和联络开关恢复短时供电,考虑极端天气对交通网的影响,由检修小组进行维修,提出一种故障发生后长短时间故障演变分析的两阶段RO模型。通过分析改进的IEEE 33节点配电网,该模型显著提升了配电网抵御极端天气的弹性能力。可得如下结论:

(1) 基于路径的最优化,本文建立的两阶段RO模型,综合考虑了长时间尺度故障修复和较短时间尺度,以减小弃负荷量;相较于不采用最优路径的恢复策略,利用C&CG算法求解的两阶段鲁棒模型能显著降低配电网的故障时间,尽可能快地完成了灾后恢复与重建,极大地提高了配电网在极端天气事件下的弹性恢复力。

(2) 灾后恢复阶段通过求解最优的检修路径,充分发挥了两阶段RO模型的优越性。通过考虑极端天气下检修路径的不确定性,做出了最优的故障修复决策,明显减小了负荷削减损失,提高了重要负荷的供电保障能力。