Improved Approaches Toward Analysis of Electromagnetic Processes in Electrodynamical Devices Based on the Theory of Electromagnetic Field

(Department of Automated Control Systems,Lviv Polytechnic National University,Lviv 79013,Ukraine)

Abstract: In the course of designing and developing different-purpose electrodynamical devices,electromagnetic processes in movable and immovable media need to be calculated simultaneously.The solution for such tasks based on the electromagnetic field theory is associated with the emergence of significant theoretical and practical difficulties.The problems that arise during the calculation of electromagnetic processes in movable and immovable media of electrodynamical devices using the electromagnetic field theory are examined in this study.Improved approaches toward the calculation of electromagnetic processes in electrodynamical devices using Maxwell’s equations are suggested.Notably,calculating electromagnetic processes in movable and immovable media using Maxwell’s equations necessitates consideration of the systems of coordinates where the electromagnetic phenomena are analyzed.Theoretically substantiated methods of calculating electromagnetic processes in movable and immovable media based on the principles of electromagnetic field theory are proposed.The methods consider the systems of coordinates where the analysis of electromagnetic phenomena is conducted.The effectiveness of the suggested methods for example in calculating electromagnetic processes in movable and immovable media of the turbogenerator is illustrated.

Keywords: Theory of electromagnetic field,movable and immovable media,systems of coordinates,mathematical modelling,electrodynamical

1 Introduction1

The analysis of electromagnetic phenomena in electrodynamic devices requires the simultaneous calculation of electromagnetic processes in various structures with distributed parameters: moving and stationary,linear and nonlinear,isotropic and anisotropic media.It is one of the most complicated problems of theoretical electrical engineering.To solve such a problem,it is necessary to simultaneously consider the following components of the electromagnetic field in the mathematical model: the effect of the given currents,the effect of the vortex field,and the effect of the mechanical motion of structural elements of the electrodynamical device.

The electromagnetic processes in electrodynamical devices can be calculated using (a) the theory of electromagnetic circuits,(b) a combination of the theory of electromagnetic circuits and theory of electromagnetic field,and (c) the theory of electromagnetic field.When there is no need for a detailed analysis of electromagnetic processes in all elements of the device structure or when the electrodynamical device is only considered a part of a more complicated system,to simplify the problem,developing mathematical models that operate on integral physical quantities (such as currents,voltages,and magnetic fluxes) is expedient[1-5].Notably,such models are unfit for full and comprehensive analysis of electromagnetic phenomena in electrodynamical devices,particularly in very bulky structural elements(in electrical pathways and magnetic cores).

In practice,for the analysis of electromagnetic phenomena in bulky electrical pathways and magnetic cores of electromagnetic devices using principles of the theory of electromagnetic circuits,spatial structures of devices are often replaced using chain equivalent circuits[6-10].The construction of chain equivalent circuits is based on the formation of conventional magnetic circuits with concentrated parameters (both for individual elements and the entire device).Such an approach is only considered suitable in rough approximation because it fails to guarantee the required adequacy and precision of space-time analysis of electromagnetic phenomena in movable and immovable media,as it allows for conventional division of real spatial structures of electrodynamical devices into conventional magnetic resistors connected in parallel and in series,creating conventional integral magnetic fluxes running through these connections.

Because the development of field mathematical models is theoretically and algorithmically complicated,the practical statement of the task can be simplified using a simultaneous application of the principles of both the theories of electromagnetic circuits and electromagnetic field in models for the calculation of electromagnetic processes in electrodynamical devices.This approach allows for a description of electromagnetic phenomena in bulky electrical pathways and in magnetic cores using the theory of electromagnetic field and in electric windings using the theory of electromagnetic circuits[11-15].

One of the most prospective trends of creating mathematical models is the sole use of the theory of electromagnetic field for the analysis of electromagnetic phenomena in movable and immovable media of electrodynamical devices[16-20].

Complexities in the development of field mathematical models of electrodynamical devices are caused by the following factors.

(1) The need to select suitable basic electromagnetic quantities on the basis of which the electromagnetic phenomena in movable and immovable media of devices are described in models (main vectorsH,E,B,Dor potentialsAandφof electromagnetic field).

(2) The need to consider the systems of coordinates,where the electromagnetic phenomena in movable and immovable media are mathematically described,in models.

(3) Complexity of the choice of such a system of coordinates where,within the investigation operating mode,analyzing electromagnetic processes in all the movable and immovable elements of structures of the electromagnetic device is least problematic.

(4) Possibility of practical determination of boundary conditions for equations of the electromagnetic field in movable and immovable,linear and nonlinear,as well as isotropic and anisotropic media considering actual physical peculiarities of electromagnetic phenomena in the device.

(5) Selection of effective ways to consider the nonlinear electric and magnetic characteristics of the materials of the device in mathematical models.

(6) Choice of values of discretizational grid steps that contribute to the formation of the minimal (as to the number of equations) system of calculation equations in mathematical models,leading to comprehensive consideration of the peculiarities of the structures of the device in the models.

(7) Making assumptions in the models that do not contradict the primary objective laws of electromagnetic processes in electrodynamical devices within the investigation operating mode and correspondently,do not lead to the distortion of actual electromagnetic phenomena.

(8) Other complexities.

All these factors not only cause the main complications in the development of field mathematical models of electrodynamical devices but also determine the adequacy and precision of the models developed.

In previous studies[21-24],a TGW-500 turbogenerator was selected for the approbation of different approaches toward mathematical modeling of electromagnetic processes in electrodynamical devices based on electromagnetic field theory methods.The aim of those studies was to investigate the influence of the substitution of equivalent continuous anisotropic media for the real teeth zones of the rotor (or stator or rotor and stator simultaneously) on peculiarities and on the character of transient and steady-state processes of the TGW-500 turbogenerator in no-load mode.

In this study,the problems that arise in the application of Maxwell’s equations for the calculation of electromagnetic processes in movable and immovable media of electrodynamical devices are considered.The reasons for obtaining equations[16-20]that fail to consider the coordinate systems of movable and immovable media are also considered.Such equations are often used in practice for mathematical descriptions of electromagnetic processes in movable media of electrodynamic devices.The possible cases of theoretically accurate application of Maxwell’s equations for calculation of electromagnetic processes in the movable media of electrodynamic devices have been analyzed.Therefore,improved approaches to mathematical description and calculation of electromagnetic processes in movable and immovable media of electrodynamic devices using Maxwell’s equations are suggested.In addition,we demonstrate the factors influencing the practical application of the obtained theoretical equations[16-20],which fail to consider the coordinate systems of movable and immovable media,for the calculation of electromagnetic processes in movable media of electrodynamic devices.To simplify the task-create model and to confirm the accuracy and effectiveness of the suggested methods,the development of a field mathematical model of a TGW-500 turbogenerator operating in idling (no-load) mode with equivalent teeth zones of the rotor and stator is considered.

2 Methods for mathematical modeling of electromagnetic processes in movable media based on the theory of electromagnetic field

Studies regarding the analysis of electromagnetic phenomena in electrodynamical devices based on the theory of the electromagnetic field[16-20]are of considerable theoretical and practical interest.Notably,the primary essential shortcoming of these studies is the fact that in the main calculation equations on the basis of which electromagnetical processes in movable and immovable media of electrodynamical devices are described in mathematical models,the systems of coordinates where vectors of the electromagnetic field are presented are not considered.

The most typical and general way of obtaining the calculation equations with the aim of mathematically describing electromagnetic processes in movable media,which is used in most studies devoted to the analysis of electromagnetic phenomena in electrodynamical devices (e.g.,Refs.[16-20]),fail to consider the systems of coordinates where the electromagnetic process is considered.Herein,we analyze the aforementioned approach in detail and ascertain theoretical preconditions of the emergence of such mistakes as well as possible ways of avoiding them.

We apply the first Maxwell equation[25]in the form

whereHis the vector of magnetic field strength;∇ is the Hamiltonian operator;andδis the vector of density of total current,as well as the known Lorentz-Poincare’s transformation[26]

whereE′ andEare the vectors of electric field strength in movable and immovable systems of coordinates,respectively;vis the vector of velocity of the medium movement (or movement of the system of coordinate);andBis the vector of magnetic induction.

If the fact that some vectors of the electromagnetic field are expressed in terms of coordinates of the movable system of coordinates (x′,y′,z′) and the other vectors are expressed in terms of coordinates of the immovable system of coordinates (x,y,z) is neglected,then Eq.(2) assumes the following form

We substitute the following equations[25]

whereAis the vector potential of the electromagnetic field;andφis the scalar potential,and the Lorentz-Poincare’s transformation in Eq.(3) into Eq.(1).Thus,the main equation used to mathematically describe electromagnetic processes in movable media in terms of vector and scalar potentials is obtained

whereνis inverse magnetic permeability;γis the electric conductivity of the medium,andεis the dielectric permittivity of the medium.

Eq.(5) can be rewritten as follows

Having accepted the assumption of quasi-stationarity of the electromagnetic field in electrodynamical devices,Eq.(6) is simplified as follows

In the case of the use of Wail’s gauging (φ=0),Eq.(5),primarily used to calculate electromagnetic processes in movable media of electrodynamical devices assumes the following form

Eqs.(5)-(8) and their different modifications are used in previous studies[16-20]for the analysis of electromagnetic phenomena in movable media of electrodynamical devices.In Eqs.(5)-(8),although there are no explicit relationships between the vectors of the electromagnetic field for movable or immovable systems of coordinates,two vector potentials of the electromagnetic field are simultaneously contained within a single equation,i.e.,A(x,y,z) andA(x′,y′,z′) denoted by the same letterA.Therefore,approaches toward the analysis of electromagnetic phenomena in movable media presented in Refs.[16-20] are difficult to justify from a theoretical point of view.

We follow the aforementioned sequence of derivations but consider theoretically accurate relationships between the vectors of the electromagnetic field and their corresponding(movable and immovable) systems of coordinates[21].

If electromagnetic processes in electrodynamical devices are calculated in the movable system of coordinates (x′,y′,z′),then the first Maxwell’s Eq.(1) for movable media assumes the following form

Considering the known Eq.(2) between vectors of electric field strength in movable and immovable media;Eq.(9) can be rewritten as follows

Considering Eq.(4),Eq.(10) can be rewritten[21]as follows

Assuming quasi-stationarity of electromagnetic processes in devices,Eq.(12) can be simplified as follows

Having set the gaugingφ=0 of the potentials of the electromagnetic field,Eq.(13) can be expressed as follows

Using the approaches presented in previous studies[16-20]to calculate the electromagnetic processes in movable media with the application of vector and scalar potentials,as well as appropriately considering the relationship between the vector fields in the equations and their corresponding systems of coordinates,we obtain Eqs.(11)-(14).These equations contain vector potentials of the electromagnetic field in movable and immovable systems of coordinates simultaneously (denoted byAandA',respectively),i.e.,within a single equation two unknown vectors are simultaneously present.As a result,using the system of equations obtained in the aforementioned way,calculating the electromagnetic processes in movable media is impossible.

Based on the above analysis of ways of obtaining Eqs.(5)-(8) and Eqs.(11)-(14) for the calculation of electromagnetic processes in movable media of electrodynamical devices,the following conclusions were drawn[21].

(1) In movable media,using Eqs.(5)-(8) or their various modifications,the accurate calculation of electromagnetic processes is impossible because these equations are not theoretically accurate.Therefore,for the mathematical description of electromagnetic phenomena at a chosen point of a movable or immovable medium of the electrodynamical device,whether we use Eqs.(5)-(8) or simultaneously use several individual differential or algebraic equations where the vector is related to a particular system of coordinates is not essential.

(2) The calculation of electromagnetic processes in movable media using Eqs.(11)-(14) or their various modifications obtained in a theoretically accurate and substantiated way is impossible because these equations,which are intended for mathematical description of electromagnetic process at a chosen point of a movable medium of the electrodynamical device,constitute two unknown variables (i.e.,within each individual equation): vector potentialA'of the electromagnetic field in the movable system of coordinates and vector potentialAof the electromagnetic field in the immovable system of coordinates.

(3) Independent of the choice of the set of electromagnetic vectors and a set of main variables for the calculational equations of field mathematical models of electrodynamical devices (the set of the main vectorsH,E,B,Dof electromagnetic field or potentialsAandφof electromagnetic field) to describe electromagnetic phenomena in movable media,direct substitution of the expression of the Lorentz-Poincare’s transformation in Eq.(2) into the main equations will lead to the emergence of electromagnetic vectors related to different systems of coordinates within a single equation.Using such a system of equations,calculating electromagnetic processes in movable media is impossible.Therefore,direct application of Lorentz-Poincare’s transformation in field mathematical models allows for the transfer of the known (obtained in any way) space-time distribution values of vectors of the electromagnetic field from a movable to an immovable system of coordinates or vice versa.However,this approach fails to facilitate determination of the necessary values of the field vectors both in the movable and immovable systems of coordinates.

Therefore,based on the aforementioned results,no theoretical possibility of applying a mathematical tool as optimal and comprehensive as Maxwell’s equations for the analysis of electromagnetic phenomena in movable media of electrodynamical devices exists.

The solution of the aforementioned problem is within its theoretical and mathematical foundations[21].

From a mathematical perspective,calculating the necessary values of vectors of electromagnetic field within a single movable or immovable medium,all the electromagnetic variables for this medium system of calculational equations need to be expressed in terms of a particular single movable or immovable system of coordinates.Correspondingly,the boundary conditions at all outer borders of the medium must be determined only in the chosen system of coordinates.Having solved the aforementioned system of equations,we obtain the unknown electromagnetic field vector values.When needed,the obtained results can be transferred using Lorentz-Poincare’s transformation into a movable or immovable system of coordinates.

Considering the aforementioned aspect,we formulate the following possible theoretically substantiated approaches toward the calculation of electromagnetic processes in all movable and immovable media of electrodynamical devices[21]: ①calculations can be performed in a single immovable system of coordinates;② calculations can be performed in a single movable system of coordinates;③calculations can be performed in any movable inertial system of coordinates that is not rigidly fixed to a medium of the device;④ in all zones of a device,calculations can be performed in systems of coordinates rigidly fixed to media,and the relative motion of movable and immovable media can consider a field mathematical model of electrodynamical devices in the determination of boundary conditions.

For the analysis of electromagnetic phenomena in such electrodynamical devices as a generator or an electric motor,the electromagnetic processes can be calculated as follows[21].

(1) In a single immovable system of coordinates rigidly fixed to the stator with Lorentz-Poincare’s transformation concerning space-time distributions of electromagnetic quantities in the zones of the rotor from the immovable system of coordinates into the movable system of coordinates rigidly fixed to the rotor.

(2) In a single movable system of coordinates rigidly fixed to the rotor with Lorentz-Poincare’s transformation concerning space-time distributions of electromagnetic quantities in the zones of the stator from the movable system of coordinates into the immovable system of coordinates rigidly fixed to the stator.

(3) In any other movable system of coordinates that is neither rigidly fixed to the rotor nor to the stator,with Lorentz-Poincare’s transformation concerning space-time distributions of electromagnetic quantities in the zones of the rotor from the movable system of coordinates into the system of coordinates rigidly fixed to the rotor,and in the zones of stator from the movable system of coordinates into the system of coordinates rigidly fixed to the stator.

(4) In the zones of the rotor in a system of coordinates rigidly fixed to the rotor,and in the zones of the stator in a system of coordinates rigidly fixed to the stator;the relative motion of movable and immovable media of rotor and stator can be considered in a field mathematical model in the determination of boundary conditions.

The variant of analysis of electromagnetic phenomena in a system of coordinates that is neither rigidly fixed to the rotor nor to the stator is the most complicated in the development of field mathematical models of such electrodynamical devices because it necessitates additional calculations associated with Lorentz-Poincare’s transformation of the results obtained from the chosen system of coordinates into systems of coordinates rigidly fixed to the rotor and stator.

The first two aforementioned approaches toward the calculation of electromagnetic processes in movable and immovable media of electrodynamical devices are the most effective because in the course of their application in field mathematical models,the relative mechanical motion of structural elements of the device is excluded.In addition,the need to use Lorentz-Poincare’s transformation from the chosen system of coordinates into a system of coordinates that is rigidly fixed to a certain body only emerges for the obtained vectors of the electromagnetic field in some zones.This considerably simplifies the process of analysis.

We consider practical application of the suggested methods of analysis of electromagnetic phenomena in electrodynamical devices based on the examples of calculation of electromagnetic processes in the cross-sectional zones of the TGW-500 turbogenerator in idling (no-load) mode.

3 Mathematical modeling and simulation of electromagnetic processes in a TGW-500 turbogenerator in idling mode in a single movable system of coordinates of the rotor

To confirm the applicability and accuracy of the suggested methods of calculating electromagnetic processes in movable media,we selected a TGW-500 turbogenerator and one of its simplest modes of operation,i.e.,idling (no-load) mode.The turbogenerator is a synchronous electrodynamical device where electromagnetic processes in idling mode are sufficiently studied and understandable from the point of view of their analysis both in a system of coordinates rigidly fixed to the rotor and one rigidly fixed to the stator.

The TGW-500 turbogenerator was designed and manufactured by the “Electrot’azhmazh” enterprise(Kharkiv city,Ukraine).

The main characteristics of the TGW-500 turbogenerator are presented in Tab.1.

Tab.1 Characteristics of the TGW-500 turbogenerator

To simplify the development of field mathematical models of the TGW-500 turbogenerator,the teeth zones of the rotor and stator,as well as the layered body of the stator,are replaced by equivalent continuous nonlinear anisotropic media.

In the course of developing the field mathematical models of the TGW-500 turbogenerator,the following assumptions are made: ①the displacement currents are not considered;② the electromagnetic field along the main axis of the turbogenerator is regarded as plane-parallel;③electromagnetic phenomena in butt-end zones of the device are not considered;④hysteresis phenomena in magnetic materials of the turbogenerator are not considered.

Fig.1 shows the arrangement of calculated zones of half a cross-section of a turbogenerator with equivalent tooth zones of rotor and stator.Considering the zone diagram given in Fig.1 with respect to the radii of elements of the structure of the device,R1is the radius relative to the rotor slot bottoms;R2is the external radius of the rotor;R3is the internal radius of the stator;R4is the radius relative to the stator slot bottoms;R5is the external radius of the stator;andR6is the radius of the air zone outside the turbogenerator.

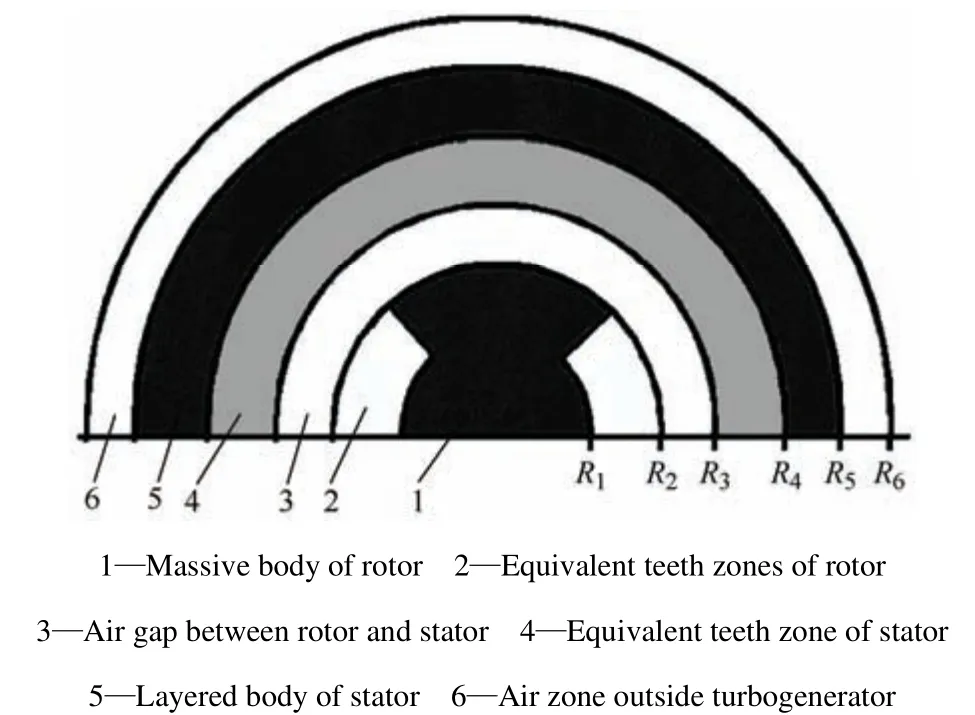
Fig.1 Primary calculations zones of the 1/2 cross-section of the turbogenerator

The main geometric dimensions of half the cross-sectional zone of the TGW-500 turbogenerator corresponding to Fig.1 are given in Fig.2.

Fig.2 Primary geometric dimensions of half the cross-sectional zone of the TGW-500 turbogenerator

In the course of developing a field mathematical model of the idling mode of a turbogenerator,choosing a system of coordinates that is rigidly fixed to the movable rotor as the main system is expedient because in this mode,the source of the electromagnetic field,and consequently,the driving force of all electromagnetic processes in the investigated device is the winding of the rotor.

The development of such a field mathematical model of the turbogenerator allows for the calculation of electromagnetic processes in the following zones:massive body of rotor,equivalent teeth zones of rotor,and in the air gap between the rotor and the stator in the system of coordinates rigidly fixed to the rotor.In the other cross-sectional zones of this device(equivalent teeth zone of the stator,equivalent zone of the layered body of stator,and air zone outside turbogenerator),we analyze electromagnetic phenomena in a system of coordinates chosen for the stator,this system of coordinates is rigidly fixed to the system of coordinates chosen for the rotor.

Considering the accepted assumption concerning the quasi-stationarity of electromagnetic processes in a turbogenerator,as well as considering the accepted gaugingφ=0 the electromagnetic field potentials,the equation for calculating electromagnetic phenomena in moving equivalent electrically conductive media of teeth zones of rotor is expressed as follows

For the calculation of electromagnetic processes in the massive electrically conductive medium of the rotor’s body,we use the simplified Eq.(15) expressed as follows

We mathematically describe the electromagnetic process in the zone of the air gap between the rotor and the stator using the following formula obtained using Eq.(16)

The electromagnetic process in the equivalent electrically conductive medium of the stator’s teeth zone is calculated as follows

whereA′ is the vector potential of the electromagnetic field chosen for the stator system of coordinates;this system is rigidly fixed to the rotor’s system of coordinates.

In the equivalent layered zone of the stator body,the electromagnetic process is mathematically expressed as follows

We calculate the values of functionin the air zone outside the turbogenerator in the chosen for the stator system of coordinates (this system is rigidly fixed to the rotor’s system of coordinates) based on the following equation

We recalculate electromagnetic characteristics of the equivalent media of teeth zones of the rotor and the stator as follows

wherevαandvrare the inverse magnetic permeabilities of the equivalent medium in tangential and radial directions,respectively;vfis the inverse magnetic permeability of the material of the teeth of rotor or stator;ν0is the inverse magnetic permeability of copper;γfis the electric conductivity of rotor or stator;γCuis the electric conductivity of copper;anddfandd0are the widths of the tooth and the slot of rotor,respectively;for the teeth zone of the stator,we also usedfandd0.

The magnetic characteristics of the equivalent zone of the layered body of stator is calculated as follows

whereνfandν0are the inverse magnetic permeabilities of the ferromagnetic sheet and the insulation of the layered body of the stator,respectively;anddfandd0are the widths of the sheet and the insulation,respectively.

The nonlinear electromagnetic characteristics of materials of the rotor and the stator are described using splines expressed as follows

According to technical data of the TGW-500 turbogenerator,its massive rotor is made of ST3-quality highly alloyed steel,and segments of its stator’s core of highly alloyed cold-rolled electrical steel of E330 quality.

Fig.3 depicts the curve of magnetizing the rotor material.

Having interpolated the electromagnetic characteristics given in Fig.3 and calculated the necessary values of coefficients concerning inverse magnetic permeability using Eq.(23),we obtain the following equations

The body and teeth of the stator are made of individual segments made of pressed sheets of ST3 electrical steel,whose magnetization curve is plotted in Fig.4.

Fig.4 Magnetization curve of material of the teeth and stator body made of highly alloyed ST3 steel

Because in equations of field mathematical models of turbogenerator,the inverse magnetic permeability of media is present,the interpolation of the electromagnetic characteristic of the ST3 material of the stator is made according to Eq.(23) as follows

Determining boundary conditions in field mathematical models of electrodynamical devices is significant.In the development of the field mathematical models of the TGW-500 turbogenerator in idling mode,to achieve fuller and more adequate mathematical description of physical laws of electromagnetic phenomena at outer boundaries along the radii of the pole pitch of the calculated zones of the turbogenerator’s cross-section,an improved approach toward determining boundary conditions is used.This approach allows for consideration of the fact that in the pole pitch of this device along the angular coordinate,both the vector potential and its first and second derivatives with respect to coordinateαare periodical[21].Considering the aforementioned factors,the boundary conditions at the outer boundaries of the zones along axisrare calculated as follows

whereHris the radial component of the vector of magnetic field strength.

We determine the values of functionz′Aat the outer conventional boundary of the air zone outside of the turbogenerator along axisαaccording to the following equation

whereiis the subscript corresponding to the node of the spatial grid in a cylindrical system of coordinates along the radius.

At all internal borders of the turbogenerator,the boundary conditions are determined using a classic approach toward describing the behavior of the vector of magnetic field strength at the interface of media with different electromagnetic characteristics

The voltage values on the phases of the stator’s winding of the turbogenerator are determined according to the following relationship

whereuiis the voltage of the phase of stator’s winding;wiis the number of turns of stator’s winding in each phase;lis the axial length of the windings;Az′siis the value of vector potential at the node of the grid of spatial discretization in the transformed system of coordinates of stator which belongs to the zone of the winding;andkiis the coefficient which considers the number of nodes belonging to the zone of the winding of the phase of stator.

The value of current in the rotor’s winding is determined according to the following equation[21]

whereif,uf,andrfare the current,voltage,and active resistance of the rotor’s winding,respectively;Lfis the scattered inductance of butt parts of the rotor’s winding;wfandlrare the number of turns and axial length,respectively,of the rotor’s winding;AzRiis the value of vector potential in the rotor’s system of coordinates at the node of the grid that belongs to the zone of rotor’s winding;andkfis the coefficient that considers the number of nodes that belong to the zone of rotor’s winding.

If necessary,considering Eq.(2) and having accepted the assumption of the plane-parallel electromagnetic process in the turbogenerator in its operation in idling mode,we can convert the obtained space-time distributions of values of axial componentzA′ of vector potential of electromagnetic field in the equivalent teeth zone of stator,in the equivalent zone of the layered body of the stator,as well as in the air space zone outside the turbogenerator from the system of coordinates rigidly fixed to the rotor into the system of coordinates rigidly fixed to immovable stator according to the following equation[21]

whereAzstis the axial component of the vector potential of the electromagnetic field in the immovable stator’s own system of coordinates andωis the angular speed of the rotor’s rotation.

Upon integrating the left and right sides of Eq.(30),we obtained the following equation

whereAz st(t) is the vector potential of the electromagnetic field in the system of coordinates of the immovable stator;(t) is the vector potential of the electromagnetic field in the media of the stator in the system of coordinates rigidly fixed to the movable rotor;(t) is the increment of the vector potential of the electromagnetic field in the media of the stator in the system of coordinates rigidly fixed to the movable rotor;this increment is along the angular coordinate relative to a certain fixed point of the stator.

In electrodynamics,the application of the Eq.(31)to convert the values of the vector potential of the electromagnetic field from one system of coordinates to another is reduced to a shift of the obtained spatial distribution of functionalong angular coordinate on the value corresponding to actual mutual position of movable and immovable media in the given fixed instant of time.

During these investigations,practical use of existing(developed for the calculations of electromagnetic processes in electrotechnical devices) commercial software packages was impossible.However,even if such a possibility existed,the state-of the art software packages,hinder the calculation of electromagnetic processes in a TGW-500 turbogenerator on the basis of the proposed field mathematical models.This is because in the existing commercial software packages,the electrodynamics of motion of media of electrodynamical devices is mathematically described based on the methods of electromagnetic circuit theory but not the electromagnetic field theory.For the calculation of electromagnetic processes in the TGW-500 turbogenerator on the basis of the suggested field mathematical models,it is necessary to implement in algorithms and in computer programs the relative motion of media of the rotor and stator with simultaneous calculation values of vectors of electromagnetic field in the media based on the basis of Maxwell’s equations.Unfortunately,performing such algorithms using currently existing commercial software packages (even using such a widely used commercial software package as “Ansys”) is rather difficult.For the aforementioned reasons,there was no other way of developing novel (created in the author’s own way) algorithms and computer programs for calculating electromagnetic processes in all zones of the TGW-500 turbogenerator (operating in idling mode) based on mathematical models proposed herein.The computer programs were developed using the“Fortran 90” programming language.

By developing a system of coordinates of the movable rotor,the field mathematical model of the turbogenerator as well as the real parameters of the TGW-500 turbogenerator,a computer simulation of transient electromagnetic processes in the cross-sectional zones of this device in idling mode was performed.In the model,the rotor winding of turbogenerator is connected to the voltage ofuf=141 V.

The electromagnetic processes in the cross-sectional zones of the turbogenerator were calculated using the following algorithm.

Step 1: Having the values of the spatial distributions of the function of the vector potential of electromagnetic fieldsAandA′ in the cross-section zones of the turbogenerator in the corresponding coordinate systems at the timet(in the case oft=0,we use the initial values of the spatial distributions of the function of the vector potential of electromagnetic fieldAandA′ in the cross-section zones of the turbogenerator in the corresponding coordinate systems) using Eqs.(24)-(26),we determine the boundary conditions for functionsA,A′ on all internal and external boundaries of the calculation zones of the device in the corresponding coordinate systems.

Step 2: Using Eqs.(21)-(23),we identify the values of the inverse magnetic permeability and electrical conductivity of the media for all cross-sectional zones of the turbogenerator.

Step 3: Based on Eqs.(15)-(20),we identified new values of the spatial distributions of the function of the vector potential of electromagnetic fieldsAandA′ in the cross-sectional zones of the turbogenerator in the corresponding coordinate systems for timet=t+Δt.

Step 4: Using Eqs.(27)-(29),we determine the value of the voltage of the phases of the stator windings and the current in the rotor winding at timet=t+Δt.

Step 5: We increase the current time by the value Δt(t=t+Δt),if the current timetis less than the specified calculation timeT,we apply step 1,ift≥T,the calculation is completed.

As this mathematical model involves calculation in one rotor coordinate system,the movement of the rotor media relative to the stator media is disregarded when implementing the algorithm.

In Figs.5-8,some of the obtained space-time distributions of values of electromagnetic quantities in a pole pitch of cross-section zones of TGW-500 turbogenerator in idling mode are shown.The aforementioned distributions of values of electromagnetic quantities over time and over space were plotted using the “Surfer” software package.

In the presented spatial distributions,the values of electromagnetic quantities at nodes of the coordinate grid along the radii correspond (as to the node’s ordinal number) to the following zones of the turbogenerator’s cross-section: 0 … 54 is the zone of massive ferromagnetic body of rotor;54 … 75 are equivalent teeth zones of the rotor;75 … 87 is the zone of air gap between the rotor and stator;87 …117 is the equivalent teeth zone of the stator;117 …174 is the zone of the body of the stator;174 … 186 is the air zone outside the turbogenerator.The number of nodes of the grid of spatial discretization along the angular coordinate in the pole pitch of the calculated turbogenerator’s cross-section zones is 192.

4 Mathematical modeling and simulation of electromagnetic processes in the TGW-500 turbogenerator in idling mode in rotor and stator coordinate systems simultaneously

We consider the development of a 2-D field mathematical model of the turbogenerator with equivalent rotor’s and stator’s teeth zones in idling mode in the rotor’s and stator’s systems of coordinates simultaneously.The distinction of this model from the one proposed in the previous chapter is the fact that the electromagnetic processes in the rotor’s zones are mathematically described in terms of coordinates of a system that is rigidly fixed to the rotor,and the stator’s zone electromagnetic processes are mathematically described in terms of coordinates of a system that is rigidly fixed to the immovable stator.In addition,such an approach toward the calculation of electromagnetic processes in movable and immovable media of electrodynamical devices allows for the inclusion of the mechanical movement of the rotor’s media (along the angular coordinate) in the model relative to the stator’s media.

We calculated the electromagnetic field in the equivalent teeth zones and in the massive body of the rotor according to Eqs.(15) and (16),respectively.In these equations,componentAzof the vector potential of the electromagnetic field is expressed in terms of the coordinates of a system of coordinates that is rigidly fixed to the movable rotor.In the other cross-section zones of the turbogenerator,the obtained values of functionAzare expressed in terms of coordinates from a system that is rigidly fixed to the immovable stator.

In the idling mode of the turbogenerator,the electromagnetic processes in equivalent media– in the teeth zone and body of the stator– are expressed using the following equation[21]

whereAzis the axial component of the vector potential of the electromagnetic field in the immovable stator system of coordinates.

The electromagnetic processes in the air gap zone between the rotor and stator,as well as in the air zone outside the turbogenerator is calculated using the following equation

whereAzis the axial component of the vector potential of the electromagnetic field in the immovable stator system of coordinates.

The boundary conditions outside the borders of the zones along axisrcalculated using Eq.(24).

In the air zone outside the turbogenerator,the boundary condition for componentAzof the vector potential of the electromagnetic field is calculated as follows

At all inner borders of the cross-section zones of the device,the boundary conditions are calculated using Eq.(26).

The electromagnetic characteristics of equivalent continuous anisotropic media of the rotor’s and stator’s teeth zones,as well as those of the stator’s layered body,are determined using Eqs.(21)-(22).

In the field mathematical model of the turbogenerator,the consideration of nonlinear properties of the rotor’s and stator’s magnetic materials is implemented using splines based on Eq.(23).

The values of current in the rotor’s winding were calculated using Eqs.(28) and (29).

The voltage values of on the phases of the stator’s winding were calculated according to the following equation

whereAzsiis the axial component of the vector potential of the electromagnetic field in the stator’s system of coordinates.

The field mathematical model of the turbogenerator in idling mode developed in the rotor’s and stator’s systems of coordinates simultaneously allows for algorithmic implementation of mechanical motion of the media of rotor relative to the media of stator through displacement of nodes of the spatial discretizational grid of rotor relative to nodes of spatial discretizational grid of stator considering the following condition

whereαΔ represents the discretizational grids of rotor and stator along the angular coordinate;andtΔ represents the step of numerical integration of the system of differential equations with respect to time.

Notably,to observe condition Eq.(36) and simplify the development of the field mathematical model of the turbogenerator in movable and immovable media’s own systems of coordinates simultaneously,the values of stepsαΔ of discretizational grids of the rotor and stator are equalized.

Generally,in the simultaneous development of field mathematical models of electrodynamical devices in the rotor’s and stator’s systems of coordinates,when the need to choose grids of spatial discretization with different steps for the media of the rotor and the stator arises,or in when the angular speed of rotor’s rotation relative to stator is not constant,interpolation of the vector potential of the electromagnetic field in both sides of the boundary between movable and immovable media is necessary.

Interpolation of the values of functionAzat a boundary between the movable and immovable zones allows for the development of more universal field mathematical models in movable and immovable media systems of coordinates when there are structural elements in electrodynamical devices that can move at different speeds or change to the opposite direction of motion during operation.

Using the mathematical model developed in the rotor’s and stator’s systems of coordinates simultaneously,the computer simulation of electromagnetic processes in the media of the cross-section of the TGW-500 turbogenerator operating in idling mode under the given voltage ofuf=141 V on the rotor’s winding is performed.

The electromagnetic processes in the cross-sectional zones of the turbogenerator are calculated using the following algorithm.

Step 1: Having the values of the spatial distributions of the function of the vector potential of electromagnetic fieldAin all cross-sectional zones of the turbogenerator in the physical coordinate systems of the rotor and stator at timet(in the case oft=0,we use the initial values of the spatial distributions of the function of the vector potential of electromagnetic fieldAin all cross-sectional zones of the turbogenerator in the physical coordinate systems of the rotor and stator) using Eqs.(24),(26),(34) we find the boundary conditions for functionsAon all internal and external boundaries of the calculation zones of the device in the physical coordinate systems of the movable rotor and stationary stator.

Step 2: Using Eqs.(21)-(23),the value of the inverse magnetic permeability and the value of the electrical conductivity of the media for all cross-sectional zones of the turbogenerator.

Step 3: Based on Eqs.(15),(16),(32),(33),we obtain new values of the spatial distributions of the function of the vector potential of the electromagnetic fieldAin the cross-sectional zones of the turbogenerator in the physical coordinate systems of the rotor and stator for the moment of timet=t+Δt.

Step 4: Using Eqs.(28),(29),and (35),we obtain the value of the current in the rotor winding and the voltage value of the phases of the stator windings at the timet=t+Δt.

Step 5: We increase the current time by the value Δt(t=t+Δt),if the current timetis less than the specified calculated timeT,we go to step 1 (at the same time,we algorithmically shift the rotor media relative to the stator media on the angular value Δαin the direction of rotor movement),ift≥T,the calculation is completed.

In Figs.9-10,some of the obtained space-time distributions of values of electromagnetic quantities in the pole pitch of the cross-sectional zones of the TGW-500 turbogenerator in the idling mode are presented.

During computer simulation,the value of voltage on the rotor’s winding,geometric sizes of calculational zones,electromagnetic characteristics of the media,and spatial steps of grids of discretization of the rotor and stator were set to be the same as in the case of calculation of the turbogenerator’s idling mode with the application of the field mathematical model developed in Section 3.The description of the correspondence of numeration of nodes along coordinatesrandαin the distributions of values of electromagnetic quantities in the media of a turbogenerator’s cross-section to nodes of the grid of spatial discretization of zones of structure of the TGW-500 device is discussed in Section 3.

5 Analysis of results of calculations

The results obtained using a single system of coordinates of the rotor mathematical model of the turbogenerator allow for the analysis of the transient and steady-state electromagnetic processes in all zones of the device operating in idling mode;the analysis is from the perspective of observation from the rotor’s system of coordinates.

In the idling mode of the turbogenerator,there is no conduction current in the windings of the stator,i.e.,there is no electromagnetic reaction of the stator’s windings to the mechanical motion of the rotor and to the electromagnetic processes in the rotor.Therefore,in the analysis of the electromagnetic phenomena in the device,it principally does not matter whether the rotor is rotating or resting in a fixed position relative to the stator.Therefore,from the perspective of observation from the rotor’s system of coordinates,the qualitative and quantitative character of the transient and steady-state electromagnetic processes in all zones of the turbogenerator will be the same for the movable and immovable rotor.Therefore,for the analysis of transient and steady-state processes in the turbogenerator in idling mode,the development of field mathematical models of the device in the system of coordinates rigidly fixed to the movable rotor is the most expedient and effective.This has been confirmed in practice by the results obtained on the basis of mathematical model of the turbogenerator in idling mode in the rotor’s system of coordinates.Using this model,the long-lasting transient electromagnetic processes (up to their steady state) in all zones of the turbogenerator operating in idling mode were calculated.In Figs.5-8,the steady-state space-time distributions of values of electromagnetic vectors in the cross-sectional zones of the TGW-500 turbogenerator in idling mode are presented.

Developing such a model is considerably easier than developing a field mathematical model of a turbogenerator in the rotor’s and stator’s systems of coordinates simultaneously,because the calculation of electromagnetic phenomena in zones of a device in a single movable or immovable system of coordinates does not allow for algorithmic implementation of mechanical motion of nonlinear anisotropic media of rotor relative to nonlinear anisotropic media of stator.Herein,as considered in Section 3,conversion of values of the axial component of vector potential of the electromagnetic field in equivalent zones– teeth zone and body of stator– from the transformed one into the stator’s own system of coordinates is made by shifting of the obtained spatial distributions of values of the functionzA′ alongα-axis by the necessary angular incrementαΔ of the coordinate.Theoretically,in a field mathematical model of a turbogenerator that is developed in a rotor’s system of coordinates (according to the actual electromagnetic process),the corresponding actual mutual situation of the media of the rotor and stator at fixed timetis reproduced.

When comparing the character and values of the spatial distribution of magnitude of vector of magnetic induction in cross-sectional zones of the turbogenerator shown in Fig.5,namely,in the equivalent teeth zone and in the body of the stator,with corresponding distributions that are depicted in Figs.9-10,the spatial distributions of values of |B| in these media in Figs.9-10 are evidently shifted relative to the spatial distribution of values of magnitude of vector of magnetic induction shown in Fig.5 along the angular coordinate by the value that corresponds to actual mutual situation of the rotor and stator at fixed timet.

Fig.5 Spatial distribution of values of magnitude of magnetic induction vector in pole pitch of the turbogenerator’s cross-section zones in rotor’s system of coordinates at time t=700.00 s in the transient process of the idling mode

Fig.6 Spatial distribution of values of radial component of magnetic induction vector in pole pitch the turbogenerator’s cross-section zones in the rotor’s system of coordinates at time t=700.00 s in the transient process of the idling mode

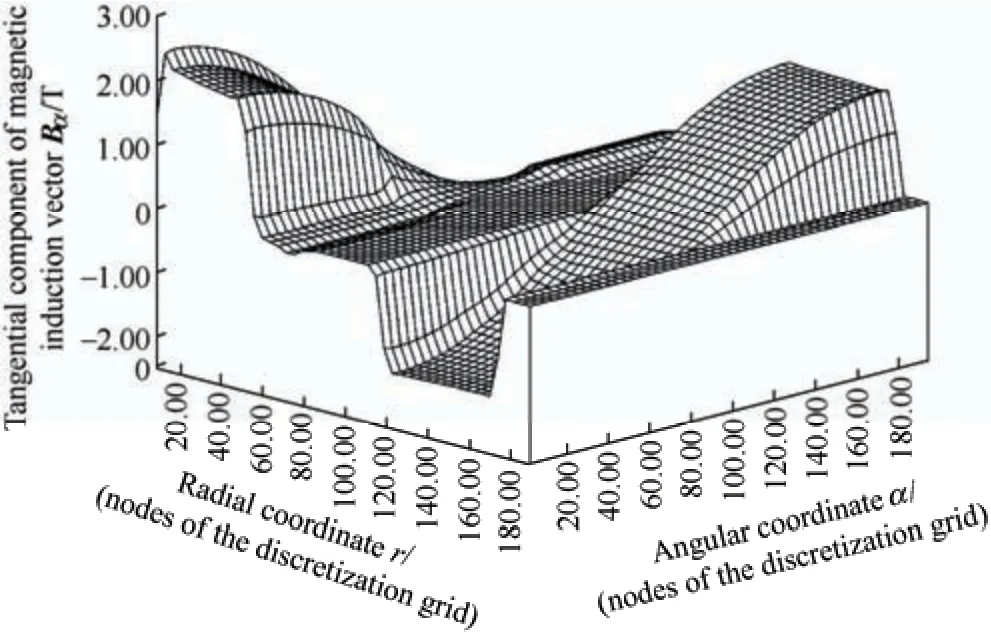
Fig.7 Spatial distribution of values of tangential component of magnetic induction vector in pole pitch of the turbogenerator’s cross-section zones in the rotor’s system of coordinates at time t=700.00 s in the transient process of the idling mode

Fig.8 Spatial distribution of values of axial component of vector potential of electromagnetic field in pole pitch of the turbogenerator’s cross-section zones in the rotor’s system of coordinates at time t=700.00 s in the transient process of the idling mode

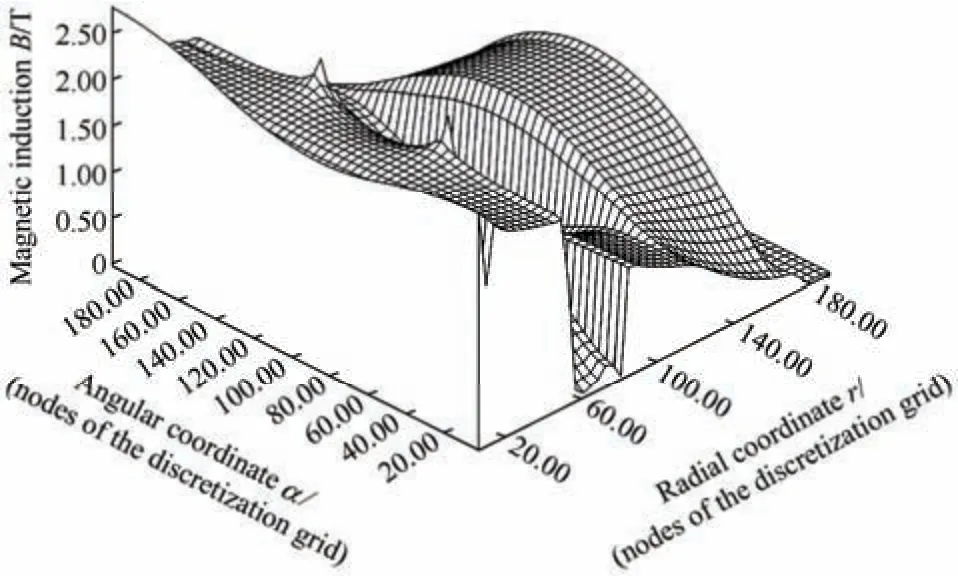
Fig.9 Spatial distribution of values of magnitude of vector of magnetic induction in the pole pitch of the cross-sectional zones of the turbogenerator in the rotor’s and stator’s systems of coordinates at time t=700.015 43 s of the transient process of the idling mode

Fig.10 Spatial distribution of values of magnitude of vector of magnetic induction in the pole pitch of cross-sectional zones of the turbogenerator in the rotor’s and stator’s systems of coordinates at time t=700.017 66 s of the transient process of the idling mode

Fig.11 Spatial distribution of values of magnitude of magnetic induction vector in pole pitch of zones of the turbogenerator’s cross-section in the rotor’s system of coordinates at time instant of t=700.024 5 s in transient process of idling mode

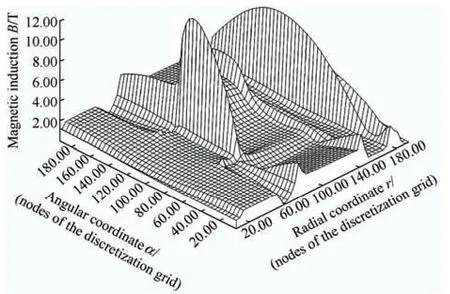
Fig.12 Spatial distribution of values of magnitude of magnetic induction vector in pole pitch of zones of turbogenerator’s cross-section in rotor’s system of coordinates at time instant of t=700.087 s in transient process of idling mode

Therefore,the spatial distributions of the magnitude of the vector of magnetic induction in the cross-sectional zones of the turbogenerator depicted in Fig.5 and Figs.9-10,that are obtained using field mathematical models developed in the rotor’s system of coordinates and in the rotor’s and stator’s own systems of coordinates simultaneously,are in full compliance with the logic and results of theoretical investigations discussed in Sections 2,3,and 4.

As indicated by the results of the computer simulation of the idling mode of the turbogenerator using field mathematical models developed both in a single system of coordinates of rotor and in a rotor’s and stator’s own systems of coordinates simultaneously,the relative error of the difference between the calculations using these two models values of the components of vectors of electromagnetic field in the cross-sectional zones of the pole pitch of the device at discrete times during a full revolution of media of rotor relative to the media of stator and in any of their mutual collocation is less than 1%.This fact once more confirms that for the analysis of the idling mode of this class of electrodynamical devices,developing their field mathematical models in a single system of coordinates rigidly fixed to a movable or immovable medium is expedient.

Particular attention should be paid to the spatial distributions of values of magnitude of vector of magnetic induction in the pole pitch of the cross-sectional zones of the turbogenerator depicted in Figs.11-12.These distributions are obtained using the field mathematical model of the turbogenerator in idling mode with equivalent teeth zones of the rotor and stator,a model developed in the rotor’s system of coordinates.In the model for the calculation of electromagnetic processes in electrically conductive equivalent teeth zone of stator (e.g.,Refs.[16-20]) we used Eq.(8).In this equation,the vector potential of the electromagnetic field is neither related to the rotor’s nor to the stator’s system of coordinates.

Figs.11-12 show a considerable magnetic skin-effect in the electrically conductive surface of the rotor’s massive body and in those of the equivalent teeth zones of the rotor,as well as essential increase in the values of magnitude of vector of magnetic induction in the equivalent electrically conductive teeth zone of the stator,which are not characteristic of the idling mode of the device.This visually confirms that from the theoretical and from practical points of view,the application of Eq.(8) for mathematical description and the calculation of electromagnetic processes in movable media of electrodynamical devices is not accurate.

Notably,the steady-state spatial distributions of values of electromagnetic field vectors in the cross-section of the turbogenerator,and corresponding values of voltages on the winding phases of the stator in the idling mode of the device obtained using the models in Sections 3-4 differ from the corresponding spatial distributions of values of field vectors and corresponding values of the voltages on the windings phases of the stator of the real TGW-500 turbogenerator using the value of the relative error of approximately 23%.As indicated by study results,the cause of this is a replacement of the real structures of teeth zones of the rotor and the stator with the equivalent nonlinear anisotropic media in the course of the development of the field mathematical models of the turbogenerator in idling mode.This problem warrants further research and is beyond the scope of the present study.

As shown by additional calculations,in the case of a fixed rotor (results obtained using a mathematical model of the device developed in the rotor coordinate system),at the corresponding fixed times,the electromagnetic process in all cross-sectional zones of the turbogenerator in the rotor coordinate system is the same as that when the rotor rotates (results obtained using a mathematical model of the device developed in the physical coordinates of the rotor and stator simultaneously).From a theoretical point of view,this is justified,because in the idle mode of the turbogenerator,there is no electromagnetic reaction of the rotor windings to the mechanical movement of the stator.Therefore,the spatial distributions of the electromagnetic field in all zones of the device in the rotor coordinate system are the same whether the rotor is rotating or stationary.

6 Conclusions

The results of mathematical modelling and simulation of electromagnetic processes in cross-sectional zones of the turbogenerator have indicated that in the course of developing mathematical models of electrodynamical devices using the methods of electromagnetic field theory,disregarding the distinction of the systems of coordinates of movable and immovable media,where the calculation of electromagnetic phenomena are conducted,is unacceptable.Disregarding this important theoretical,physical,and mathematical entity of electromagnetic processes in the application of the principles of electromagnetic field theory for the formation of a system of equations leads to distortion by models of actual electromagnetic phenomena in movable and immovable structural elements of electrodynamical devices in the investigated modes of their operation.

The analysis of the results of computer simulation of electromagnetic processes in the cross-sectional zones of the turbogenerator obtained using field mathematical models of the device with equivalent teeth zones of rotor and stator (these models have been developed in the system of coordinates of the movable rotor and in the systems of coordinates of the rotor and stator simultaneously) indicated that in the course of the development of field mathematical models of electrodynamical devices in idling mode,where we deal with spatial symmetry or periodicity of structures of movable and immovable parts,the calculation of electromagnetic phenomena in a single movable or single fixed system of coordinates is the most optimal.

To simplify the analysis of electromagnetic processes in movable and immovable zones of electrodynamical devices in a single movable or fixed system of coordinates,choosing as the basic system,a system of coordinates where forcing sources of the electromagnetic field are immovable is expedient.