On the Nature of Long Period Radio Pulsar GPM J1839-10: Death Line and Pulse Width
H.Tong
School of Physics and Materials Science, Guangzhou University, Guangzhou 510006, China; tonghao@gzhu.edu.cn
Received 2023 July 27; revised 2023 October 2; accepted 2023 October 11; published 2023 November 15
Abstract Recently another long period radio pulsar GPM J1839−10 has been reported, similar to GLEAM-X J162759.5−523504.3.Previously,the energy budget and rotational evolution of long period radio pulsars had been considered.This time,the death line and pulse width for neutron star and white dwarf pulsars are investigated.The pulse width is included as the second criterion for neutron star and white dwarf pulsars.It is found that:(1)PSR J0250+5854 and PSR J0901−4046 etc.should be normal radio pulsars.They have narrow pulse width and they lie near the radio emission death line.(2)The two long period radio pulsars GLEAM-X J162759.5−523504.3 and GPM J1839−10 are unlikely to be normal radio pulsars.Their possible pulse width is relatively large.They lie far below the fiducial death line on the P P˙- diagram.(3)GLEAM-X J162759.5−523504.3 and GPM J1839−10 may be magnetars or white dwarf radio pulsars.At present, there are many parameters and uncertainties in both of these possibilities.
Key words: stars: magnetars – (stars:) pulsars: general – (stars:) pulsars: individual (GPM J1839−10)
1.Introduction
Pulsars are rotating magnetized neutron stars(Lyne&Graham-Smith 2012).Their rotation period can range from milliseconds to several seconds(Young et al.1999).The period of magnetars can be as large as 12 s (Olausen & Kaspi 2014).Recently, there are new discoveries toward the long period end of pulsars.PSR J0250+5854 is the slowest radio pulsar at that time,with a period of 23.5 s(Tan et al.2018).Later more radio pulsars with periods larger than 10 s are discovered (Han et al.2021).The rotational evolution of these long period radio pulsars may evolve physics in the magnetosphere or magnetic field decay(Kou et al.2019).The central compact object inside supernova remnant RCW 103 showed magnetar activities and was confirmed to be a magnetar with a period of about 6.6 hr(D’Ai et al.2016;Rea et al.2016).Its rotational evolution may require a magnetar spin-down by a fallback disk (Tong et al.2016).However, the magnetar inside RCW 103 is radio-quiet.It is not sure why it is radio-quiet, e.g.,beaming or no radio emission at all.
The long period radio pulsar (dubbed as LPRP) is pushed forward by the discovery of GLEAM-X J162759.5−523504.3(GLEAM-X J1627 for short, Hurley-Walker et al.2022).GLEAM-X J1627 has a period of 1091 s (about 18 minutes)and it is a transient in radio.The existence of LPRPs is further strengthened by PSR J0901−4046 with a period of 76 s(Caleb et al.2022).However,it is not certain whether these LPRPs are neutron stars or white dwarfs.For such slow rotators,it is more natural that they are white dwarfs (Katz 2022; Loeb &Maoz 2022).At the same time,similar to the case of RCW 103 magnetar, these LPRPs may also be magnetar+fallback disk systems (Ronchi et al.2022; Tong 2023).At present, their nature remains unclear (Rea et al.2022).
A source similar to GLEAM-X J1627 has been recently reported, GPM J1839−10 (Hurley-Walker et al.2023).GPM J1839−10 has a pulsation period of 1318 s(about 21 minutes).Compared with GLEAM-X J1627, GPM J1839−10 has (1) a more stringent period derivative upper limitP˙ <3.6×10-13s s-1(Hurley-Walker et al.2023),which can place more constraint on the pulsar death line.(2) Its radio emission has lasted for more than 30 yr.This can enable later more monitoring.
For the energy budge and rotational evolution of GPM J1839−10, similar calculations can be applied to it as that for GLEAM-X J1627 (Katz 2022; Loeb & Maoz 2022; Ronchi et al.2022; Tong 2023).Since their periods are similar(21 minutes verse 18 minutes), the same conclusion may also be applied to GPM J1839−10,i.e.,magnetar+fallback disks or white dwarf pulsars.We will not repeat the calculations here.This time, we focus on (1) the death line for neutron star and white dwarf pulsars,(2)pulse width of LPRPs.From these two aspects, we want to discuss the nature of GPM J1839−10,which is the most recent example of LPRPs.
2.Model Calculations
2.1.Death Line for Neutron Star and White Dwarf Pulsars
The death line for radio emission of normal pulsars and magnetars has been discussed in Section 2.5 in Tong (2023).The potential drop at a specific angle across the polar cap is simply a classical electrodynamics exercise.For normal radio pulsars with a dipole magnetic field,the maximum acceleration potential across the polar cap is(Ruderman&Sutherland 1975;Zhou et al.2017):
where Bpis the surface magnetic field at the pole region(which is two times the equatorial value,Lyne&Graham-Smith 2012),R is the stellar radius,Ω is the star’s angular velocity.When the maximum acceleration potential equals 1012V, it is defined as the radio emission death line.Below the death line, the star is not expected to have radio emissions.The value of 1012V is only a fiducial value.A rough estimation of the physics evolved is that (Ruderman & Sutherland 1975): an electron accelerated in such a potential attains a Lorentz factor about γ ∼106.This electron may emit curvature photons of energy
These curvature photons may be converted to electron-position pairs in strong magnetic fields.If the electron Lorentz factor (i.e.,acceleration potential)is lower,the curvature photons may have energy less than 1 MeV.The subsequent pair production process cannot continue.This may result in a cease of the radio emission (i.e., radio emission death line).
For a magnetar+fallback disk system, the magnetosphere may be modified by (1) the fallback disk if the disk is still active, (2) the magnetar’s twisted magnetic fields.If the death line is modified by the fallback disk, the corotation radius will replace the light cylinder radius as the maximum radial extent of the field lines.The corresponding maximum acceleration potential and death line are presented in Equation(10)in Tong(2023):
where Rlc=Pc/(2π) is the neutron star’s light cylinder radius,is the corotation radius.If the death line is modified by the twist of the field lines, a twisted field line will result in a larger polar cap and a larger potential drop.The maximum acceleration potential and death line for a twisted magnetic field are presented in Equation (12) in Tong(2023):
where n is a parameter characterizing the twist of field lines.n=1 corresponds to the dipole case (for n=1, the equation returns to the dipole case Equation (1)).0 For white dwarf pulsars, it is possible that they have similar magnetospheric precess to that of neutron star pulsars(Zhang & Gil 2005; Katz 2022).However, there are several changes in the definition of death line (Equation (1)) for white dwarf pulsars. 1.For a typical neutron star, the radius is usually set to be 10 km.For a typical white dwarf (Figure 5.17 in Camenzind 2007), it has a radius of one percent the solar radius 0.01 R⊙(the corresponding white dwarf mass is about 0.8 M⊙). 2.The torque of a rotating magnetized object can be approximated as magnetic dipole braking (Xu &Qiao 2001).The star’s magnetic field can be obtained from the period and period-derivative measurement,which is a crude estimate of the star’s true magnetic field.Assuming a perpendicular rotator, the magnetic field is where B is the equatorial magnetic field at the surface(it is two times smaller than the polar magnetic field), I is the star’s moment of inertia.For typical neutron stars, with I ≈1045g cm2, R ≈106cm, it is the commonly cited formula for radio pulsars: For white dwarfs, assuming a typical mass of 0.8 M⊙and radius of 0.01 R⊙, the white dwarf’s moment of inertia is about 3×1050g cm2.Therefore, the characteristic magnetic field for a white dwarf pulsar is: This formula will be employed when drawing the death line on thediagram. 3.From Equation (2), a minimum Lorentz factor (i.e.,acceleration potential) is required to generate curvature photons with energy higher than 1 MeV.In the case of white dwarfs, the stellar radius is larger.The curvature radius of the magnetic field line is also larger,which is the order of(r is the emission height,Xu&Qiao 2001).Therefore,a higher acceleration potential may be required,e.g., as high as 1013V in Equation (1).The exact value depends on the detailed modeling of the white dwarf’s magnetosphere (as in the case of neutron star pulsars). The death line for normal radio pulsars, magnetars and magnetar+fallback disk systems is shown in Figure 1,along with GPM J1839−10 and other LPRPs.Figure 1 is updated from Figure 2 in Tong(2023).The death line for white dwarf pulsars is so different from that of the neutron star case that it is shown separately in Figure 2.φmax= 1012V and φmax= 1013Vare shown respectively.The characteristic magnetic field for white dwarf pulsars is also shown,for B=108G and B=109G.Most of the presently observed pulsating white dwarfs have magnetic fields smaller than 109G(Zhang&Gil 2005;Marsh et al.2016;Katz 2022; Pelisoli et al.2023). Figure 1.Definition of death line and distribution of long period radio pulsars(red circles)on the P–P˙diagram.The fiducial pulsar death line, the death line for a twisted magnetic field (n=0.8), and the death line modified by the fallback disk are also shown.Updated from Figure 2 in Tong (2023). GPM J1839−10 has a period of 1318 s.The single pulse varies in a pulse window 400 s (Hurley-Walker et al.2023).Similar things also happen in normal radio pulsars and radio emitting magnetars (Levin et al.2012; Yan et al.2015; Huang et al.2021).At present, the integrated pulse profile of GMP J1839−10 is not available.From previous experiences in pulsars and magnetars,the pulse window may be an estimate of the integrated pulse width.Then the pulse width of GPM J1839−10 is PW ≈400/1318=30%of the pulse phase(in this case,the pulse width may also be called the duty cycle, Tan et al.2018).If this is the pulse width of GPM J1839−10,it can also constrain the nature of the source. For normal radio pulsars,the colatitude of the last open field line at emission height r is: The emission beam radius is 3/2 times the angle θopen(Equation (17.9) in Lyne & Graham-Smith 2012): Figure 2.Definition of death line and contour of constant magnetic field for white dwarf pulsars.Two death lines are shown, with φm ax = 1013V (upper one) and φm ax = 1012V (lower one) respectively.Two contours of constant magnetic field are shown, with B=109 G and B=108 G respectively.The limiting Keplerian period for a typical white dwarf pulsar is also shown. The emission height of normal radio pulsars is always less than 100 times the neutron star radius (Johnston et al.2023).Therefore, the emission height in Equation (9) can be set as 100R, where R is the stellar radius.The observed pulse width depends also on the inclination angle α(angle between rotation axis and line of sight), and impact angle β (closest approach between the magnetic axis and the line of sight).The impact angle may always be a small quantity,in this case,the observed pulse width is related to the emission beam radius as(Equation(15.2) in Lyne & Graham-Smith 2012): In terms of pulse phase, the observed pulse width is: A small inclination angle α can result in a large pulse width. For a magnetar+fallback disk system, the calculation is similar to the calculations for death line.If the magnetosphere is regulated by the fallback disk, the corotation radius replaces the role of light cylinder radius in Equation(11).For a twisted magnetic field, the colatitude of the last open field line will be larger (Equation (11) in Tong 2023).The pulse width in units of pulse phase is: Figure 3.Theoretical pulse width as a function of period.The pulse width is in units of pulse phase.From bottom to top are: normal radio pulsars (black),magnetars with twisted magnetic field (dashed blue, for n=0.5), magnetar+fallback disk systems(solid blue),and white dwarf pulsars(green).Since the inclination angle is unknown, the plotted pulse width is actually PW ×sin α.For a small α, the actual pulse width can be larger. For n=1, the above equation returns to the dipole case(Equation (11)).For a white dwarf pulsar, the expression for the pulse width is the same as Equation (11), except that the stellar radius should be the white dwarf radius. The theoretical pulse width for normal pulsars, magnetar+fallback disk systems, and white dwarf pulsars is shown in Figure 3.Magnetars and white dwarf pulsars have wider pulse width compared with that of normal radio pulsars.This is especially true for LPRPs. From the death line on theP P˙- diagram, the LPRP GPM J1839−10 cannot be normal radio pulsars.A twisted magnetic field or the presence of a fallback disk can help to lower the position of the death line on theP P˙- diagram.The quantitative result depends on the parameters involved, e.g.,the twist parameter n.Figure 1 shows the death line for a twisted magnetic field with n=0.8.For a more twisted magnetic field (i.e., n=0.5), the position of the death line is lower on theP P˙- diagram.However, the typical untwisting timescale may be smaller, which may have difficulties in explaining why GPM J1839−10 can have radio emissions lasting more than 30 yr.A magnetar+fallback disk system may be consistent with the position of GPM J1839−10 on thediagram.However, the generation of radio emission in the presence of an active fallback disk is uncertain, although there are such possibilities (see Section 2.5 in Tong 2023 for discussions). The death line for white dwarf pulsars is also consistent with the position of GPM J1839−10 on theP P˙- diagram.However, there may be three constraints for white dwarf pulsars: (1) The maximum acceleration potential for white dwarf pulsars may be higher,e.g.,as high as 1013V.(2)White dwarf pulsars generally have magnetic field lower than 109G(Zhang&Gil 2005;Marsh et al.2016;Katz 2022;Pelisoli et al.2023).(3) For a white dwarf with mass 0.8M⊙and radius 0.01R⊙, the limiting Keplerian period is: These three constraints will limit the existence of white dwarf pulsars to a small triangle on thediagram, see Figure 2.Such a triangle of parameter space may explain why there are so few white dwarf radio pulsars (LPRPs are the only candidates). The pulse with of GPM J1839−10 is unknown at present.If its pulse window represents its pulse width, then it will have a pulse width of 30%.From the theoretical pulse width, normal radio pulsars may have difficulties in explaining the pulse width of GPM J1839−10.The solution in the normal radio pulsar case is that they should have an extremely large emission height.For a twisted magnetic field or magnetar+fallback disk system, the pulse width is larger, typically several percent.A small inclination angle or a slightly higher emission height may explain the possible observed pulse width of GPM J1839−10.White dwarf pulsars can naturally have larger pulse width. By combining the death line and pulse width requirement,it is unlikely that GPM J1839−10 is a normal radio pulsar.It is possible that GPM J1839−10 is a magnetar (including a magnetar+fallback disk system) or a white dwarf pulsar.For these two possibilities, there are many parameters at present.This conclusion is consistent with previous calculations for GLEAM-X J1627, based on energy budget and rotational evolution(Katz 2022;Loeb&Maoz 2022;Ronchi et al.2022;Tong 2023).Population synthesis of neutron star and white dwarf pulsars also get similar conclusions (Rea et al.2023). Comparison with other LPRPs.All three LPRPs PSR J2144-3933(Young et al.1999),PSR J0250+5854(Tan et al.2018),and PSR J0901−4046 (Caleb et al.2022) have a very narrow pulse width, typically less than 1%.Assuming a maximum emission height of 100R (Johnston et al.2023), the theoretical upper limit on pulse width is (Equation (11)): Therefore,PSR J0250+5854(with a period of 23.5 s)and PSR J0901−4046 (with a period of 76 s) etc.are consistent with a normal radio pulsar origin,from the pulse width point of view.However, both of GLEAM-X J1627 and GPM J1839−10(Hurley-Walker et al.2022, 2023) showed possible signatures of a large pulse width.Therefore, we propose that the pulse width of LPRPs may be taken as the second criterion in identifying their nature, in addition to their relative position to the death line on theP P˙- diagram.If a future LPRP has a narrow pulse width consistent with that of normal radio pulsars,it may be viewed as an extreme radio pulsar.All we have to do is to consider the corresponding magnetospheric physics involved, e.g., the definition of the death line, etc.If an LPRP has a large pulse width, then we must consider the possibility of magnetars or white dwarf pulsars. Comparison with other radio emitting magnetars.Radio emitting magnetars generally have a large pulse width compared with normal radio pulsars (Levin et al.2012; Yan et al.2015; Huang et al.2021).Especially, the single pulse width of magnetars are generally very narrow.They may vary randomly in the pulse window, therefore resulting in a wide integrated pulse width(Levin et al.2012;Yan et al.2015).We think this may also be the case of GPM J1839−10: narrow single pulse and a wide pulse window.From the pulse width point of view, the two LPRPs GLEAM-X J1627 and GPM J1839−10 are similar to radio-emitting magnetars. Maximum period of LPRPs.From Figures 1 and 2(or Figure 1 in Rea et al.2022),the existence of maximum magnetic field in combination with the death line implies there is a maximum period for radio-emitting neutron stars and white dwarfs.For neutron stars, the maximum magnetic field may be about 1016G.The definition of death line is rather uncertain (which will result in a death valley).However, the possible maximum period for radio emission may be around 104s or so.In this respect,the magnetar inside RCW 103(with a period of 6.6 hr)is not expected to have radio emissions.For white dwarfs,assuming of a maximum magnetic field of 109G,the expected maximum period may be about several thousand seconds.Future LPRPs with longer periods may help to unveil their nature, i.e., neutron stars or white dwarfs. Comparison with previous works.Observationally, GPM J1839−10 is similar to that of GLEAM-X J1627 (Hurley-Walker et al.2023).It confirms the existence of LPRPs as subpopulation of radio pulsars, which may deserve more future searches.Theoretically,the modeling for GPM J1839−10 may seem similar to that of GLEAM-X J1627.Compared with previous theoretical works (Ronchi et al.2022; especially Tong 2023), the present work has two outstanding: (1) The death line is extended to the case of magnetar’s twisted magnetic field and magnetar+fallback disk system in previous works.Here, the pulsar death line is extended to the white dwarf pulsar case, considering possible physics involved during the definition of the death line.(2) The pulse width is newly included in this work.We propose that it may be taken as the second criterion concerning the nature of LPRPs, in addition to that of timing parameters (e.g., period, periodderivative, death line, etc).By combining the rotational evolution, energy budget, death line, and pulse width, something is already clear for LPRPs: (1) For PSR J0901−4046(Caleb et al.2022),etc.with a period less than 76 s,they can be understood in the normal radio pulsar domain.(2) For the two LPRPs GLEAM-X J1627 and GPM J1839−10(Hurley-Walker et al.2022,2023),they are unlikely to be normal radio pulsars.Whether they are magnetars or white dwarf pulsars,they remain inconclusive at present. By considering the four aspects together (rotational evolution and energy budget in previous works, death line and pulse width in this work),it is found that:(1)PSR J0250+5854(Tan et al.2018) and PSR J0901−4046 (Caleb et al.2022)should be normal radio pulsars.They have narrow pulse width and they lie near the radio emission death line.Further investigations of their magnetospheric physics are required.(2)The two LPRPs GLEAM-X J1627 and GPM J1839−10(Hurley-Walker et al.2022, 2023) are unlikely to be normal radio pulsars.Their possible pulse width is relatively large.They lie far below the fiducial death line on thediagram.(3)GLEAM-X J1627 and GPM J1839−10 may be(a)magnetars with twisted magnetic field or magnetar+fallack disk systems,or(b)white dwarf radio pulsars.At present,there are many uncertainties in both of these possibilities.More multiwave observations are required in order to tell whether they are magnetars or white dwarfs. Acknowledgments H.Tong would like to thank Dr.Huang Zhi-Peng and Yan Zhen for discussions on pulse width and emission height.This work is supported by National SKA Program of China (No.2020SKA0120300) and the National Natural Science Foundation of China (NSFC, 12133004). ORCID iDs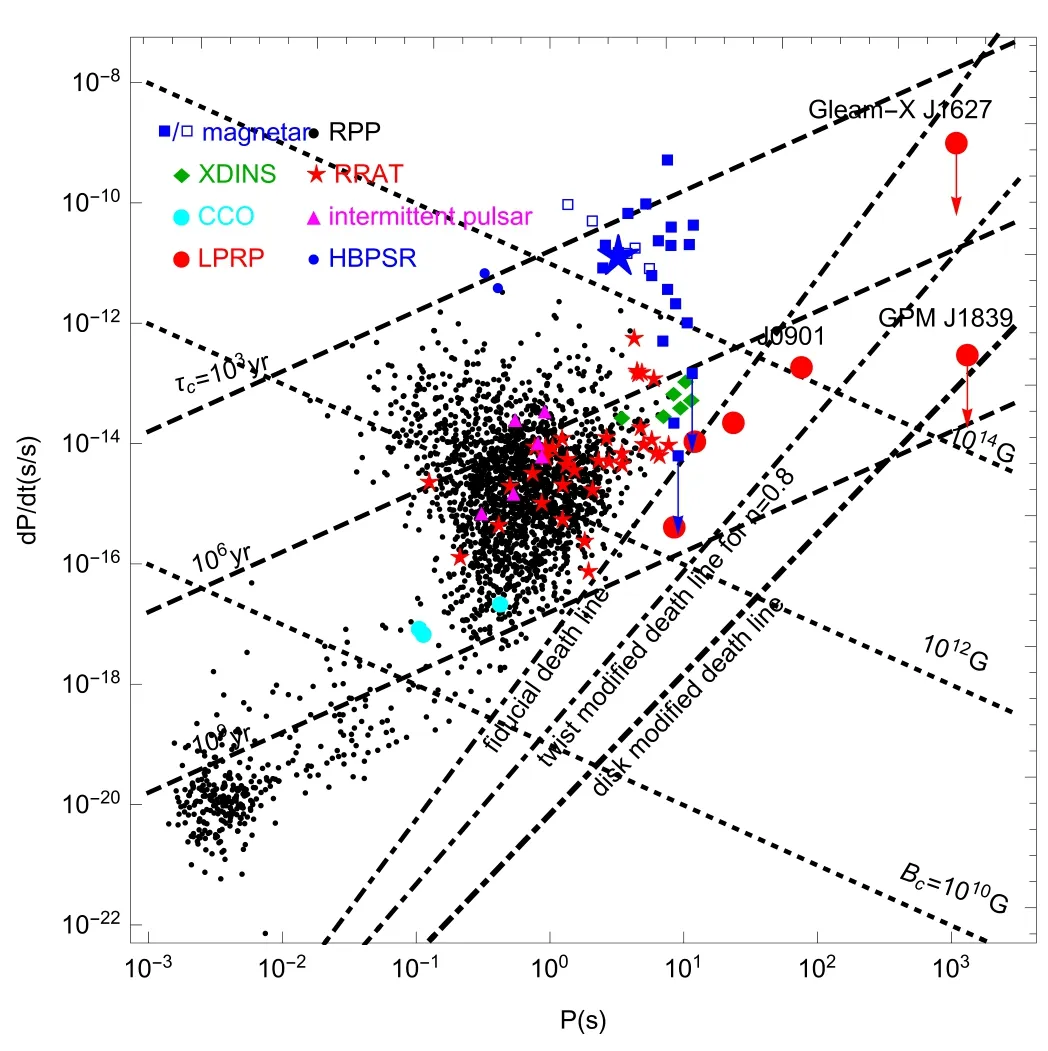
2.2.Pulse Width


2.3.On the Nature of GPM J1839-10
3.Discussion
4.Conclusion
 Research in Astronomy and Astrophysics2023年12期
Research in Astronomy and Astrophysics2023年12期
- Research in Astronomy and Astrophysics的其它文章
- Effect of Matching Algorithm and Profile Shape on Pulsar Pulse Time of Arrival Uncertainties
- A Revised Graduated Cylindrical Shell Model and its Application to a Prominence Eruption
- Predicting Gravitational Waves from Jittering-jets-driven Core Collapse Supernovae
- Redshift Dependence of the Low-energy Spectral Index of Gamma-Ray Bursts Revisited
- A Novel Imaging Method Based on Reweighted Total Variation for an Interferometer Array on Lunar Orbit
- PyMsOfa: A Python Package for the Standards of Fundamental Astronomy(SOFA) Service
