改进的蜉蝣优化算法的经济负荷分配

李国成,黄春兴,甘德俊,倪百秀

(皖西学院 金融与数学学院,安徽 六安 237012)

经济负荷分配(Economic Load Dispatch,ELD)问题是电力系统中一个重要优化问题[1]。它在过去的几十年里引起了许多研究人员的关注,当前仍然是电力系统领域的研究热点。该问题旨在确定发电机组的负荷分配方案,以最小化电力系统的总成本或满足负荷需求的同时最大化经济效益。在考虑了阀点效应、发电机运行约束和禁止运行区域等各种约束后,这种经济调度问题呈现出多约束、非凸、非线性和非光滑等特征[1,2]。

为了解决ELD问题,学术界提出了多种优化方法和算法。传统的方法包括基于数学规划的方法,如线性规划[3]、非线性规划[4]、混合整数规划[5]、动态规划[6]和分位数回归法[7]等,可以准确地建立ELD问题的数学模型,采用相应的算法进行求解,但在处理大规模系统时存在计算复杂度高的问题。近年来,随着人工智能技术的快速发展,智能算法在ELD问题中得到了广泛应用,如遗传算法[8]、粒子群优化算法[9,10]、蚁群算法[11]、微分进化算法[12]、闭环文化粒子群算法[13]、混沌优化算法[14]、生物地理学算法[15]、鲸鱼优化算法[16]、哈里斯鹰优化算法[2]、黏菌算法[17]、人工电场算法[18]、白鲸优化算法等[19],它们通过模仿自然界的进化和群体行为来搜索全局最优解。这些算法通过自适应搜索策略和多样化的搜索操作,在ELD问题求解中展现了较好的优化性能,并取得很好的实际应用效果。

随着数学规划方法和智能优化算法的不断发展,研究人员不断探寻用更加高效、更为精确和更低廉成本的方法来求解经济负荷分配问题,以提高电力系统的经济性、可靠性和环境友好性。本文基于精英策略构建一种改进的蜉蝣优化算法,该算法在寻优阶段具有很好的全局勘探能力和局部开发能力,收敛速度更快,可以更好地解决电力系统经济负荷分配问题。

一、问题描述与数学模型

(一)问题描述

经济负荷分配问题是在满足用户用电需求、保证电力系统正常运行的条件下,对各个发电机的功率进行最优配置,从而使整个系统的发电成本达到最低。从数学角度来看,该问题是一类具有多约束、单目标的非线性优化问题[8]。

(二)数学模型

如果系统总发电费用记为TC,系统内发电机总数为N,第i台发电机的有功功率为Pi,第i台发电机费用特性函数为Fi(Pi),则经济负荷分配问题的目标函数可表述为:

(1)

其中,当考虑阀点效应的费用时,第i台发电机费用特性函数Fi(Pi)为:

(2)

式(2)中ai,bi,ci,ei,fi分别为机组发电机中第i台的费用参数。本文考虑电网传输损耗与和供需平衡约束和考虑电网传输损耗和阀点效应作为能耗函数计算总成本两种情形。发电机组的运行功率限值约束条件为:

(3)

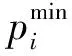
(4)

式(4)中,PD为系统内的总负荷。

二、改进的蜉蝣优化算法

(一)蜉蝣优化算法

蜉蝣优化算法(mayfly optimization algorithm,MA)是Konstantinos Zervoudakis于2021根据蜉蝣的飞行和繁衍行为规律提出的一种算法[20]。蜉蝣优化算法中的种群分为雄性和雌性,其中雄性的行为与粒子群相似,通过全局最优和自身历史最优进行移动,雌性则向优于自身的配偶进行移动,若其配偶弱于自己则自行局部搜索,然后这对雌性个体和雄性个体结合产生两个后代,并将较优个体保留在群体中。部分文献的研究结果表明[21,22],蜉蝣优化算法存在收敛速度较慢和易陷入局部最优解的不足。为此,本文基于精英策略对蜉蝣优化算法进行改进以提高其优化性能和收敛速度。蜉蝣优化算法步骤归纳如下[20]:

步骤1:设置种群规模,确定搜索空间,随机生成雄性蜉蝣的初始种群x0和速度vx0,雌性蜉蝣的初始种群y0和速度vy0,并设置终止条件。

步骤2:评估种群,计算各蜉蝣的适应度函数值,寻找群体最优Pbest和全局最优gbest。

步骤3:迭代前期(T<0.5×Tmax),雄性种群的速度更新公式为:

(5)

式(5)表示雄性蜉蝣被雌性蜉蝣吸引和没有被雌性所吸引两种情形下的速度更新,雄性蜉蝣位置更新公式为:

(6)

雌性蜉蝣速度更新公式为:

(7)

式(7)表示雌性蜉蝣被雄性蜉蝣吸引和未被雄性蜉蝣吸引两种情形下的速度更新,雌性蜉蝣位置更新公式为:

(8)

(9)

此处的吸引力是由适应度函数值来决定的,f(yij)>f(xij)表示雌性蜉蝣被雄性蜉蝣个体吸引,反之,则没有被吸引;假定最优的雌性蜉蝣个体被最优的雄性蜉蝣个体吸引,第二优雌性蜉蝣个体被第二优雄性蜉蝣个体吸引,以此类推。

步骤4:迭代后期:(T>0.5×Tmax),定义概率

(10)

其中,fnew为当前退火阶段的种群个体适应度;以概率p对速度进行调整;T为退火温度,这里设置为100,如果f(yi)>f(xi),以式(2)和式(4)进行速度更新;如果f(yi)≤f(xi),以概率p>rand(0,1)接受个体间吸引更新速度方式,否则,更新进度:

(11)

采用模拟退火机制,不仅保持了算法的高效更新模式,而且加快了算法的寻优速度,同时也增加了群体的多样性。

步骤5:个体排序后进行交叉和变异产生子代:

其中L为一特定区间生成的随机数,用以调节父代和母代的遗传系数。

步骤6:分离雄性和雌性蜉蝣,更新种群最优和全局最优,否则返回步骤 2,直至符合结束条件为止。

(二)基于精英策略改进的蜉蝣优化算法

蜉蝣优化算法收敛速度和搜索精度并不理想[21],在最优解的搜索过程中也容易产生滞后现象[22],受海洋捕食者算法[25]中精英策略的启发,本文构建改进的蜉蝣优化算法(improved mayfly optimization algorithm,IMA),其中精英策略被引入MA以提高其收敛速度。精英蜉蝣在IMA在不同的步骤更新策略中采用了不同的步骤更新策略搜索异性蜉蝣。类似于海洋捕食者算法,IMA的精英政策规则应用为:

(1)当T≤0.5×Tmax时

其中ei代表精英i蜉蝣位置,si是步长和RB是一个随机向量,每个向量分量由布朗运动获得的定义运算符 “⊗” 与上述相同。R表示向量在[0,1]中生成的统一随机数。

(2)当T>0.5Tmax时

其中RL是一个随机向量,每个分量都是通过分配获得。自适应参数CF,用于控制精英s的步长,可描述为:

(20)

(三)测试实验与结果分析

为了验证所构造的改进的IMA算法的优化性能,本文选取6个经典的标准测试函数进行测试实验,并与MA算法进行对比。6个标准测试函数的名称、数学表达式、定义域和最优值如表1所示,搜索空间的维数设置为:d=30.

表1 六个标准测试函数的定义

两种算法的参数设置参考ZERVOUDAKIS K的研究成果[20],雄性蜉蝣、雌性蜉蝣和子代蜉蝣的种群规模均为40,最大迭代次数为1000,实验独立运行30次,统计实验所得最优值的均值和标准差如表2所示,两种算法求解结果对比胜出者以粗体标识。

表2 六个标准测试函数的求解结果与对比

从表2可以看出,基于精英策略改进的蜉蝣优化算法(IMA)的优化性能有所改善,寻优的精度的以提高。与MA相比,改进后的IMA在对六个基本测试函数的30次独立运行测试实验结果表明其均值和标准差两个指标都胜出,表明改进后的算法求解精度更高,稳定性也更好,而且除了函数F2外,其他5个函数的测试结果都显示这种改进的效果是非常明显。这一点也可以从图1所描绘的两种算法求解六个函数的搜索迭代过程的收敛特征曲线对比观察到,同时我们也可以从图1看出改进后的IMA算法收敛速度更快。

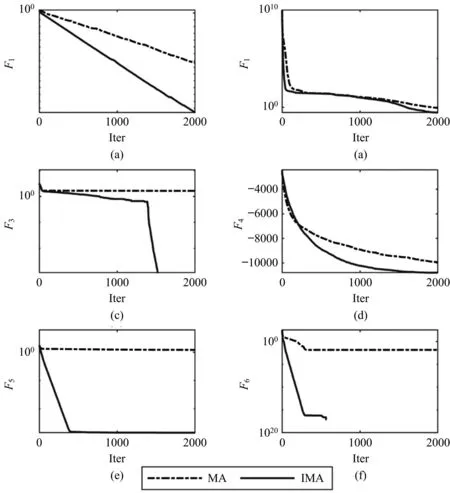
图1 MA和IMA收敛特征曲线对比

三、改进的蜉蝣优化算法求解经济负荷分配问题

(一)适应度函数的表示

利用蜉蝣优化算法来求解电力系统负荷分配,其种群个体即为待优化的发电机组的输出功率向量pop=(p1,p2,…,pM),i=1,2,…,n,目标是最小化发电机组能量消耗之和,因此由式(1)可以定义第i个蜉蝣个体的适应度函数如下:

(21)

若考虑阀点加载效应,则相应地式(21)可改写为:

(22)

(二)约束处理

电力负荷分配问题的典型约束条件通常包括容量约束和电力供需平衡约束。本文只考虑这两种约束的处理,其中容量约束,可通过设置个体位置变量来加以实现,即设置其上下界为:

(23)

电力供需平衡约束通过引入拉格朗日乘子λ,在目标函数里增加惩罚项,加以处理。因此,相应地式(21)和(22)可以改写为:

其中惩罚系数λ本文设置为106。

四、实证研究

为了验证蜉蝣优化算法求解经济负荷分配问题的可行性与有效性,本文选取了三个经典测试案例(http://www.al-roomi.org)来进行研究,分别是3、6、15个发电机组的电力系统经济负荷分配问题。

(一)三个机组的电力负荷分配问题求解

三个机组的电力负荷分配问题的总负荷为PD=850 MW,各发电机的参数见表3所示。

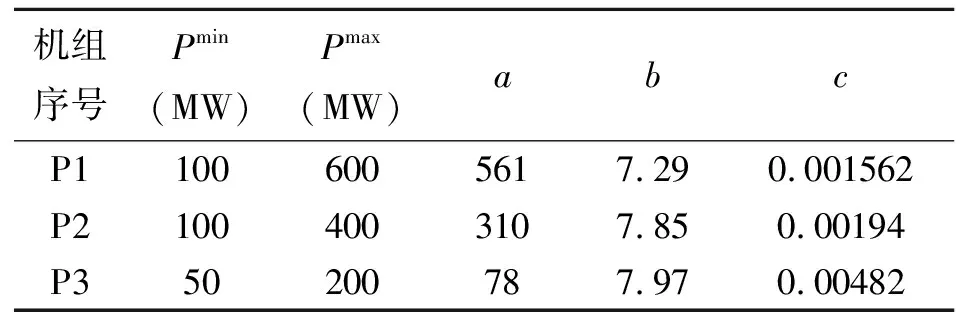
表3 三个发电机机组的参数

三个发电机机组的传输损耗系数矩阵为:

B0i=[0.01890 -0.00342 -0.007660],

B00=0.40357.

在案例一中,本文分为只考虑电网传输损耗与和供需平衡约束和考虑电网传输损耗和阀点效应作为能耗函数计算总成本两种情形作为能耗函数计算总成本,借助IMA 算法求解该案例,并与遗传算法(GA)[8]、两种改进的粒子群优化算法(CPSO、CLPSO)[13]以及混沌优化算法(COA)[14]等算法进行对比,种群规模为40,最大迭代次数为2000,三种算法在求解案例时独立运行30次,比较最差、平均和最好目标函数值,结果如表4所示。

表4 三个机组电力系统的最差、最好目标函数值

表5给出遗传算法(GA)、两种改进的粒子群优化算法(CPSO、CLPSO)、混沌优化算法(COA)以及改进蜉蝣优化算法(IMA)五种算法求解3个机组的电力负荷分配问题的结果。对比结果可以发现本文所采用的IMA 求解所得的最优机组负荷分配的总能耗成本是最少的。因而IMA 求解结果最优,其次是改进的粒子群优化算法CPSO、CLPSO,求解结果最差的是GA,其损耗明显高于其他算法的总成本。结果表明了蝗虫优化算法求解电力负荷分配问题是可行的,而且取得了不错的效果,总成本更低。

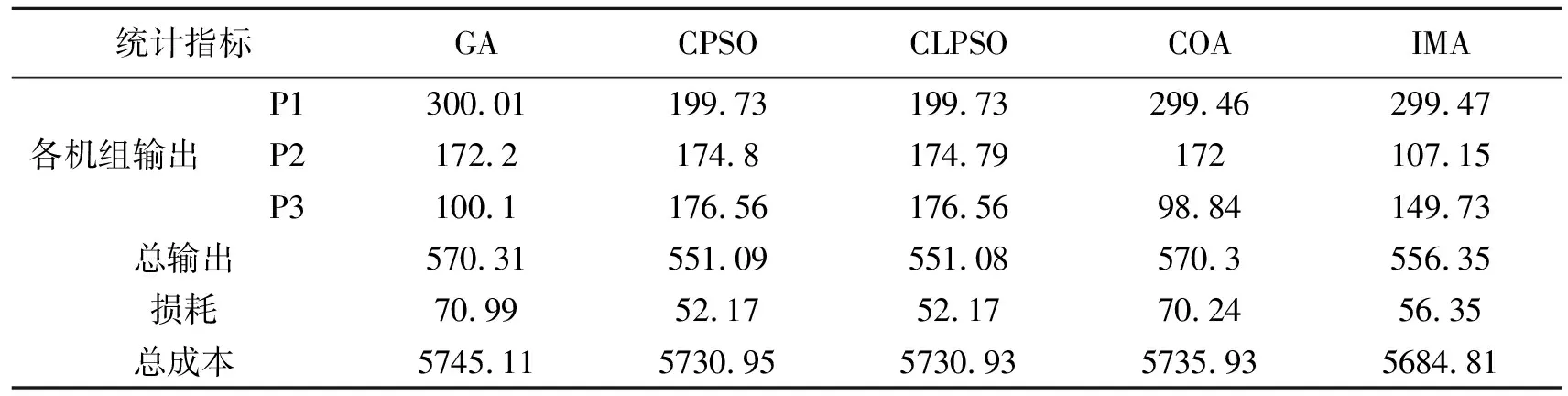
表5 三个机组电力系统的计算结果与对比

(二)六个机组的电力负荷分配问题求解

六个机组的电力负荷分配问题的总负荷为PD=1263 MW,各发电机的参数见表6所示。

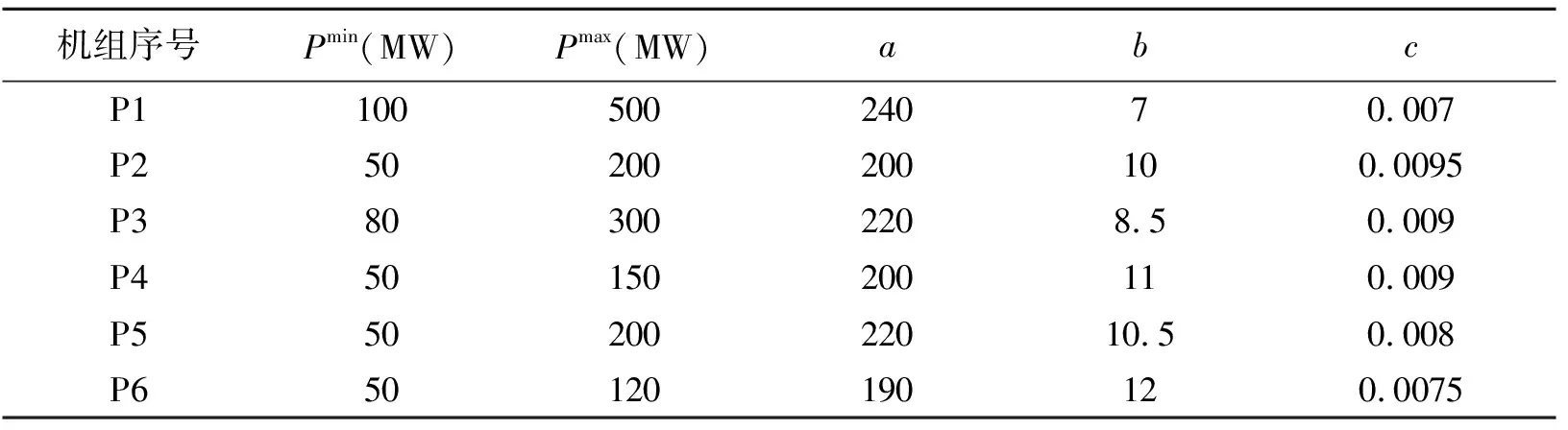
表6 六个发电机机组的参数

案例二中六个发电机机组的传输损耗系数矩阵为:

在案例二中,本文也分为只考虑电网传输损耗与和供需平衡约束和考虑电网传输损耗和阀点效应作为能耗函数计算总成本两种情形作为能耗函数计算总成本,借助IMA 算法求解该案例,并与遗传算法(GA)、粒子群优化算法(PSO)两种算法进行对比,种群规模为40,最大迭代次数为1000,三种算法在求解案例时独立运行30次,比较最差、平均和最好目标函数值,结果如表7所示。

表7 六个机组电力系统的最差、最好目标函数值

表8给出遗传算法(GA)、两种改进的粒子群优化算法(CPSO、CLPSO)、混沌优化算法(COA)以及改进的蜉蝣优化算法(IMA)五种算法求解六个机组的电力负荷分配问题的结果。结果对比可以发现的五种算法总能耗成本差别都不大,但表现最好的依旧IMA。再次证明蜉蝣优化算法求解电力负荷分配问题是可行和有效的。

表8 六个机组电力系统的计算结果与对比

(三)十五个机组的电力负荷分配问题求解

十五个机组的电力负荷分配问题的总负荷为PD=2500 MW,各发电机的参数如表9所示。

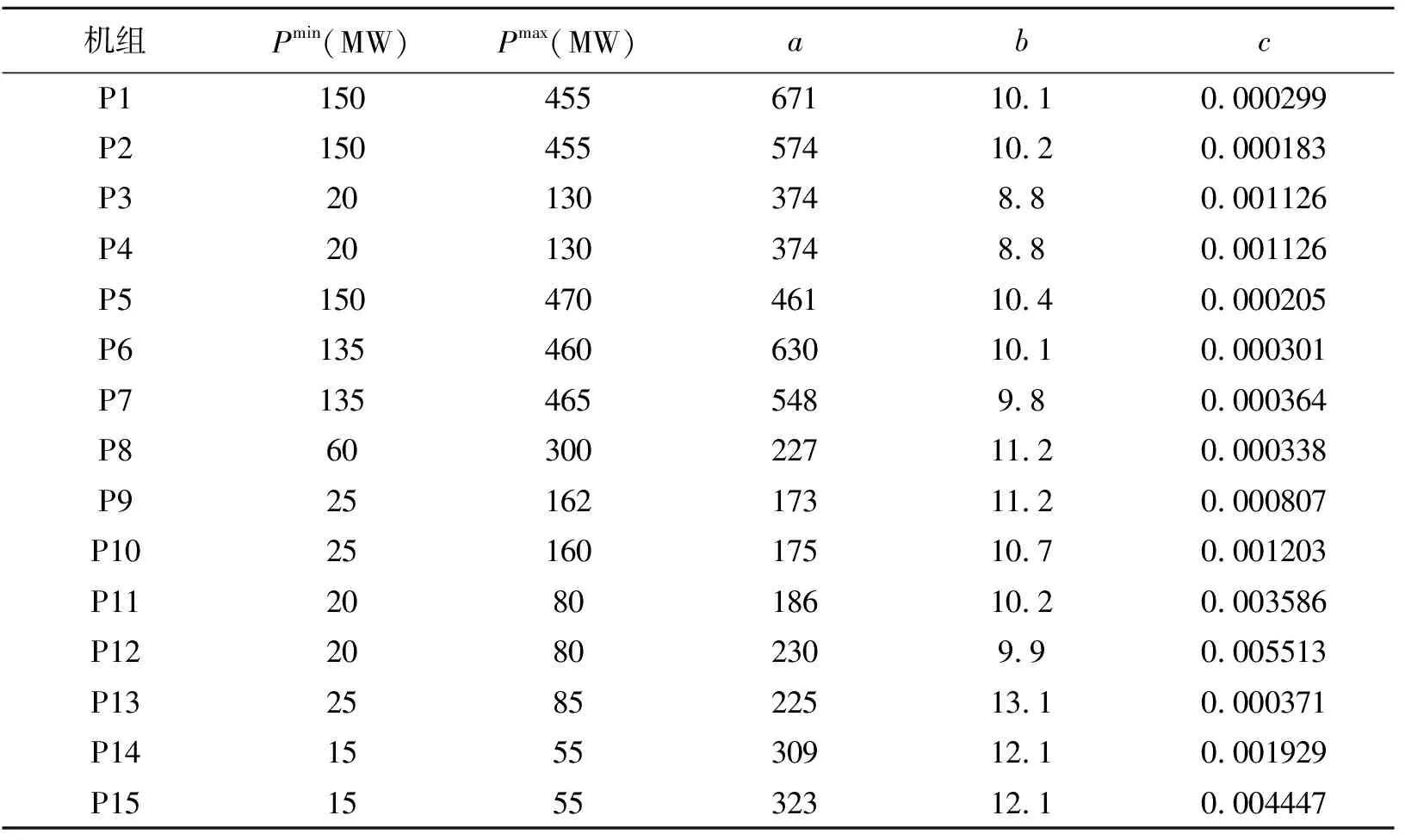
表9 十五个发电机机组的参数

在案例三中,本文与案例一、二相同,分为只考虑电网传输损耗与和供需平衡约束和考虑电网传输损耗和阀点效应作为能耗函数计算总成本两种情形作为能耗函数计算总成本,借助COA 算法求解该案例,并与遗传算法(GA)、粒子群优化算法(PSO )两种算法进行对比,种群规模为40,最大迭代次数为5000,三种算法在求解案例时独立运行30次,比较最差、平均和最好目标函数值,结果见表10所示。

表10 十五个机组电力系统的最差、最好目标函数值

从表11可以看出,运行结果显示五种算法求解 15 个机组的电力负荷分配问题所得到最优机组负荷分配及相应的总能耗成本差别都不大,其中IMA 表现最好,其次是GA和CPSO相差甚微,表现最差的是CLPSO。三个测试案例的实验结果表明蜉蝣优化算法在求解电力负荷分配问题中是可行和有效的,具有很强的稳定性,可解决电力系统中的能源消耗问题。

表11 十五个机组电力系统的计算结果与对比

五、结论

本文提出了一种基于精英策略改进的蜉蝣优化算法用于解决电力系统中的经济负荷分配问题(ELD)。该算法考虑了电网传输损耗、供需平衡约束和阀点效应,有效地处理了容量约束和电力供需平衡约束。实验结果表明,改进的蜉蝣优化算法在ELD问题上具有高效的求解能力,能够降低总发电成本和减少碳排放,取得了良好的应用效果。未来研究可进一步探索该算法在其他电力系统优化问题上的应用,并进一步提升其性能和适用性。