联合CTD、海底地形和ARGO数据构建北太平洋深海时变温度模型

张金辉,李姗姗,杨 光,范 雕,凌 晴

(1. 信息工程大学,河南 郑州 450000; 2. 华北水利水电大学,河南 郑州 450000; 3. 兰州理工大学,甘肃 兰州 730000)

海平面变化是全球气候变化的重要指示器[1-2],它受自然和人为因素共同影响。自工业革命以来,全球气候变暖直接导致海平面上升[3]。海平面上升不仅会反作用影响全球气候变化,还将直接威胁沿海区域的生态环境[4]和社会经济发展,甚至关乎沿海居民的生命与生存空间[2],以及低海拔岛屿的存亡[4]。

比容海平面变化作为海平面变化的重要组成部分,由于ARGO(array for real-time geostrophic oceanography)浮标目前仅能下潜到约2000 m 海深处,且在2005年之前浮标数目相对较少[2],因此大多数学者将研究时间选定为从2005年开始[5-14]。研究结果表明:2005-2015年全球海洋上层比容海平面上升趋势差异较小约为1.0 mm/a;但最近研究结果表明,2015-2019[15]或2020年[16],其上升速率分别达1.34和1.25 mm/a,表明近几年全球海洋上层比容海平面在加速上升[17]。

尽管2000 m以下海洋的温度变化相对较小,但却占整个海洋面积的50%[18],且2000 m以上海洋吸收的热量大约会有19%传导至2000 m以下的深海中[19],深海对比容海平面变化的贡献可能会较大[20]。由于当前深海温盐观测数据不足,对其比容海平面变化的研究也较少[4],一般利用卫星测高数据计算得到的全球平均海平面变化减去时变重力场和海洋上层ARGO数据估算的结果进行大致估计。笔者对文献[5-16]研究结果统计发现,即使在2005-2016年相同时间段其变化趋势差异也较大(0.23 ～0.56 mm/a),分析认为这主要与时间跨度、数据处理方法(如时变重力的低阶项处理、冰川均衡调整改正等[2])不同等因素有关,也反映出现今地球观测系统还不能完全捕捉到各因素对海平面变化的贡献[22]。当前,有学者开始尝试利用CTD数据模拟构建深海三维网格温度数据,由此直接估算出2005-2015年深海热比容海平面变化趋势为0.12±0.03 mm/a[4],其结果与文献[8,10,13]推算结果也存在较大差距。分析认为利用单个函数模型很可能不能准确地表达其所划分的全球各区域(特别是北太平洋)温度剖面随海深变化特征的差异性。此外,由于CTD数据具有低时空分辨率特点,若直接以各区域统计的温度剖面最值参与其所假设的比例关系运算,可能导致延伸推算的结果会产生较大偏差。

针对上述问题,本文选取北太平洋船测CTD数据,依据温度剖面随海深变化特性对该试验海域重新划分和建模,并联合海底地形和ARGO数据采用层层递推法构建北太平洋格网化深海时变温度模型,并对该模型数据的质量和反演的深海比容海平面变化进行评估和检验。

1 试验数据

1.1 全海深CTD数据

采用由国际全球海洋舰载水文调查项目整理并提供的高质量深海温盐剖面数据。该数据是利用测量船载着温盐深剖面仪大体沿着固定航线名义上每隔55 km测量一次,每次测量可获得从海洋表面到距离海底10～20 m深度上的每隔1或 2 m的温盐压等剖面数据[23]。由图1(a)可知,除P19航线外,其他航线均至少进行了一次全段或部分测段的重复测量,时间间隔最短仅1个月,最长可达37 a。为构建更可靠的模型数据,对其进行必要的质量再控制,以此作为构建深海格网化温度模型的基础和约束(如图1(b)所示)。

注:三角形用于区域划分,实心圆仅用于检核。图1 北太平洋CTD航线测量与分布情况

1.2 ARGO数据

采用中国ARGO实时资料中心发布的2005-01-2020-12格网化月均温盐数据,空间分辨率为1°×1°,垂直分层为0～2000 m不等间隔共58层。

此外,选取上述相同时间段由英国气象局最新发布的格网化月均温盐数据产品EN4.2.2(简称EN4),它相比于EN4.2.1的最大区别在于融合的数据源中由之前的全球海洋数据库13(wold ocean database 13, WOD13)改为WOD18。这里将EN4在海深2130～5350 m的12层温度数据作为参照进行比对。

1.3 海底地形数据

基于笔者所在院校提供的全球表面地形模型STO＿IEU2020[24]提取北太平洋海底深度。该模型是基于SIO V29.1重力异常和重力异常垂直梯度,并融合多源水深测量结果构建而成,其空间分辨率为1′×1′。为构建与ARGO数据空间分辨率相一致的深海温度模型,以ARGO格网点为中心,将该地形模型中经纬度相差1°范围内各点的平均海深作为该网格点的海底深度,并结合CTD航线实际分布提取北太平洋海深2000 m以下边界线(如图1(a)中黑实线所示)。

2 深海时变温度模型构建基础

2.1 CTD与ARGO数据温度剖面的一致性

CTD数据是一段时间内某条航线上的逐点测量值,而ARGO数据是经质量控制重构的格网化月平均值。为检验这两种数据的一致性,这里以ARGO数据格网点坐标为中心,在CTD航线上经纬度相差1°范围内海深大于1500 m各测量点的温盐剖面均值作为该点的温盐剖面数据,并与同年同月的ARGO数据进行比较,结果见表1。可知,在1000～2000 m,特别是1500～2000 m,两种数据的温度差异随海深增加逐步缩小,并趋于一致。据此推测,若ARGO计划未来可获取2000 m以下海洋温度剖面数据,则它与CTD测量结果也是一致的。

表1 北太平洋CTD与ARGO数据在海深1500～2000 m的温度差异 (℃)

2.2 深海CTD数据温度剖面的相对稳定性

由于CTD航线重复测量的时间间隔最长将近40年,受水团横向流动影响,2000 m以下温度剖面能否保持相对稳定是模拟构建深海温度剖面的基础。11条航线上首末两次测量的所有温度剖面,如图2所示。可以看出,尽管两次测量的时间间隔从15～37 年不等,但其温度剖面却保持较好的稳定性,这是因为CTD重复测量的时间间隔远小于深海水团循环周期(500～1600年)[25],因此可近似认为深海温度变化仅受深度方向上热量传递影响。此外,也可看出,各航线上首末两次温度剖面并非完全重合,如图2中的P02、P03、P10、P13、P16等,这是因为受当时海上测量各种海况因素影响,部分航线仅是对原航线的某段或对原航线进行了延长测量。

图2 北太平洋CTD航线首末两次测量的温度剖面

2.3 深海CTD数据温度剖面的波动性

为探究温盐深剖面仪能否测量出海深2000 m以下温度的微小变化[18],将这11条航线上首末两次各测量点坐标逐一比较,并视相距最近的两点为同一点,由此统计出北太平洋海深2000 m到海底温度剖面的波动情况,结果见表2。可以看出,北太平洋各层温度波动均随海深增加而减小,且各层温度波动的标准差均大于0.008℃(大于3倍的温盐深剖面仪测量精度0.002℃[23]),这表明北太平洋温度剖面的波动虽较小,但这种较小的波动却能被测定,而这种较小的波动正是构建深海时变温度模型的关键。

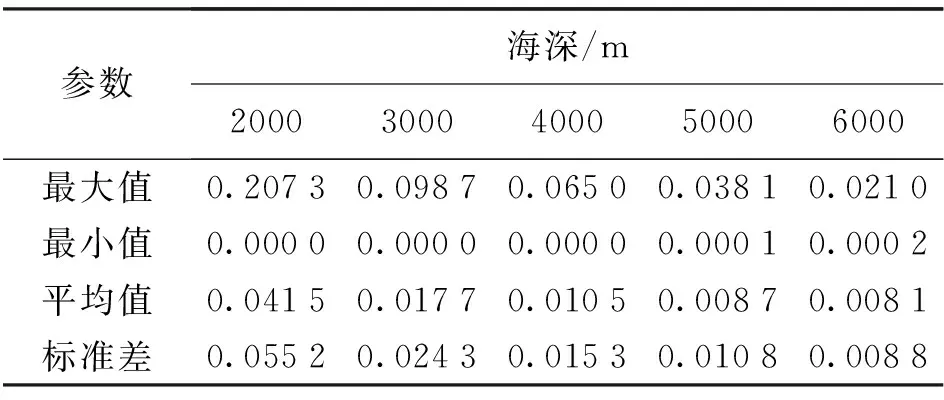
表2 北太平洋各层温度波动情况 (℃)

2.4 CTD数据2000 m以上深温度剖面的区域性

由图2可知,有些航线(如P01、P02)上测量点的温度剖面具有很好的相似性,但大部分航线(如P03、P14和P16等)的温度剖面则在某个界线两侧存在明显不同,即具有显著的区域特性。为合理划分温度区域,严格依据温度随海深变化特性,通过分析这14条全段测量航线(图1(a)中三角形所示)上测量点的温度剖面,并与不同航线上温度剖面相互比较,由此确定出不同温度区域间的分界点,然后将分界点连接,由此划分为11个区域(如图3所示),与文献[4,26-28]在北太平洋的划分结果完全不同。此外,从区域划分结果来看,在空间上与大洋洋流存在一定联系,如黑潮位于区域①,千岛寒流位于区域③,加利福尼亚寒流位于区域⑨,其他区域则与赤道逆流或北赤道暖流有很大重合,这说明由于大洋洋流的性质不尽相同,在其循环流动过程中很可能对原海水温度剖面特性产生了一定影响。

图3 依据温度随海深变化特性划分的北太平洋温度区域

为检验上述区域划分是否合理,将各区域内每条航线(图1(b)中圆形所示航线)上的温度剖面逐一地与同一区域内所有参与区域划分航线上的温度剖面进行比较,结果如图4所示(P04和P19在区域10、11内均未重复观测,括号中的内容为该航线标识)。可以看出,各区域内温度剖面吻合度很好,且不同区域温度剖面的差异性也较明显,这说明上述温度区域划分是比较合理的。

图4 北太平洋温度区域检核

3 北太平洋深海时变温度模型的构建与检验

由于深海温度剖面具有相对稳定性,且随时间变化又具有一定的波动性,显然这种波动应该是各点的温度剖面围绕均值在一定范围内变化。为此,基于各区域内CTD数据构建一段时间内深海温度剖面均值与最值数学模型模拟其随海深变化的特性和波动范围,这里以构建温度剖面均值模型为例,最值模型构建与之相同。

3.1 温度剖面均值数学模型的构建与检验

为构建各区域1500 m以下温度剖面均值模型,基于各区域内所有航线(图1(b)中实心圆表示的航线除外)得到各层温度剖面的平均值,如图5所示。可以看出,各区域温度剖面均值线的差异性较明显,即表现出较明显的区域特性;此外,也可看出,除区域在3000 m以下温度随海深增加呈现线性趋势性特点外,在3000 m以上部分与其他区域的温度随海深增加先下降再缓慢上升的变化特性相似。除区域在3000 m以下采用线性函数模型,其他则采用如下数学模型进行拟合,公式为

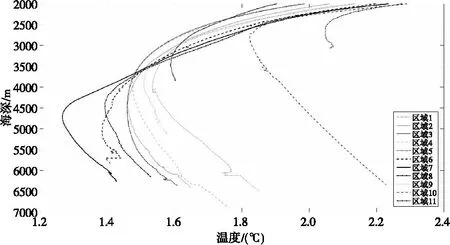
图5 北太平洋各温度区域CTD温度剖面均值线

T′i(h)=ai+bi×h+ci×hdi+ei×logh

(1)

式中,T′i表示温度区域;i表示区域编号;h表示从1500 m到海底H之间的海深;ai、bi、ci、di、ei为各区域温度剖面均值模型的待定系数。

为确定上述区域温度剖面均值模型中的参数,基于最小二乘估值准则(VTV=min)解算,结果见表3。从参数拟合结果来看,各区域温度剖面均值虽可归结为统一的数学模型,但各区域具体数学表达式区分度较大,这也表明温度随海深变化的区域性是较显著的。

表3 北太平洋各区域温度剖面均值数学模型参数

图6 北太平洋温度数学模型拟合结果与CTD实测温度剖面比较

3.2 北太平洋深海时变温度模型构建与检验

测量点的温度剖面可视为随时间变化围绕均值在最值之间波动,由于2000 m以下ARGO与CTD数据的测量结果在理论上具有一致性,为此以各区域温度最值模型相对于均值模型的波动大小,借助于海底地形将ARGO数据推算延伸至海底。为便于说明以区域④为例,其他区域的推算方法与之相同。

3.2.1 模型构建方法

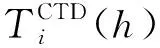
图7 将2000 m以上ARGO温度剖面延伸至海底的原理

(2)

(3)

式中,H表示海底深度;ai表示各区域内在海深2000 m(含)以下ARGO网格点的温度剖面值(海深2000 m时)或推算值与均值模型T′i(h)的差异,其计算表达式为ai(λm,φn,h,tk)=Ti(λm,φn,h,tk)-T′i(h)h≥2000 m。式中,bi表示各区域内在海深2000 m(含)以下最大值模型T′iR(h)与均值模型T′i(h)的差异,其计算表达式为

式中,di(h)表示推算相邻层所在海深的最大值模型T′iR(h)与均值模型T′i(h)的差异,其计算表达式为

di(λm,φn,h+Δh,tk)=T′iR(h+Δh)-

T′i(h+Δh)h≥2000 m

当将2005-2020年北太平洋ARGO所有网格点月均温度数据均延伸至海底后,即构建了与ARGO数据具有相同的时空分辨率的北太平洋深海温度模型。

3.2.2 模型数据检验

为检验该温度时变模型数据的质量,将其与图1(b)中用于模型检核(实心圆所示)的7条航线进行比较,以ARGO数据格网点坐标为中心,将航线上经纬度相差1°范围内各测量点的温度剖面均值作为该格网点的实测温度剖面数据,并与同年同月的模型数据进行比较,统计结果见表4。可以看出,在北太平洋海深2000 m以下,模型数据与CTD数据在温度上的最大差异不超过0.20℃,平均差异不超过0.03℃,标准差不超过0.06℃。这表明本文构建的温度模型数据与CTD实测结果较接近,结果较可靠。

表4 北太平洋温度模型数据与CTD实测数据差异

此外,还将该温度模型数据与EN4在海深2130～5350 m的12层温度数据比较,统计结果见表5。可以看出,在北太平洋海深2000 m以下,模型数据与EN4数据间的温度差异随海深增加而增大,但最大差异不超过0.54℃,平均差异不超过0.42℃,标准差不超过0.002℃。分析认为,由于EN4以气候态作为背景场采用最优插值法进行数据校正和重构,而本文则是以低时空分辨率的CTD数据作为基础和约束采用层层递推法分区域重构,这是造成两类数据存在一定差异的主要原因。

表5 北太平洋温度模型数据与EN4数据差异

为检验温度模型数据解译深海比容海平面变化能力,计算该模型与EN4在2005-2020年北太平洋深海比容海平面变化时间序列(其相关系数为0.708 6),如图8所示。可以看出,该模型与EN4的深海比容海平面变化时间序列整体符合性较好,如在2005-2010年,模型数据与EN4在北太平洋深海比容海平面均存在较明显的上升趋势(前者为0.52±0.09 mm/a,后者为0.73±0.11 mm/a),这与文献[28]基于海洋热含量(ocean heat content, OHC)所得到的从2000-2010年整个太平洋也存在较为明显的增温趋势的结论一致;此外,也可看出,在2010年之后,EN4出现小幅震荡,即深海比容海平面变化时间序列先下降再上升,然后基本保持不变,而模型数据的深海比容海平面变化时间序列则几乎一直保持不变,虽然两数据的时间序列存在一定差异,但在2010年之后它们在整体上均没有表现出明显的上升趋势(前者为0.02±0.03 mm/a,后者为-0.01±0.01 mm/a),这与文献[29]通过延长文献[27]的数据发现在2010年之后太平洋的热含量变化较为微弱也不存在明显的增温趋势的结论一致。此外,在整个研究时间段内,模型数据与EN4在北太平洋2000 m以下比容海平面的上升趋势分别为0.11±0.17和0.09±0.11 mm/a,计算结果基本一致,说明该模型数据可以较好地反映北太平洋深海比容海平面变化趋势,所构建的时变模型数据具有一定的可靠性。

图8 北太平洋2000 m以下比容海平面变化时间序列

4 结 论

针对深海温度实测数据不足的现实情况,本文首先依据CTD温度剖面随海深变化特性重新对北太平洋海域进行了区域划分和分区域建模;然后基于各区域的温度剖面均值和最值模型,联合海底地形和ARGO数据采用层层递推法构建了2005-2020年北太平洋深海月均格网化温度模型,并反演了其深海比容海平面变化,试验结果表明:

(1)本文构建的深海温度剖面均值数学模型相较于文献[4]提出的数学模型与CTD实测温度剖面均值的差异要小1～2个数量级,更能准确地反映各区域深海温度剖面随海深变化特性,且在表达形式上更为简洁。

(2)本文构建的2005-2020年北太平洋深海月均格网温度模型与CTD数据的最大差异不超过0.20℃,平均差异不超过0.03℃,标准差不超过0.06℃,与EN4数据的最大差异不超过0.60℃,平均差异不超过0.50℃,标准差不超过0.002℃,表明该模型与CTD数据和EN4具有较好吻合度。

(3)在2005-2010年,基于本文构建的温度模型和EN4计算得到的北太平洋深海比容海平面均存在较为明显的上升趋势(前者为0.52±0.09 mm/a,后者为0.73±0.11 mm/a),而在2010年之后没有表现出明显的上升趋势(前者为0.02±0.03 mm/a,后者为-0.01±0.01 mm/a);在整个研究时间段内,两者的比容海平面的上升趋势分别为0.11±0.17 和0.09±0.11 mm/a,这说明本文构建的温度模型数据具有一定的可靠性,能够较好地反映北太平洋深海比容海平面变化趋势,这对于闭合区域海平面平衡方程成因变化的解释具有一定的参考价值。