基于EMD 和复杂度的期货市场农产品交易额分析

韩清滨

（沈阳化工大学马克思主义学院，辽宁 沈阳 110142）

农产品市场是一个极其复杂的非线性动力学系统。由于各种因素的互相作用，使得农产品市场的运行规律难以准确描述， 其中农产品期货一直是人们研究与关注的热点［1］。 高效全面地分析农产品期货交易，为国家农产品生产、储备、贸易提供一定的参考依据， 对保障农产品有效供给以及市场稳定均具有重要科学意义。

文章采用的样本数据为大连商品交易所与郑州商品交易所农产品近5 年交易额， 农产品期货交易额具有多变量强耦合、非线性、参数时变的特点。 被分析的农产品期货交易额数据通常是非平稳的、非线性的［2］。 基于非线性的分析方法与手段如复杂度、近似熵等对非平稳信号的分析更为方便、高效［3］。 非线性信息混杂在大量的随机噪声之中，因此，对信号进行辨识，将有用信号提取出来也非常复杂。经验模态分解方法（Empirical Mode Decomposition Method，EMD）是一种高效的时间序列分析手段［4-5］。 本文利用经验模态分析方法（EMD）将大商和郑商的农产品期货交易额进行经验模态分析。 首先进行去除随机信号噪声干扰， 并获得基本模式分量（Intrinsic Mode Function，IMF）， 然后从去噪信号中提取有效IMF，再计算IMF 的复杂度来进行对比研究。

复杂度作为非线性的分析指标， 其物理意义可以看作时间序列里面序列长度增加过程中出现新的模式的概率与速度， 可以作为描述系统变化的一个有用参数， 因此复杂度广泛应用于生物医学信号的识别、随机信号以及其他领域［6-7］。 复杂度对于系统的状态演变有非常灵敏的反应， 因此可以使用复杂度对两大交易所的农产品期货交易额变化规律进行表征。 本文以近5 年内大商和郑商期货农产品交易额为研究对象，选择交易额进行分析，应用经验模态方法与复杂度相结合的方法， 由此对我国农产品期货交易的复杂性展开讨论并作深入分析研究。

1 经验模态分解理论

固有模式分量IMF 的概念是由美籍华人Norden E . Huang 等人在1998 年提出的。 经验模态分解EMD 理论就是把非平稳信号进行逐层分解，每一层信号就是有实际物理意义的瞬时频率IMF分量，获得IMF 可以看作是一种新的自适应信号分解方式， 由此提高了非线性、 非平稳信号分析的效率。

EMD 分解步骤如下：

（1）对原始信号x（t）分别迭代加入N 次平均值为0，其幅值的标准差是常值的白噪声ni（t），可得信号xi（t）（i=1，2，3，…，N）：

（2）对xi（t）进行经验模态分解，分解得到多个瞬时频率IMF 分量以及余项ri（t）：

在这里cij（t）为第i 次加入白噪声后，得到的第j 个瞬时频率分量，其中j=1，2，3，…，K。

（3）随后根据不相关随机理论中的统计序列值的平均值等于0 的要求，对上述一一对应的IMF 值进行进一步的平均求和计算， 得到了经验模态分解的瞬时频率分量和残差r（t）：

其中，cj（t）是原始信号进行EMD 分解后的第j 个IMF。 最终得到K 个IMF 分量和一个余项：

待分析时间序列即原始信号经过经验模态分解后可以得到的瞬时频率分量。 这些IMF 分量中只有少数信息是有用的，因此还需进一步筛选，由此可以得出待分析数据的有效分量。

2 复杂度算法

复杂度是由20 世纪的Kolmogorov 等人给出的定义，如下：系统的行为即一个系统在空间的结构组成以及随着时间流逝而带来的演变， 由此决定了系统的复杂程度，但是Kolmogorov 并没有给出详细的计算过程。直到十年后由A. Lempel 和J. Ziv 给出更加简单的复杂度计算算法，也就是Lempel-Ziv 复杂度，此后复杂度作为计算分析时间序列中非常重要的非线性指标而得到人们的广泛关注与研究应用。

Lempel-Ziv 复杂度的算法如下：

式中，x=（x1，x2，…，xn）/n。

令S=（s1，s2，…，sr），r＜n，Q=sr+1，形成SQ 字符串。

将“o”前的所有字符看作S，重复上述步骤。 例如，对于序列｛0.1，0.2，0.3，0.4｝，重构得到其“0.1”序列“0011”。

字符串被“o”分成段的数目即为该序列的复杂度C（n），显然上例中C（4）=3。

据A. Lempel 和J. Ziv 的研究，几乎所有0、1 随机序列的复杂度都趋于B（n）=n/logn，则可得相对复杂度R（n）=C（n）/B（n），它反映一个序列与随机序列的接近程度。

由上面的分析可知， 使用复杂度可以得出时间序列在随着长度增大的时候可以产生新的模式的速度，可以这么说待研究的时间序列的复杂度越复杂，待研究时间序列的变化随之变化越大，由此而产生新的变化的趋势也就变得越快，可以推出此时间序列是无序的，反之亦然。 通过上面的分析可得复杂度参数是可以表征时间序列的非线性特征的假设及其合理性的阐述，是对分析方法的说明。

3 大连和郑州期货商品交易所的农产品交易额分析

图1 所示为近5 年大商和郑商农产品期货交易额的时域分析示意图， 图中曲线是以交易日交易数额构建的数据序列。从图1 可知，交易所农产品交易额有所不同， 时间序列呈现随时间变化的非平稳特征。 从图1 中很难表征这两个时间序列的区别。

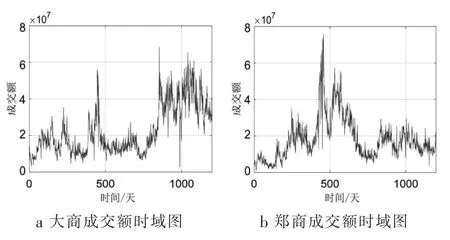
图1 大连和郑州期货交易所农产品期货交易额

为了进一步对大连和郑州期货交易所农产品期货交易额进行区分，采用前文所提到的方法进行处理计算，首先进行交易额非线性定性分析。

3.1 农产品期货交易非线性分析

首先对两大交易所农产品期货交易额进行初步的非线性定性分析与比较。 利用MATLAB 计算出近5 年两大交易所的农产品期货交易额的散点图。

散点图是农产品交易额时间序列的峰值集合。考虑采样误差的因素，在散点图中农产品交易额的时间序列的周期点会积聚在一个小的区域范围之内。 由图2 可知两大交易所的交易额的散点图里出现了分散的点的区域，根据非线性理论可知，由交易额组成的间序列存在着不规则的或者存在奇怪吸引子。 从近5 年农产品的成交额的散点图看出这两者之间是有区别的，但是只能定性描述，而不能定量化表征。

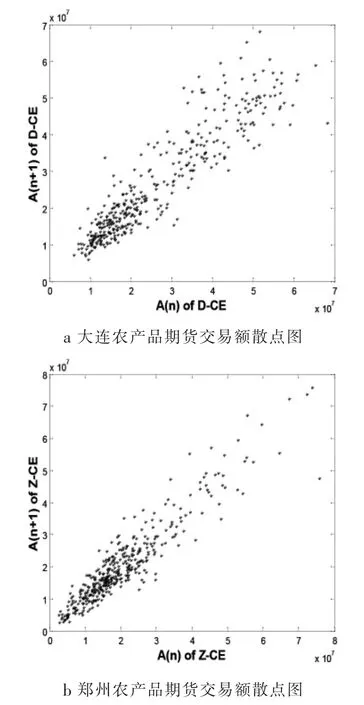
图2 大连和郑州交易所农产品期货交易额散点图

3.2 农产品期货交易非线性分析：对大连和郑州期货交易所农产品期货交易额进行EMD 分析

为了消除噪声对信号内部本质特征的影响，对大连和郑州期货交易所农产品期货交易额进行EMD 分解，分解结果如图3 所示。

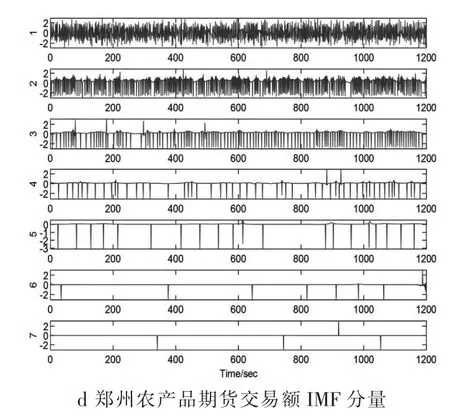
图3 不同交易所农产品期货交易额EMD 分解与其IMF 分量

对两大交易所农产品期货交易额的经验模态分解结果如图3 所示。

对上图进行分析，从图3 中可以清晰看出，大连期货交易所农产品近5 年的期货交易额经过经验模态分解后， 得到了6 个IMF 分量以及残余分量，郑州期货交易所农产品近5 年的期货交易额经过经验模态分解后得到了7 个IMF 分量以及残余分量。 为进一步分析两大交易所农产品交易额的非线性特征，对IMF 分量进行复杂度分析。

3.3 第1 层IMF 复杂度分析

经过EMD 分解后的信号拥有众多的本征模态分量，对IMF 进行筛选，选取两个期货交易所农产品期货交易额的第1 层IMF 进行复杂度分析。

由前文可知单一随机噪声下的复杂度经过归一化计算后，其值接近1，由此引起的时间序列的复杂度计算值会偏大。为了消除此影响，使用经验模态分析（EMD）找到最能代表时间序列的信号成分，由此消除噪声的影响。 本文基于经验模态与复杂度相结合的方式对两个期货交易所农产品交易额进行分析的过程如下所示：

（1） 首先计算两个交易所近5 年内交易额的经验模态分解，得到一组IMF 分离，如前所示。

（2） 分别计算复杂度归一化值CnNH和CnNL，再综合得到最终指标CnNF，称之为复杂度综合指标。

经验模态分解可以理解为主成分分离方法，也就是要将时间序列中蕴含的重要的、 有用的信息提取出来，据文献［4-5］可知两个期货交易所农产品期货交易额的主要成分集中在前1 个IMF 中，且越靠上层的IMF 分量具有的能量越高， 具有较高的信噪比，所以，本文提取第1 层的IMF，以第1 层的瞬时频率IMF 为分析对象，计算其复杂度，分析结果如图4、表1 所示。

表1 两大交易所农产品期货交易额第1 层IMF 复杂度比较

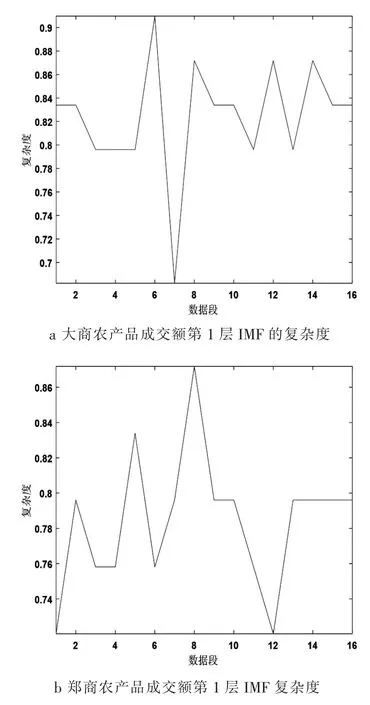
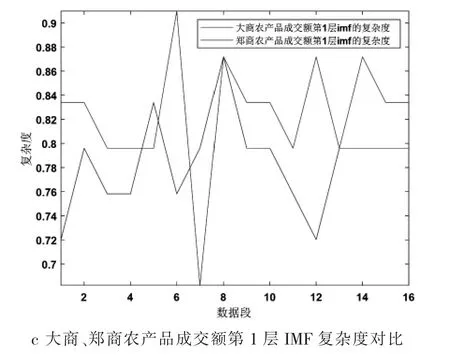
图4 交易所农产品近5 年交易额第1 层IMF 的复杂度

如图4，由IMF 复杂度折线图可以看出，由于第1 层IMF 具有较高的能量与信噪比， 复杂度对比比较明显，可以清楚地看到，大连和郑州期货商品交易所的农产品交易额的复杂度可以很好地区分大连和郑州期货商品交易所的农产品交易额变化趋势。

表1 比较了两大交易所近5 年的农产品期货交易额第1 层瞬时频率IMF 的复杂度值。 由此可见，第1 层IMF 的复杂度值对于识别大连和郑州期货商品交易所的农产品交易额具有一定的实际意义。

4 结语

文章结合了经验模态方法和复杂度分析方法对近5 年的大商和郑商交易所农产品期货交易额进行了详细的定性比较与定量分析。对于这两组交易额，它们的散点图在形貌上还是有区别的。 经验模态分解方法和复杂度分析能够更加准确细致地展现出了大连和郑州期货商品交易所的农产品交易额变化规律的非线性动力学特性， 对于两大交易所的农产品交易额， 经验模态分解与复杂度相结合相较于传统的时域分析方法，具有高区分度、更直观、更准确的特点， 能够定量识别出大连和郑州期货商品交易所的农产品交易额的非线性特征。 为揭示农产品复杂的供需变化特征、 促进农产品市场调控科学性和可预见性，提供了新思路、新方法。