深水井口导管管土界面摩擦退化试验研究
刘书杰, 何 连, 刘 正, 包兴先, 王 腾
深水井口导管管土界面摩擦退化试验研究
刘书杰1, 何 连1, 刘 正1, 包兴先2, 王 腾2
(1. 中海石油(中国)有限公司海南分公司, 海南 海口 570312; 2. 中国石油大学(华东)石油工程学院, 山东 青岛 266580)
深水井口导管在黏土中的贯入阻力与导管土体界面的黏性摩擦系数密切相关。在导管安装过程中, 管土界面会产生大位移剪切, 使得导管-黏土界面剪切力产生退化。本文针对传统剪切试验装置小位移剪切的限制, 无法正确描述井口导管贯入时导管-黏土界面大位移剪切时的退化机理, 采用GDS多功能界面剪切试验仪在恒应力条件下进行大位移单调剪切试验, 研究法向应力对导管管土界面摩擦退化机理的影响规律。试验结果表明, 大位移单调剪切时, 界面剪应力随剪切位移先增大后减小, 最终趋于稳定, 界面表现出剪应力退化现象, 随着法向应力的增大界面峰值应力与残余应力均增大; 土样法向位移随着剪切位移、法向应力的增加而增大最终趋于稳定。最后在对试验数据分析的基础上, 基于剪应力随无量纲位移的退化规律, 提出了界面剪应力随累积位移退化的计算方法。并结合算例对比分析了井口导管在贯入80 m深度处, 由于界面摩擦退化效应导致导管贯入阻力降低了28.48%。
导管; 贯入阻力; 黏性界面; 摩擦退化; 界面剪切试验
水下井口导管是井身结构中的第一层表层套管, 它为整个导管柱、海底采油树和防喷器组提供结构和支撑。目前, 在深水环境中把喷射下导管技术当作首选的导管安装方法[1-2]。简单来说, 如图1所示, 整个喷射管串系统由内外两层管柱组成, 内层管柱主要包括底部钻具组合、钻柱等, 外层管柱为导管。管串送达海底泥线时, 钻头边旋转边喷射钻孔, 管串依靠自身的重力克服土体摩擦阻力, 保证导管顺利贯入。在导管贯入过程中, 如果设计的管串重量过大, 导管下至预定深度时, 松开大钩后, 由于管土之间的侧摩阻力过小, 导致井口失稳并下沉。如果设计的管串重量过小, 在安装过程中会出现卡钻现象, 导管无法下至预定深度[3]。因此, 需要正确评估导管贯入过程中的阻力变化, 合理配置管串重量, 保证导管下入到设计深度。
由于导管的贯入安装过程和桩基贯入过程相似, 因此, 通常参考桩基贯入阻力变化来研究导管贯入阻力。在不排水情况下, 美国石油协会(American Petroleum Institute, API)规范[4]建议黏土中管土界面的剪应力是当前土体强度u的函数, 即:
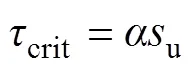
式中, α是界面的黏聚力系数, 取值范围从0到1, su是土体的不排水抗剪强度[4]。
对于桩基贯入过程中黏性界面的摩擦退化现象, 帝国理工学院法、Fugro法、西澳大学法推荐通过引入(/R), 来考虑桩基贯入黏土中桩侧阻力退化, 其中为土体离桩端的距离,为桩的半径,为退化系数[4-7]。在导管贯入过程中, 管土之间存在较大的相对位移, 管身单位侧摩阻力也会出现不同程度的退化, 即管土界面处会出现的剪切退化效应[8]。管土之间的侧摩阻力达到极限后会出现退化, 最终衰减到一个定值, 对应的桩土界面的黏聚力系数α通常为土体的灵敏度t的倒数[9-11], 而Akers等人[12]通过现场试验得出导管的单位侧摩阻力通常取未扰动土体的不排水抗剪强度的1/4~1/3, 近似达到该区域土体的灵敏度的倒数(t=2.6~3.6)。
许多学者对桩-土界面剪切特性及其影响因素进行了大量试验研究, 但桩-黏土界面力学特性的试验较少[13-23]。通过界面剪切试验发现界面力学特性不仅取决于界面材料及其粗糙度, 还取决于土体的成分、含水量、法向应力的大小和剪切速率[14, 19-20]。Taha等[21]通过环剪仪进行了恒应力的黏土界面剪切试验, 结果表明界面剪应力在剪切位移为2~3 mm时达到峰值, 后由于土体颗粒重新定向排列界面剪应力出现退化, 当剪切位移为100 mm时达到残余抗剪强度; 且在剪切过程中试样体积减小, 发生剪缩现象。
由于传统界面剪切试验装置的限制, 研究成果主要为小位移界面剪切, 且单调界面剪切试验的剪切位移在8 mm左右。缺少大位移作用下的界面剪切机理研究。本文针对井口导管-黏土界面进行大位移作用下的单调剪切试验, 研究其对界面摩擦阻力退化机理, 合理地确定导管贯入过程中的贯入阻力, 以保证导管在实际安装过程中顺利贯入这一工程问题。
1 试验设备及试验方案
1.1 试验设备
试验所用仪器为多功能界面剪切试验仪, 试验仪由英国Global Digital Systems (GDS)公司生产, 如图2所示。钢板剪切面固定转动约束, 旋转底盘带动土样转动, 实现土样与钢板剪切面的连续剪切。试验过程中, 实时测试扭矩、法向荷载、竖向位移和转动角度(位移)。
土样剪切过程中面积不变, 通过测试剪切过程中的扭矩, 由式(2)得到界面的平均剪切应力:
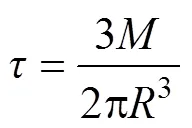
式中,为界面剪应力, 单位kPa;为扭矩, 单位(N·m);为剪切面的半径, 单位m。
1.2 试样准备及试验方案
试验用土为高岭土, 首先使用烤箱将黏土块烘干, 将干燥后的黏土块粉碎并使用粉磨机磨成粉, 然后使用0.03 mm的筛子进行筛分。再将黏土粉末与蒸馏水混合, 得到含水量80%的黏土泥浆。将黏土泥浆缓慢放入固结仪中, 对土体施加法向应力与反压, 使土体在有效法向应力为200、250、400 kPa的情况下完全固结。

图2 GDS多功能界面剪切试验仪
采用GDS多功能界面剪切试验仪开展恒定法向应力下剪切速率为1 cm/min的界面单调剪切试验, 以研究法向应力、剪切位移对界面剪切性能的影响。试样尺寸为直径70 mm, 高22 mm, 试验方案如表1所示。
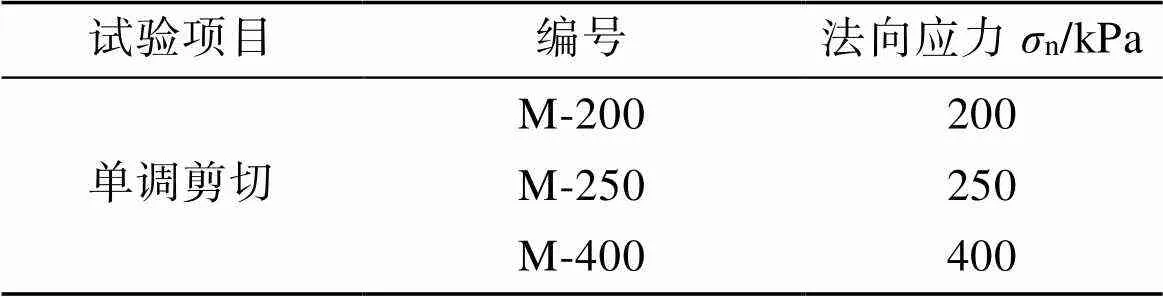
表1 界面剪切试验方案
2 试验结果与分析
图3为不同法向应力下钢-黏土界面剪应力-剪切位移曲线。从图中可以看出, 不同法向应力下钢-黏土界面剪应力都随着剪切位移的增加而逐渐增大, 在2 mm剪切位移时达到峰值, 后随位移增大减小并趋于稳定, 即出现应力软化现象。且当变形超过一定值后, 则处于相对稳定状态。且随着法向应力的增大, 钢-黏土界面的界面峰值抗剪强度和残余抗剪强度增大。本文根据试验数据, 拟合出界面峰值抗剪强度与土体初始不排水强度ui的关系如式(3)所示(2=0.987); 残余抗剪强度与土体强度的关系如式(4)所示(2=0.994)。
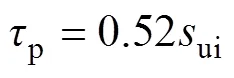
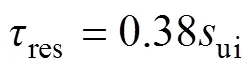
本试验中假定界面黏聚力系数不变, 则可求得土体单调剪切至稳定的灵敏度等于相同法向应力下峰值强度除以残余强度。由此可知, 当法向应力分别为200、250、400 kPa时, 灵敏度为1.27、1.33、1.41, 由此可知随着法向应力的增大土体灵敏度增大, 桩-黏土界面的退化程度增大。
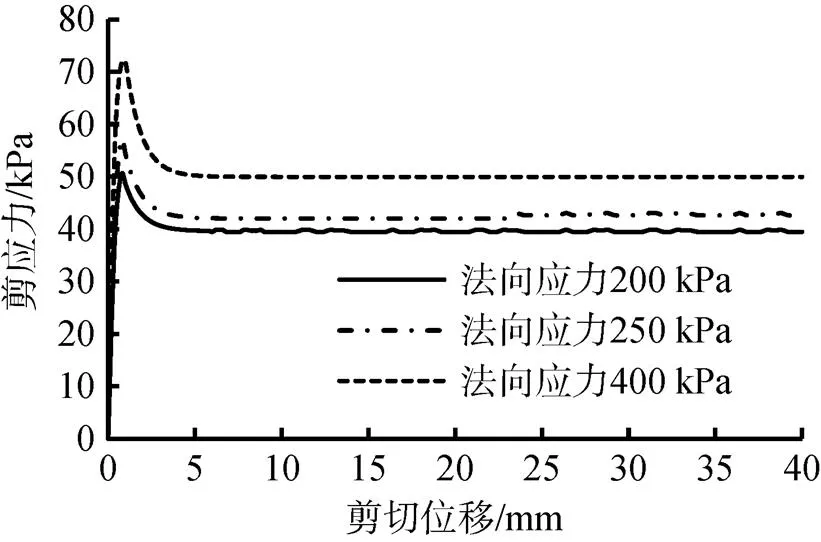
图3 剪切应力-剪切位移曲线
图4为不同法向应力下钢-黏土界面法向位移-剪切位移曲线。由图4可知, 在不同法向应力下, 界面剪切试验过程中试样发生了剪缩现象, 这是由于土体颗粒的重新定向排列产生的。从界面剪切位移-法向位移曲线可以看出, 试样剪缩大部分发生在0~ 10 mm剪切位移范围内, 占总剪缩量的90.1%; 当剪切位移在10~40 mm范围内时, 试样剪缩现象呈现退化趋势, 且试样总的体积形变最终达到一个稳定值, 这与孔令伟[20]做的试验结果基本一致。
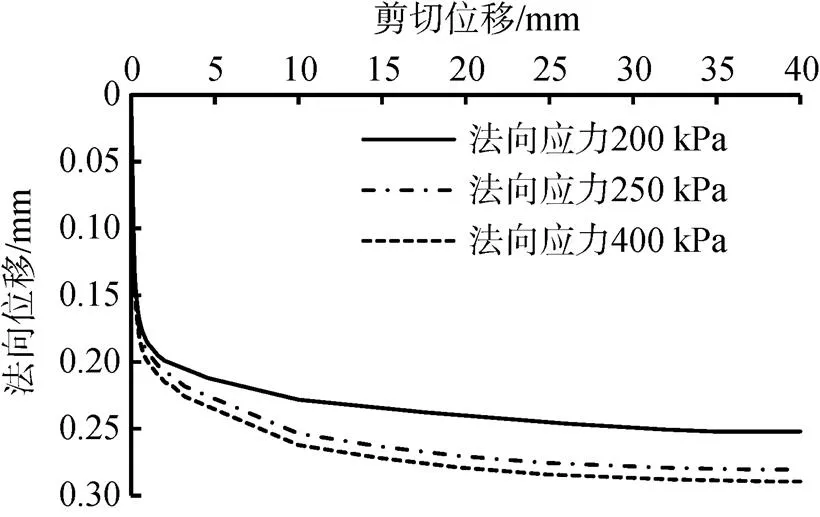
图4 法向位移-剪切位移曲线
3 界面摩擦退化机理研究
表2给出了不同法向应力下的界面的黏聚力系数、ui与残余剪切强度。由表2可以拟合ui=0.396v。为研究界面强度退化规律, 这里假定黏聚力系数不变, 则界面剪应力退化即为土体强度的退化。
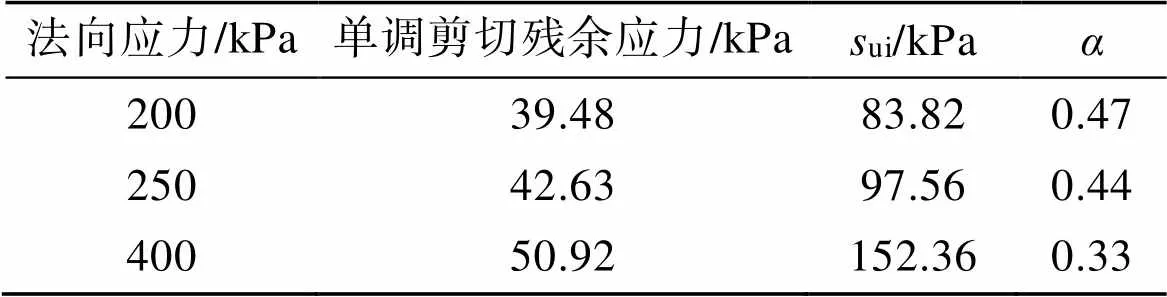
表2 不同法向应力下的界面的黏聚力系数与土体强度
Einav等[22]基于循环T-bar试验, 通过累积塑性应变建立土体强度循环退化模型, 即
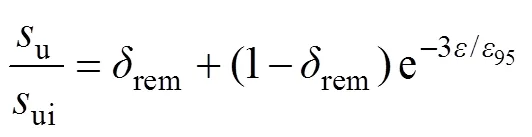
式中,u为土体当前不排水抗剪强度, 单位kPa;ui为土体初始不排水抗剪强度, 单位kPa;rem为土体灵敏度t的倒数, 单位无量纲;为累积塑性应变, 单位无量纲;95为土体发生95%重塑时累积塑性应变, 单位无量纲。Wang等[23]提出了土体强度随累积位移循环退化的计算公式,
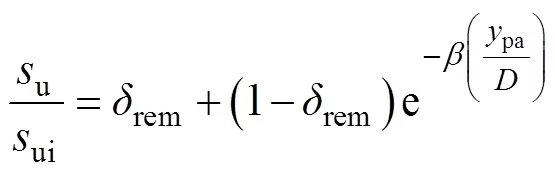
式中,pa为土体的剪切位移, 单位m;为衰减系数, 无量纲;为桩径, 单位m。从式(6)可以得知, 当剪切位移pa增大到一定程度后,u/ui=rem。因此rem控制土体退化后的稳态强度。
本文以式(6)为基础, 定义了剪切位移和法向应力相关的无量纲位移参数pa/10050, 并对试验数据拟合, 建立了基于无量纲累积位移的界面剪应力退化公式, 即
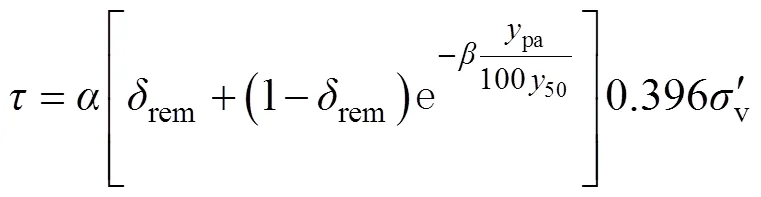
式中,为界面黏聚力系数, 单位无量纲;为衰减系数, 单位无量纲;50为达到峰值剪应力一半时对应的剪切位移见表3, 单位m。

表3 y50的数值
式(7)中的rem可以直接由剪切过程的u/ui求得。衰减系数可通过式(7)拟合图3中曲线得到, 拟合衰减系数见表4。表4中拟合的复相关系数2均大于0.995, 且不同法向应力条件下界面剪应力衰减系数均为0.2, 表明衰减系数与剪切位移幅值、法向应力无关, 即无量纲位移能合理反映法向应力和剪切位移幅值的综合影响。
将拟合得到的=0.2代入到式(7)可以计算得到大位移剪切荷载作用下的界面剪应力。式(7)中的参数可由API规范[4]确定, 式(7)可以计算桩基在大位移剪切作用下的桩侧摩阻力的退化特性。
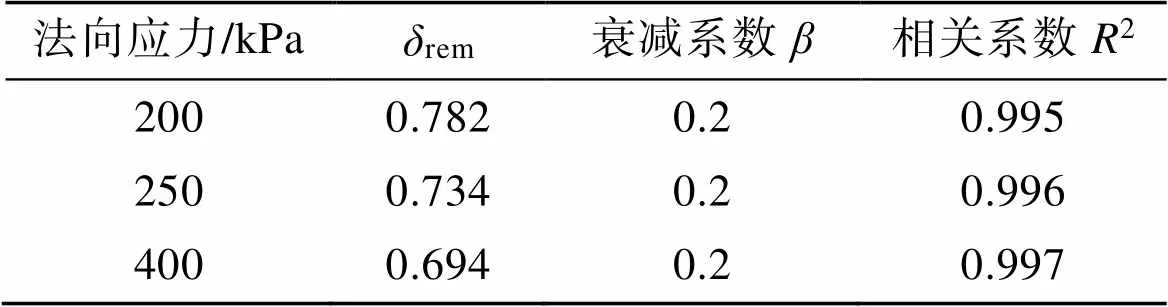
表4 拟合曲线求得参数
4 算例分析
为了研究黏性界面退化模型对导管贯入阻力的影响, 这里结合南海某井场工程实际进行井口导管贯入阻力退化分析。井场导管直径=0.762 m, 贯入深度80 m。黏土的土体强度剖面为u=0.5+0.87d(kPa),d为土体深度, 黏土的有效容重γ′=6.5 kN/m3。
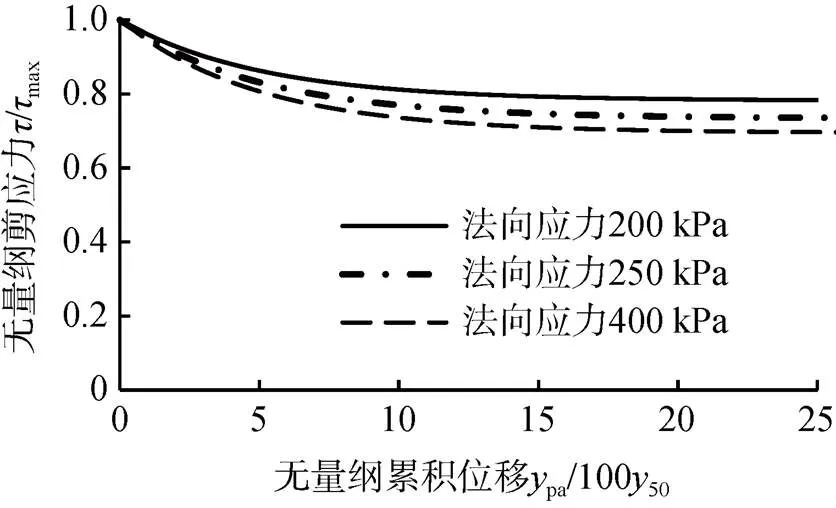
图5 界面剪应力随无量纲剪切位移的退化曲线
喷射导管下入过程中, 喷射水射流对管周土体产生射流砰击力切割土体, 在土体中产生超孔隙水压力对土体产生扰动, 导致管周土体强度降低。其产生超孔隙水压力由以往研究[24]可知约为6.02ui。由式(6)v′=v–6.02ui可以得到喷射扰动后的界面阻力。
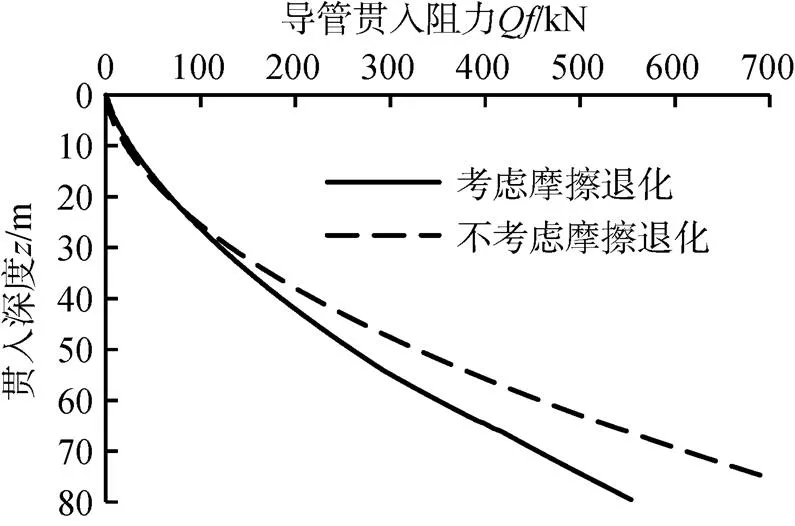
图6 摩擦退化对导管贯入阻力的影响
图6中给出了考虑摩擦退化与不考虑退化导管贯入阻力随着深度的变化曲线。从图中可以看出, 由于土体强度随深度线性增大导管贯入阻力随着贯入深度都是呈现非线性增加。管土界面摩擦退化效应在贯入初期对贯入阻力的影响并不显著, 但随深度增大, 土体强度增大其影响逐渐明显。80 m深度处, 考虑摩擦退化和不考虑摩擦退化得到的贯入阻力分别是455.3 kN、611.4 kN, 考虑摩擦退化后贯入阻力下降28.5%。
5 结论
本文针对深水井口导管大位移贯入界面摩擦退化现象, 采用GDS界面剪切仪进行管土大位移单调剪切试验研究, 揭示大位移剪切界面摩擦力的退化机理, 提出了界面剪应力退化的计算方法, 得到的结论如下:
(1)单调大位移剪切时, 由于黏土颗粒的重新定向排列, 界面剪应力出现应力退化。且剪切土样产生了剪缩现象, 大部分发生在0~10 mm剪切位移范围内, 占总剪缩量的90.1%。
(2)基于界面剪切试验残余强度与初始强度比值, 拟合得到土体的黏聚力系数和灵敏度系数。
(3) 基于剪应力随无量纲剪切位移的退化规律, 提出了钢-黏土界面剪应力随无量纲位移的退化计算方法。
(4)南海某井场工程实际算例的计算结果表明, 考虑界面阻力退化的导管总贯入阻力减小28.48%。
[1] 杨进, 傅超, 刘书杰, 等. 超深水浅层建井关键技术创新与实践[J]. 石油学报, 2022, 43(10): 1500-1508. YANG Jin, FU Chao, LIU Shujie, et al. Key technological innova-tion and practice of well construction in ultra-deepwater shallowformations[J]. Acta Petrolei Sinica, 2022, 43(10): 1500-1508.
[2] 王腾, 孙宝江. 深水喷射井口结构套管水平承载力[J]. 中国石油大学学报(自然科学版), 2008, 32(5): 50-53. WANG Teng, SUN Baojiang. Lateral bearing capacity of jetting structural casing of wellhead in deepwater[J]. Journal of China University of Petroleum (Edition of Natural Science), 2008, 32(5): 50-53.
[3] 唐海雄, 罗俊丰, 叶吉华, 等. 南海超深水喷射钻井导管入泥深度设计方法[J]. 石油天然气学报, 2011, 33(3): 147-151. TANG Haixiong, LUO Junfeng, YE Jihua, et al. Method of design of conductor setting depth for ultra-deepwater jetting drilling in South China Sea[J]. Journal of Oil and Gas Technology, 2011, 33(3): 147-151.
[4] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[S]. Washington D C, US: American Petroleum Institute Publishing Services, 2005.
[5] DOHERTY P, GAVIN K. Shaft capacity of open-ended piles in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1090-1102.
[6] MUHAMMED R D, CANOU J, DUPLA J C, et al. Evaluation of local soil-pile friction in saturated clays under cyclic loading[J]. Soils and Foundations, 2018, 58(6): 1299-1312.
[7] DOHERTY P, GAVIN K. The shaft capacity of displacement piles in clay: a state of the art review[J]. Geotechnical and Geological Engineering, 2011, 29(4): 389-410.
[8] RANDOLPH M F. Science and empiricism in pile foundation design[J]. Geotechnique, 2003, 53(10): 847-875.
[9] CHAKRABORTY D, KUMAR J. Bearing capacity of piles in soft clay underlaid by cohesive frictional soil[J]. International Journal of Geomechanics, 2013, 13(3): 311-317.
[10] ZHOU H, RANDOLPH M F. Resistance of full-flow penetrometers in rate-dependent and strain-softening clay[J]. Geotechnique, 2009, 59(2): 79-86.
[11] KIM Y H, HOSSAIN M S. Numerical study on pull-out capacity of torpedo anchors in clay[J]. Geotechnique Letters, 2016, 6(4): 1-8.
[12] AKERS T J. Jetting of structural casing in deepwater environments: job design and operational practices[J]. SPE Drilling & Completion, 2008, 23(1): 29-40.
[13] CHEN W, ZHOU H, RANDOLPH M F. Effect of installation method on external shaft friction of caissons in soft clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 605-615.
[14] 郭聚坤, 寇海磊, 许泓霖, 等. 桩-海洋黏土界面剪切性状试验研究[J].长江科学院院报, 2019, 36(4): 104-108, 117. GUO Jukun, KOU Hailei, XU Honglin, et al. Study on interface shear behavior between pile and marine clay[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(4): 104-108, 117.
[15] 王永洪, 张明义, 白晓宇, 等. 不同含水率状态下黏土-混凝土界面剪切特性室内试验研究[J].防灾减灾工程学报, 2018, 38(1): 118-123. WANG Yonghong, ZHANG Mingyi, BAI Xiaoyu, et al. Laboratory experimental study on shear behavior of clayey soil-concrete interface under different moisture conditions[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(1): 118-123.
[16] 闫澍旺, 林澍, 贾沼霖, 等. 海洋土与钢桩界面剪切强度的大型直剪试验研究[J]. 岩土工程学报, 2018, 40(3): 495-501. YAN Shuwang, LIN Shu, JIA Zhaolin. Large-scale direct shear tests on shear strength of interface between marine soil and steel piles[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(3): 495-501.
[17] 王永洪, 张明义, 白晓宇, 等. 剪切速率对黏性土混凝土界面抗剪强度影响的试验研究[J]. 土木与环境工程学报(中英文), 2019, 41(1): 48-54. WANG Yonghong, ZHANG Mingyi, BAI Xiaoyu, et al. Experimental research on effect of shear rate on shear strength of clayey soil-concrete interface[J]. Journal of Civil and Environmental Engineering, 2019, 41(1): 48-54.
[18] 赵刚, 李驰, 斯日古楞. 温度循环下桩土界面特性及桩侧摩阻力数值模拟[J]. 防灾减灾工程学报, 2017, 37(4): 546-550, 564. ZHAO Gang, LI Chi, SI Riguleng. Friction characteristics of pile soil interface under temperature cycles and numerical simulation of shaft resistance[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(4): 546-550, 564.
[19] TSUBAKIHARA Y, KISHIDA H, NISHIYAMA T. Friction between cohesive soils and steel[J]. Soils and Foundations, 1993, 33(2): 145-156.
[20] 孔令伟, 熊春发, 郭爱国, 等. 海积软黏土的强度特性与桩土界面剪切速率效应[J]. 岩土工程学报, 2017, 39(S2): 13-16. KONG Lingwei, XIONG Chunfa, GUO Aiguo. Effects of shear rate on strength properties and pile-soil interface of marine soft clay[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 13-16.
[21] TAHA A, FALL M. Shear behavior of sensitive marine clay-steel interfaces[J]. Acta Geotechnica, 2014, 9(6): 969-980.
[22] EINAV I, RANDOLPH M F. Combining upper bound and strain path methods for evaluating penetration resistance[J]. International Journal for Numerical Methods in Engineering, 2005, 63(14): 1991-2016.
[23] WANG T, LIU W. Development of cyclic p-y curves for laterally loaded pile based on T-bar penetration tests in clay[J]. Canadian Geotechnical Journal, 2016, 53(10): 1731-1741.
[24] WANG T, SONG B. Study on deepwater conductor jet excavation mechanism in cohesive soil[J]. Applied Ocean Research, 2019, 82: 225-235.
Experimental study on soil-conductor interface friction degradation of wellhead in deepwater
LIU Shu-jie1, HE Lian1, LIU Zheng1, BAO Xing-xian2, WANG Teng2
(1. CNOOC Ltd. Hainan, Haikou 570312, China; 2. School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China)
The penetration resistance of a deep-water conductor in clay is closely related to its friction resistance at the conductor–soil interface. During the installation of this conductor, considerable displacement occurs at the soil–pipe interface, causing degradation in the friction at the conductor–clay interface. Conventional shear testing devices cannot accurately describe this degradation mechanism at the conductor–soil interface under large displacement shear during the conductor penetration; therefore, in this study, to address this limitation, the GDS multifunctional interface shear testing apparatus was used to conduct large displacement monotonic shear tests under constant stress conditions. The aim was to investigate the influence of normal stress on the degradation mechanism of friction at the conductor–soil interface. The experimental results indicate that during the monotonic shear, the interfacial shear stress initially increases with shear displacement and then decreases, eventually reaching a stable state. The interface exhibits shear stress degradation. With increasing normal stress, the peak stress and residual stress at the interface also increase. The normal displacement of the soil sample increases with shear displacement and normal stress and eventually reaches a stable value. Based on the analysis of the experimental data, a simple method is proposed to calculate the interfacial shear stress with increasing dimensionless displacement considering the shear stress degradation mechanism. Finally, by combining an engineering case study of a conductor at a depth of 80 m, degradation of the interfacial friction is demonstrated to have reduced penetration resistance by 28.48%.
conductor; penetration resistance; adhesive contact interface; friction degradation; interface shear test
Dec. 14, 2022
[National Natural Science Foundation of China, No. 52078483]
P75
A
1000-3096(2023)10-0025-07
10.11759/hykx20230904004
2022-12-14;
2023-09-04
国家自然科学基金项目(52078483)
王腾(1973—), 男, 山东海阳人, 博士, 教授, 主要从事海洋岩土工程方面研究, E-mail: wteng73@upc.edu.cn
(本文编辑: 丛培秀)

