基于大数据的电池特征参数提取和SOC估算方法①

卢宇轩,李 晟,林仕立,张先勇

(1.广东技术师范大学,广东 广州 510665;2.水发兴业能源(珠海)有限公司,广东 珠海 519085)

0 引言

风能和太阳能是重要的新能源发电类型,但均具有波动大、难预测等特点。为了使新能源发电能够跟踪发电计划,业内普遍认为需要配套一定规模的电池储能电站进行调节。然而,随着近年来大量储能电站的出现,一些技术缺陷也开始集中暴发。考虑复杂环境的影响,为了准确追踪电池容量特性并建立模型,以提高储能系统在目标状态下的精准控制[1-2],开发一套行之有效的电池储能电站运维系统势在必行。

运维工具的主要作用在于提高电池储能电站中大量电池单体的一致性,而实现电池荷电状态(state of charge,SOC)的精确估算是其中最关键的基础问题。传统上,电池SOC通过对电池单体或电池组进行多次充放电实验,建立模型并利用算法进行求解。利用多种算法结合的方式可对求取多目标模型有更好效果[3-4]。林春景等人[5]基于实验验证了环境温度对电池内阻的影响,在一定状态下,随着温度降低,充放电欧姆内阻和极化内阻均增加,而对温度更为敏感的欧姆内阻增加幅度更大。另外电池内阻的变化会导致电池可用容量和功率特性的衰减,因此要提高电池可用容量及SOC估算精度,应该着重考虑电池工作温度[6]。此外,电池的充放电倍率对可用容量的影响也极为关键。在相同温度下,较大的放电倍率会导致电池可用容量急剧下降[7],陈育哲[8]的实验结果表明,2 C放电倍率相比1/2 C工况,可用容量衰减超出20%。受电池内阻等诸多因素的影响,电池在不同剩余容量状态下的充放电效率并不相同,低SOC区间与高SOC区间的实际放电或充电容量差异较大。当该区间能量能够充分释放时,总可用容量更多,SOC斜率更平缓,反之更陡峭[9-10]。

由上述内容可知,电池SOC的估算受到多个参数的耦合影响。为了改进传统的SOC估算方法,针对不同工况进行容量调整[11-12],结合多个因素对SOC的影响,提出了实时的电池容量修正因子,以减小估算误差[13]。此外,结合多种估算方法也可提高SOC的估算精度[14]。基于建模的方法,通过实时追踪不同工况下各表征参数与电池可用容量及SOC的对应关系,可以实现电池SOC的精确估算。然而,对于电池储能电站运维工具而言,其使用场景一般不具备开展电池多次充放电实验的条件,且所面向的电池型号也不相同。因此,电池SOC建模方法难以在运维工具上有效应用。考虑到电池储能电站与其监控系统之间存在海量的数据交互,本文提出基于大数据的电池特征参数提取方法,以实现电池SOC估算方法中参数的辨识和调整,从而为电池储能电站运维工具提供高精度的电池状态参数。

1 SOC估算及参数获取方法

电池SOC是电池管理系统中的一个重要参数。一方面是电池储能电站实现充放电控制的主要参考因素,另一方面也是衡量电池组一致性的重要指标。其一般定义如式(1)所示[15]。

(1)

1.1 传统SOC估算方法

基于式(1)的定义,多数实际工程采用“开路电压法+安时积分法”实现电池单体SOC的实时估算,其估算方法如式(2)所示[16]。

(2)

式中:SOC0为初始时刻或者上一时刻的SOC值,I为当前积分时间段的电流,Qa为当前积分时间段电池的实际可用容量。采用开路电压法对SOC0进行估算,并采用安时积分法对电池充放电过程进行计算,可以得到当前的电池SOC值。

从式(2)可知,电流I和积分时间的测量较为精确,因此在电池单体SOC估算过程中,SOC0和Qa的准确计算是影响SOC精度的关键所在,两者与电池的充放电特性息息相关。一方面,传统上一般通过大量实验,包括不同充放电倍率、不同环境温度等条件下的测试,来获得电池的相关特性,进而得到电池SOC0、Qa与端电压、充放电倍率、温度、SOC所处区间等参数之间的关系。另一方面,电池组SOC与各单体SOC之间存在一定的关系,但其影响关系较难获得。因此,在实际应用中,多数采用“平均模型”,通过电池单体的特性来等效衡量电池组的特性,从而得到电池组SOC的估算方法。

1.2 特征参数获取方法

在电池健康状态较好、运行工况稳定的情况下,基于“开路电压法+安时积分法”的SOC估算方法在精度上可以满足电池储能电站运维工具的需求,且具有使用便捷、硬件要求低等优势,是一种较好的估算方法。然而,该方法在实际应用中需要解决如何获取算法中所需电池特性参数的问题。

考虑到电池储能电站电池管理系统(battery management system,BMS)与后台能源管理系统(energy management system,EMS)之间存在海量的数据传输,其中包含了电池簇SOC、电池簇的平均电压、电池簇的充放电电流、簇平均温度、当前状态所持续的时长等相关信息。因此,可以从BMS历史数据提取上述信息,通过数据分析获得电池SOC与相关参数的对应关系,从而实现电池SOC实际值的估算。

具体而言,相关参数用于实现“开路电压法+安时积分法”中SOC0、Qa的辨识,其影响因素主要包括电压、温度、充放电状态、充放电电流、静置时间等。由此可以得到,SOC估算方法的整体逻辑过程如图1所示。

图1 SOC估算方法的逻辑过程

2 基于大数据的SOC0和Qa修正方法

如上节所述,电池SOC估算精度取决于初始状态SOC0以及不同状态下电池实际容量Qa的实时调整。在实际运行过程中,电池的各项参数和工作环境一直处于非线性的变化状态,因此可以基于历史采样大数据,把特性相近的电池运行状态信息进行分类、筛选、组合,并作归一化处理,最后将SOC0及Qa动态修正模型导入“开路电压法+安时积分法”的估算式中。

2.1 SOC0估算方法

影响SOC0的主要参数是电池端压和电池充放电电流。模型的设计思路是把采集的数据按照电流划分为多个电流区间,对每个电流区间选取一定数量的目标值。根据历史大数据,可以通过电流数值将电池分为充电状态、放电状态和静置状态。进一步根据时间参数获取时长,将静置状态细分为长时间静置状态、充电截止恢复状态、放电截止恢复状态。在区分历史数据中电池采样数据所属状态的前提下,可以得到电池SOC0的特征数据提取和分析步骤,具体流程如图2所示。

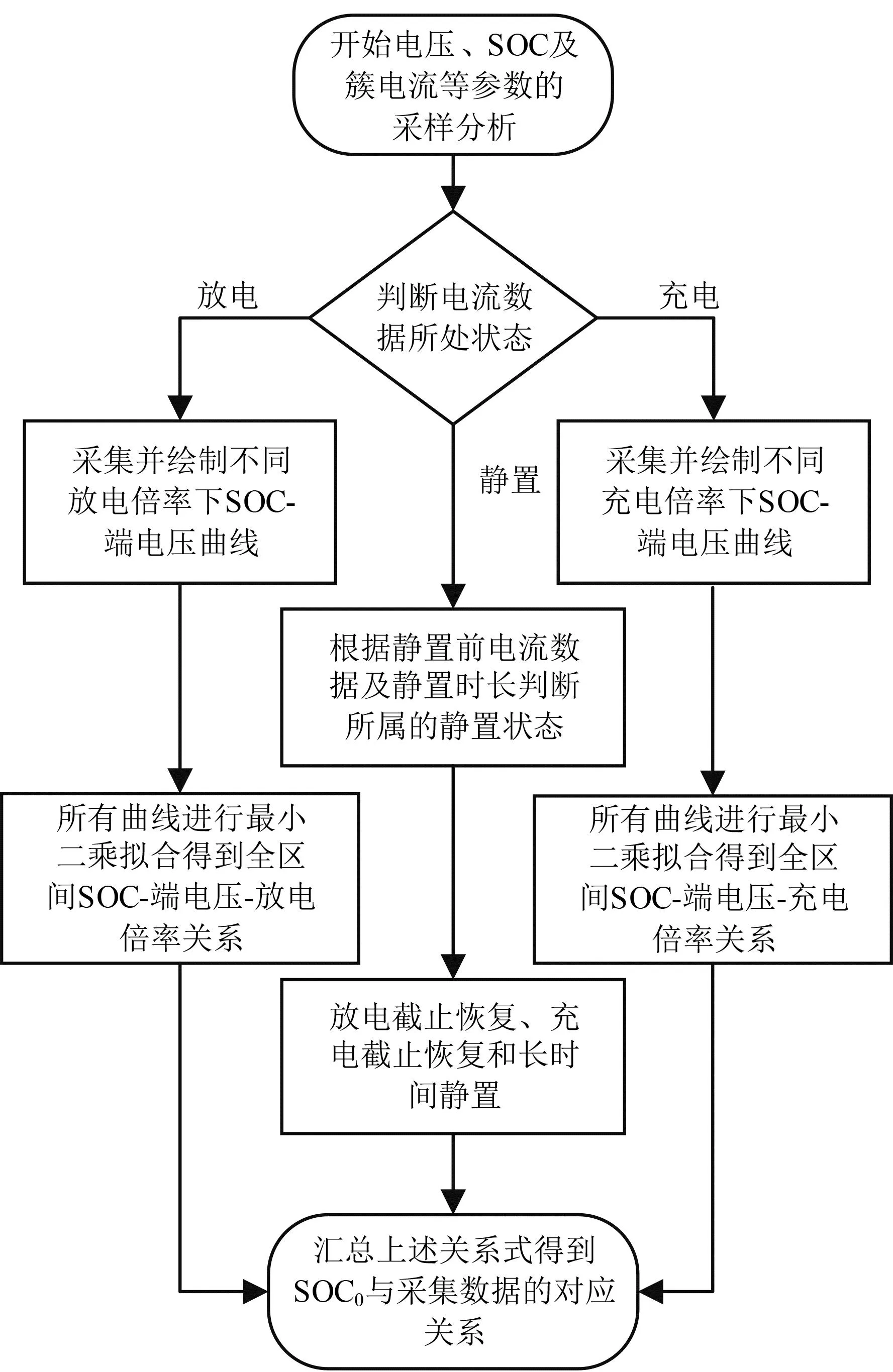
图2 电池SOC0的特征数据提取和分析

2.2 Qa动态调整模型

对于安时积分法中的Qa,其主要受到电池充放电电流和SOC的影响。因此,首先把SOC划分为若干个区段,结合电池的历史数据,通过计算采集时间内Δt的变化及对应的ΔSOC比值,估算该区间内能释放或充入的电能容量和可用总容量的对应关系。因此,Qa可由式(3)得到。

(3)

式中:Qa为电池可用总容量;ΔQ为采集时间内的变化容量;ΔSOC为采集时间内变化SOC。

其中,ΔQ可通过式(4)计算得到,为简化其计算,一般可取本采样时段电流均值的时间乘积进行求取。ΔSOC则可通过式(5)计算得到。

(4)

(5)

式中:T为采集周期/n,即为每个电流变化时段内时长;i0,…,in为采集时间内多次变化电流值;SOCt1和SOCt0分别为本时刻和上一时刻的SOC值。

根据式(3)～式(5),通过对采集时段的电流积分可以得到充放电容量,再结合历史数据中的SOC变化情况,可得到本SOC段对应的Qa值。具体可以把SOC平均划分为五个区段,[0%,20%)、[20%,42%)、[42%,62%)、[62%,82%)、[82%,100%],每个区间段均选取多个充放电倍率下的数据,其中电流和监测SOC采样时间可按照分钟进行设计。

2.3 基于最小二乘法的参数拟合

经过预处理和归一化的整合SOC0和Qa特性数据可作为驱动电池状态估算的完整特性。而最小二乘法是最常用的参数拟合方法,它可以得到较小的目标函数误差。最小二乘法的目的是使拟合的目标函数尽可能地减少与观测值之间的误差,这在公式上体现为使预测值与目标值之差的平方和最小化。因此,对于多组监测到的电池数据,可以通过在各组采集数据之间插入目标函数,并使用最小二乘法进行拟合,来覆盖应用的整个数据范围。基于最小二乘法的参数拟合如式(6)～式(8)所示:

Y=B0+B1x+B2x2+B3x3+…+Bpxp

(6)

(7)

使得

(8)

根据上述对SOC0和Qa进行预处理后的数据特性以及基于最小二乘法的参数拟合方法,可以通过比较多组模型来找到最适合的拟合模型。

3 实验及分析

本实验数据来源于水发兴业能源(珠海)有限公司在西藏地区运行的融合一号舱电池储能电站。所使用的数据来自磷酸铁锂电池串联而成的电池簇,其额定容量为25 Ah。采集监测的是电池簇电流、SOC、Qa,而电压为电池簇的平均电压。由于电池在恒温环境中运行,因此温度的影响不考虑。

3.1 SOC0估算结果及分析

结合融合电池舱历史数据,可以得到电池充电电压、放电电压与SOC的特性曲线,如图3所示。在储能电站运行期间,根据需求,串联电池组以不同的充放电倍率运行,筛选出各倍率数据组电流倍率相互分散并稳定运行相当长时间的数据点作为特征曲线的参考数据。充电曲线共采样了0 A(0 C)、16.16 A(0.65 C)、36.83 A(1.47 C)、44.19 A(1.77 C)、45.66 A(1.83 C)5个电流数据点的数据;放电曲线共采样了13.4 A(0.54 C)、43.79 A(1.75 C)、45.47 A(1.82 C)、50.61 A(2 C)4个电流数据点的数据。

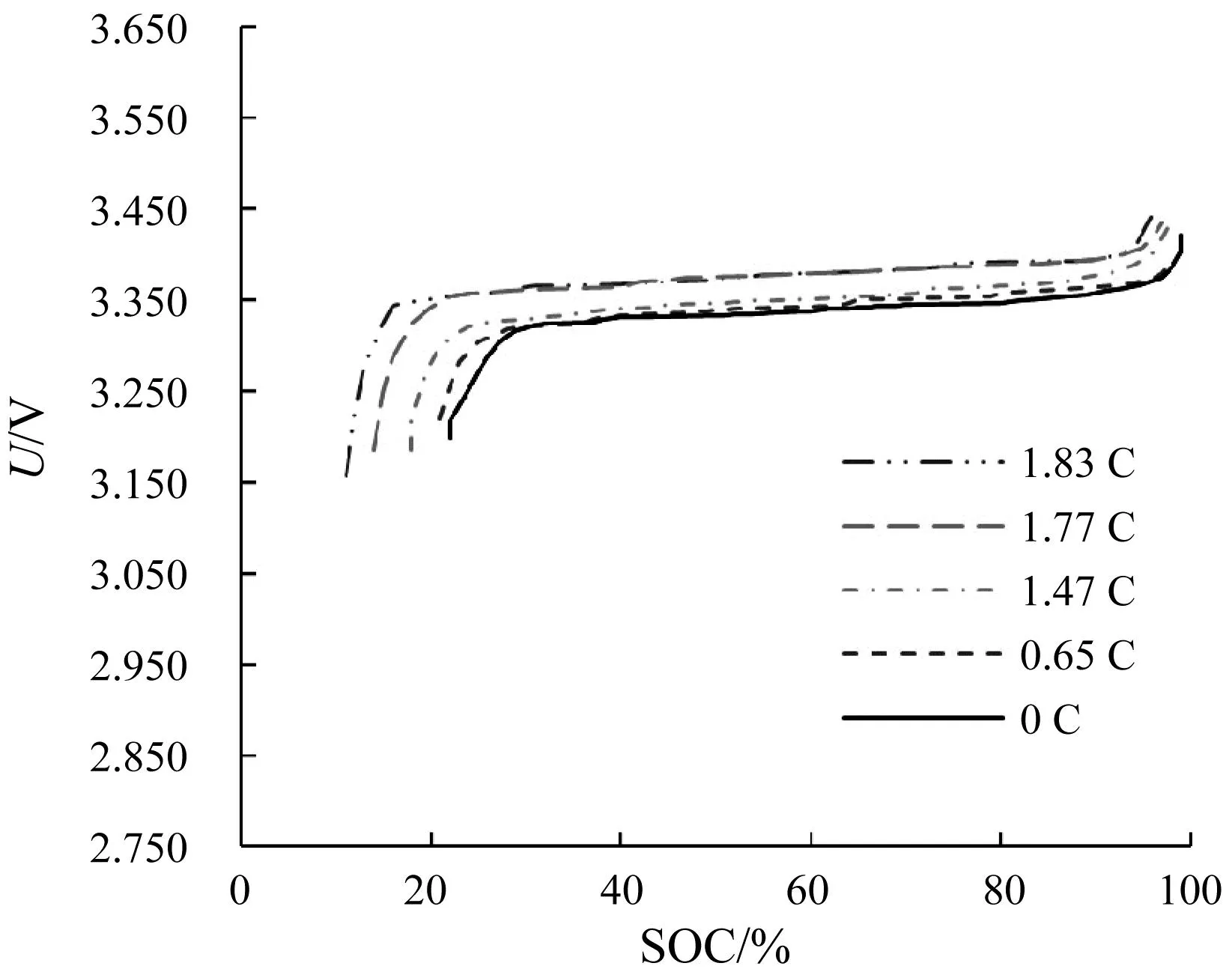
(a)充电工况

从图3的充电工况曲线数据可以看出,在电压平台期,SOC从25%上升至90%,涵盖了大部分的充电过程,而电压的变化范围则是3.25～3.325 V。若以恒定U-SOC曲线作为SOC0的电压参考,会造成35%～55%的ΔSOC。通过SOC0的优化模型,可大大改善初始SOC估算偏移较大的问题,提高估算算法的可靠性。

在电压和电流的共同影响下,对SOC0数据进行模型拟合能更好地反映观测值的函数特性。因此,根据最小二乘法找到拟合模型的最适参数点作为SOC的模型函数,选用扩展S形模型对采样点进行数据拟合,可以得到电流-电压-SOC的关系函数模型,模型如图4所示。从图中可以看出,在充电工况下,大倍率充电电池的SOC特性曲线更为陡峭。当充电倍率大于1.2 C时,随着电压的增大,SOC值快速增加。曲线的起始上升点电压随充电倍率的增大而逐渐增大。对于放电工况,电压随着SOC的减小而逐渐降低,但在0.4 C时,随着SOC的减少,电池端电压有较陡峭的下降,而高倍率放电则下降较为平缓。相同SOC容量下,电池端电压会随着放电倍率的增大而逐渐降低。而高倍率工况所能释放的SOC比小倍率的要少。

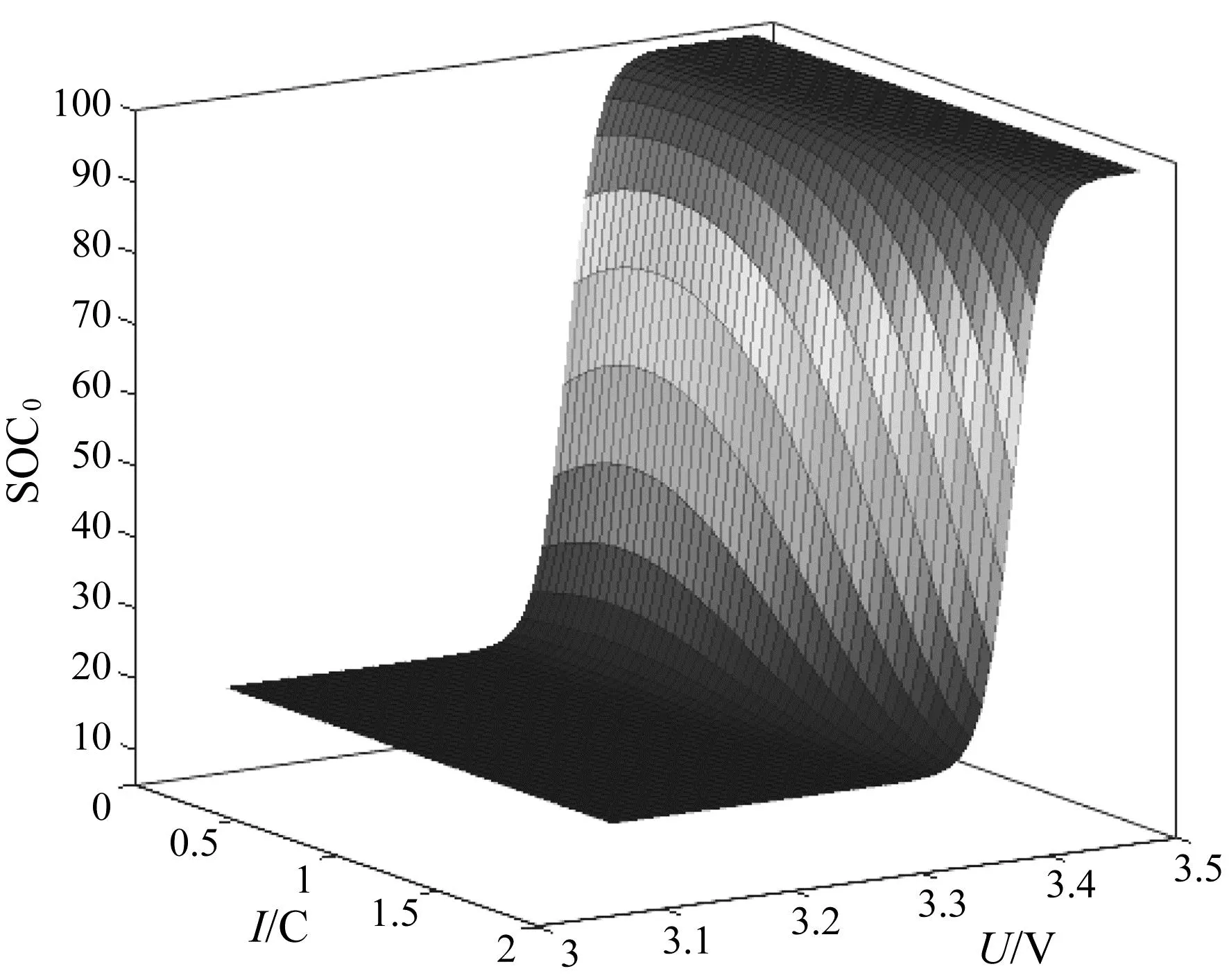
(a)充电工况

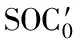
(9)

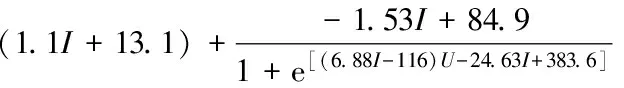
(10)

3.2 Qa影响关系分析

电池可用容量Qa的实时修正受到SOC和电流的影响。通过对电池簇的研究得到如下的分析结果。Qa与SOC的关系曲线如图5所示,从图中可以看到,电池簇充电时,在SOC处于0%～20%及85%～100%时电池可用容量Qa有着明显变化,在充电的起始和结束阶段衰减明显。SOC为20%～85%时,可用容量整体处于相对平稳的状态,随着SOC的增加而略有增加,放电曲线与充电曲线有着相似特性,随着SOC的增加而增大。SOC超过80%之后,Qa实时修正分别受到SOC和电流的影响,呈现下降趋势。SOC在25%～80%区间时,Qa较平稳。

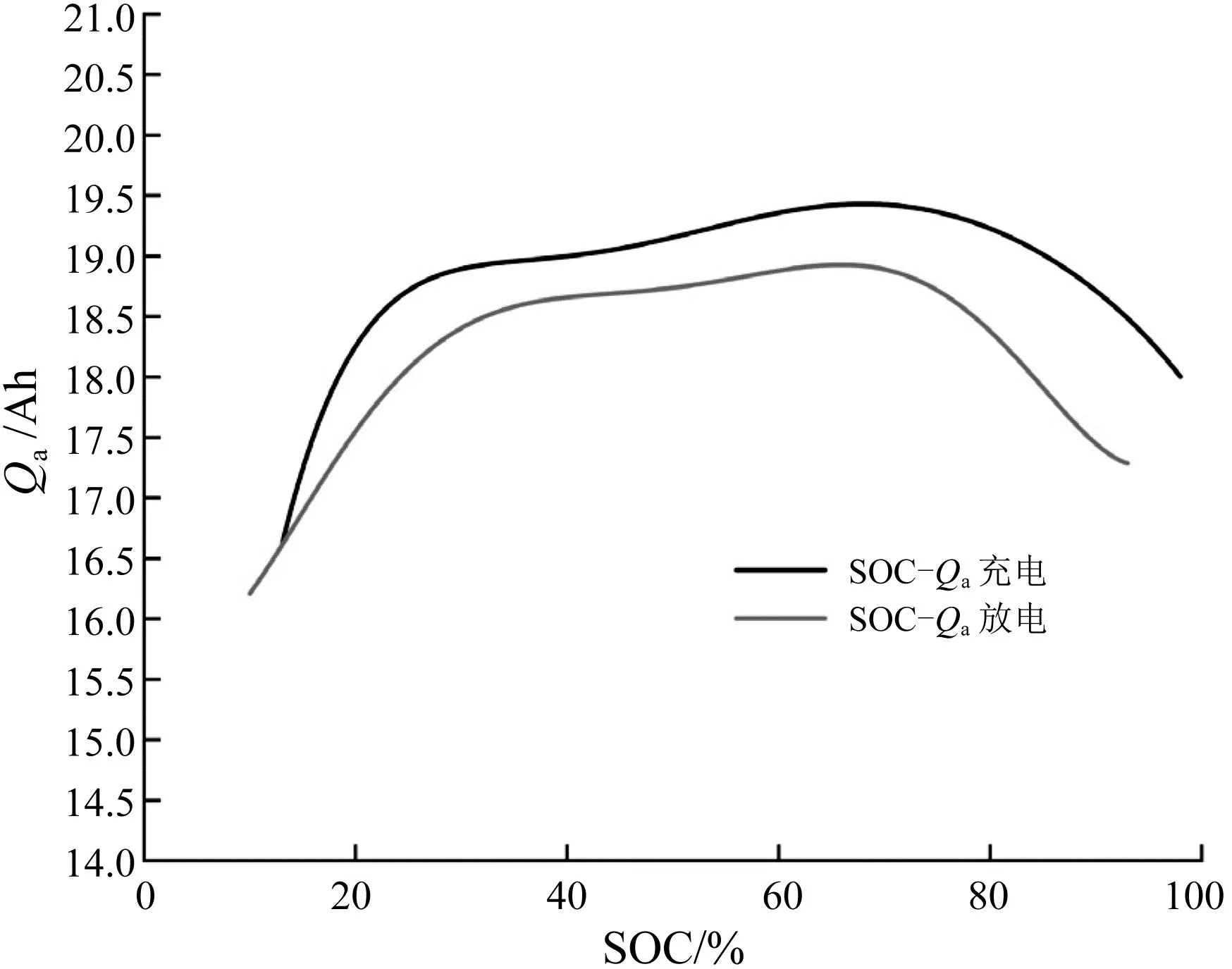
图5 Qa与SOC的关系曲线

通过曲线分析,在整个充放电区间内,Qa最低可下降至16.5 Ah,与额定容量25 Ah相差近34%。若使用Qa进行单位采样时间ΔSOC的估算,最大误差将达到34%。对于充电过程和放电过程,Qa和充放电倍率Crate之间存在一定的特性关系,两者的关系曲线如图6所示。从图6可以看出,随着充电电流的增大,电池的可用总容量Qa基本呈现下降的趋势。在充电倍率小于0.8 C时,Qa相对平缓;充电倍率大于0.8 C时,则出现明显下降;在充电倍率进一步提高到1.8 C时,Qa降到18 Ah。在放电工况下,Qa与充电工况则存在较大差异。在放电倍率小于0.8 C时,Qa有明显下降,0.8～1.8 C内呈现较平缓的趋势,甚至稍有增加。除了在小于0.4 C的情况下,电池容量能达到20 Ah的较高电量,大部分情况下电池簇能放出19 Ah的电量。然而,在大于2 C的大电流放电状态下,可放出的电量会快速减少。

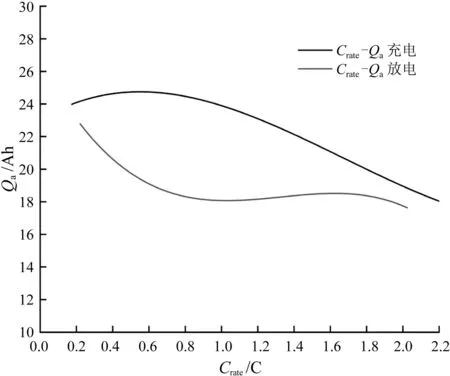
图6 Qa与充放电倍率的关系曲线

综合考虑充放电倍率对Qa的影响,超过1.8 C倍率的工况使得可用容量下降到18 Ah。相较于使用25 Ah额定容量作为Qa,通过模型修正后的ΔSOC单位采样时间下的误差最大会减少28%的估算误差。

(11)

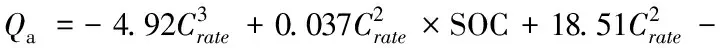
(12)

4 结论

对于电池储能电站等应用场合,无法将电池重新投入实验环境去更新估算模型,因此,通过将电池历史数据作为数据筛选和数据分析的基础,对估算模型参数进行修正,能实现运维工具等外部设备对电池SOC的准确估算。本研究通过SOC、电压、电流等历史数据,对“开路电压法+安时积分法”中的初始荷电状态SOC0和实际可用容量Qa进行了修正,可以有效提高该算法的估算精度,大大扩展了该方法的适用范围。