多节λ/4阻抗变换器的频率特性与变换比
贺昌辉 张 迪 陈一畅 肖 慧
(空军预警学院,武汉 430019)
微波技术与天线[1]教材关于多节λ/4阻抗变换与变换比之间的关系有这样的描述:
多节λ/4阻抗变换器由多个λ/4阻抗变换器级联而成。以两节为例(如图1所示),设传输线上的工作频率和中心频率分别为f和f0,其对应的波长分别为λ和λ0)。
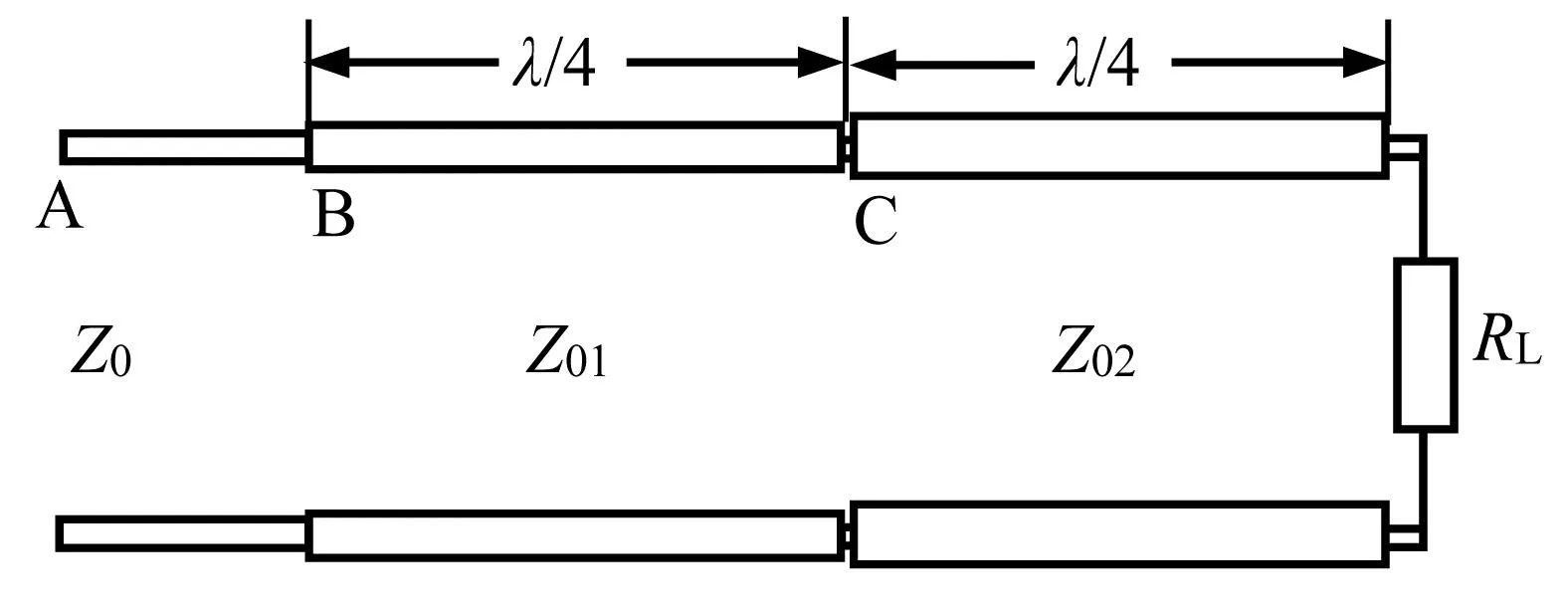
图1 两节λ/4阻抗变换器的组成
当f=f0时,图中C点的输入阻抗
(1)
B点的输入阻抗
(2)
为使主线AB段匹配,须使ZB=Z0,于是,求得特性阻抗比如下:
(3)
记RL/Z02=ξ(变换比),代入上式可得
(4)
多节λ/4阻抗变换器可以改善频率特性,变换比不同,改善的程度也不同。然而,多节λ/4阻抗变换器对频率特性的改善与变换比之间到底满足怎样的关系教材中却没有详细说明,这不免会引起读者的困惑,因此需要通过理论推导和仿真分析对这一结论进行解释。
1 频率特性与变换比的关系推导
多节λ/4阻抗变换器的电长度应为λ0/4,如果f=f0,则主线AB段完全匹配。但是在其他频率电长度是不同的,所以当f≠f0时,主线AB段不再完全匹配,处于失配状态,下面推导失配与频率之间的表达式。
设B点反射系数为
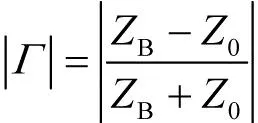
(5)
其中
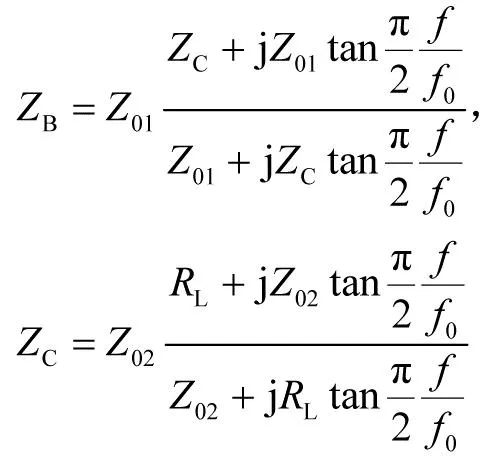
(6)
将式(4)和式(6)代入式(5),可得两节λ/4阻抗变换器的频率特性与变换比之间的关系为
(7)
2 仿真与分析
2.1 变换比不同,两节λ/4阻抗变换器的频率特性
在式(7)中,令RL=2Z0,当变换比ξ分别为1.0、1.2和1.3时,以|Γ|为纵坐标、f/f0为横坐标得到两节λ/4阻抗变换器的频率特性曲线如图2所示。
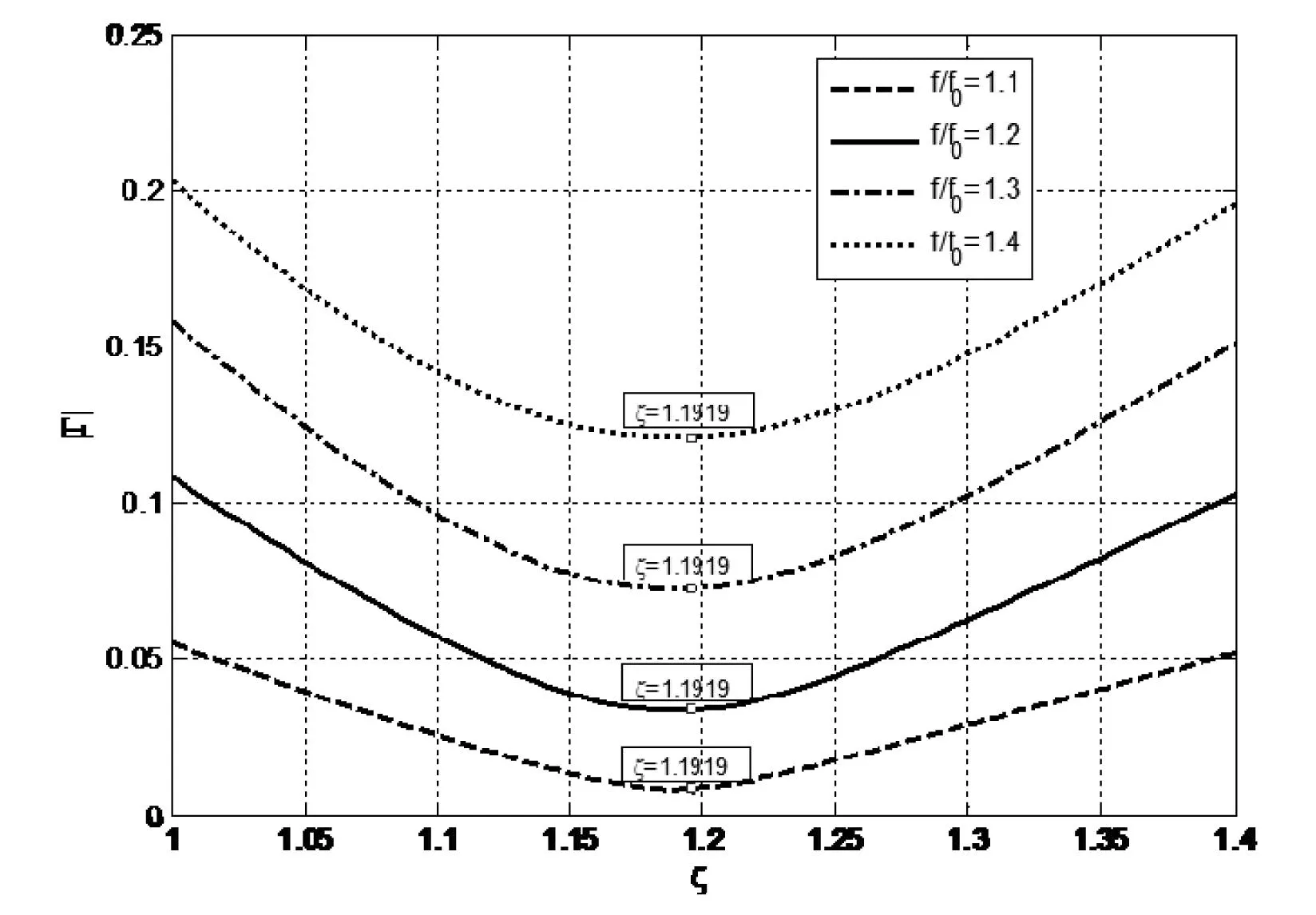
图2 ξ不同时,两节λ/4阻抗变换器的频率特性曲线
由图可见:
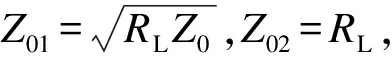
(2)若两节λ/4阻抗变换器最大可容忍的反射系数幅值|Γ|m=0.05[2],则|Γ|≤0.05|Γ|≤0.05所对应的频率范围为两节λ/4阻抗变换器的带宽,带宽越宽,说明阻抗变换器的频率特性越好。很明显图中ξ=1.2和ξ=1.3所对应的带宽明显高于ξ=1.0的带宽,也就是ξ=1.2和ξ=1.3时的带宽获得了有效的展宽,可见两节λ/4阻抗变换器能很好地改善频率特性,且变换比ξ不同,改善的程度也不同。图中ξ=1.2时的带宽最宽,改善频率特性的程度最好。
2.2 负载RL不同,两节λ/4阻抗变换器的频率特性
在式(7)中,令f=1.3f0且RL/Z0分别为2、4和6时,以|Γ|为纵坐标、ξ为横坐标得到两节λ/4阻抗变换器的频率特性随变换比 的变化曲线如图3所示。
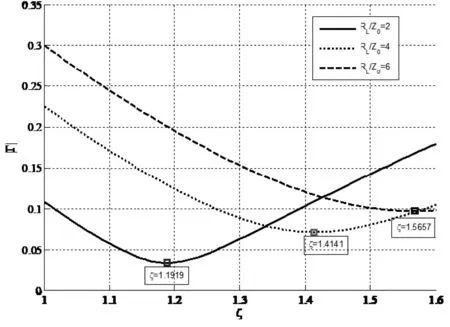
图3 RL不同,|Γ|随ξ的变化曲线
由图可知,每一种负载RL,两节λ/4阻抗变换器均有一曲线变化率最小的位置,在该处 最小,阻抗变换器具有最佳的频率特性,其所对应的变换比 称为最佳变换比。负载RL不同,最佳变换比也不相同,图中三种负载的最佳变换比如表1所示。
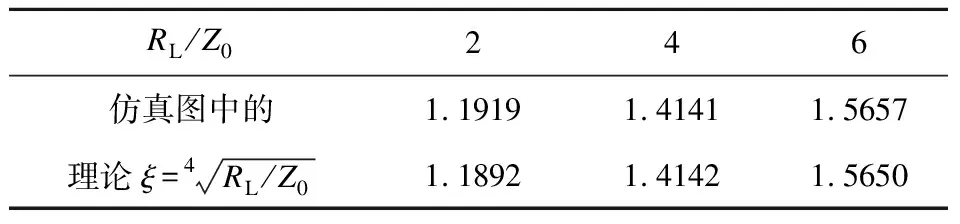
表1 RL/Z0不同时的最佳变换比
从物理概念上讲,两节λ/4阻抗变换器来实现匹配这相当于用分散的不连续性来代替集中的不连续性。当频率变化时,分散的不连续性产生的反射能被抵消掉大部分,从而使频带增宽。因此,两节λ/4阻抗变换器的频带比单节的宽。为了有最佳的频率响应特性,两节λ/4传输线的阻抗变换比通常取一样的[3-4],即
(8)
将式(1)代入式(8),可求得
(9)
将式(2)及ZB=Z0代入式(8),可求得
(10)
由式(9)和式(10)可得
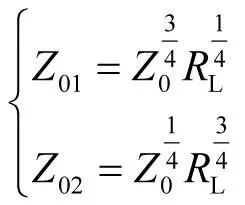
(11)
因此,最佳变换比为:
(12)
当RL=2Z0、4Z0和6Z0时,由式(12)得到的最佳变换比以及仿真图中的最佳变换比如表1所示,可见仿真结果与理论计算的最佳变换比一致。
2.3 f/f0不同,两节λ/4阻抗变换器的频率特性
如图4所示,以|Γ|为纵坐标、以ξ为横坐标,在f/f0=1.1~1.4且RL=2Z0时得到的两节λ/4阻抗变换器的频率特性曲线,可见,当负载不变时,两节λ/4阻抗变换器的最佳变换比不会随工作频率的变化而变化,也就是最佳变换比与频率无关。

图4 f/f0不同,|Γ|随ξ的变化曲线
3 结语
本文以两节λ/4阻抗变换器为例,详细推导了其频率特性与变换比的关系,并对关系式进行仿真分析,验证了两节λ/4阻抗变换器可以很好地改善频率特性,且变换比不同,改善的程度也不同这一重要结论,同时在这些变换比之中,可以找到与频率无关而仅与终端负载有关最佳变换比。按最佳变换比设计的两节λ/4阻抗变换器即可以对纯电阻实现一定频率范围内良好的阻抗匹配,而且结构简单、方便设计,具有较强的实用性。

