基于随机森林回归算法的回采工作面瓦斯涌出量预测

张增辉， 马文伟

（1. 国家能源集团神东煤炭集团有限责任公司 保德煤矿，山西 忻州 036600；2. 中煤科工集团沈阳研究院有限公司，辽宁 抚顺 113122；3. 煤矿安全技术国家重点实验室，辽宁 抚顺 113122；4. 西安交通大学 人居环境与建筑工程学院，陕西 西安 710049）

0 引言

瓦斯灾害是煤矿生产过程中的重大灾害之一，《煤矿安全规程》明确规定，新建矿井或生产矿井新水平都必须进行瓦斯涌出量预测，以确定新矿井、新水平、新采区投产后瓦斯涌出量的大小，将预测结果作为矿井和采区通风设计、瓦斯抽采及瓦斯管理的依据[1-3]。回采工作面是矿井瓦斯涌出的主要场所，精准预测回采工作面的瓦斯涌出量，进而有针对性地提出防治措施，对保证矿井安全生产具有重要意义。

应用最广泛的矿井工作面瓦斯涌出量预测方法包括分源预测法和矿山统计法[1]。分源预测法以煤层瓦斯含量为主要基础数据，结合煤层开采情况进行工作面瓦斯涌出量预测。矿山统计法以瓦斯带内煤层相对瓦斯涌出量与开采深度的关系为基础，利用线性梯度预测延伸水平的瓦斯涌出量。这2 种方法虽然操作性强，现场应用广泛，但在预测过程中考虑的影响因素有限[4]。矿井瓦斯涌出规律和涌出量因地而异，且影响瓦斯涌出量的地质因素较多，各因素之间的非线性关系错综复杂，难以控制。随着信息与计算科学的发展，学者们将灰色理论、神经网络、支持向量机等非线性映射方法用于瓦斯涌出量预测[5-8]。赵建会等[9]运用灰色预测理论，分析了回采工作面瓦斯涌出量的关键影响因素，建立了工作面瓦斯涌出量预测模型。熊祖强等[10]利用无偏灰色模型代替传统灰色模型，建立了动态无偏灰色马尔科夫模型，消除了传统灰色模型自身固有的偏差，提高了预测精度。李树刚等[11]构建了因子分析与BP 神经网络相结合的瓦斯涌出量预测模型，采用因子分析法对瓦斯涌出量影响因素进行分析降维，解决了因预测指标过多导致瓦斯涌出量预测精度降低的问题。付华等[12]采用蚁群聚类算法获取最优Elman 神经网络权值和阈值，完成了瓦斯涌出量与影响因素之间的非线性逼近，并提出了基于蚁群聚类（Ant Colony Clustering，ACC）和Elman 神经网络（Elman Neural Network，ENN）算法的绝对瓦斯涌出量预测模型，实现了动态预测目标。

在实际工程应用中，工作面瓦斯涌出量的影响因素众多且复杂，灰色理论往往精度相对较低，支持向量机预测方法对超参数的选取有较高要求，神经网络算法预测精度依赖于样本容量，且训练速度慢，泛化能力相对较差，在进行工作面瓦斯涌出量预测时有一定局限性[13]。随机森林回归算法能处理高纬度的离散型及连续性数据，具有较强的抗噪声能力和准确性，且理论易于理解，计算简单，故也被应用于工作面瓦斯涌出预测中[14-16]。本文在前人研究的基础上，以工作面实测瓦斯涌出量数据为原始样本，通过Bootstrap 抽样方法进行样本选取，以袋外数据（Out-of-Bag，OOB）作为测试集，通过OOB 评估分数oob_score 进行模型参数调优，建立最优化的随机森林回归模型，进行回采工作面的瓦斯涌出量预测，从而提高预测精度及预测效率。

1 瓦斯涌出量预测方法

1.1 随机森林回归算法原理

随机森林回归算法是由多个决策树构成的一种基于引导聚集算法（Bootstrap aggregating，Bagging）的集成算法[17]，能够有效地在大数据集上运行，处理分类和回归问题。

随机森林回归算法原理如图1 所示。首先，利用Bootstrap 抽样方法从原始训练集中抽取k个与原始训练集样本容量一致的样本；其次，针对k个样本，从M个输入特征中随机选择m个作为决策树分支节点的备选特征（M＞m）；然后，根据特征不纯度指标确定最佳节点和最佳分支，分别建立k个决策树回归模型，得到k个回归预测结果；最后，根据k个回归预测结果求得平均值P，作为最终预测结果。

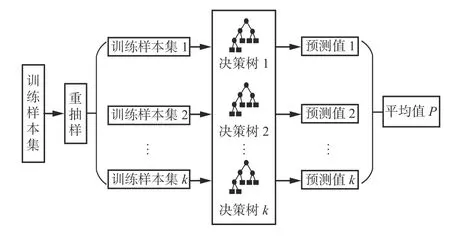
图1 随机森林回归算法原理Fig. 1 Principle of random forest regression algorithm

1.2 模型性能评估方法

Bootstrap 抽样方法通过有放回的随机抽样技术形成不同的训练数据。在一个含有K个样本的原始训练集中进行随机采样，每次采样1 个样本，并在抽取下一个样本之前将该样本放回原始训练集中，共采集K次，最终得到1 个与原始训练集大小相同的由K个样本组成的自助集。由于是随机采样，每次的自助集和原始数据集均不相同，这样即可获得互不相同的自助集。由于是有放回的抽样，某些样本可能在同一自助集中反复出现，而其他有些样本则可能会被忽略。每一个样本被抽到自助集中的概率为当K趋向于无穷大时，概率收敛域为1-1/e，其值约为0.632，即数据集中会有36.8%的训练数据没有参与建模，这一部分数据为OOB。这些OOB 可作为模型的测试集来评估模型性能。评估结果以oob_score 表示，oob_score 返回R2：

式中：u为残差平方和；v为总平方和；N为样本数量；i为样本序号；fi为模型回归值；yi为样本点真实数值标签；yˆ为真实数值标签的平均值。

按照式（1），随机森林中每棵决策树都会产生一个oob_score，将所有决策树的oob_score 进行平均，可得随机森林的oob_score，以此来评估模型性能。

1.3 特征变量重要性评估

数据集中往往特征较多，特征变量重要性评估对模型的降维具有重要作用。用随机森林进行特征重要性评估的思想是判断每个特征在随机森林中每棵树上所作的贡献，而评价贡献大小通常使用基尼指数Gini 或袋外数据错误率oob_error 作为评估指标，本文以oob_error 为例进行说明。

首先，对随机森林中的每一棵决策树，使用相应的OOB 来计算误差，记为 ε1；其次，随机对OOB 所有样本的特征I加入噪声干扰，再次计算OOB 误差，记为 ε2；由于在特征I中加入噪声后，OOB 数据预测准确率会有一定程度下降，假设随机森林中有T棵树，那么特征I的重要性可通过计算得出，其值越大，说明特征I对样本回归结果的影响越大，即重要性越高。

2 数据测试分析

2.1 数据样本

影响工作面瓦斯涌出量的因素众多，根据资料查阅及现场考察，选取14 种特征，包括瓦斯含量X1、煤层埋深X2、开采层厚度X3、煤层倾角X4、回采高度X5、日进尺X6、工作面长度X7、采出率X8、日产量X9、顶板管理方式X10、邻近层瓦斯含量X11、邻近层煤层厚度X12、邻近层与本煤层间距X13、邻近层与本煤层层间岩性X14。测试数据来源于相关文献中山西、江西、安徽等地多个矿井的72 组回采工作面的瓦斯涌出量及相关特征数据[16,18-19]，部分样本数据见表1，其中Y为瓦斯涌出量。为了便于准确对比分析，将每个矿井80%的数据用于模型训练，20%的数据作为模型验证测试对比样本。

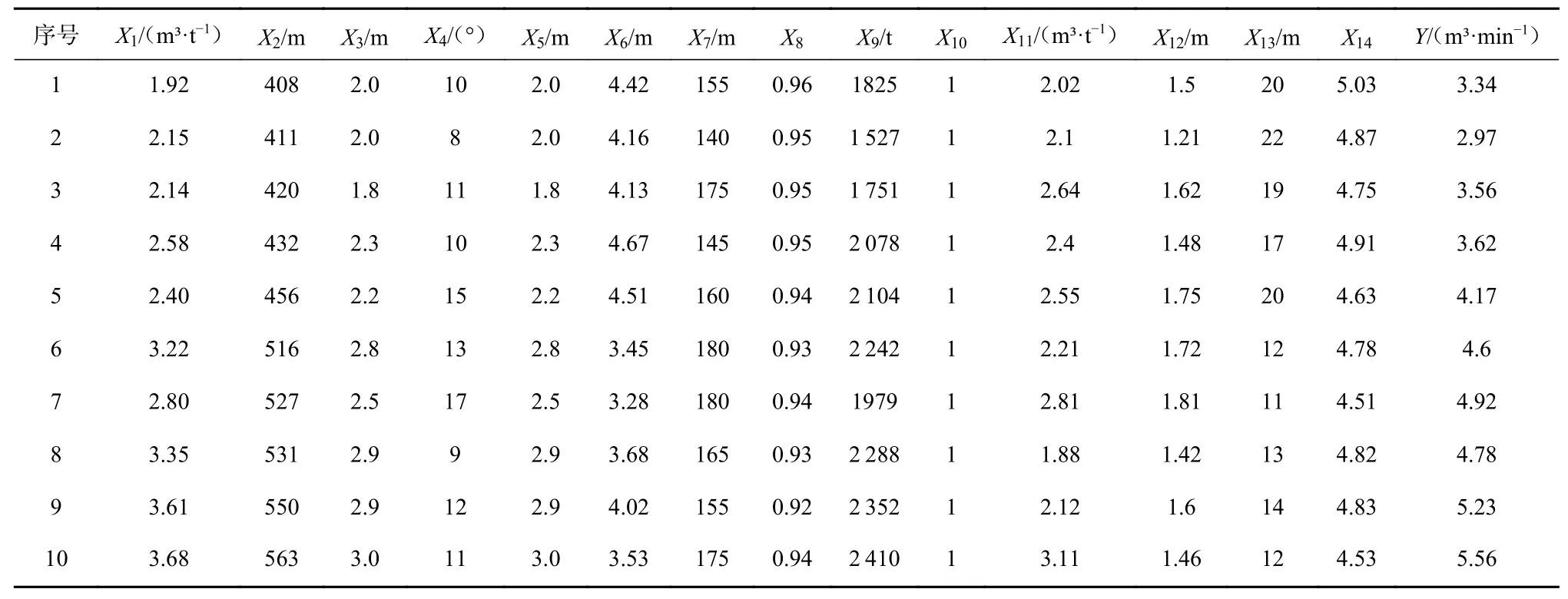
表1 回采工作面瓦斯涌出量特征样本数据Table 1 Sample data of gas emission characteristics in the mining face

2.2 模型构建及参数调整

随机森林回归模型以Python 语言为基础，借助Sklearn 机器学习中的RandomForestRegressor 进行构建。Sklearn 中随机森林回归模型的待调参数共有16 项，其中最主要的待调参数见表2。

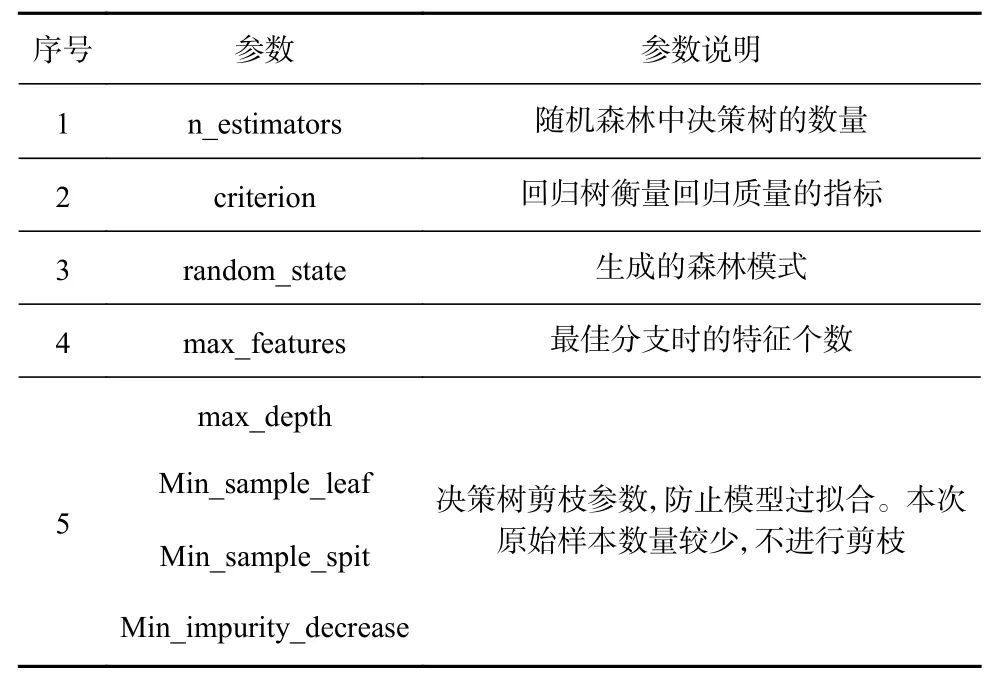
表2 随机森林回归模型主要待调参数Table 2 The main parameters to be adjusted in the random forest regression model

通过试算表明，随机森林回归模型中的n_estimators， criterion， random_state， max_features 都对计算结果有一定的影响。由于回采工作面瓦斯涌出量预测数据样本量较少，所以模型将不进行剪枝，只对n_estimators，criterion，random_state，max_features进行调参。利用Python 语言编制程序， 设置n_estimators 为1～200，criterion 分别为mse，mae 和friedman_mse，random_state 为1～200，max_features为1～14，计算模型的最大obb_score，结果见表3。

表3 随机森林回归模型调参结果Table 3 Parameter adjustment results of random forest regression model

由表3 可看出，当criterion 为mae，n_estimators为20，max_features 为14，random_state 为70 时，根据数据样本所建立的随机森林回归模型obb_score 最大，其值为0.921 164 29。

为了更直观地说明模型所调各参数之间的关系， 绘制criterion 为mae， max_features 为14 时，n_estimators、random_state 与obb_score 的关系热力图，如图2 所示。

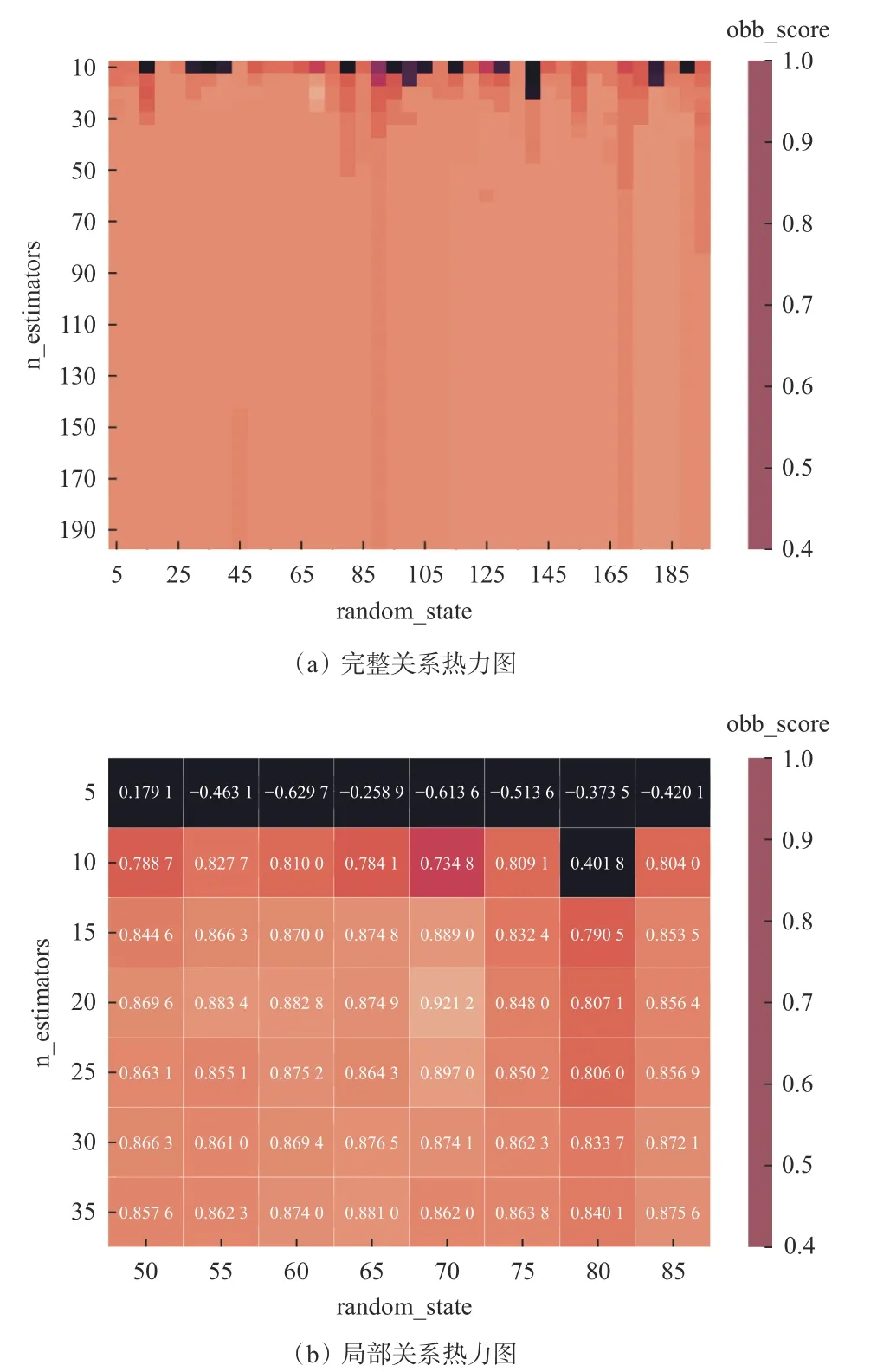
图2 随机森林回归模型参数关系热力图Fig. 2 Thermodynamic diagram of random forest regression model parameter relationship

由图2 可看出，针对工作面瓦斯涌出量数据样本，总体上各种调参组合的obb_score 可达80%以上，只有在n_estimators 较小时，会出现obb_score 较低的情况，但也并非呈现n_estimators 越大，obb_score越高的趋势。从图2（a）中可明显看到，当random_state 不同时，纵向条带分布较为明显，故调整适当的random_state 能够在一定程度上提高模型预测的准确性。

当random_state 为70 时，不同的max_features 所对应的n_estimators 与obb_score 的关系曲线如图3所示。由图3 可看出，针对该数据集，随着n_estimators的增大，obb_score 先急剧增大，后降低至某一水平并逐渐趋于稳定。无论max_feature 为何值，n_estimators在20 左右，obb_score 达到最大值。

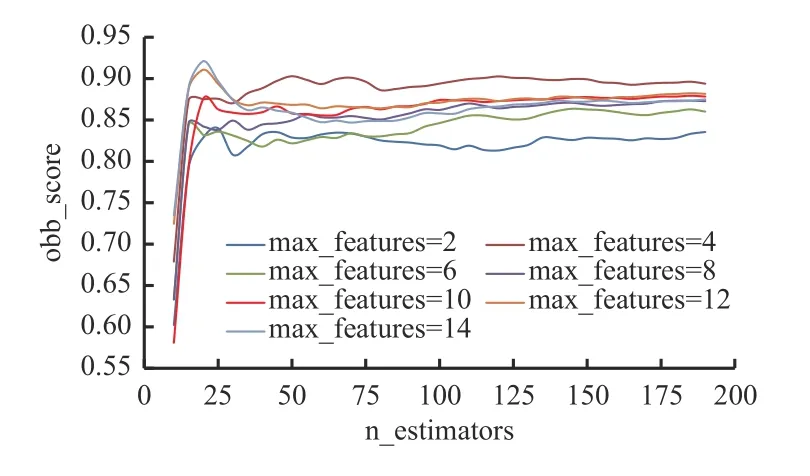
图3 n_estimators 与obb_score 的关系曲线Fig. 3 The relationship curves of n_estimators and obb_score

2.3 特征变量分析

对回采工作面瓦斯涌出量样本数据涉及的14 种特征变量进行重要性评估，重要性占比如图4 所示。按特征重要性排序依次为瓦斯含量X1（33.51%）、煤层埋深X2（21.40%）、日进尺X6（12.97%）、回采高度X5（6.93%）、邻近层与本煤层间距X13（6.57%）、煤层倾角X4（3.21%）、邻近层瓦斯含量X11（2.83%）、开采层厚度X3（2.60%）、邻近层与本煤层层间岩性X14（2.25%）、采出率X8（2.11%）、日产量X9（2.10%）、工作面长度X7（1.87%）、邻近层煤层厚度X12（1.65%）。由于本次数据采集中所有工作面顶板管理方式一致，均设置为1，特征含有效信息，所以顶板管理方式X10的重要性评估为0。

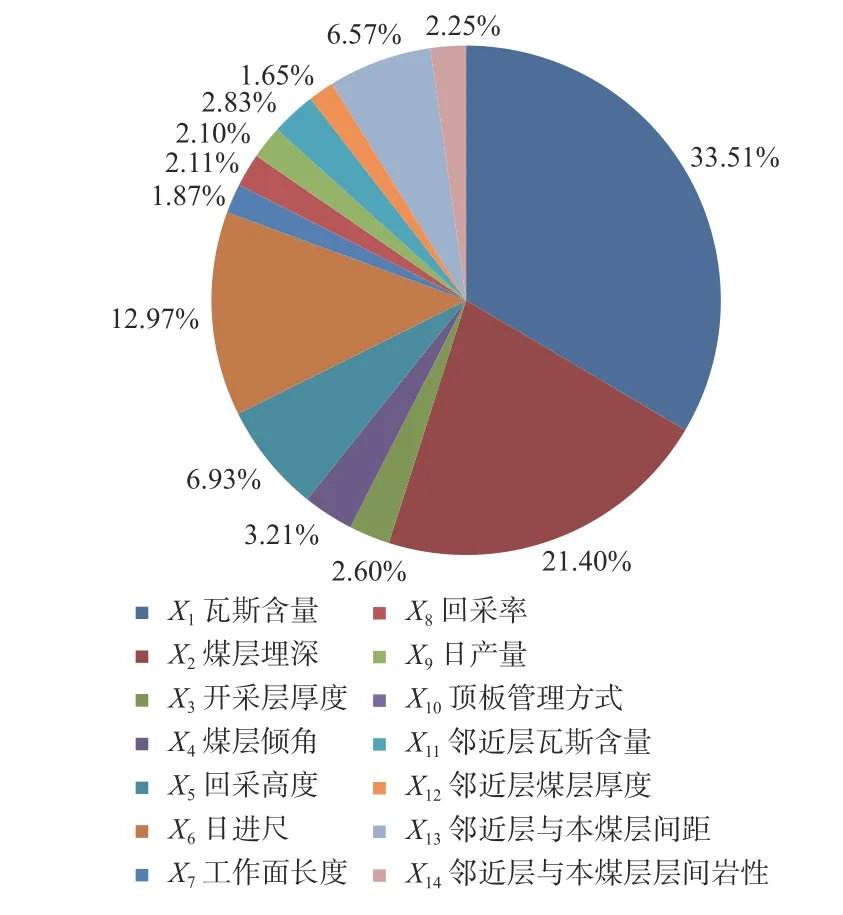
图4 特征变量重要性占比Fig. 4 The proportion of importance of characteristic variables

分析图4 可知，与本煤层相关的特征变量重要性占比总和为86.7%，与邻近层相关的特征变量重要性占比总和为13.3%。可见在依托本数据集建立的随机森林回归模型中，本煤层开采时的数据对于工作面瓦斯涌出量的预测更为重要。

为了分析特征变量的数量对预测模型的影响，按照特征变量重要性排序，分别计算前2～14 个特征变量所构建的13 个随机森林回归模型的最大oob_score，结果如图5 所示。可看出随机森林回归模型的性能随着特征变量数的增加并不会呈现规律性的变化，特征变量数的增加有时降低了模型性能。

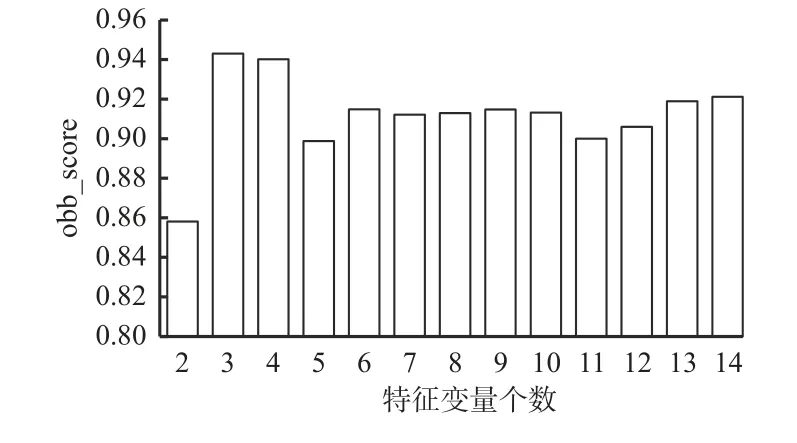
图5 特征变量数与oob_score 关系Fig. 5 The relationship between the number of characteristic variables and oob_score

分析图5 中不同特征变量数对应的obb_score可知，特征变量个数为2 时oob_score 最低，为0.858 15，当特征变量个数为3 或者4 时，oob_score 为0.94 以上，明显高于其余得分，所以当特征变量个数为3 或4 时，可能存在过拟合的情况。

2.4 预测结果分析

按照特征重要性排序，构建特征变量个数为3～14 时的随机森林回归模型，对14 个工作面的瓦斯涌出量预测样本进行预测，预测值与实测值的误差见表4。

分析表4 可知，当特征变量个数为3 或4 时，虽然在训练集中的obb_score 均大于0.94，但在测试集中平均绝对误差和平均相对误差均相对较大，说明当特征变量个数为3 或4 时，存在一定过拟合。当特征变量个数为14 时，平均绝对误差仅为0.005 m³/min，平均相对误差仅为0.77%，预测效果最好。

特征变量数与平均绝对误差、平均相对误差的关系曲线如图6 所示。可看出预测值与实测值的平均绝对误差、平均相对误差随着特征变量数的增加呈下降趋势，增加特征变量数可在一定程度上提高随机森林回归模型的预测效果。

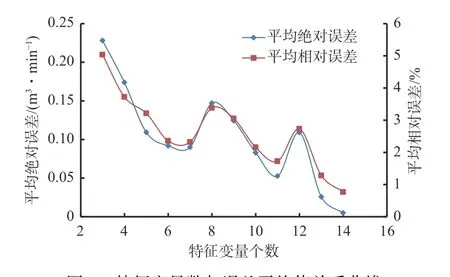
图6 特征变量数与误差平均值关系曲线Fig. 6 The relationship between the number of characteristic variables and mean value of error

将特征变量个数为14 时建立的工作面瓦斯涌出量随机森林回归模型与文献[20]提出的主成分回归分析法进行对比，结果见表5。由表5 可知，随机森林回归模型最小相对误差为1.63%，最大相对误差为5.97%，平均相对误差为4.26%，具有较高的准确性，完全能够满足现场瓦斯涌出量预测需求。与主成分回归分析法相比，随机森林回归模型的平均相对误差降低了14.29%，预测效果更好。此外，相比主成分分析法，随机森林回归模型原理更简单，调参更容易，计算速度更快，能够快速高效地为矿井回采工作面瓦斯涌出量预测提供有力的理论支撑。

表5 不同预测模型预测结果对比Table 5 Comparison of prediction results of different prediction models

3 结论

1） 以矿井实际工作面瓦斯涌出量数据样本为基础，通过随机森林回归模型进行工作面瓦斯涌出量预测。以Bootstrap 抽样方法随机抽取样本，通过oob_score 作为模型调参的标准，得到随机森林回归模型的最优参数。

2） 计算各特征变量的重要性占比并进行排序，按照重要性排序进行随机森林回归模型性能分析，结果表明，随着特征变量数的增加，模型性能不会呈现规律性的变化。当特征变量数较少时，可能存在过拟合的情况。

3） 测试结果表明，所创建的随机森林回归模型预测值与实测值的平均绝对误差、平均相对误差随着特征变量数的增加呈下降趋势，特征变量数的增加可在一定程度上提高模型的预测效果。

4） 针对同一组数据，与主成分回归分析法相比，随机森林回归模型平均相对误差降低了14.29%，预测效果更好，且原理更简单、调参更容易、计算速度更快，能够为矿井回采工作面瓦斯涌出量预测提供有力的理论支撑。