基于改进鸽群算法的稀疏阵列优化问题研究

孙 丹,梁复台,张琬婷,

(1.解放军31411部队,辽宁 沈阳 110000;2.空军预警学院,湖北 武汉 430019)

0 引 言

矩形平面稀疏阵列天线近年来一直备受关注。矩形平面稀疏阵列天线是指从均匀排布的矩形相控阵天线中按照一定的比例剔除掉部分阵元[1]。天线阵列为了减小阵元间的互耦,阵元间距必须满足一定的约束(比如不小于某一给定值),但往往带来栅瓣问题,因此常采用稀疏阵列天线。虽然矩形平面稀疏阵列天线仍具有栅瓣或高旁瓣等缺点[2],但是可以通过对平面稀疏阵列阵形优化,达到比均匀满阵天线更低的副瓣电平或更高的角度分辨率[3]。同时,稀疏阵列所需阵元数目更少,阵列天线成本和重量更低,具有结构简单和成本低等优点[4]。

目前,在平面稀疏阵列阵形优化中获得全局最优峰值副瓣电平(PSLL)的唯一方法是穷举法;但是,随着稀疏阵列阵元的增加,穷举法的计算量呈指数增长[5]。因此,学者们提出了各种各样的群智能优化算法来确定稀疏阵列的阵型。群智能优化算法是一种随机优化技术,为解决最优化问题开创全新局面,其本质是仿生——对自然界中生物群体行为的模仿,比如蜂群、狼群、蚁群等。其最大的优点是不用深入分析问题的本质,可依赖算法仿生的群体行为对可行解域进行快速全面的搜索,得到满意解,同时具有较强的稳定性。近年来,群智能优化算法被证实具有很强的竞争力和较好的全局搜索能力,因此,群智能优化算法越来越受到学者们的关注,许多学者根据自然界中生物的社会行为,提出或改进了群智能优化算法。例如:鸽群优化算法(PIO)[6]、麻雀搜索算法[7]、灰狼优化算法[8]、鲸鱼优化算法[9]等。

针对该问题,使用较多的群智能优化算法主要有粒子群优化算法(PSO)[10]、遗传算法[11]、模拟退火算法[12]等。本文提出了一种改进鸽群优化算法对阵元间距为半波长、最大阵元数目为400的矩形平面稀疏阵列阵型进行优化。仿真结果证明了与PSO和PIO相比,改进鸽群优化算法有更好的有效性。

1 稀疏阵列数学模型

1.1 矩形平面稀疏阵列方向图

在YOZ平面有一个由M×N个阵元组成的矩形平面稀疏阵列天线,沿y方向(横向)的N个阵元以间距dy均匀排列,沿z方向(纵向)的M个阵元以间距dz均匀排列,如图1所示。

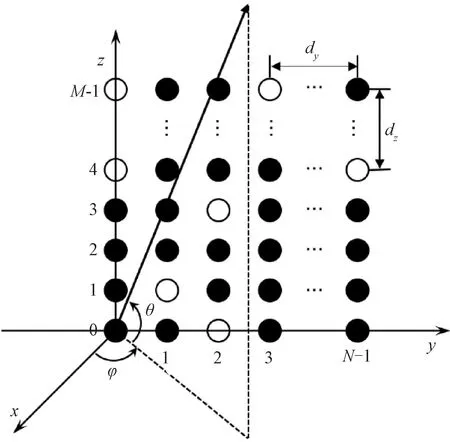
图1 矩形平面稀疏阵列示意图

因此,可以用(m,n)来表示阵列中任意一个阵元的位置,其中,0≤m≤M-1,0≤n≤N-1。设来波方向的俯仰角为θ,方位角为φ,天线俯仰角波束指向为θ0,方位角波束指向为φ0,自由空间相位常数k=2π/λ。

矩阵A表示阵列中各阵元的开关状态:

(1)

式中:amn表示(m,n)位置的阵元开关状态,amn=1表示(m,n)位置的阵元开启,amn=0表示(m,n)位置的阵元关闭。

矩阵B表示阵列中各阵元的激励:

(2)

式中:bmn表示(m,n)位置的阵元的激励大小,且0≤bmn≤1。

设矩阵C为:

(3)

式中:当cmn=0时表示(m,n)位置的阵元关闭,当cmn>0时表示(m,n)位置的阵元开启,cmn的值表示该阵元激励大小,且cmn≤1。

设:

u=dz(sinθ-sinθ0)

(4)

v=dy(cosθsinφ-cosθ0sinφ0)

(5)

因此,可以给出该稀疏阵列的方向图函数为:

(6)

1.2 优化模型

本文稀疏阵列优化的目的是使阵列方向图PSLL最小,首先需要构建优化模型,在θ∈(-90°,90°),φ∈(-90°,90°)的半球面的非主瓣区域内搜索最大旁瓣,定义非主瓣区域为S1,根据PSLL定义,适应度值函数为:

(7)

为得到最小PSLL,所以最后的优化模型为:

(8)

2 群体智能算法

2.1 粒子群算法

粒子群算法从自然界中的鸟群、兽群和鱼群等群体进行迁移活动而来。在群体活动中,群体中的每个个体都会受益于所有群体成员所发现和累积的经验,在求解优化问题时体现出了很好的效果。在粒子群算法中,每个粒子的位置代表优化问题的一个解,每个粒子根据自身的运动经验和群体中其他成员的运动经验来调整自己的运动速度和方向,以向更好的位置移动,即搜索到更好的解。

设Q维的搜索空间内,群体个数为NP,任意一个粒子i的速度vi和位置xi都是Q维向量,分别为:

vi=(vi1,vi2,vi3,…,viD)

(9)

xi=(xi1,xi2,xi3,…,xiD)

(10)

粒子i速度vi和位置xi的第j维元素更新公式为:

vij(t+1)=wvij(t)+c1r[p-xij(t)]+

c2r[pi-xij(t)]

(11)

xij(t+1)=xij(t)+vij(t+1)

(12)

式中:t为迭代次数;w为惯性权重;c1为粒子群体学习因子;c2为粒子个体学习因子;r为[0,1]范围内的随机数;p为群体最优解;pi为粒子i的最优解。

2.2 鸽群算法

鸽群有出众的导航能力,影响鸽群导航能力的主要因素有磁场、太阳和地貌景观。而段海滨等人于2014年提出的鸽群算法[6]就是模拟鸽群出众的导航能力设计出来的群智能优化算法。鸽群算法主要由2个阶段组成:地图和指南针算子阶段、地标算子阶段。

地图和指南针算子阶段是模仿太阳和地球磁场这2种导航工具对鸽子的作用。鸽子通过磁感来感受磁场,从而在脑海中绘制地图,并把太阳当作指南针来调整方向。随着鸽群越来越逼近目的地,会逐步减少对太阳和磁性粒子的依赖。在此阶段,鸽群算法类似于粒子群算法,每只鸽子同样由其位置信息和速度信息表示。地标算子阶段主要是提升了算法的探索能力,地标算子模仿导航工具地标对鸽子的影响。当鸽群接近目的地时,会依靠临近地标进行导航。如果某只鸽子熟悉地标,那么会径直飞向目的地;反之,如果不熟悉地标并且远离目的地的情况下,该只鸽子会跟随熟悉地标的其他鸽子飞行,从而到达目的地。

设Imax为最大迭代次数,RN为地图和指南针算子阶段迭代次数与最大迭代次数的比,在Q维的搜索空间内,鸽子群体个数为NP,任意一个鸽子i的速度vi和位置xi都是Q维向量。迭代次数t在[0,Imax·RN]内为地图和指南针算子阶段,该阶段鸽子i速度vi和位置xi的第j维元素更新公式为:

vij(t+1)=vij(t)e-R·t+nrand·(xj(t)-xij(t))

(13)

xij(t+1)=xij(t)+vij(t+1)

(14)

式中:t为迭代次数;R为罗盘算子;nrand为[0,1]内的均匀随机数;xj为鸽群最优鸽子位置的第j维元素。

迭代次数t在[Imax·RN+1,Imax]内为地标算子阶段,该阶段根据鸽群所代表的PSLL进行排序,将鸽群等分为2组,每次迭代中舍弃掉PSLL较差的那组鸽群,并根据有较优PSLL的鸽群位置和PSLL作为参数,供自己确定新位置。第i个鸽子位置xi的第j维元素更新公式为:

(15)

(16)

xij(t+1)=xij(t)+nrand·(Xcj(t)-xij(t))

(17)

2.3 改进鸽群算法

传统鸽群算法很容易“早熟”,会造成陷入局部最优的缺陷。为了解决该问题,本文从地图和指南针算子阶段和地标算子阶段对传统鸽群算法进行优化。

2.3.1 地图和指南针算子阶段

一方面,传统鸽群算法地图和指南针算子阶段的本质是仅以鸽群中最优位置的鸽子作为鸽群的搜索方向,有“早熟”造成陷入局部最优的可能性。因此,仿照粒子群的原理,引入鸽群个体历史最优解,以多个方向维度去寻找最优结果,有利于跳出局部最优。

另一方面,传统鸽群算法的罗盘算子R是固定的,在地图和指南针算子阶段,随着迭代的次数增加,上次迭代速度对本次迭代的影响越来越小,使该算法在迭代后期极其不易跳出局部最优。因此引入一个随机因子,使罗盘算子R随机变化,加强其跳出局部最优的可能性。

所以,本文改进鸽群算法在地图和指南针算子阶段的更新公式为:

vij(t+1)=vij(t)e-[Rmin+nrand(Rmax-Rmin)]t+

nrand·(xj(t)-xij(t))+

nrand·(xij(t)-xij(t))

(18)

xij(t+1)=xij(t)+vij(t+1)

(19)

式中:t为迭代次数;Rmax为最大罗盘算子;Rmin为最小罗盘算子;nrand为[0,1]内的均匀随机数;xj为鸽群最优鸽子位置的第j维元素;xij为鸽群中第i个鸽子的历史最优位置的第j维元素。

2.3.2 地标算子阶段

传统鸽群算法在地标算子阶段中每次迭代都会使鸽群数目衰减一半,过早地舍弃了鸽群中较差的个体,造成了种群多样性的丧失,导致“早熟”造成陷入局部最优。

所以,本文改进鸽群算法在地标算子阶段,不再舍弃鸽群中较差的个体,而是直接更新它们的位置。在该阶段,根据鸽群所代表的PSLL进行排序,将鸽群等分为2组,较优PSLL的鸽群位置按照地图和指南针算子阶段进行更新,并将其更新前的位置和PSLL作为参数,供较差的一组确定自己的新位置。较差个体组中第i个鸽子位置xi的第j维元素更新公式为:

(20)

(21)

3 仿真设计与分析

3.1 参数设置

本节仿真主要使用粒子群算法、传统鸽群算法、改进鸽群算法对阵元间距为半波长、最大阵元数目为400的矩形平面稀疏阵列阵型进行优化。

来波方向的俯仰角θ与方位角φ的取值范围为[-90°,90°],仿真步进为1°,其他矩形平面稀疏阵列参数如表1所示。

表1 矩形平面稀疏阵列参数

为了更好地比较3种智能算法对平面稀疏阵列阵形优化的好坏,使种群个数与迭代最大次数一致,并使用同一个随机生产的初始值开始迭代。

粒子群算法参数如表2所示。

表2 粒子群算法参数

传统鸽群算法参数如表3所示。

表3 传统鸽群算法参数

改进鸽群算法参数如表4所示。

表4 改进鸽群算法参数

3.2 仿真分析

图2为粒子群算法、传统鸽群算法、改进鸽群算法对平面稀疏阵列天线进行阵形优化时,寻到最优峰值旁瓣电平随迭代次数的变化图。

图2 不同算法下最优PSLL随迭代次数的变化图

观察各算法迭代过程,粒子群算法与传统鸽群算法的搜索结果与迭代曲线较为接近,在-18 dB左右处陷入局部最优解;虽然3种算法的前期迭代速度相差不大,但是相比于粒子群算法、传统鸽群算法,改进鸽群算法有更优搜索能力,不易陷入局部最优解,针对平面稀疏阵列天线阵形优化有更优的效果。

图3为使用改进鸽群算法对平面稀疏阵列天线进行阵形优化结果的三维方向图。方向图主瓣电平为0 dB,最大旁瓣电平为-19.35 dB。

图3 改进鸽群算法阵列三维方向图

图4为使用改进鸽群算法对平面稀疏阵列天线进行阵形优化结果。式(3)矩阵C的取值,当cmn=0时,表示(m,n)位置的阵元关闭;当cmn>0时,表示(m,n)位置的阵元开启。cmn的值表示该阵元激励大小,且cmn≤1。

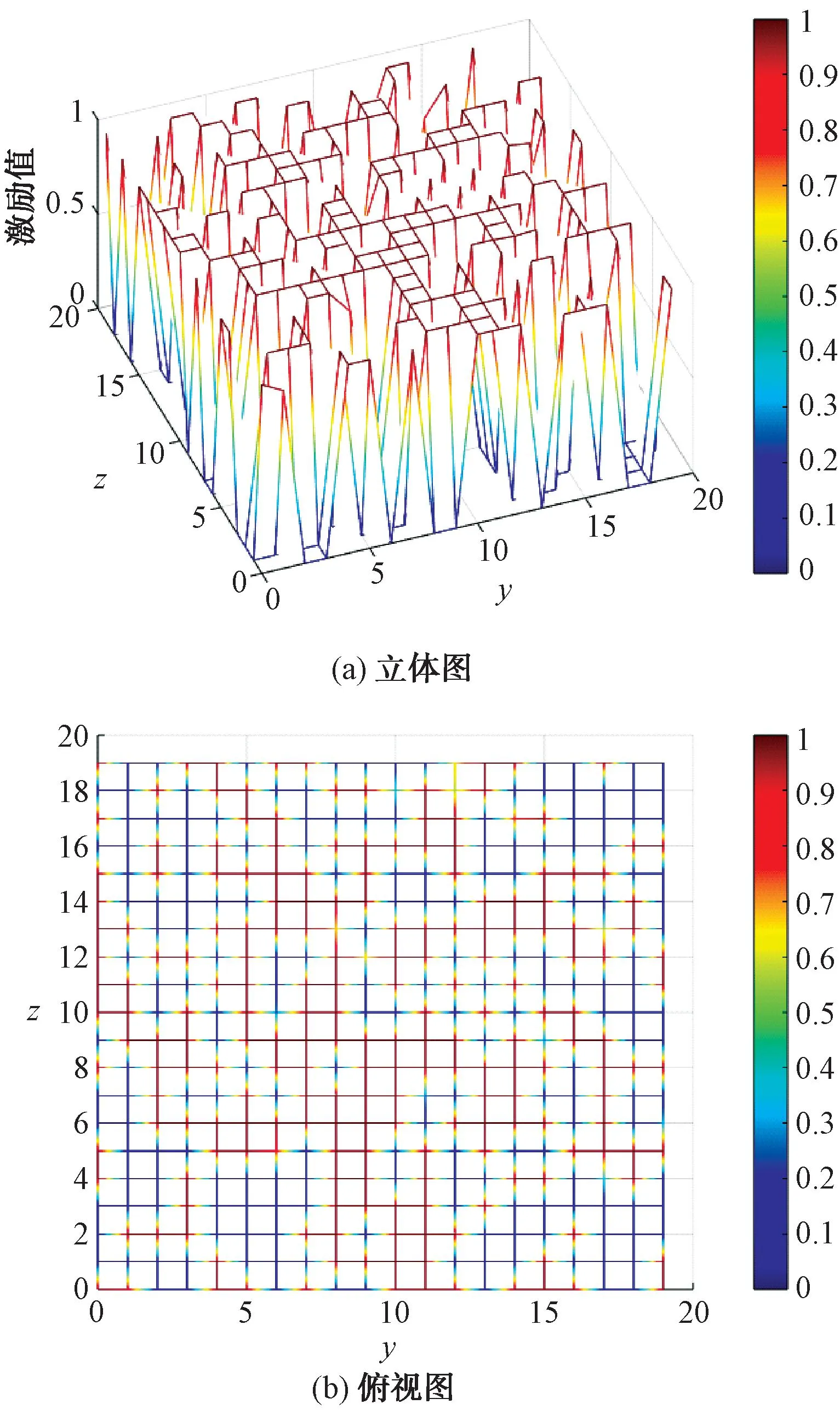
图4 改进鸽群算法阵形优化结果图

通过试验比较可以看出,改进的鸽群算法有更优的搜索能力,适用于平面稀疏阵列天线阵形优化问题。

4 结束语

针对平面稀疏阵列阵形优化算法搜索策略单一问题,本文提出了一种改进鸽群算法。在地图和指南针算子阶段,一方面,引入鸽群个体历史最优解,以多个方向维度去寻找最优结果;另一方面,引入一个随机因子,使罗盘算子R随机变化,加强跳出局部最优的可能性。在地标算子阶段,不再舍弃鸽群中较差的个体,而是以较优个体的位置和PSLL对其位置进行更新,这样不会造成种群多样性的丧失,加强跳出局部最优的可能性。仿真结果证明了与粒子群算法、传统鸽群算法相比,改进鸽群优化算法针对平面稀疏阵列阵形优化问题有更好的效果。