Perceptual Optimization for Point-Based Point Cloud Rendering

YIN Yujie, CHEN Zhang

(School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China)

Abstract: Point-based rendering is a common method widely used in point cloud rendering. It realizes rendering by turning the points into the base geometry. The critical step in point-based rendering is to set an appropriate rendering radius for the base geometry, usually calculated using the average Euclidean distance of the N nearest neighboring points to the rendered point. This method effectively reduces the appearance of empty spaces between points in rendering. However, it also causes the problem that the rendering radius of outlier points far away from the central region of the point cloud sequence could be large, which impacts the perceptual quality. To solve the above problem,we propose an algorithm for point-based point cloud rendering through outlier detection to optimize the perceptual quality of rendering.The algorithm determines whether the detected points are outliers using a combination of local and global geometric features. For the detected outliers, the minimum radius is used for rendering. We examine the performance of the proposed method in terms of both objective quality and perceptual quality. The experimental results show that the peak signal-to-noise ratio (PSNR) of the point cloud sequences is improved under all geometric quantization, and the PSNR improvement ratio is more evident in dense point clouds. Specifically, the PSNR of the point cloud sequences is improved by 3.6% on average compared with the original algorithm. The proposed method significantly improves the perceptual quality of the rendered point clouds and the results of ablation studies prove the feasibility and effectiveness of the proposed method.

Keywords: point cloud rendering; outlier detection; perceptual optimization; point-based rendering; perceptual quality

1 Introduction

With the increasing demand for stereoscopic visual effects and immersive experiences, 3D point clouds are emerging as one of the primary threedimensional data in various areas. Point clouds are usually generated from sensor data, e.g., triangulation and Time-of-Flight (ToF)[1]. A point cloud is a set of points in a given coordinate system representing information about a scene or an object, often complemented with per-point attributes. This set of points may define the shape of real or computer-generated objects or even complex scenes[2]. A point cloud has both geometric and attribute features, where the geometric features reflect the number of points in the point cloud in relation to their position, while the attribute features can contain additional information such as the color,grey value, average vector and reflectivity of the points. 3D point clouds[3-5]have found broad applications in manufacturing, construction, environmental monitoring, navigation, animation, rendering, etc.[6]However, various distortions may be introduced during the acquisition, compression[7], transmission, storage, and rendering processes of point clouds, leading to degraded perceptual quality[6]. Improving the Quality of Experience (QoE)[8]of point clouds is very important for related applications.

Point cloud rendering is the process of producing a visual representation that can be consumed by users using an available display, e.g., conventional 2D, stereo, auto-stereoscopic,head-mounted displays, etc.[9]The rendering process has a significant impact on the quality perceived by the user[10]. Point clouds have many properties that differ from traditional video images. First, a point cloud is an unordered collection. Second, a point cloud is unstructured, and the relative positions between individual neighboring points are not the same, which means that even finding neighboring points requires traversing all the points in the point cloud. Finally, point clouds are nonuniform. They are usually obtained by sampling a single object, and the densities of points in different regions of the same point cloud may vary significantly[11]. These characteristics of point cloud data pose new requirements and higher challenges to the algorithms for point cloud rendering.

Currently, two main categories of rendering methods are commonly used for point clouds[11]. One is mesh-based rendering, which constructs a polygonal mesh through surface reconstruction algorithms, e.g., Poisson surface reconstruction[12].These rendering methods can construct a completely closed surface, but the results highly depend on the reconstruction algorithm, and human intervention may be required to reconstruct complex surfaces. As the object in 3D may be complicated, extensive computation is generally involved[13]. The other category is point-based rendering, which achieves rendering results by turning points into the base geometry with area (e.g., circles, spheres, cubes, etc.). The point-based methods are low in computation and easy to implement, but it is necessary to define the size of the base geometry in advance.Otherwise, empty spaces will appear between points (size too small) or aliasing artefacts (size too large). Generally speaking, point-based rendering is easier to perform in comparison with a polygonal mesh representation where surface reconstruction and interpolation are usually needed[10].

Point-based rendering is a common method widely used in point cloud rendering. In Ref. [10], JAVAHERI et al. used the average Euclidean distance ofN(N=10) nearest neighboring points to determine the rendering radius of points in their research work of point clouds, thus solving the problem of the requirement of artificially defining the size of the base geometry in point rendering and avoiding the empty spaces between points.

In point cloud rendering, the rendering radius is generally determined by the nearest neighbors. However, this approach faces challenges when there are outliers. Since the rendering radius is determined by the nearest-neighboring points, the rendering radius of the outliers far away from the central region of the point cloud sequence may be set as a very large value, which impacts the subjective quality. The above problem is illustrated in Fig. 1. The rendering radius of the outliers can seriously affect the subjective quality of the rendered point cloud sequence. Therefore, it is important to filter out the outliers and set an appropriate rendering radius before rendering to improve the perceptual quality of the point cloud sequence.

To solve the problem of poor perceptual quality in pointbased rendering due to the large rendering radius of outlier points, we propose an algorithm for point cloud rendering through outlier detection to optimize the perceptual quality of rendering. The algorithm constructs outlier detection conditions by combining local and global geometric features. During rendering, the rendering radius of outliers is set to the minimum. By doing so, the proposed method realizes the perceptual optimization of point cloud rendering and improves the perceptual quality after point cloud rendering.

The main contributions of this paper are as follows:

1) We propose an outlier detection algorithm with low complexity. The proposed method uses global and local geometric features to detect outliers in the sequence.

2) We apply the outlier detection algorithm to point cloud rendering to optimize the perceptual quality of the point rendering. Compared with the original rendering algorithm, our method improves both the perceptual quality of the rendered point cloud and the objective quality. The ratio of peak signalto-noise ratio (PSNR) improvement is about 3.6%.

The rest of this paper is organized as follows. Section 2 introduces the rendering algorithm with outlier point detection.Section 3 shows the rendering results of this rendering algorithm and examines the algorithm’s performance in terms of both objective and perceived quality. The paper is summarized in Section 4.

2 Rendering Based on Outlier Detection

2.1 Overview

Suppose the coordinates of thei-th point in the point cloud sequence are (xi,yi,zi),i= 1,2,…,M. The coordinates of the nearestNneighboring points (including the point itself)are,n= 1,2,…,N, whereistands for the point to be detected in the point cloud sequence andnstands for thenth neighboring point of the point to be detected.

▲Figure 1. Illustration of outliers in rendering (rendering primitive is a circle)

The average Euclidean distance of theNnearest neighboring points is taken as the rendering radius of the point. Thus the rendering radiusriof thei-th point is:

As can be seen from the above equation, outlier points far away from the central region of the point cloud sequence will have too sizeable Euclidean distance from their nearest neighbors, and thus, the rendering radiusriwill be too large, which in turn results in an impaired subjective perception of the quality of the rendered point cloud sequence.

In order to solve the problem of too large a rendering radius of outlier points in the above method, we need to add a process of detecting and determining outlier points before rendering each point in the point cloud sequence. We determine whether each point is an outlier, filter the outlier points and change their rendering radii. For the outlier points, the minimum rendering radius is used. For the non-outlier points, the radius of the nearest neighbor renderingriis used as shown in Eq. (1).

Outlier detection is a commonly used detection method in data analysis and processing, often used to identify abnormal samples or points in outlier states that significantly deviate from the central region of the sequence. Many outlier mining methods can be categorized into five groups: distributionbased, depth-based, clustering-based, distance-based, and density-based[14-15]. Commonly used detection methods are distance detection-based K-nearest neighbor algorithms, isolated forest methods, clustering-based DBSCAN algorithms[16],LOF algorithms[17], supervised or unsupervised algorithms based on machine learning[18], and distribution-based and density-based outlier detection[19]. However, the above methods have the disadvantages of high time complexity, poor detection results in high-dimensional sparseness, and insignificant mathematical geometric features.

Since determining the rendering radius in terms of the nearest neighboring points is through geometric features, detecting outlier states at each point based on geometric features is reasonable. To ensure the accuracy of detection, global and local geometric features construct a comprehensive judgment condition to quickly check and judge whether the current point is in an outlier state.

The implementation complexity of the detection method needs to be as low as possible for rendering. So we use discrete point detection techniques based on statistical distributions, combining local and global geometric features to judge outliers. This is a method that has solid probabilistic statistical theory support. After modeling, it does not require modelbased data, and only the minimum amount of information describing the model needs to be stored, which can effectively reduce the data storage.

2.2 Construction of Outlier Judgment Conditions

The basic principle of the algorithm for point cloud rendering through outlier detection in this paper is to determine whether the detected point is in an outlier state by judging whether the point satisfies the distribution type of the dataset and, thus, whether the point is in an outlier state. Assuming that the data satisfy the condition of obeying normal distribution,p0belongs to the datasetp, and the mean and standard deviation of this dataset areandσ, respectively. The judgment criteria of outlier detection are shown in Eq. (2)[20]. When Eq. (2) is not satisfied, the pointp0is determined to be in an outlier state.

From Eq. (1), we can see that the rendering method based on the nearest neighbor distance determines the size of the rendering radius of each point in the point cloud sequence by the geometric density feature in the local area. Therefore, the geometric features of outlier points are also chosen as density features in this method, i.e., the rendering radius is calculated based on the nearest-neighbor distance.

Let the rendering radius of the nearestN(N= 10) neighbors of the detection point be, the mean value of the local geometric density feature beE(r), and the standard deviation beσr.E(r) andσrare calculated in Eqs. (3) and (4).

Combining the outlier judgment criteria, we substitute the rendering radius data into Eq. (2), and the outlier judgment criteria for the local geometric feature construction are shown as follows[12]:

When the detection point does not satisfy the local determination condition of the above equation, it is determined that the detection point is in the outlier state.

Since the number of detected points in the point set covered by the local geometric features is small, only local features are not enough to detect outliers. In addition, the local geometric features easily fall into the local small sample situation. When the points included in the local geometric features are all outliers, the local judgment condition criteria will fall into local condition satisfaction, resulting in outlier detection failure.Therefore, it is limited to judging whether the detected points are in an outlier state only by local geometric conditions, and it is necessary to expand the geometric features and the capacity of the point set in the judgment conditions. Therefore, the global geometric features are added as a judgment condition for outlier detection.

Let the global geometric feature beR, which is calculated in Eq. (6), whereMis the number of bits in the global geometric point set.

In order to reduce the complexity of the algorithm implementation, the actual rendering process can use the cumulative means as a global geometric feature, which is calculated in Eq. (7).

wheremis the ranking bit of the current detection point in the rendering process.

Therefore, based on Eq. (2), the criteria for determining outlier points for global geometric feature construction are:

When a detection point does not satisfy any of the determination conditions of the global condition and the local condition, the detection point is judged to be an outlier.

2.3 Rendering Through Outlier Detection

Before rendering the points in the point cloud sequence, the outlier status is detected for each point. First, we input the points in the point cloud sequence. Since the point cloud is disordered, we need to arrange the disordered points in the point cloud sequence in an orderly manner to facilitate fast and efficient retrieval. Therefore, the k-dimensional (KD)-tree[21]is constructed with the detection points as the core, and the points are divided according to the tree structure to facilitate the subsequent nearest neighbor search. In constructing the KD-tree, we follow the method in Ref. [20] to transform the distribution of point sets in the point cloud sequence into a normal distribution. Thus, the prerequisite assumption of normal distribution of data in Eq. (2) is satisfied. The global geometric featureRis calculated according to Eq. (7). The points in the point cloud sequence are traversed according to the order in the KD-tree, and the rendering radiusriis calculated according to Eq. (1) after searching theNnearest neighboring points of the current detection point. The local feature valuesE(r) andσrare calculated according to Eqs. (3) and (4). The global and local conditions are judged according to Eqs. (5) and (8) in turn, and if either of the two judging conditions is not satisfied, the detected point is judged to be in the outlier state. The rendering radiusriof the point in the outlier state is set to the minimumrmin. When the detected point satisfies both local and global detection conditions,the rendering radiusriis not changed. Finally, the detected point rendering radiusriis passed to the renderer for the rendering of each point by the renderer. The specific flow of the rendering algorithm through outlier point detection is shown in Fig. 2.

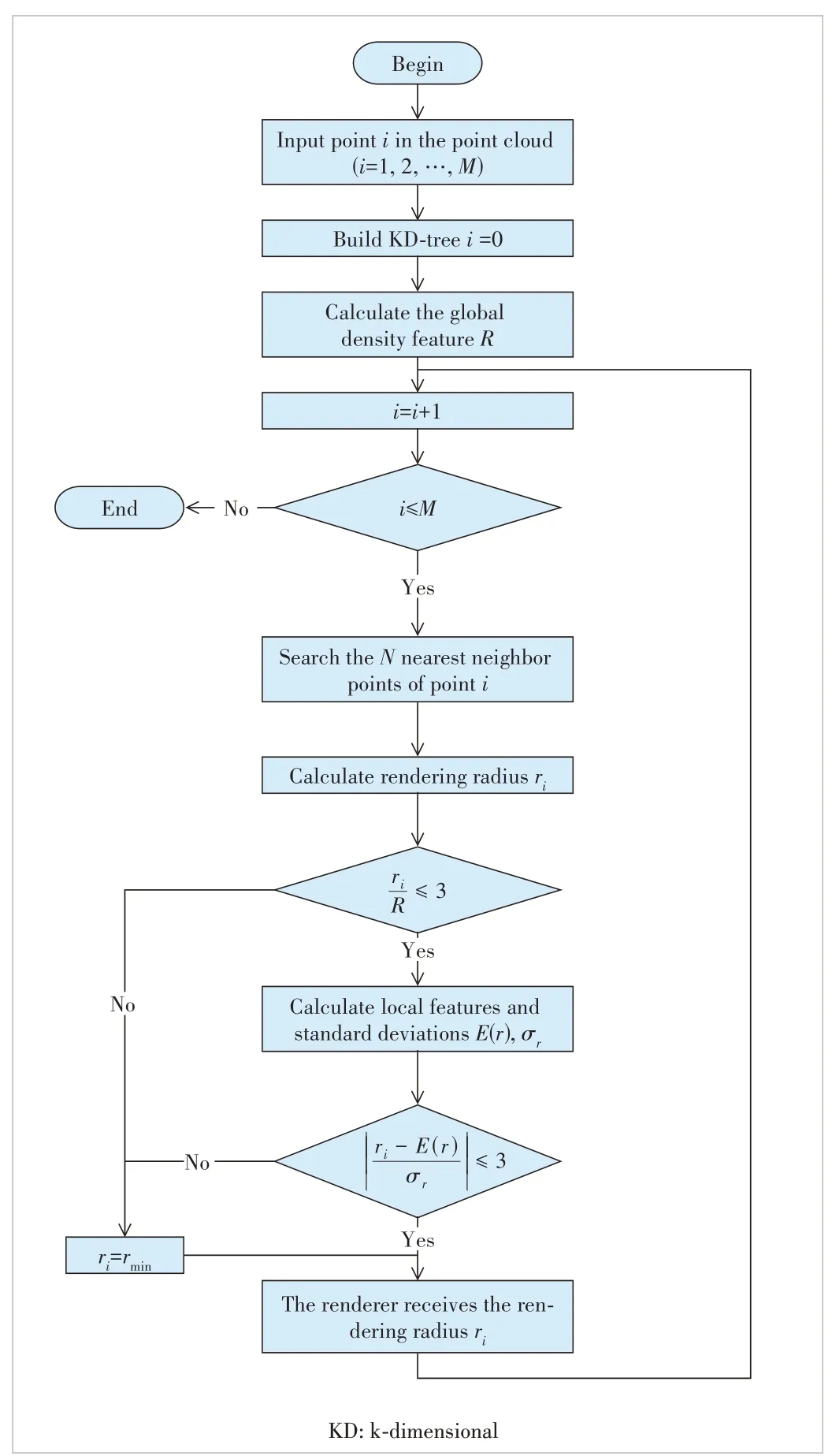
▲Figure 2. Flow chart of proposed rendering through the outlier detection

3 Experimental Results

3.1 Point Cloud Sequence Selection

We use ten static point clouds to examine the performance of the proposed method in terms of objective and perceptual quality. Fig. 3 shows a thumbnail of the point cloud sequences. Table 1 shows the detailed information of each point cloud sequence.

3.2 Subjective and Objective Results

The effect of the rendering through outlier detection is first evaluated by conducting a subjective comparison before and after outlier optimization. Take Head’s character point cloud sequence and Phil’s object point cloud sequence as examples. Figs. 4 and 5 show the subjective comparison effects of the above two point cloud sequences using the original point-rendering[10]and the proposed method. It can be found that the rendering radius of outlier points far from the main sequence area is significantly reduced after outlier detection and rendering, and the perceptual quality of the point cloud sequence is improved.

▲Figure 3. Point cloud sequence thumbnail

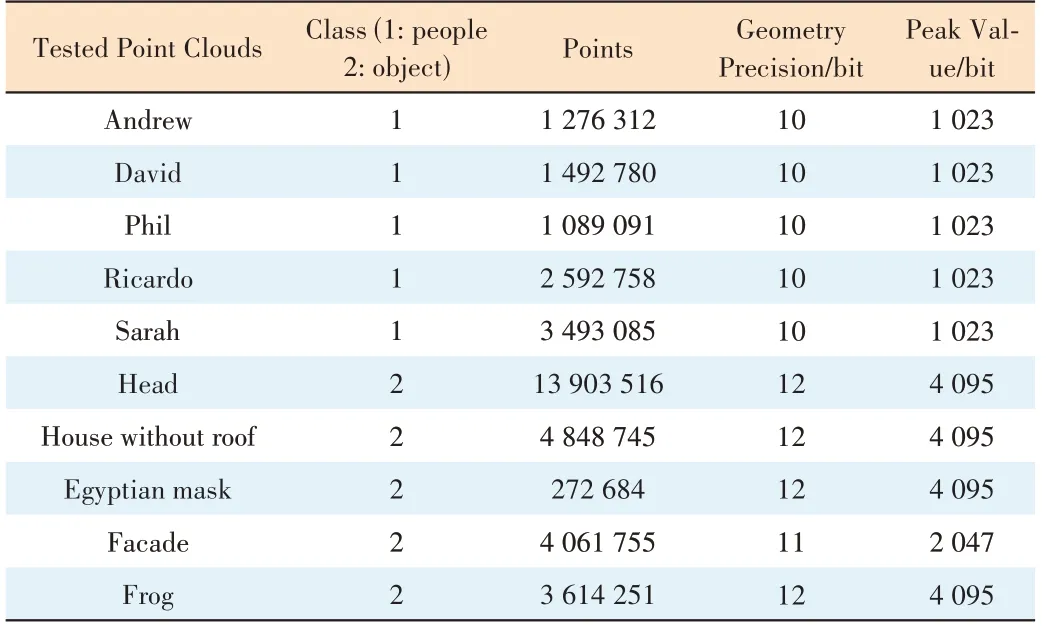
▼Table 1. Point cloud sequence details

▲Figure 4. Point cloud Head before and after optimization comparison diagram

▲Figure 5. Point cloud Phil before and after optimization comparison diagram

We also compress the original point cloud sequence and calculate the PSNR using the original point rendering[10]and the proposed method. The improvement of PSNR using the proposed method is utilized to react to the effectiveness of rendering based on outlier detection.

In terms of point cloud compression, since outlier point detection does not target the attribute features of the point cloud sequence, the original color attributes are not compressed, and the original point cloud sequence attributes are kept lossless.Regarding geometric compression, we choose three geometric quantization parameters with large discretization, namely {1/10,1/2, 15/18}, to verify the effectiveness of the proposed algorithm under different degrees of geometric compression in geometry point cloud compression (G-PCC).

To compute PSNR, we project each point cloud sequence to the three planes of the point cloud enclosing the box to form three views of the point cloud view. We render the original uncompressed sequence of the point cloud sequence through PccAppRendererV6.0 with the rendering radius set to 1.0 to obtain the reference view of the point cloud sequence. The quantized distortion images of each point cloud sequence before and after optimization are obtained in turn, and the mean squared error (MSE) and PSNR are calculated from the reference image and distortion image as shown in the following equations.

where the image pixels arem*n,I(i,j) represents the reference point cloud sequence view pixel points,K(i,j) represents the quantized distortion point cloud sequence view pixel points, and MAX denotes the possible maximum pixel value of the image.

The improvement ratios of PSNR of the proposed method are shown in Table 2.

As can be seen from Table 2, the PSNR of each point cloud sequence has been improved using the proposed method regardless of the size of the geometric quantization parameters. As the geometric quantization parameter increases, more points are retained in the point cloud sequence. Therefore, for the same point cloud sequence, the advantage of the proposed method will be more significant with the increase in the density of the point cloud sequence. The reasons for the above phenomenon are that sparse point clouds are more likely to produce outliers, and the original point rendering will have worse subjective perception quality so that the PSNR improvement ratio will be more pronounced. After rendering through outlier detection, the PSNR of each point cloud sequence is improved. Specifically, the average PSNR improvement ratio is 3.6%.

3.3 Time Complexity

Specifically, we record the rendering time in the experiment in Section 3.2. Then we calculate the ratio of increased rendering time spent for the original rendering and the proposed rendering, as shown in Eq. (10).

whereTris the ratio of increased rendering time,T1is the rendering time using the proposed method, andT0is the original rendering time. The calculation results are shown in Table 3.

Observing the results, we can conclude that the rendering time is increased by 5.8% on average due to the added outlier detection.

3.4 Ablation Studies

To evaluate the effectiveness of using the local and global geometric features in outlier detection, we conduct studies using three-point cloud sequences: Andrew, David and Phil. For quantization, we still use the same geometric quantization parameters as set in Section 3.2: {1/10,1/2,15/18}.

The local and global geometric features are respectively used and then compared with the original rendering without optimization. For performance evaluation, the individual point cloud sequences are also projected onto the three planes of the point cloud enclosing the box to get the view from the corresponding perspective. The PSNR of the point cloud sequences under each rendering method is calculated from the undistorted point cloud sequence image and distorted point cloud sequence image. Finally, we calculate the average PSNR improvement compared with the original rendering method, as shown in Table 4.

It is seen that both local and global geometric features contribute to improving the quality of the point cloud sequence.However, both individual features are less effective than using both. In addition, the local geometric feature contributes more compared with the global geometric feature.

▼Table 3. Ratio of increased rendering time

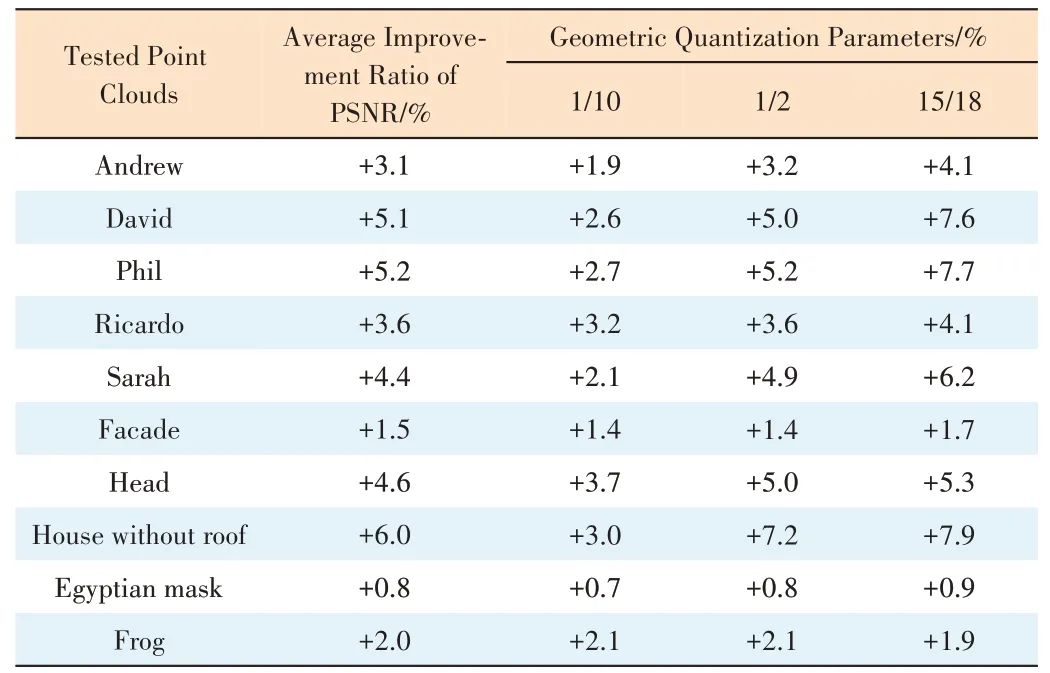
▼Table 2. PSNR improvement ratio before and after optimization with geometric quantization parameters

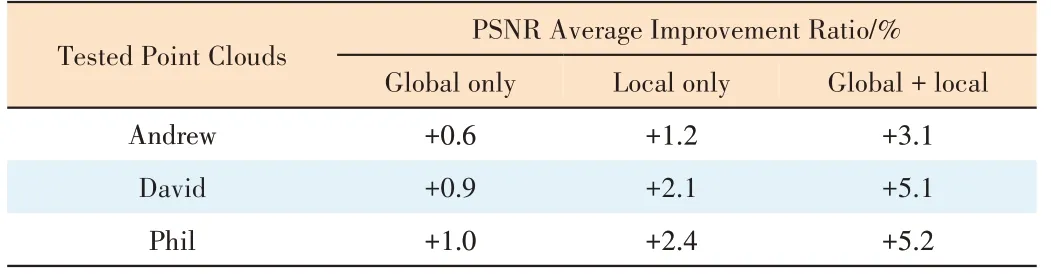
▼Table 4. Average improvement ratio of PSNR in ablation studies

4 Conclusions

In this paper, we focus on optimizing the perceptual quality of point cloud rendering through outlier detection. We evaluate the performance of the proposed method in terms of perceptual quality and the PSNR improvement ratio. In addition,we evaluate time complexity analysis and perform ablation studies. Future work may include applying other methods to outlier detection in rendering to improve the perceptual quality after point cloud rendering.