限制性支撑树最大容量扩张问题

杨子兰，杨惠娟，李 睿*

（1.丽江文化旅游学院信息学院，云南丽江 674199；2.昭通学院数学与统计学院，云南昭通 657000）

随着互联网的不断发展，人们的生活变得越来越网络化、数据化、信息化、智能化，这给通信网络的流量传输能力带来严峻的考验。通信网络分为有线通信网络和无线通信网络。尽管无线通信网络有很好的发展优势，但是有线通信网络一直保持着无可替代的地位。如5G 通信系统中5G 基站的建设需要密集组网，只有光纤通信网络传输技术能为其提供低延时和高带宽的通信，进而实现5G 的顺利入网〔1〕。光纤通信网络属于有线通信网络。有线通信网络往往是大型通信网络的主干道和基础设施，特别是考虑到远程通信的可靠性和稳定性，有线通信具有不可替代的作用〔2〕。有线通信网络在实际应用中将金属材质的导线作为连通载体，可以传输的信息包括文本、文件、图像、音频等〔3〕。

文献〔4〕中作者指出未来网络作为战略性新兴产业的重要发展方向，预计在2030 年将支撑万亿级、人机物、全时空、安全、智能的连接与服务，将重点聚焦在加速业务创新、促进运营商转型、满足工业互联网需求等方面的发展。面对如此庞大的需求压力和发展压力，对现有的网络进行升级变成学者们一直关注的一个热点问题〔5-7〕，然而在现有的网络拓扑结构基础上进行升级，需要消耗资源，升级后网络必须保证通信质量且需要维护，这些都涉及费用问题。因此，如何对现有的通信网络进行科学合理的升级使其满足不断增长的用户流量需求成为一个重点问题。对通信网络容量进行升级不仅要考虑当前用户的流量需求、单位扩容费用以及扩容后的维护费用，还要确保通信质量以及可靠性。与此同时，通信线路太长不仅会增加成本，还会影响通信质量。

结合以上实际情况，为应对高峰期客户的流量需求值，为确保可靠的通信，本研究旨在原有的有线通信网络中找到一个子网络，对子网络进行适当的升级使得整个子网络的流量传输能力尽可能地大。同时，子网络的线路总长不能超过限制值。求总费用最少的网络升级方案，本研究把用户抽象成图论中的顶点，把传输信息的连通载体抽象成图论中的边，提出基于流量需求d 的限制性支撑树最大容量扩张问题（the maximum capacity expansion of spanning tree problem with constraints，MCESTC）。

MCESTC 定义如下：给定一个无向图G=（V，E，l，c，p，p'），其中V 表示图G 的顶点集，E 表示图G的边集合，｜V｜=n，｜E｜=m。对∀e∈E，设l（e）、c（e）、p（e）、p'（e）分别表示边e 的长度权重、容量、单位扩张费用、单位边维护费用，且l（e）、c（e）、p（e）、p'（e）≥0，则p（e）+p'（e）表示边e 上的单位边扩张总费用。考虑在图G 中找到一棵支撑树T 使其满足条件：（1）l（T）＝Σe∈Tl（e）≤L；（2）cap（T）≥d，其中L＞0表示长度权重限制指标值，d＞0 表示当前的流量需求值，cap（T）=min｛c（e）｜e∈T｝。∀e∈E，设△c（e）表示边e 上实际增加的容量，则可建立MCESTC 数学模型如下：

其中，Г 是图G 中所有支撑树构成的集合。

本研究提出的MCESTC 是一种新的扩容模型。与文献〔5-7〕相比较，此模型不同之处在于不仅考虑了扩容后的维护费用，还考虑了整个子网络T 的流量通行能力尽可能大于等于d。文献〔5〕中网络中支撑树的边扩容问题属于本研究的一种特殊情形。

由于限制性支撑树问题（constrained spanning tree problem，CST）是NP-难问题，并且借鉴文献〔5〕中命题1 的证明方法，可证明本研究的MCESTC 和CST 问题是多项式时间等价的，所以本研究MCESTC 问题也是NP-难问题。

本研究的创新点有3 个方面：第一个方面是模型的创新。本研究不仅考虑扩容时的扩张费用，还考虑了扩容后的维护费用，并且还考虑了整个子网络T 的流量通行能力尽可能大，得到的数学模型更符合实际情况。第二个方面是算法的创新。扩容时，传统的删边策略大都采用降低树的长度权重值的策略，整个过程中从不允许树的长度值增加，这样容易出现无解的情况。本研究提出的算法中删边策略采用双边替换策略，允许增加树的长度值，每一次的删边替换中，到底选择增加树的长度值还是选择减少树的长度值的策略，这取决于哪种策略对整个问题的贡献最大。第三个方面是理论应用的创新。本研究恰当地把二部图、完美匹配等理论应用在算法中，效果较好。

1 双边替换基础知识

参考文献〔8〕，对于∀e∈E，设p*（e）=（p（e）+p'（e））△c（e）（权重p*（e）为边e 的总扩张费用），得出以下定义：

定义1 （树边替换）设T 是图G 的一棵树，对于∀e∈T，e'∈GT，假如有T｛e｝∪｛e'｝仍然构成图G 的一棵树，则称（e'，e）为图G 中关于T 的一个树边替换。

定义2 设（e'，e）为图G 中关于T 的一个树边替换。记l（e'，e）=l（e'）-l（e），p*（e'，e）＝p*（e'）-p*（e），则称为长度与费用权重之间的交换比率，即r（e'，e）表示费用权重p*每改变一个单位，长度权重改变r（e'，e）个单位。

定义3 （双边替换）设T 是图G 的一棵支撑树，l（T）＞L，图G 中所有关于T 的树边替换构成的集合记为TER。设△L=L-l（T），△P*=P*OPT-p*（T），P*OPT是MCESTC 问题的一个最优解，则定义以下3种类型的双边替换：

（1）（e'，e）∈TER，假如l（e'，e）＜0，p*（e'，e）≤0或l（e'，e）≤0，p*（e'，e）＜0，则称（e'，e）是第一种类型的双边替换。图G 中所有关于支撑树T 的第一种类型的双边替换构成的集合记为BER-Ⅰ；（2）设（e'1，e1）∈TER，l（e'1，e1）＜0，p*（e'1，e1）＞0，使得＜0，p*（e'，e）＞0｝；设（e'2，e2）∈TER，l（e'2，e2）＞0，使 得（e'2，e2）＝arg则假如r（e'1，e1）≥r（e'2，e2），称（e'1，e1）为第二种类型的双边替换；假如r（e'1，e1）＜r（e'2，e2），称（e'2，e2）为第三种类型的双边替换。图G 中所有关于支撑树T 的第二种类型的双边替换构成的集合记为BER-Ⅱ，关于支撑树T 的第三种类型的双边替换构成的集合记为BER-Ⅲ。

引理1 设T，T ' 是图G 的两棵不同的支撑树，记E1=E（T）E（T '），E2=E（T '）E（T）。构造二部图H=（U，V，E），其中U＝E1，V＝E2，E（H）＝｛（e'，e）｜e∈E1，e'∈E2，T｛e｝∪｛e'｝是一棵支撑树｝〔8〕。

根据引理1，可以得出以下推论。

选择我院2016年1月至2017年8月收治的70例COPD急性加重期患者为研究对象,以随机数字表法分为A组与B两组各35例。A组:男性19例,女性16例,年龄63~84岁,平均年龄(73.5±2.4)岁;COPD急性加重期病程3~16d,平均病程(8.0±1.5)d。B组:男性18例,女性17例,年龄63~85岁,平均年龄(74.0±2.2)岁;COPD急性加重期病程2~15d,平均病程(8.5±1.0)d。两组患者一般资料无明显差异(P>0.05),存在可比性。

推论1 设T 是图G 的一棵支撑树，T* 是MCESTC 问题的最优支撑树，则TT*与T*T 之间存在一个完美匹配P 满足以下条件：

（1）｜P｜=｜TT*｜=｜T*T｜；（2）∀x，y∈P，x≠y，有x∩y=Ø；（3）对于∀（e'，e）∈P，有e∈TT*，e'∈T*T 成立，并且T｛e｝∪｛e'｝是一棵支撑树。

2 MCESTC 问题的算法分析

在文献〔8〕中，作者对CST 问题展开研究，并采用双边替换策略设计一个精确算法求解了边的长度权重取值为1 或0 的CST 问题。本研究提出的MCESTC 问题是一种新的CST 问题且是NP-难的。本研究提出的扩容模型的目标函数与文献〔8〕的目标函数不同，并且模型多了整个子网络T 的流量通行能力尽可能大于等于d 的约束条件，所以研究的问题比文献〔8〕中的CST 问题更复杂，更具挑战性。对于属于NP-难的组合优化问题，有些时候考虑的是能尽快找到一个满意解，因此常常设计一个启发式算法求解该类问题。受文献〔8〕的启发，对文献〔8〕中的双边替换算法进行修改，设计出一个双边替换算法求解扩容模型。具体思路如下：

首先，考虑找到图G 的一棵支撑树T 且保证cap（T）=d。为实现此目标，只需对∀e∈E，当容量c（e）＜d 时，取△c（e）＝d-c（e）；当c（e）≥d 时，取△c（e）＝0 即可。其次，在不考虑长度权重限制的条件下，求出关于权重p*最小的支撑树T。最后，检查T的长度权重值，若l（T）≤L，则T 为MCESTC 问题的一个可行解，算法停止；若l（T）＞L，则采用允许增加T 的长度权重值的双边替换策略，对T 的长度权重进行调整，直到调整后的T 满足l（T）≤L。

当l（T）＞L 时，假如关于支撑树T 的第一类型的双边替换BER-Ⅰ≠Ø，则选择（e'，e）∈BER-Ⅰ，置T=T∪｛e'｝｛e｝，这样能保证不增加总费用p*的前提下，最大可能地减少l（T）的值。假如关于支撑树T 的第一类型的双边替换BER-Ⅰ=Ø，则首先选（e'1，e1）＝arg min（e'，e）∈TER｛r（e'，e）｜l（e'，e）＜0，p*（e'，e）＞0｝，即选择费用权重p*每增加一个单位时，单位长度减少量最大的双边替换（e'1，e1），此时；其次选择（e'2，e2）＝arg max（e'，e）∈TER｛r（e'，e）｜l（e'，e）＞0，p*（e'，e）＜0｝，即选择费用权重p*每减少一个单位时，单位长度增加量最小的双边替换（e'2，e2），此时；最后，在（e'1，e1）与（e'2，e2）之间选择对整体更有利的双边替换（e*'，e*）=arg max｛r（e'1，e1），r（e'2，e2）｝。置T ＝T ∪｛e*'｝｛e*｝，这样即使选到BER-Ⅲ中的双边替换，也能保证在长度权重增加量较少的情况下，减少总费用p*。根据以上思路，允许增加T 的长度权重的双边替换策略具体步骤如下：

第1 步：在图G 中求出关于支撑树T 的树边替换，记TER=｛（e'，e）｜e∈T，e'∈GT 且T｛e｝∪｛e'｝是一棵支撑树｝。把TER 分成BER-Ⅰ、BER-Ⅱ、BER-Ⅲ3 类；第2 步：优先选择BER-Ⅰ中的双边替换进行替换。若BER-Ⅰ=Ø，则在BER-Ⅱ、BER-Ⅲ中选择r（e'，e）值最大的双边替换，即选择双边替换（e*'，e*）=arg max（e'，e）∈TER｛r（e'，e）｜（e'，e）∈BER-Ⅱ或（e'，e）∈BER-Ⅲ｝，置T＝T∪｛e*'｝｛e*｝；第3 步：若l（T）≤L，则T 为MCESTC 问题的一个可行解，算法停止；若l（T）＞L，则重复第2 步，直到调整后的支撑树T 满足l（T）≤L。

当T 是不考虑长度权重限制的条件下关于权重p*最小的支撑树时，显然关于支撑树T 的第一类型的双边替换BER-Ⅰ=Ø 成立。综合以上分析，设计详细的算法步骤如下：

MCESTC 算法：

输出：支撑树T。

第1 步：置p*（e）＝（p（e）+p'（e））△c（e），构造新图G'=（V，E，p*，L，d）。其中∀e∈E，当容量c（e）＜d时，△c（e）=d-c（e）；当c（e）≥d，△c（e）=0。

第2 步：在不考虑长度权重限制的条件下，用Prim 算法〔9〕在新图G'中求出关于权重p*最小的支撑树T。

第3 步：若l（T）≤L，则T 为MCESTC 问题的一个可行解，算法停止；若l（T）＞L，则转第4 步。

第4 步：在图G'中求出关于支撑树T 的树边替换，记TER=｛（e'，e）｜e∈T，e'∈GT 且T｛e｝∪｛e'｝是一棵支撑树｝。把TER 分成BER-Ⅰ、BER-Ⅱ、BER-Ⅲ3 类。

第5 步：优先选择BER-Ⅰ中的双边替换（e'，e）进行替换。若BER-Ⅰ=Ø，则在BER-Ⅱ、BER-Ⅲ中选择r（e'，e）值最大的双边替换，即选择（e*'，e*）=arg max（e'，e）∈TER｛r（e'，e）｜（e'，e）∈BER-Ⅱ或（e'，e）∈BER-Ⅲ｝，置T＝T∪｛e*'｝｛e*｝，转第3 步。

尽管有较多的多项式时间算法可以用来求解最小支撑树问题〔10〕，但是到目前为止，Kruskal 算法〔11〕和Prim 算法是两个比较简单的算法，所以本研究算法中，采用Prim 算法在新图G'中求出关于权重p*最小的支撑树T。

定理1 若MCESTC 问题存在可行解，则算法MCESTC 一定能求出MCESTC 问题的一个满意解，其算法时间复杂度为O（mn2）。

证明：设Ti是算法MCESTC 的第3 步至第5 步经过第i 次循环得到的支撑树，若l（Ti）≤L，则输出可行解Ti，算法停止；否则不断调用MCESTC 算法的第3 步至第5 步，进行双边替换，直到l（Ti）≤L，输出可行解Ti，算法停止。所以若MCESTC 问题存在可行解，则MCESTC 算法能求出MCESTC 问题的可行解。

算法第2 步考虑在新图G'中求出关于权重p*最小的支撑树T，即找出使得目标函数值Σe∈Tp*（e）=Σe∈T（p（e）+p'（e））△c（e）最小的支撑树T，如果l（T）≤L，则T 为MCESTC 问题的最优解，算法停止；若l（T）＞L，则选择对整个问题贡献最大的双边替换进行替换（见算法第5 步），直到l（T）≤L 为止。所以MCESTC 算法能求出MCESTC 问题的一个满意解。

MCESTC 算法中的第1 步构造新图，能在线性时间内完成；第2 步利用Prim 算法，求出关于权重p*最小的支撑树T，时间复杂度为O（n2）；第3 步至第5 步最多循环l（T）次，且l（T）≤n，每一次循环中的算法复杂度主要取决于找到双边替换的复杂度，找到双边替换的复杂度为O（mn）。故MCESTC 算法的总的时间复杂度为O（mn2）。

3 实列

给定无向网络图G=（V，E，l，c，p，p'），见图1。L=11，d=3，G 中每条边上的权重数据见表1。

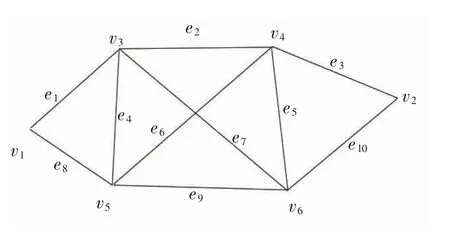
图1 网络G

设p*（e）=（p（e）+p'（e））△c（e），根据MCESTC算法第1 步，得到表1 中△c（e）和p*（e）两行的数据。根据MCESTC 算法第2 步，取v1为初始点，利用Prim算法求得关于权重p*最小的支撑树T，见图2。

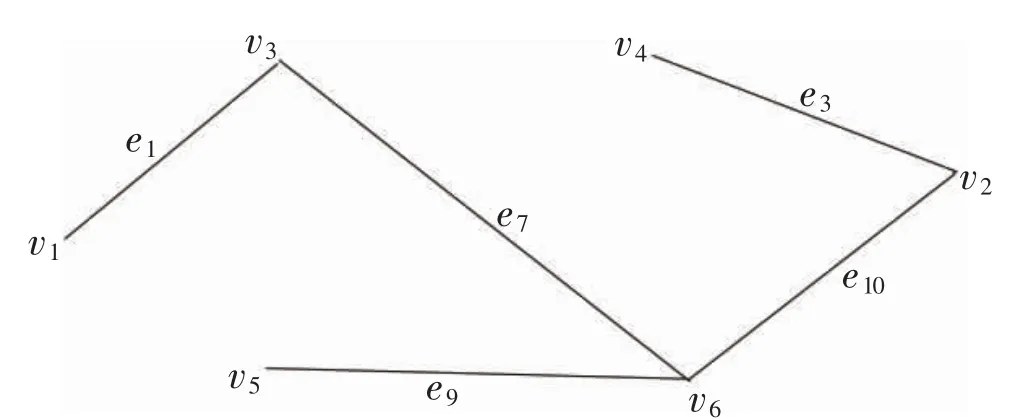
图2 支撑树T

因为l（T）＝22＞L，根据MCESTC 算法第4 步，求出关于T 的双边替换：不存在l（e'，e）＜0，p*（e'，e）≤0 或l（e'，e）≤0，p*（e'，e）＜0 的双边替换，也不存在l（e'，e）＞0，p*（e'，e）＜0 的双边替换，但是存在l（e'，e）＜0，p*（e'，e）＞0 的双边替换：（e2，e7），（e4，e9），（e8，e9），（e6，e9），（e2，e10）。根据MCESTC 算法第5 步有BER-Ⅰ=Ø、BER-Ⅱ=｛（e4，e7）｝、BER-Ⅲ=Ø，置T=T∪｛e4｝｛e9｝，T 的图形见图3。

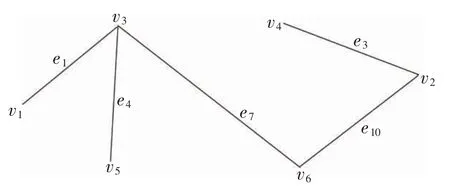
图3 修正的支撑树T

同理，因为l（T）=12＞L，再次调用MCESTC 算法第4 步至第5 步得出BER-Ⅰ=Ø、BER-Ⅱ=｛（e2，e10）｝、BER-Ⅲ=Ø，置T=T∪｛e1｝｛e10｝，此时因为l（T）=11＝L，输T，算法停止。可行解T 的图形见图4。

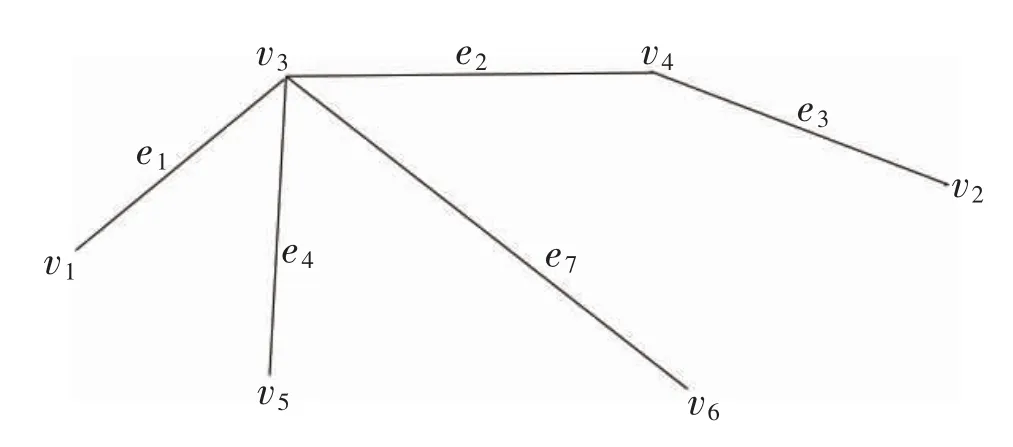
图4 可行解支撑树T