基于GA-PSO-BP的哈尔滨市浅层地下水水位预测模型

王小亮,戴长雷*,闻建伟,齐 悦,章青松

(1.黑龙江大学 寒区地下水研究所,黑龙江 哈尔滨 150080;2.黑龙江大学 水利电力学院, 黑龙江 哈尔滨 150080;3.黑龙江省水文水资源中心,黑龙江 哈尔滨 150001)

地下水资源是赋存于地表松散层孔隙或基岩裂隙中的可以被人类所利用的淡水资源,由于其空间分布广、水质好、可利用性强等特点,在人类生产和生活及城市建设中起着不可或缺的作用。同时,地下水资源对于生态环境保护和地质亦十分重要。随着社会经济的发展,地下水可开采资源量和各行业用水不断增加之间的矛盾日益加剧。在城市建设和工农业生产中,地下水被持续不合理开发,地下水水位严重下降,会导致湿地、湖泊等自然资源的枯竭,形成地面沉降和塌陷,甚至会导致河流常年干涸、生态系统遭到破坏,影响生物多样性。哈尔滨市作为我国北方重要的工业城市,水资源需求量较大。哈尔滨市地下水年补给量为24 746.33×104m3,地下水年可开采量为22 194.83×104m3,地下水年现状开采量为23 831.00×104m3,地下水年超采比例达到了7.4%,严重影响了地下水可持续发展的能力。因此,在利用地下水资源前,需要对地下水资源的水质和水量进行评价,确保在可持续发展的基础上对地下水资源进行合理的开采和利用。

地下水水位变化是一个复杂的自然过程,地下水水位主要受到大气降水入渗、地下水侧向径流补给、地表水体入渗、地表蒸发、人工开采、向邻区侧向径流[1]等因素影响,包括地下水的补给、渗流和排泄三部分,地下水水位的预测可以在一定程度上反映地下水水位的变化规律。柳丹霞等[2]将人工神经网络模型和多元回归模型相结合,实现了堤坝的沉降预测;罗云霞等[3]将粒子群算法应用于优化调度问题,使其达到最优解,产生了更多的经济效益;曹宁等[4]利用宽度学习算法和矩阵随机近似奇异值模型建立了更为优化的SVDBL模型,弥补了地下水水位预测精度不高的缺陷,但通常情况下深度学习模型的设计非常复杂,需要进行大量计算,模型可解释性也不高;闫佰忠等[5]横向对比了基于单变量和多变量的长短期记忆(LSTM)神经网络模型,结果表明多变量长短期记忆神经网络模型能够有效地解决时序变化规律,并有效地考虑相关变量的影响,长短时记忆结构模型相较于循环神经网络模型解决了长期依赖性的问题,但需要引入更长的序列数据;管帅[6]利用广义回归神经网络基本原则,弥补了传统计算方法计算量大且假定含水层均匀规则的缺陷,但对于非相关性数据,难以很好地表达高度复杂的数据;孙强等[7]的自回归分布滞后(ARDL)模型,通过确定地下水水位变化滞后时间、影响系数和有效时段,提高了强降雨条件下滑坡地下水水位预测精度。随着人工神经网络的发展,BP神经网络凭借简单可塑的优点被广泛应用于非线性优化领域,但是存在收敛速度慢和容易陷入局部极小的缺点。因此,为了研究哈尔滨市浅层地下水埋深特征,本研究基于自适应变异粒子群算法优化的神经网络模型,具备了基本的粒子群算法和遗传算法的优点,在更好地寻找神经网络模型的阈值和权值的基础上,提高了模型的精度。

1 研究区数据来源与概况

1.1 数据来源

根据国家统计局发布的中国统计年鉴,选取2012年1月—2018年12月哈尔滨市地下水埋深和相关数据,用于地下水埋深自适应变异PSO优化神经网络模型的训练和预测。分析哈尔滨市浅层地下水分布特征是掌握地下水水情并保障地下水合理开采的重要手段。哈尔滨市从2004年始开展了地下水监测工作,历经19年,逐步形成了具有141口地下水埋深监测井(43口省级地下水观测井、98口普通级地下水观测井)全面对哈尔滨市地下水水质和水量进行监测的网络。本研究以哈尔滨市2012年至2018年地下水监测井监测数据为基础,分析哈尔滨市地下水埋深的特征,以探索哈尔滨市地下水的变化规律。

1.2 研究区概况

哈尔滨市地处中国东北平原东北部地区,黑龙江省南部,其独特的地理位置,使其成为第一条欧亚大陆桥和空中走廊的重要国际性综合交通枢纽,位于125°42′—130°10′E、44°04′—46°40′N。哈尔滨市东接牡丹江市、七台河市,北靠伊春市、佳木斯市,西与绥化市、大庆市接壤,南邻吉林省,处于东北亚的中心区域。哈尔滨市共辖9个市辖区、7个县、2个代管县级市,总面积约为53 186 km2[8]。哈尔滨市所辖县(市、区)分布情况如图1所示。

图1 哈尔滨市平面图

2 研究方法

2.1 BP神经网络的基本结构

BP神经网络模型是一种按照误差逆向传播算法训练的多层前馈神经网络,能够有效地提高数据的准确性与可靠性。BP神经网络包括输入层、隐含层、输出层三部分,每层又有若干个“神经元”节点,输入信号从输入层依次经过各个隐含层的“神经元”节点,最后至输出层,每一层“神经元”节点只影响下一层的“神经元”节点。

2.2 PSO算法优化预测模型

PSO是Eberhart和Kennedy于1995年提出的一种基于种群的随机优化技术模型。该模型是通过模仿昆虫、兽群、鸟群和鱼群等集群行为,群体中的每个成员经过学习自身和模仿他人经验来不断改变其探索模式的一种模型,一般认为粒子群体在其运动过程中受到三方面的因素影响:粒子先前的速度、粒子认知部分、粒子社会部分,即

(1)

式(1)中:v为粒子的速度,vi为第i个粒子的初始速度,c1和c2分别为设定的初始参数,rand()为0～1的独立随机数值,pbesti为第i个粒子的最优适应度位置,gbesti为全局最优适应度位置,xi为第i个粒子的初始位。式中粒子先前速度表示粒子上次的速度大小和方向;粒子认知部分指向粒子自身最好点的矢量,表示源于自己经验的部分;粒子社会部分是指粒子之间的协调合作和知识共享,粒子通过社会群体之间最好的经验决定下一步的运动。

2.3 GA算法优化预测模型

遗传算法是1975年Holland提出的一种模拟自然进化过程以寻找最优解的方法,基于生物进化论和遗传学,通过子代和父代之间的遗传保证稳定性,通过变异保证生物多样性,通过生存斗争与适者生存的原理促进进化。遗传算法在搜索进化的过程中一般不需要外部信息,仅仅用于评估个体或者解的优劣,作为以后遗传的依据。遗传算子是用于模拟生物基因的算子,包括选择、交配、突变。

2.4 自适应变异PSO优化神经网络模型

在BP神经网络的应用中,部分BP神经网络模型在训练的预测中会出现局部最小和过度拟合等状态,无法按照设定的参数进行,因此无法寻找到最优解。PSO粒子群算法是一种只需要优化函数而不需要其他辅助信息即可实现良好搜索功能的算法。自适应变异遗传算法是BP神经网络中调整神经网络权值,寻找最为合适的网络连接值和网络结构,突破BP神经网络传统的搜索方法,因此建立的自适应变异PSO优化神经网络模型如图2所示。图2中,E为粒子群算法和遗传算法优化人工BP神经网络后的输出误差,t为误差允许范围。

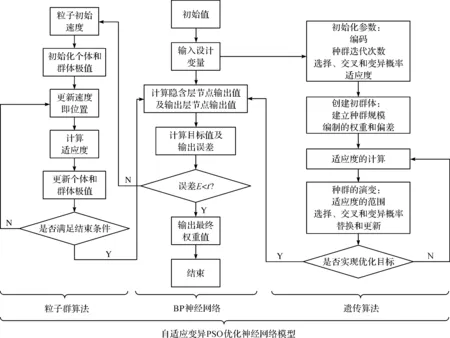
图2 自适应变异PSO优化神经网络模型

3 模型建立与结果分析

3.1 数据获取与归一化处理

根据相关文献,选取影响和表征地下水的数据作为人工神经网络模型的输入要素,包括区域降水量X1、区域蒸发量X2、区域地下水开采量(工业、农业、生活用水)X3、区域环境温度X4、区域植被覆盖率X5、区域河流对地下水补给量X6,研究区内地下水的埋深情况Y1作为输出值。

将2012年1月—2017年12月共计72组数据作为训练值,确定模型的阈值,并将2018年1月—2018年12月共计12组数据作为模型的测试集。为了消除不同评价指标之间不同的量纲,笔者对6类输入数据进行了归一化处理,使各类数据处于同一数量级,并消除了奇异数据引起的样本训练和测试误差,其计算式为

(2)

式(2)中:Xn为所输入要素的数值,Xmin为输入要素的最小值,Xmax为输入要素的最大值。

3.2 模型评价指标

笔者构建了一个双层人工神经网络BP模型,其中输入数据为6维,分别是区域降水量、区域蒸发量、区域地下水开采量、区域环境温度、区域植被覆盖率、区域河流对地下水的横线补给量,输出数据为1维,即是哈尔滨浅层地下水埋深。隐含层节点数的选择直接关系到建立的人工神经网络模型的运行性能,是导致训练时出现“局部过拟合”等情况的直接原因,因此应根据均方差MSE来确定最优的隐含层节点数。

一般最优隐含层节点个数计算式为

(3)

式(3)中:n为隐含层的节点个数,ni为输入层的节点个数,n0为输出层的节点个数,a为0～10的整数。

在机器学习中,均方差MSE经常用于评判预测模型的误差,被广泛应用于回归问题中。MSE的计算式为

(4)

式(4)中:y为实际值,yi为预测值,n为样本个数。MSE越小表示预测结果越精确,不同隐含层节点个数以及其对应的MSE如图3所示。由图3可知:当隐含层节点个数设置为3时,网络训练精确度达到最优解,因此n=3为模型隐含层节点的最佳个数。

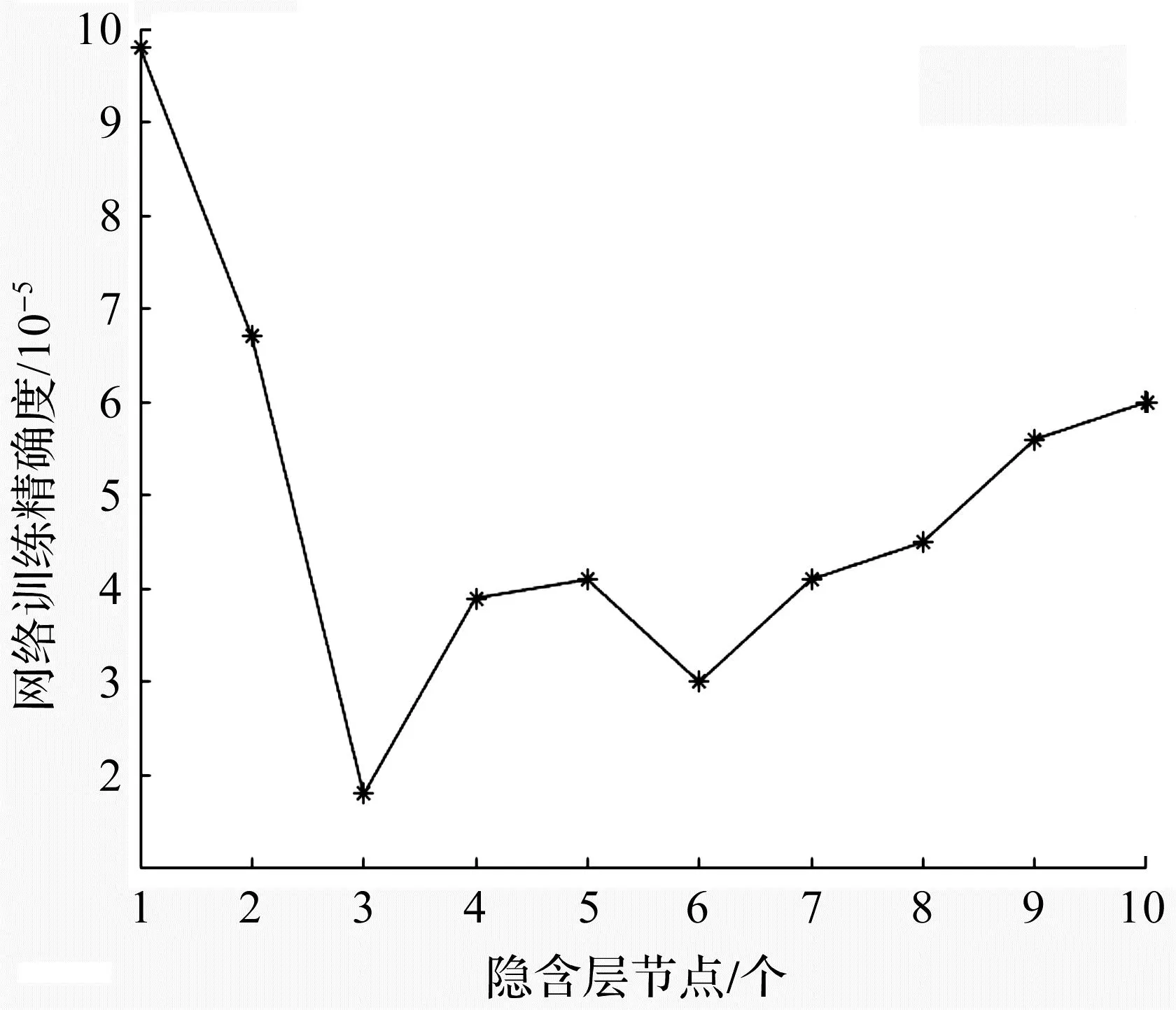
图3 自适应变异PSO优化神经网络模型

3.3 实验结果分析

GA-PSO-BP预测模型的主要参数如下:输入层节点个数为6,输出层节点个数为1,隐含层节点个数为3,遗传算法种群大小为60,终止进化次数为200次,交叉概率为0.5,变异概率为0.01,粒子群算法种群大小为20,惯性常数取随机值,加速常数为1,最大飞行速度取不超过最大速度的15%。根据以上参数建立GA-PSO-BP模型,利用本月影响和表征地下水的数据对当月哈尔滨市浅层地下水进行预测,在2012年1月—2018年12月的72组数据中取前60组数据作为训练样本,后12组数据作为测试样本,预测结果如表1所示。

表1 基于GA-PSO-BP地下水埋深预测值和地下水埋深实际值比对

适用或不适用GA-PSO优化的测试集预测结果对比如图4所示。

图4 适用或不适用GA-PSO优化的测试集预测结果对比图

由图4可知,采用GA-PSO-BP模型可以对哈尔滨浅层地下水埋深进行有效预测,预测值和真实值之间的误差较小。通过评价指标RMSE对笔者所建立BP模型、PSO-BP模型和GA-PSO-BP模型进行评价,BP预测模型的RMSE值为12.11%,PSO-BP预测模型的RMSE值为9.25%,改进GA-PSO-BP预测模型的RMSE值为8.53%。综上所述,笔者建立的自适应粒子群算法优化人工神经网络模型对哈尔滨浅层地下水预测效果较好。

4 结 语

有效地利用监测数据对浅层地下水埋深进行预测和合理规划,不仅能为人类社会发展和生存提供所需的水资源,而且也对研究区域内生物多样性、自然地理环境维持稳定具有较好的作用。笔者将粒子群算法和遗传算法相结合,提出了利用混合优化算法对人工神经网络模型进行优化,从而建立哈尔滨浅层地下水埋深预测模型,不仅可以对哈尔滨地下水资源进行较为精确的预测,而且为哈尔滨地区如何对浅层地下水进行合理开发利用提供了理论指导依据。该模型具有广阔的应用前景。下一步笔者将针对哈尔滨地区特殊的寒区气候特征,对哈尔滨浅层地下水进行模拟和预测。