油浸式变压器绕组匝间短路故障对其内部电场分布的影响分析

冯婷娜 王 涛 王碧霞 孙建明 王 明 杨 萍

（1.国网新疆电力有限公司哈密供电公司 2.国网新疆电力有限公司昌吉供电公司）

0 引言

油浸式变压器是电力系统的重要设备，其安全稳定运行对电力系统具有重要意义[1-3]。变压器绕组短路时短路电流可达到额定电流的十几倍，严重损坏变压器绝缘材料的绝缘性能，从而引起绝缘故障[4-6]。研究表明，变压器绕组匝间短路故障的发生率最高，据统计，绕组匝间短路故障约占变压器绕组故障的50%~60%[7-9]。

目前，针对油浸式电力变压器内部电场分布问题，国内外有许多学者已经进行研究。韩金华分析了一起220kV 发电厂变压器匝间短路故障的现象及原因，并采用Matlab 对变压器的故障类型进行模拟[10]。饶章权、郭志楠及刘杰等学者利用有限元法对500kV的变压器高压绕组内屏线段匝间及段间的电场进行仿真分析，得到绝缘厚度和油道尺寸对匝间和段间的影响规律[11]。变压器绝缘分为主绝缘和纵绝缘，主绝缘主要指绕组之间的绝缘，刘建军和李岩对500kV 的电力变压器的主绝缘结构的电场进行仿真计算，并得到电场强度最大的地方在高压绕组的端部内表面[12]。福州大学的庄少丰对110kV 油浸式电力变压器的电场进行仿真计算，得到无短路时变压器电场强度较强的位置分布在高低压绕组之间的油隙撑条帘处，且变压器高低压绕组的上、下两端部电场强度较大[13]。A. Sinha 和S. Kaur 建立了变压器二十三段绕组短路模型，且利用有限元法仿真分析了变压器绕组在短路故障下的电磁力且计算得到最严重短路故障下的短路电流[14]。但对于油浸式电力变压器高压绕组发生匝间短路和层间短路后的电场分布的研究较少，由于变压器绕组匝间或层间发生短路故障后，绕组匝数会发生变化，电压也会发生变化，即电场强度发生改变。因此，开展变压器绕组短路电场分布的研究对变压器的运行维护和安全使用具有重要作用。

本文以S9-M-10000/10 型号的油浸式变压器为研究对象，采用有限元软件COMSOL 仿真分析不同类型的绕组短路故障对其内部电场分布的影响，仿真结果可为解释绕组匝间短路故障对变压器内部电场的影响程度提供参考。

1 仿真模型

1.1 电场计算模型

在静电场各相同性、线性、均匀的介质中，其电位与电荷密度之间的关系都可以用泊松方程和拉普拉斯方程计算，如下所示：

式中，ρ为自由电荷体密度；ε 为相对介电常数；φ为电位标量。

求解变压器二维电场时，在坐标系中，可用边值问题来表示，主要边值问题如下所示[13]：

式中，G为整个求解域；Γ1为已知电位边界；Γ2为电压为零的边界；Γin为不同介质之间的分界线。

在变压器中的任意两个相邻的介质分界面上，均满足如下方程[15]：

式中，φ1、φ2为两种介质分界面电位；ε1和ε2为两种介质的相对介电常数；n为法向量。

1.2 变压器几何模型

1.2.1 变压器绕组无短路模型

油浸式变压器（S9-M-10000/10）的基本结构参数如表1 所示，根据表1 中变压器结构参数建立变压器二维结构模型，由于变压器结构复杂，如果完全按照变压器的实际结构参数建模具有一定的困难。因此将变压器实际模型进行合理简化，将低压线圈简化为与两根铜芯等效的单根导线；瓦楞纸及撑条帘利用同等厚度的绝缘纸来代替，考虑到变压器结构的对称性，为了提高计算速度，本文只绘制变压器中间相绕组进行仿真计算。简化后的变压器几何模型如图1、图2 所示，图中白色的区域全部为绝缘油。

图1 变压器二维结构示意图

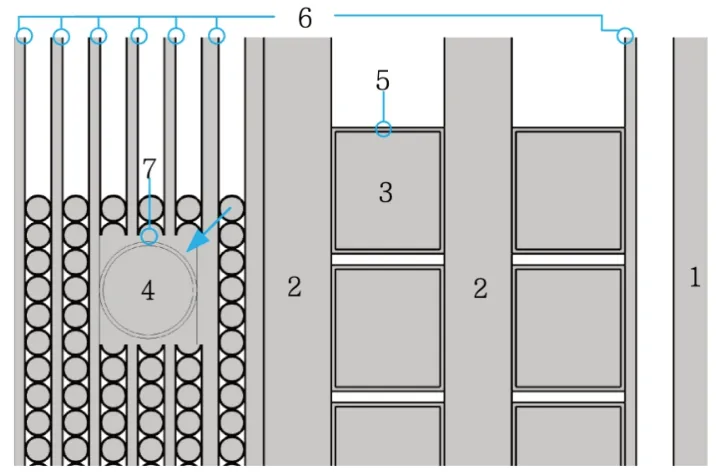
图2 变压器二维结构局部示意图

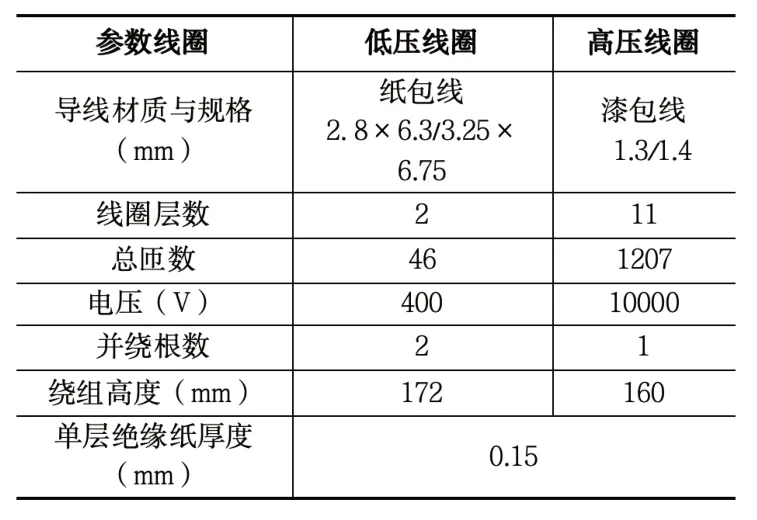
表1 变压器基本结构参数

1.2.2 变压器绕组匝间短路模型

匝间短路是指相邻的两匝线圈之间由于匝绝缘破损而造成的电路短路，因此利用分割域指令对无短路状态下的变压器模型进行分割，破坏相邻两匝绕组之间的一半绝缘层，并将两匝绕组之间的部分的材料设置为铜导体，达到匝间短路的效果，等效后的变压器匝间短路模型如图3 所示。

图3 匝间短路模型

1.3 仿真模型

本文对工频电压下的油浸式变压器内部电场进行仿真分析。在仿真过程中，高压绕组施加8165V（相电压赋值）的电压，根据S9-M-10000/10 油浸式变压器的变比1：25，绕组连接方式为Yyn 形式，因此，低压绕组施加326.6V（相电压赋值）的电压，将变压器油区域的边界位置设置为零电位。设置变压器中各部件材料的属性，绝缘油的相对介电常数为2~2.4，取2.2，绝缘纸本身的相对介电常数为6.5，油浸绝缘纸的相对介电常数为3.2~4，取3.7，各部件材料的相对介电常数如表2 所示。网格剖分时将网格的序列类型选择为物理场控制网格，网格的单元大小设置为超细化，设置完成后进行计算。

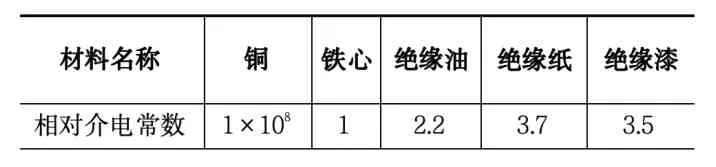
表2 材料相对介电常数

2 仿真结果分析

2.1 绕组无短路时电场分布

计算完成后得到油浸式变压器内部电场强度分布云图，由于变压器结构左右对称，因此截取变压器中间相左半边的电场强度分布云图如图4 所示，变压器绕组首端电场强度分布云图如图5 所示。

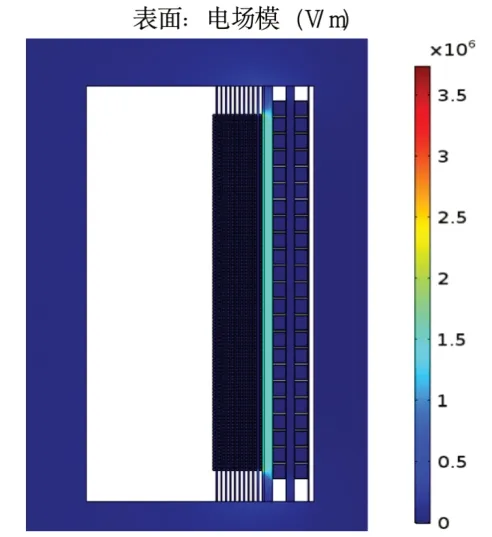
图4 变压器整体电场分布云图

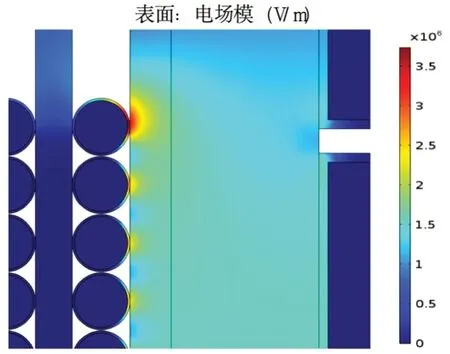
图5 变压器上端部电场分布云图

从图4 和图5 可以看出，电场强度较强的位置分布于低压绕组与高压绕组之间的油隙撑条帘处，且电场强度较大的区域主要集中在高压绕组和低压绕组的上、下两端部，最大电场强度为4.81kV/mm。这是因为油隙中电场线分布比较密集，在绕组端部周围电场分布极不均匀，且在变压器的实际结构中铁轭的不对称造成电场分布不对称[13]，使得绕组端部的等势面比较密集，端部电场强度增大。由于此变压器的油隙撑条帘宽度为8mm，通过最小击穿场强曲线可知允许击穿场强为10kV/mm，因此，变压器高压绕组首端和尾端绝缘裕度为10/4.81=2.079，绝缘裕度符合要求。

2.2 匝间短路故障对其内部电场的影响

在无短路时，变压器电场强度较强的位置分布在高压绕组端部的油隙撑条帘处，且距离油隙撑条帘位置越近电场强度越强，因此距离油隙撑条帘位置越近的位置发生故障时对电场的影响最大，同时变压器在雷电冲击电压与操作过电压作用下对绕组端部电场的影响最大[13]。因此，本文选取接近油隙撑条帘的高压绕组设置匝间短路进行仿真计算，仿真所得高压绕组匝间短路电场强度分布云图如图6 所示，在油隙撑条帘中靠近高压绕组的位置纵向绘制一条二维截线，提取二维截线上的电场强度进行对比所得曲线如图7 所示。

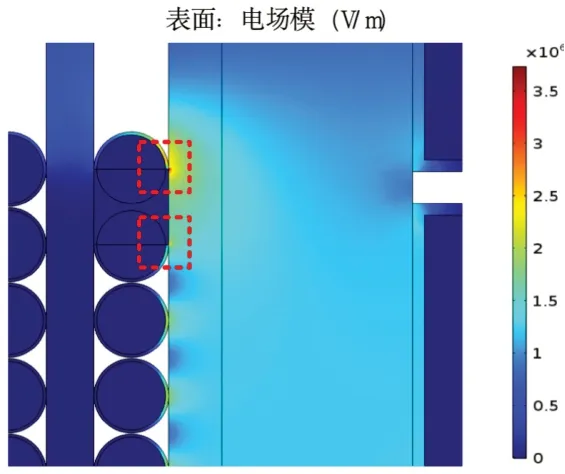
图6 匝间短路电场分布云图

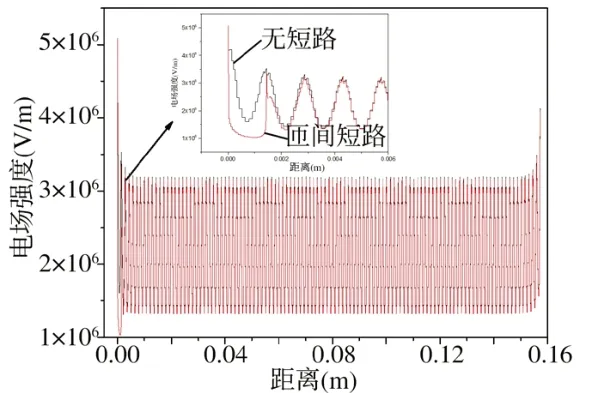
图7 匝间短路电场强度对比曲线

由图6 可知，变压器高压绕组首端两匝线圈的绝缘层被破坏后发生短路，使得首端的电场发生了变化，在两匝线圈绝缘层的切口处电场畸变最明显，最大电场强度分别为5.08kV/mm、3.68kV/mm。除短路附近位置以外，其余区域的电场基本没有发生变化，末端电场依旧为4.08kV/mm。

由图7 可知，在0~0.006m 的区域内，匝间短路位置的电场与无短路时相比发生了明显的畸变，最大电场强度从4.81kV/mm上升到5.06kV/mm，上升了5.2%；随着距离的增大，电场强度急剧下降，在0.001m 处电场强度下降至最小值，最小电场强度为1.03kV/mm；之后又开始逐渐上升，基本不受短路故障的影响，直到大于0.006m 的区域，匝间短路后与无短路时的曲线基本重合。这是因为绕组短路后，变压器绕组变比改变，而本文匝间短路位置在高压绕组上，即匝数高压侧的匝数减小，由于变压器的电压比等于其匝数比，高压侧电压随之减小，电势也随之减小，故电场强度减小。

2.3 不同短路匝数对其内部电场的影响

变压器匝间短路故障附近的电场强度与匝数有关，因此进行对比分析不同数量短路匝数对其内部电场的影响情况，根据控制变量法，在不改变短路位置的同时，建立变压器高压绕组首端不同短路匝数的短路故障模型，仿真分析不同短路匝数的故障对其内部电场的影响程度。对比曲线如图8 所示。

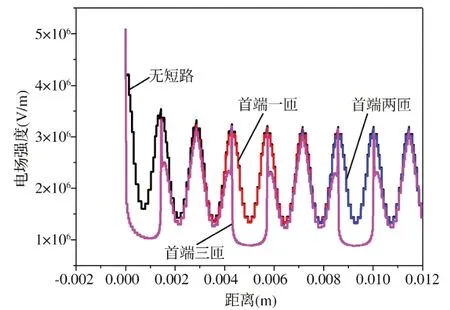
图8 不同短路匝数电场强度对比曲线

由图8 可知，变压器高压绕组首端不同短路匝数对其内部电场的影响程度不同，绕组首端线圈短路一、两匝时，对其内部电场强度的影响基本一致；而当绕组首端线圈短路三匝时，电场强度在0.011m之后才开始趋于正常。所以随高压绕组首端短路匝数的增加，局部最大电场强度增大，短路位置电场强度下降越明显，影响范围也越大。

2.4 匝间短路的位置对其内部电场的影响

变压器匝间短路的位置不同也会影响其内部电场，因此进行对比分析不同位置匝间短路故障对其内部电场的影响，根据控制变量法，在不改变短路匝数的同时，建立变压器高压绕组首端不同位置的短路故障模型，仿真分析不同位置的匝间短路故障对其内部电场的影响规律。对比曲线如图9 所示。

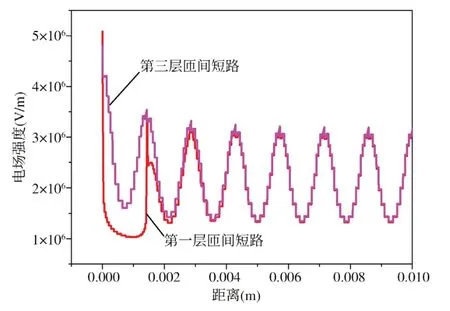
图9 不同位置匝间短路电场强度对比曲线

由图9 可知，发生匝间短路的位置不同，其对电场的影响也不相同。三种短路情况均使其内部电场发生畸变而减小，但第一层首端发生匝间短路后对其内部电场的影响较明显，第二层、第三层短路与无短路时的电场强度曲线基本重合，这是因为第一层靠近油隙撑条帘位置，而距离油隙撑条帘越近电场强度强。所以短路位置距离油隙撑条帘越近电场强度畸变越明显。因此当油隙撑条帘附近发生大面积匝间短路时，对周围电场有较大影响。

3 结束语

本文仿真分析了10kV 油浸式变压器无短路时及发生匝间短路故障时对其内部电场的影响，结论如下：

1） 变压器无短路状态运行时，高、低压绕组之间的油隙撑条帘处电场强度较强，且电场强度较大的区域主要集中在高、低压绕组的上、下两端部。

2） 变压器绕组发生匝间短路后，短路位置的电场强度呈现先减小后增大最后趋于稳定。

3） 匝间短路的数量和位置对其内部电场有较大影响，随高压绕组首端短路匝数的增加，局部最大电场强度增大，匝间短路局部电场畸变越明显，且短路位置距离油隙撑条帘越近电场强度畸变越明显。