粒子群算法在APU 转子平衡工艺中的应用

王冰 单煜峰 徐长青/中国南方航空股份有限公司沈阳维修基地

1 转子组件动平衡分析

转子组件是辅助动力装置（APU）的核心部件，转子组件的动平衡性能测试对于APU 的维修质量至关重要。APU 转子转速一般达到近50000r/min，良好的动平衡性能可以减少APU 的整机振动，降低轴承的动载荷，提高APU 的使用寿命，因此优化转子组件的平衡工艺对降低航空公司的运行成本和提高维修车间的生产效率具有重要意义。

以某型APU 转子为例，如图1 所示，其结构为弧面端齿－中心拉杆结构，组件包括前轴承轴1、负载段叶轮2、拉杆3、中间轴4、动力段叶轮5、大联轴器6、一级涡轮7、小联轴器8、二级涡轮9、后轴承轴10、模拟轴承11、垫圈12、紧轴螺帽13。

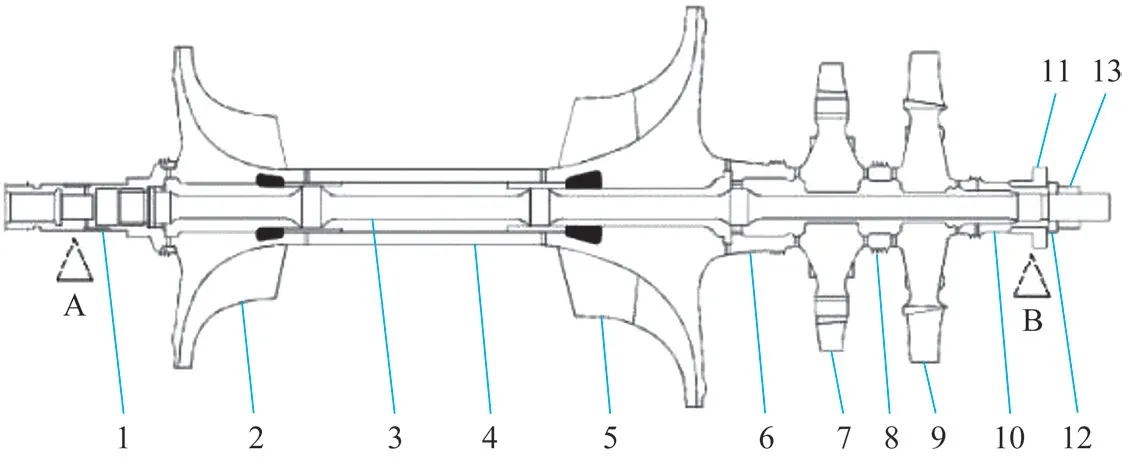
图1 APU转子结构

如图2 所示，APU 转子各部件之间通过弧面端齿结构实现啮合连接，通过拉伸拉杆以紧轴螺帽拉紧固定，以此保证端齿啮合处具有足够的刚度。因此，可采用刚体轴动平衡测量方法完成APU转子的动平衡测试工作。

依据APU 维修手册，在装配转子时需限定两个测量面（图1 中A、B）处的剩余不平衡量。当剩余不平衡量超过标准时，不能通过材料去除的方法而只能通过各部件的重新组合来减小剩余的不平衡量。由于转子本身具有足够的刚性，各部件之间连接的端齿齿数固定，且剩余不平衡量本质上为一矢量型变量，因此转子组件的剩余不平衡量可等效为各组成部分在两个测量面处的剩余不平衡量的线性组合。由于转子各部件在装配后是刚性连接并以相同转速旋转，可以将旋转坐标系作为基准坐标系，在该坐标系下进行分析，如图3所示。

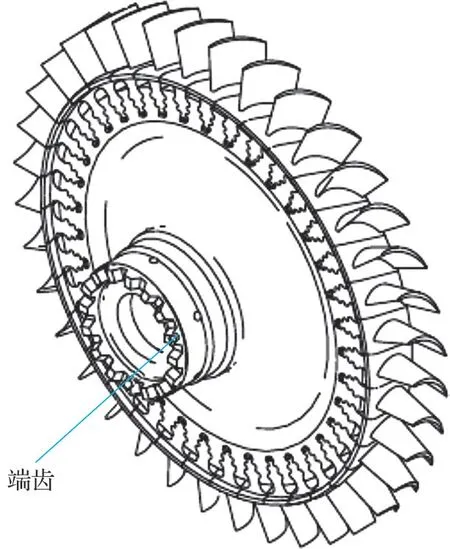
图2 涡轮端齿

图3 中坐标系X-O-Y为静止坐标系，ζ-O-η为固定在转子上的旋转坐标系，该坐标系相对于静止坐标系的旋转速度ω即为转子转速。UZA、UZB为第Z个部件在测量面A、B处的剩余动态不平衡量，UA、UB为转子组件在测量面A、B处的剩余动态不平衡量，由转子各组成部件的剩余动态不平衡量的矢量线性组合而成，即：

由于动态剩余不平衡量U包含了不平衡量的大小和方向，即U为一矢量，为了简化其表达与运算逻辑，在旋转坐标系下对矢量U在复数域进行正交分解并以复数形式表示（见图4）。

根据复数的定义，不平衡量U可表达为下式的复数形式：

根据欧拉公式，对不平衡量U可由复数形式建立复指数形式的表达方式，即：

为了得到每个部件的不平衡量UZ，可通过对该部件旋转一定角度β，分别得到两个位置时的转子组件不平衡量U与U，并按下式得到该部件的不平衡量UZ。

通过建立复数形式与复指数形式的不平衡量表达式，可以将矢量计算过程中的复杂三角函数计算简化为常规的复数加减运算及指数乘除运算，便于由计算机程序实现计算过程。

2 粒子群算法步骤

由于转子组件中的部件较多，若以全排列方法寻求最优解，则本文所用转子仅通过旋转端齿并使用全排列方法求解的计算次数将达4×1010次。目前常见的优化算法包括粒子群算法、遗传算法、蚁群算法、神经网络算法、模拟退火算法等。由于存在两个测量面，该问题又成为多目标优化问题。根据转子组件平衡问题特点，本文选择粒子群算法，该算法的优点是其路径搜索过程利于避免局部最优问题，在计算机程序上的实现也更加容易，并易于完成不同型号APU 转子的功能扩展。

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有速度和位置两个属性，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独搜寻最优解，将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

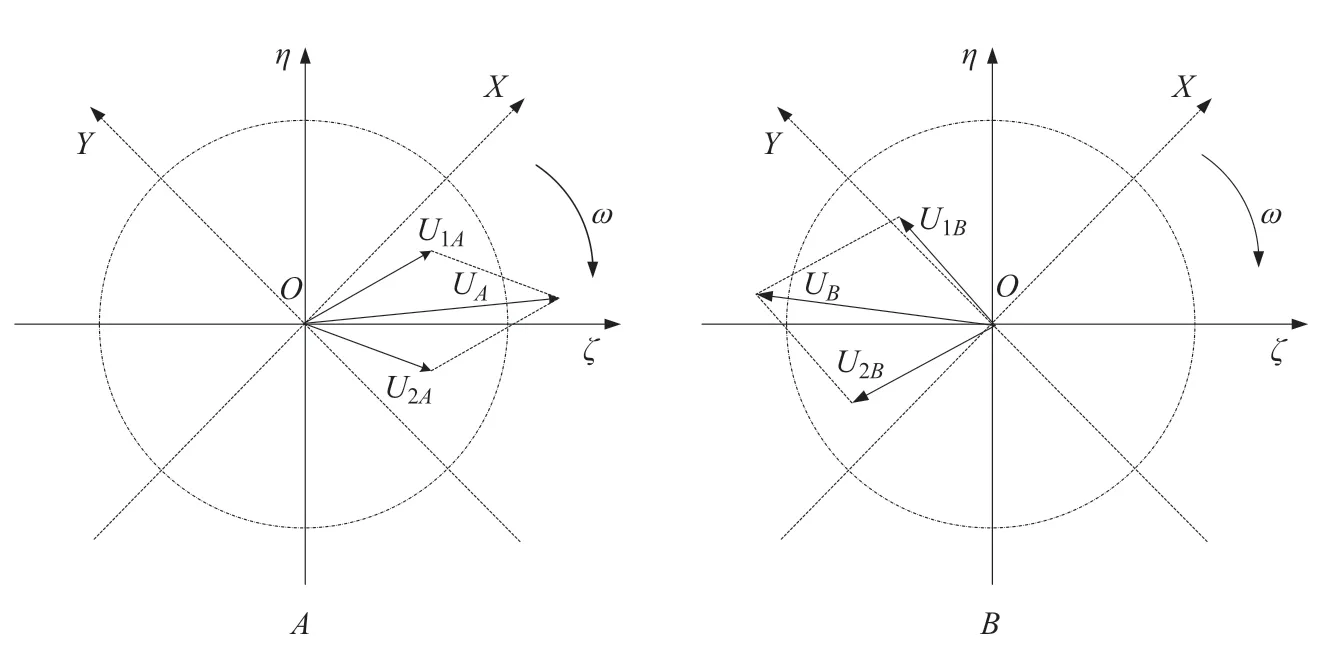
图3 矢量合成示意图

图4 矢量的复数域分解

针对转子平衡的工艺特点，将每个部件的安装角度变量所构成的集合作为待求解粒子群。粒子群算法优化步骤包括：随机初始化粒子群、计算适应度、更新粒子速度与位置、判断终止条件，计算流程如图5 所示。

1）随机初始化粒子群

依据已知参数部件的个数N，建立各部件位置变量的集合作为待求解粒子群中的一个粒子，将多个粒子组合构建成为粒子群，对各变量在取值范围内随机初始化：

2）计算适应度

适应度函数是评价粒子群中每个粒子质量优劣的标准，在本例中适应度即为剩余不平衡量的大小。由于存在两个测量面，且优化的目标之间存在耦合关系，因此取二者矢量的模求和作为适应度函数，同时对所组成的两个适应度函数加以双目标约束。

3）更新群体速度与位置

依据粒子群在寻优过程中所获得的粒子历史最佳位置Pbbeesstt与粒子群中所有粒子的历史最佳位置Gbbeesstt，设置权重系数c1、c2、c3、α及随机数r1、r2，对粒子群进行下一代更新。

4）判断终止条件

粒子群算法的终止条件以设置迭代次数为标准，当达到所设置迭代次数时程序自动终止，此时的Gbest即为算法所求解。迭代程序结束后，将所得解与约束目标进行对比，判断是否能求出所需解。

3 计算机仿真设计

依据上述理论基础，结合APU 转子平衡过程中的工艺特点，设计的程序流程如图6 所示，包括参数表达式转化、部件参数计算及组合优化计算三个模块，具体表达如下。

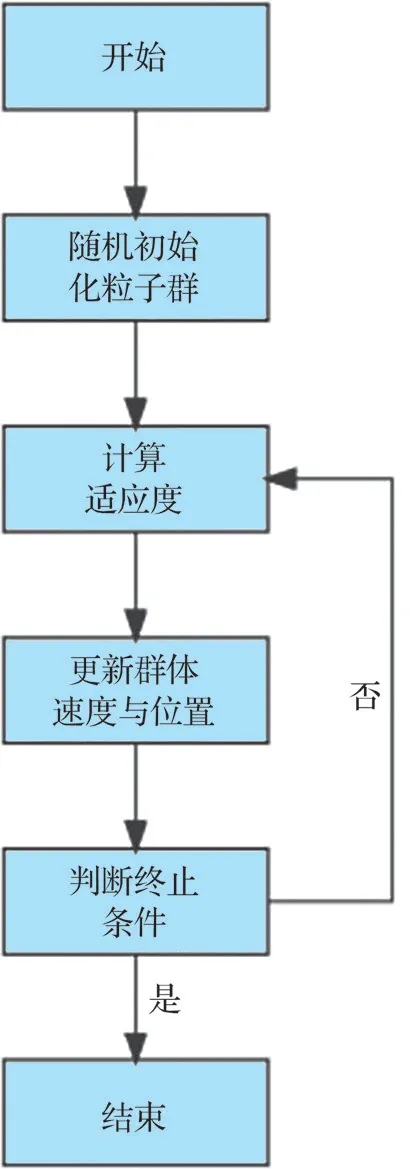
图5 粒子群算法流程图

图6 程序流程图

1）参数表达式转化：根据平衡机每次测量所得数据都为不平衡量大小|U|和所在角度θ的形式，可在输入端将其直接输入，在后台将其参数表达为复指数形式进行变量传递，并在计算过程中转化为复数形式进行计算。

2）部件参数计算：工作者在每次旋转部件前，将剩余不平衡量输入程序，旋转部件重新组合后，记录旋转的端齿数，并再次启动平衡机测量组合后的剩余不平衡量，将其输入程序，通过计算可得到该部件自身的剩余不平衡量。

3）组合优化计算：根据输入的原始不平衡量、端齿总数、A/B面限定值以及测试过程中得到的各部件动平衡参数，输入后台函数执行粒子群优化计算。

表1 测试及计算数据

表2 计算结果及验证

4 试验验证

依据维修手册，将图1 中转子组件置于图7 所示卧式平衡机上，各组成零件的端齿齿数都为20，依据维修手册要求调整支撑间距，并设置两测量面（左A、右B）剩余不平衡量限制值为35mozin 与50mozin，转速设置为1000r/min，多次测试所得数据如表1 所示。经过程序计算，最终优化方案如表2 所示。

5 结论

针对APU 转子动平衡工艺的特点及要求，提出了不平衡量的基于复数表达形式和复指数表达形式的矢量简化模型，并以欧拉公式建立二者的联系。通过粒子群法算对矢量模型的线性组合实现优化计算，编写相应的计算机应用程序，有效提高了APU 转子平衡工艺的质量与效率。