一种稻田自主播种机的路径跟踪方法的研究

梁 超 ,王洪珍 ,鲍小沾 ,张 琪

(江苏安全技术职业学院 ,江苏 徐州 221000)

0 引言

近年来,随着自动控制技术与智能化技术在农业生产中的逐渐应用[1-2],我国农业机械正在向自动化及智能化方向发展。自动导航技术是农业机械智能化的主要内容之一,自动导航系统(Automatic navigation system,ANS)可在无人驾驶的情况下使车辆按照系统预设的线路行走,还可以通过远程控制系统对车辆移动位置及周围环境进行实时监控,保证农业机械能够在规定的路径上自动工作,无需人工进行驾驶操作[3-6]。

目前,自动导航技术在汽车行业及生产中应用较为广泛,自动驾驶车辆能在各种传感器和多个系统的帮助下自行移动到指定的位置[7-8];但在农业机器人领域应用较少,研究起步较晚。由于农业生产环境较为复杂,地面不平和土壤泥泞,在非结构化环境下工作,跟踪导航误差是目前面临的关键问题之一[9-10]。

PID控制和单参数控制是农业自主导航中最常用的算法,但基于PID方法的转向控制器超调量较大、精度较低[11-13]。后期提出了一种用于自动农业拖拉机的动态路径搜索算法,以跟踪所需路径,考虑拖拉机动力学和路径跟踪误差的情况,通过在沥青和农田上的试验结果表明:横向偏差小于0.1m,直线偏差小于0.8m,但尚未考虑在农田地表泥泞环境下如何保证误差范围及提高导航精度的问题[14-17]。综上所述,基于PID或模糊的控制算法是应用于自主农业路径跟踪的最为广泛的方法,但应用于非线性系统时,PID控制器的性能较差。后期随着人工神经网络及智能算法的逐步发展,人工神经网络(ANN)逐步用于控制自动移动机器人进行路径跟踪,但人工神经网络对计算机相关技术要求较高。

笔者提出一种高精度的水稻播种机路径跟踪算法,结合侧向偏差和航向角偏差作为反馈,建立了非线性转向控制模型,对于泥泞不平的水田中直线行驶时的转向控制进行路径跟踪;为了避免倾斜引起的位置误差,考虑了车辆倾斜时侧倾角和俯仰角对位置坐标的影响;同时,详细介绍了一种考虑倾斜的可靠方法,以避免拖拉机倾斜时对路径跟踪精度的影响,实现农业机械高精度路径跟踪。

1 运动学模型的建立

笔者应用运动学模型描述了农用车辆在坐标空间中的运动,假设车辆在理想地面上以低速匀速行驶[18-19],且打滑只影响前轮,将农用车辆的运动学模型简化。在推导运动学模型时,车辆简化为自行车形状,如图1所示。方向盘所在的前轴被视为一个车轮,后轴以同样的方式被视为一个单独的车轮。该模型中使用的参数及符号如表1所示。

图1 车辆的运动学模型和参数示意图Fig.1 Kinematic model and parameters of the vehicle schematic

表1 运动学模型中的符号和参数注释Table 1 Notation of symbols and parameters in the kinematic model

如表1所示,θ的导数表示为

(1)

(2)

将式(1)与式(2)结合,θ的导数为

(3)

x的导数为

x′=vcosθ

(4)

y的导数为

y′=vsinθ

(5)

因此,农业车辆的运动学模型为[20-22]

(6)

车辆的运动状态可以定义为四阶向量[23],即

s=[x,y,θ,δ]

(7)

2 控制方法

在路径跟踪任务开始前,控制器采用位置补偿算法和转向控制算法规划行进路径。

2.1 位置补偿算法

在崎岖不平的地面上行驶时,由于GPS的传感器安装在车辆顶部,当车辆在崎岖不平的地面和投影点上倾斜时,P点在地面上的绝对坐标会受到影响,GPS传感器的影响与P不一致,故很难从全球定位系统(GPS)获取P点(见图1)的准确位置。其影响因素可分为横向位置误差,另一个为纵向位置误差。

假设GPS传感器安装高度为H,车体侧倾角为α,俯仰角为β(见图2),横向误差用elat表示,即

elat=Hsinα

(8)

纵向误差elon为

elon=Hsinβ

(9)

因此,P的坐标可用下面的方程式进行修正,即

(10)

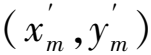
图2 倾斜引起的位置误差示意图Fig.2 Schematic diagram of position error caused by tilt

2.2 转向控制算法

与所需路径的横向偏差表示为d,可通过以下等式得出,即

(11)

其中,(xm,ym)是M的坐标;(xt,yt)是T的坐标。

假设θp是点T处路径p切线的航向角,θ是航向角,航向角偏差φ为

φ=θp-θ

(12)

转向控制算法为

(13)

其中,用于消除稳态误差的Iint是d的积分;L表示车辆轴距;v表示实现的车辆线速度;通过实验获得了转向控制参数ki和k,设置k=1.3,设置ki=0.5。

2.3 多路径控制系统

多路径控制系统主要是解决田间行驶过程中播种机直行及田间调头由于车速变化导致的算法精度下降。针对以上问题,引入路径变量signal、0、-1损失函数和变量kψ、kψd、kΔθ、kφΔ、kδ,控制结构图如图3所示。

图3 水稻播种机田间多路径控制器示意图Fig.3 Schematic diagram of multi-path controller in t he field of rice seeder

当水稻播种机处于直道时,signal≥0;在田间掉头转弯时,signal<0,变量之间等量关系为

(14)

3 试验结果与分析

试验平台为日本生产的VP6E型水稻播种机,水稻播种机的车辆轴距为1.20m,拖拉机的车辆线速度设置为0.8m/s,在转向轴上安装了一个输出6N·m扭矩的齿轮式步进电机,电机输出通过2∶1减速齿轮提供。水稻播种机配备了RTK-GPS系统,其天线位于拖拉机驾驶室顶部,用于整机运动定位。在拖拉机驾驶室上安装了一个倾斜仪,以获得俯仰角和侧倾角,用于计算位置误差;转向轴上连接了一个绝对旋转编码器,获得行进转向角,通过CAN和串行端口与所有传感器和从机进行通信。

在不均匀的稻田(100m×50m)上进行了田间试验,路径规划为平行直线,彼此之间保持5m的距离,水稻播种机的整个记录路径如图4所示,整机在试验过程中路径跟踪算法性能统计如表2所示。其转向角均方根误差不大于2.6°,每条路径的平均绝对横向偏差小于0.05m,观测到其平均绝对航向角误差小于0.5°。

表2 算法性能总结Table 2 Algorithm performance summary

续表2

由表2和图4可知:超过50%的被测点位于水稻播种机播种路径上,在理想路径的0.05m以内(见表3),水稻播种机路径3、4、5、8的横向偏差均小于0.1m(见表4),跟踪算法的性能足以满足非均匀稻田农业自动化的要求。

表4 每条路径起点处的初始横向偏差和航向角误差Table 4 Initial lateral deviation and heading angle error at the beginning of each path

所有直线路径跟踪操作期间的整个横向偏差如图5所示,数据记录如表4所示。由表4、图5可知:直线路径跟踪期间的横向偏差接近于(0±0.5)m;路径跟踪算法能够将横向偏差减小到小于0.5m以内的短距离内,路径的总体平均绝对横向偏差仅为0.028m。所有直线路径的横向偏差如图6所示。由于大多数横向偏差均小于0.5m,以试验中的路径6、7、8为例,进行横向偏差细节展示,如图7所示。

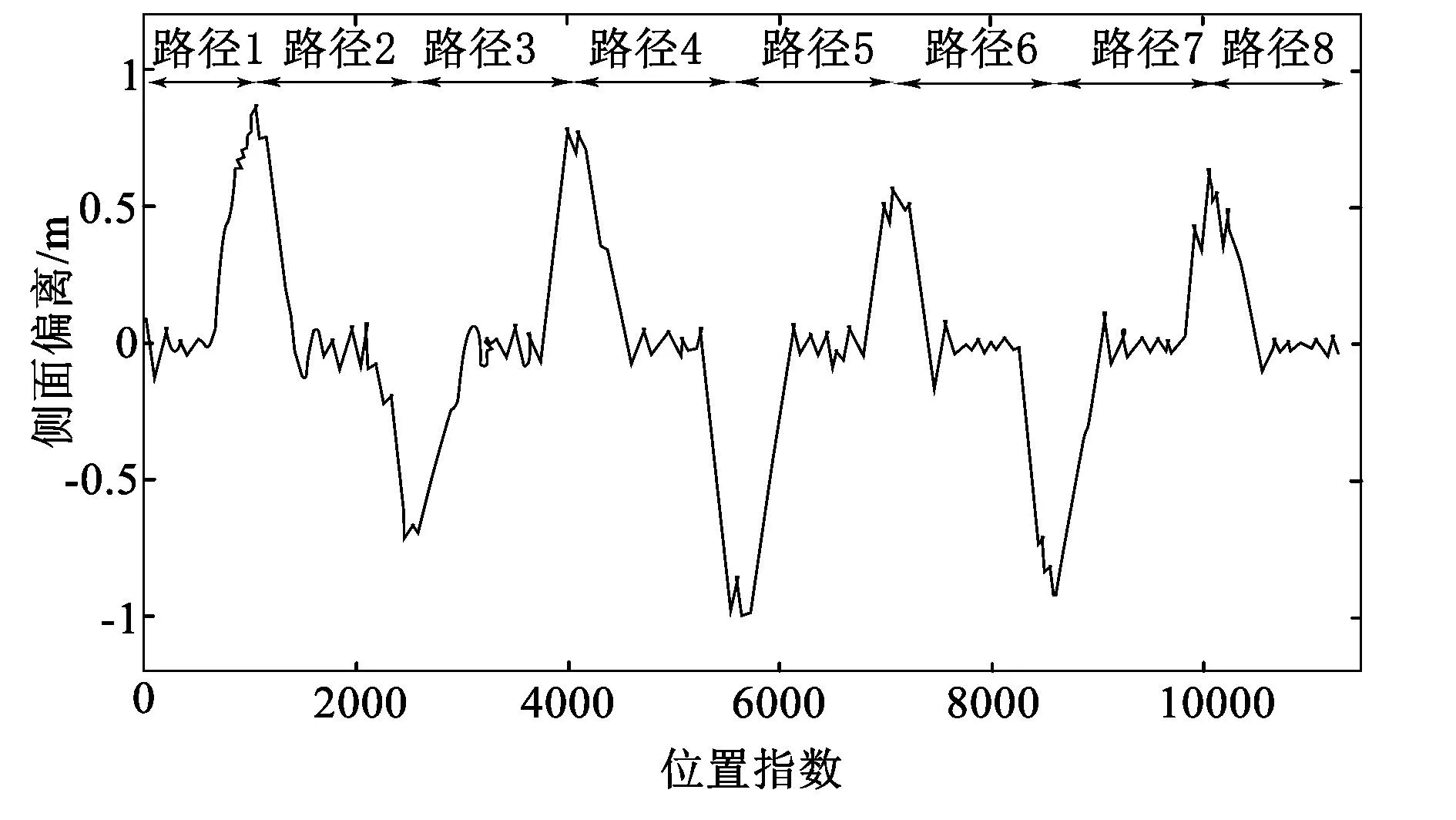
图5 试验过程中路径横向偏差Fig.5 Lateral deviation of the path during the test

图6 直线路径横向偏差Fig.6 Lateral deviation of straight path

图7 6号、7号、8号路径的横向偏差细节图Fig.7 Details of the lateral deviation of paths 6, 7 and 8

4 结论

提出了一种适用于非均匀水田水稻播种机的高精度路径跟踪算法,即补偿拖拉机位置误差算法,对水稻播种机倾斜时驾驶室倾斜对位置测量的影响进行试验研究,设计了一种带有反馈元件和积分器的转向控制模型,以高精度控制水稻播种机沿期望路径行驶。田间试验结果表明:所有测量点的平均绝对横向偏差均小于0.05m,平均绝对航向角偏差小于0.03°,速度约为0.7m/s,能够将横向偏差减小到小于0.5m以内的短距离,超过95%的测量横向偏差绝对值小于0.01m。研究结果表明:该算法的性能可以很好地应用于我国不均匀稻田的农业自动化作业,可为提高自主式水稻播种机的生产效率及水稻田间高速高精度路径跟踪的研究提供技术参考。