运动想象脑电空间滤波器选择方法研究*

王棋辉 莫禾胜 张本鑫 张绍荣*

(1 桂林电子科技大学 电子工程与自动化学院,广西 桂林 541004;2 桂林航天工业学院 电子信息与自动化学院,广西 桂林 541004)

基于运动想象脑电信号的脑机接口(brain computer interface, BCI)系统近年来在机器人控制和医疗康复等方面得到了广泛的应用[1]。然而,脑电信号存在信噪比低、随机性强和非平稳性突出等特性,导致提取稳定且具有判别性的有效特征变得非常困难[2]。

共空域模式(common spatial pattern, CSP)方法是较为常用的脑电特征提取方法。CSP方法的有效性依赖于被试特异的时间窗、频带等因素[3],因此关于这些方面的研究工作比较多。然而,空间滤波器的选择也对CSP方法的性能具有较大影响[4]。传统的CSP方法可以转化为广义特征值问题进行求解,得到特征向量和特征值后,按照特征值的大小对特征向量进行排序,最后选择最大和最小特征值所对应的特征向量来组成空间滤波器组。传统CSP方法选择空间滤波器的依据在于有效信息都是集中在极端特征值所对应的特征向量中。但是有研究工作表明,通过该方式构造的最优空间滤波器并未将最为显著有效的特征全部提取出来[5],即存在被试个体差异,无法满足所有被试显著特征的提取需求。另外,空间滤波器对数的选择也会对CSP方法的性能有所影响[6],选择过多会造成信息冗余,选择过少则会导致重要信息缺失,因此空间滤波器对数的选择也较为重要。

针对空间滤波器对数的选择问题已有一些研究工作,比如文献[6-7]。但是针对判别空间滤波器(重要空间滤波器)的选择问题,研究工作很少。目前,据我们了解只有文献[5]做了相关的工作。文献[5]提出一种基于Fisher分数(Fisher score, F-score)算法的空间滤波器选择方法,这种数据驱动的自适应空间滤波器选择方法,能够有效地避免因空间滤波器次优影响显著特征的提取。该方法的优势主要体现在自适应选择的特性上,即根据每个被试的不同情况选择出特异的最优空间滤波器,而不是人工选择统一的固定空间滤波器,有效地避免因被试差异而造成的最优空间滤波器次优问题。然而文献[5]只做了简单的尝试,后续并未做进一步的研究工作。本文基于文献[5]的数据驱动原理,分别使用三种稀疏正则化嵌入式方法和三种过滤式方法来自适应选择最优空间滤波器,系统性地研究判别空间滤波器的选择问题。

1 数据集介绍和预处理

1.1 数据说明

数据集1:文献[8]公开的运动想象脑电数据集。该数据集共有15个电极通道,14个健康被试分别执行右手和脚(R和F)两种运动想象任务。其中,训练集和测试集分别有100(前1～5个轮次的脑电数据)和60(后6～8个轮次的脑电数据)个样本数据。其他详细信息参考文献[8]。

数据集2:实验室自采集数据集。该数据集一共采集了7个健康被试分别执行左手和右手(L和R)两种运动想象任务的脑电数据。使用NuAmps 40导放大器进行头皮脑电信号采集,采样率为250 Hz。去除4个眼电电极通道和2个参考电极通道的数据,只对剩余30个电极通道的脑电数据进行数据处理和分析。数据采集的具体过程参考文献[9]。

1.2 信号预处理

所有数据使用8～30 Hz、6阶的巴特沃兹滤波器进行带通滤波。选择0.5～2.5 s的时间窗提取单试次数据。

2 方法

本文的算法框架如图1所示,将方法介绍部分划分成传统CSP方法和本文提出的CSP改进方法,然后对两种CSP方法的空间滤波器选择以及显著判别特征的提取过程分别进行详细阐述。

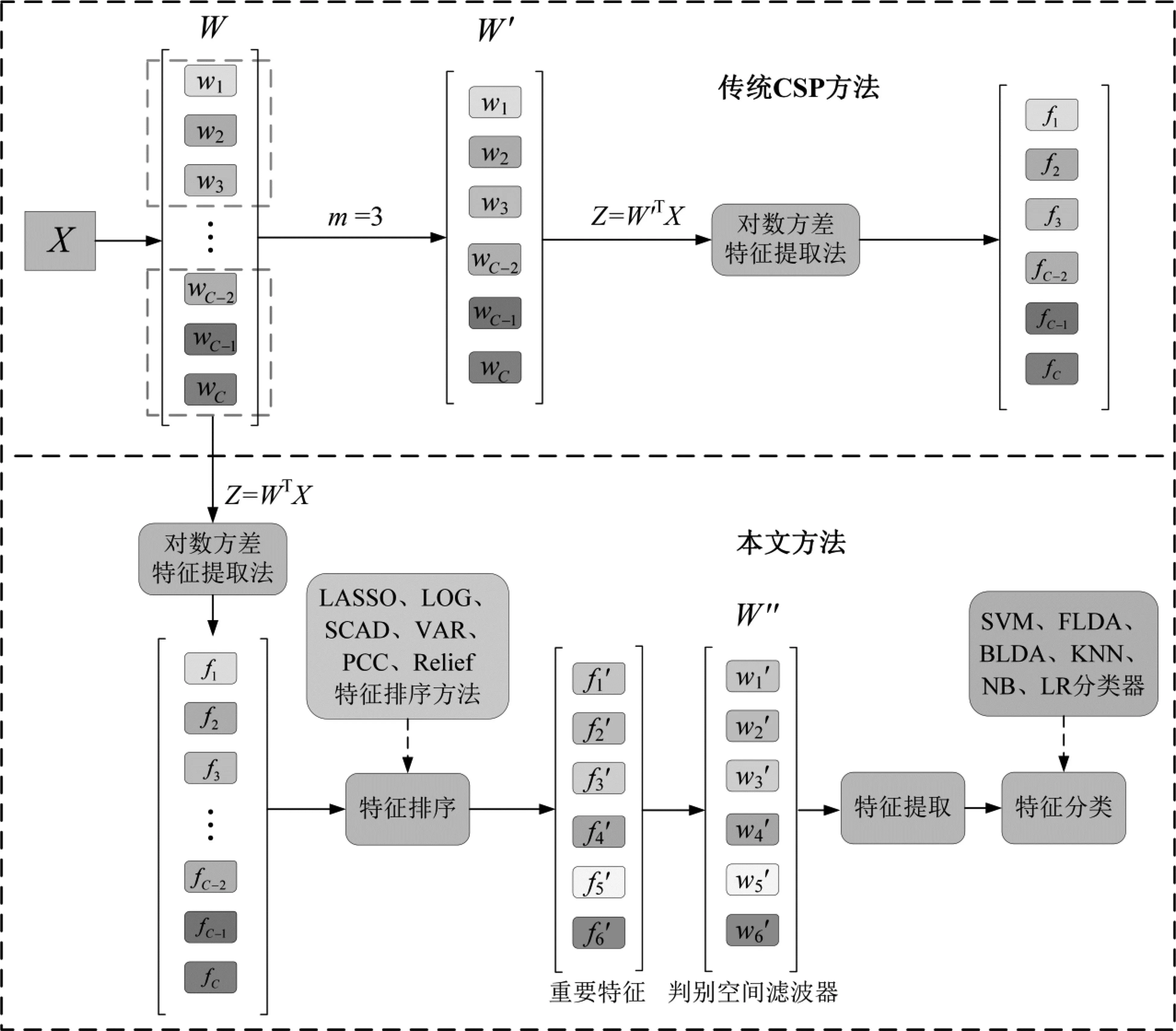
图1 本文算法框架

2.1 传统CSP方法

CSP的目标函数可转化为广义特征值问题[4],如式(1):

(1)

在传统CSP方法中,一般选择前m个和后m个空间滤波器构成最优的空间滤波器组W′,使用W′对单试次脑电数据X进行空间投影:

Z=W′TX

(2)

然后对空间滤波信号Z使用对数方差提取特征,具体如式(3):

(3)

其中log(•)为对数运算符,var(•)为方差运算符。

由图1和式(3)可看出,特征和空间滤波器具有一一对应的关系。本文选取2m个空间滤波器,在特征层面对应有2m个特征。通常m取值为3[10]。

2.2 本文方法

2.2.1 空间滤波器选择过程

由于在CSP特征提取过程中,最后的特征个数与空间滤波器个数相同且一一对应,因此本文提出基于特征选择的空间滤波器选择方法。具体地,首先提取CSP所有空间滤波器得到的特征,然后基于特征选择方法得到每个特征的权重,接着根据特征权重的大小对特征进行排序,最后进行特征及空间滤波器选择。传统CSP方法选择3对空间滤波器,即6个空间滤波器,本文也选择特征权重最大的6个特征所对应的空间滤波器构成空间滤波器组。接下来将介绍六种空间滤波器选择方法。

2.2.2 空间滤波器选择方法

如前文所述,空间滤波器选择即是特征选择。本文提出六种特征选择方法获取特征权重,分别为最小绝对值收缩和选择算子(least absolute shrinkage and selection operator, LASSO)模型、log函数(LOG)正则化模型、带平滑削边绝对偏离(smoothly clipped absolute deviation penalty, SCAD)正则模型、方差(variance, VAR)、皮尔逊相关系数(Pearson correlation coefficient, PCC)和Relief。其中,LASSO模型属于凸稀疏特征选择方法,LOG和SCAD模型属于非凸稀疏特征选择方法,VAR、PCC和Relief属于过滤式特征选择方法。

1)LASSO

假设原始特征集合为X∈RN×P,其中N为样本数,P为特征维数。y=(y1,y2,…,yN)T为样本标签,且yi∈{-1,1}。w=(w1,w2,…,wP)T为特征权重。LASSO方法的数学模型[11]如式(4):

(4)

2)LOG

LOG方法可以有效地缓解LASSO模型在特征选择过程中出现的有偏估计问题[12]。LOG方法的数学模型[11]如式(5):

(5)

其中a为比例系数,设置为0.02,λ>0为正则化参数。详细求解过程请参考文献[10]。LOG模型相比LASSO模型具有更强的稀疏性和光滑性,能够选择出更加显著的特征。

3)SCAD

SCAD方法与LOG方法都是一种近似无偏的稀疏特征选择方法,相比LASSO模型具有更强的诱发稀疏性,同时可以避免出现有偏估计和特征选择不一致问题[12],有利于选择出更加显著有效的特征。SCAD方法的数学模型[12]如式(6):

(6)

其中φλ,γ(•)为SCAD罚,wj表示第j个特征的权重,γ设置为3,λ>0表示正则化参数。

4)VAR

特征的方差大小能够反映出特征的变化情况以及包含信息的多少。因此方差越大的特征表示其包含的有效信息越多,对样本的分类预测越重要。假设原始特征集合为X=(x1,x2,…,xN)T∈RN×P,其中N为样本数,P为特征维数,xi∈RP为原始特征集合中的第i个样本。特征方差的计算公式如式(7):

(7)

5)PCC

PCC通过衡量特征与样本标签之间相关性,从而可判断出特征的重要程度[13],其取值范围为[-1,1]。相关系数的绝对值越大,代表该特征与样本标签的相关性越大,对样本分类预测越重要。假设y=(y1,y2,…,yN)T为样本标签,且yi∈{-1,1}。特征与样本标签的相关系数计算公式如下:

(8)

其中cov(•)表示协方差运算符,xj表示所有特征样本中的第j个特征,σ表示标准差。

6)Relief

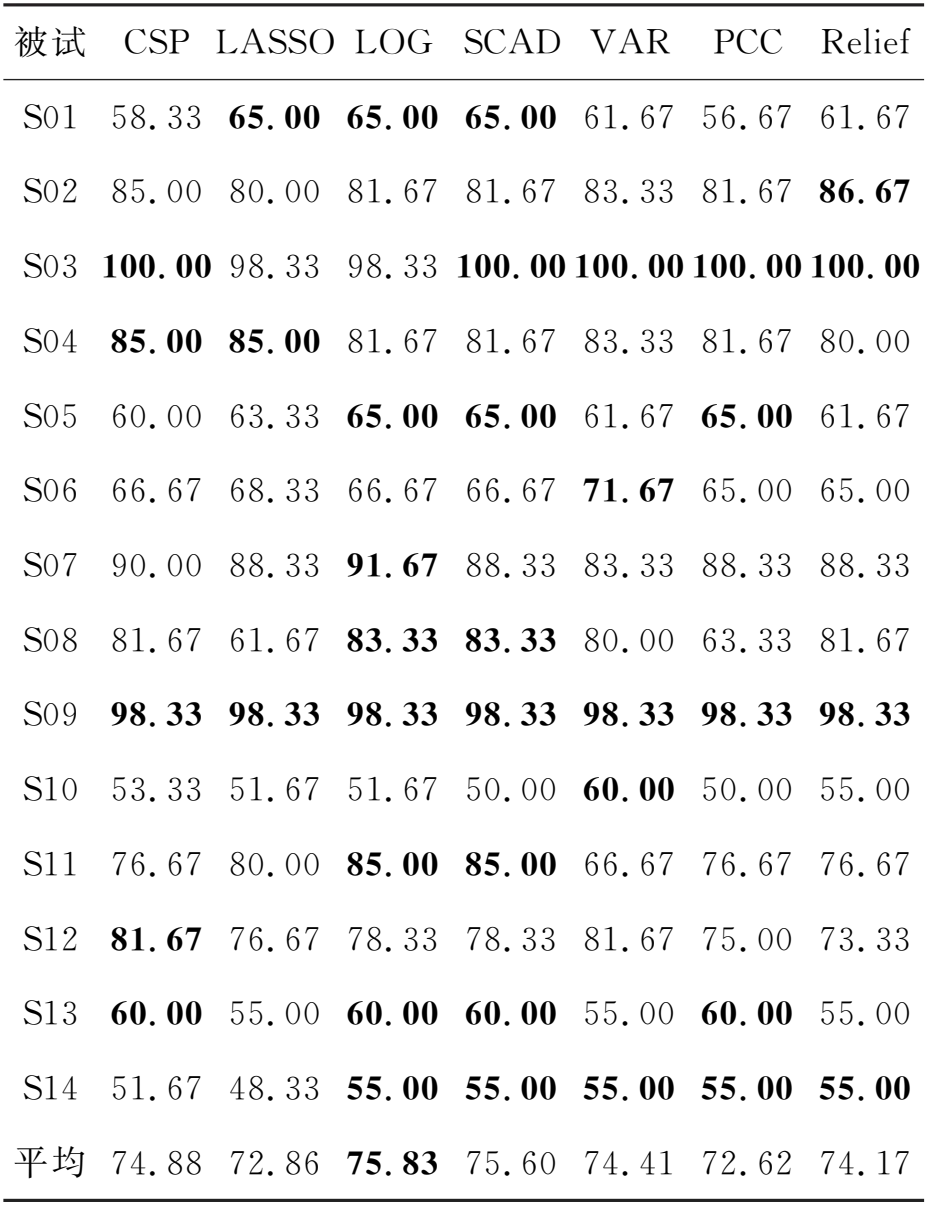
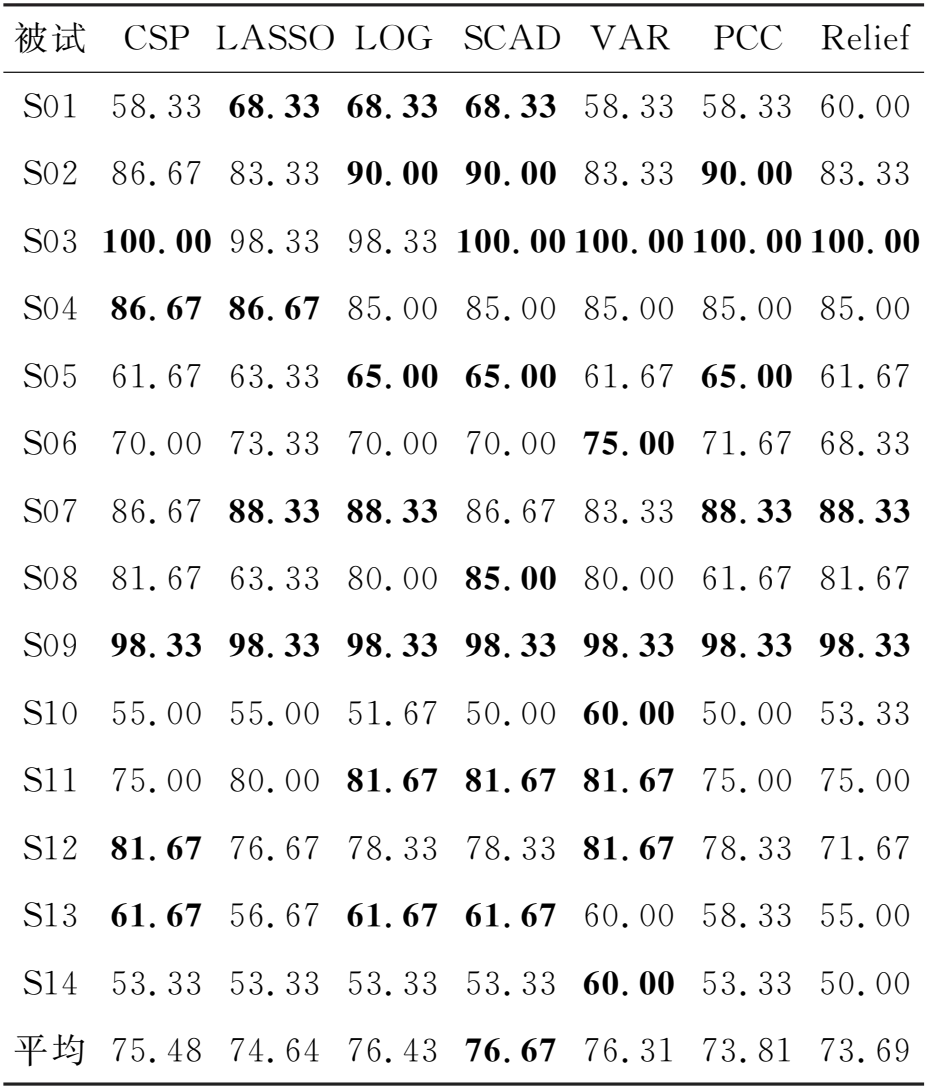
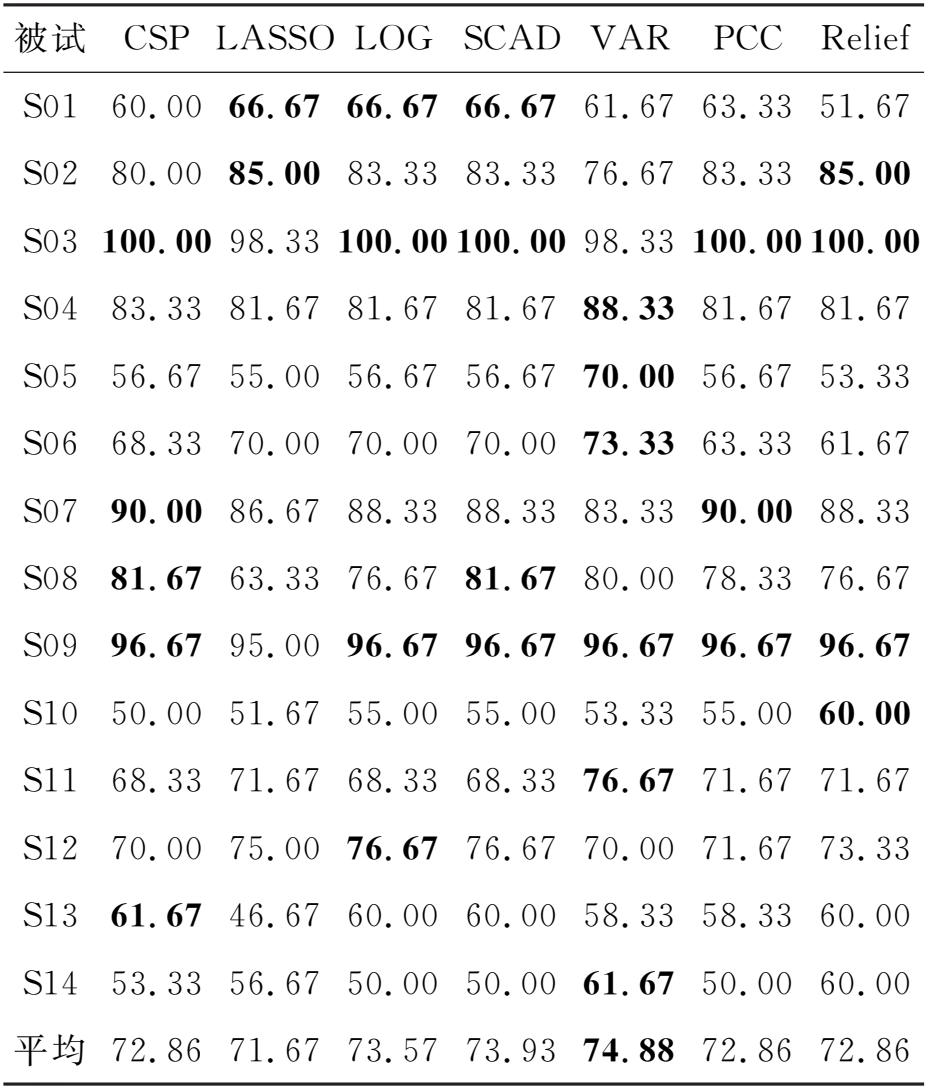
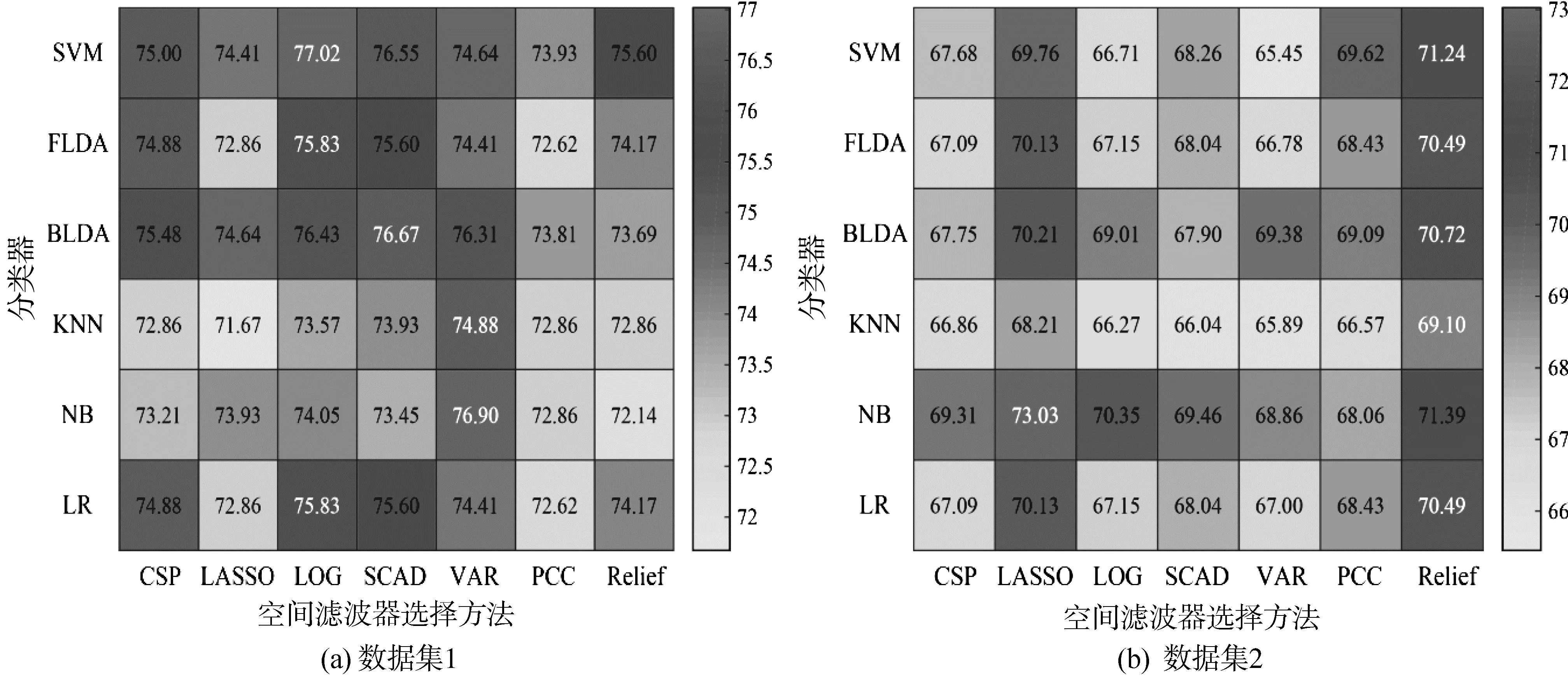
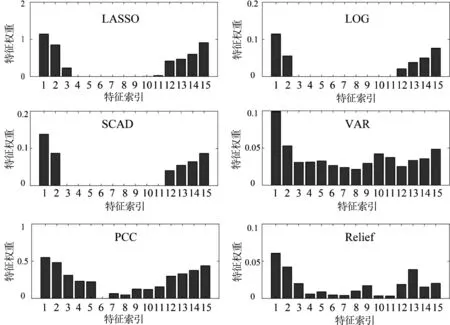
Relief算法根据每个特征和样本标签之间的相关性来赋予特征权重的大小,从而衡量特征对于分类预测的重要性。计算特征权重的过程如下:首先,从训练样本集合中选取一个样本xi;随后选择与样本xi相同类别的k最近邻样本,并且计算出两者之间的距离d1;接下来,再选取与样本xi不同类别的k最近邻样本,并且计算出两者之间的距离d2。如果d1

以上方法特征权重计算如下:对于LASSO、LOG、SCAD方法,通过10折交叉验证得到最优模型后,对模型的权重向量w取绝对值,然后按大小进行降序排序;对于VAR方法,按特征的方差大小进行降序排序;对于PCC方法,对相关系数取绝对值后按大小进行降序排序;对于Relief方法,直接按大小进行降序排序。LASSO、LOG和SCAD方法的正则化参数备选集合为:λ∈[2-5,2-4.8,…24.8,25],LASSO方法可由SLEP工具箱实现[15]。

2.2.3 特征提取和分类

根据特征权重最大的6个特征选出6个空间滤波器构成空间滤波器组W″,之后所有单试次脑电数据使用空间滤波器组W″进行空间投影滤波,最后使用对数方差方法提取特征。

使用六种分类器验证六种空间滤波器选择方法的有效性,分别为支持向量机(support vector machine, SVM)、Fisher线性判别分析(Fisher linear discriminant analysis, FLDA)、贝叶斯线性判别分析(Bayesian linear discriminant analysis, BLDA)、K最近邻(K-nearest neighbor, KNN)、朴素贝叶斯(naive Bayes, NB)和逻辑回归(logistic regression, LR)。SVM使用LIBSVM工具箱实现[16],使用线性核函数,并且模型参数采用工具箱的默认设置;FLDA和BLDA参考文献[10];KNN参考文献[17];NB参考文献[18];LR参考文献[19]。

3 实验结果

表1给出了数据集1在不同空间滤波器选择方法下,使用SVM分类器的分类结果,最高分类准确率加粗显示。从表1可以看出,LOG、SCAD和Relief方法的分类效果优于传统CSP方法,其中LOG方法最佳。

表1 分类准确率(%)(数据集1,SVM分类器)

表2给出了数据集1在不同空间滤波器选择方法下,使用FLDA分类器的分类结果。从表2可以看出,LOG和SCAD方法的分类效果优于传统CSP方法,其中LOG方法最优。

表2 分类准确率(%)(数据集1,FLDA分类器)

表3给出了数据集1在不同空间滤波器选择方法下,使用BLDA分类器的分类结果。从表3可以看出,LOG、SCAD和VAR方法的分类效果优于传统CSP方法,其中SCAD方法的分类效果最优。

表3 分类准确率(%)(数据集1,BLDA分类器)

表4给出了数据集1在不同空间滤波器选择方法下,使用KNN分类器的分类结果。从表4可以看出,LOG、SCAD和VAR方法的分类效果优于传统CSP方法,其中VAR方法的分类效果最优。另外,PCC和Relief方法的平均分类准确率与传统CSP方法相同。

表4 分类准确率(%)(数据集1,KNN分类器)

表5给出了数据集1在不同空间滤波器选择方法下,使用NB分类器的分类结果。从表5可以看出,LASSO、LOG、SCAD和VAR方法的分类效果优于传统CSP方法,其中VAR方法的分类效果最优。

表5 分类准确率(%)(数据集1,NB分类器)

表6给出了数据集1在不同空间滤波器选择方法下,使用LR分类器的分类结果。从表6可以看出,LOG和SCAD方法的分类效果优于传统CSP方法,其中LOG方法的分类效果最优。

表6 分类准确率(%)(数据集1,LR分类器)

为了进一步验证所提空间滤波器选择方法的有效性,我们继续分析数据集2的分类结果。由于空间有限,只给出了数据集2在不同空间滤波器选择方法和分类器组合下的平均分类准确率,具体如图2(b)所示。从图2(b)可以看出,在数据集2中,除了在NB分类器中LASSO方法的分类效果最优之外,Relief方法在剩余五种分类器中的分类效果均是最佳。在数据集2的分类结果中,无论使用何种分类器,LASSO和Relief空间滤波器选择方法的分类效果都优于传统CSP;在大部分分类器中,LOG和SCAD空间滤波器选择方法的分类效果优于传统CSP。其中,LASSO方法在NB分类器中取得了73.03% 的最高平均分类准确率。

另外,图2(a)也给出了数据集1在不同空间滤波器选择方法和分类器组合下的平均分类准确率。从图2(a)可以看出,在数据集1中,LOG、SCAD和VAR三种方法分别在不同分类器中取得了最佳分类效果,其中LOG方法在SVM、FLDA和LR分类器中效果最佳,SCAD方法在BLDA分类器中效果最佳,VAR方法在KNN和NB分类器中效果最佳。在数据集1的分类结果中,无论使用何种分类器,LOG和SCAD空间滤波器选择方法的分类效果都优于传统CSP。其中,LOG方法在SVM分类器中取得了77.02% 的最高平均分类准确率。

以数据集1中的被试S01为例,说明本文所提出的空间滤波器选择方法与传统CSP方法的区别,图3给出了六种不同空间滤波器选择方法得到的特征权重分布情况。如前文所述,特征的重要性对应着空间滤波器的重要性。传统CSP方法认为前3个和后3个特征的权重比较大,所以一般选择前3个和后3个特征进行分类。然而,从图3中可以看出,在六种空间滤波器选择方法中,前3个特征和后3个特征的权重并非都是最大的(或者说重要的)。比如VAR方法,第10和第11个特征的权重大于第13和第14个特征,而SCAD方法第3个特征的权重为0。在大多数情况下,新提出的空间滤波器选择方法与传统CSP方法选择的空间滤波器一致。但是本文所提的空间滤波器选择方法依据数据驱动的特征权重自适应地选择最优空间滤波器。因此,本文能够自适应地选择更加有效的、被试特异的和最具判别性的空间滤波器。

图2 数据集1和数据集2的平均分类准确率(%)

图3 被试S01的特征权重分布

本文还研究了空间滤波器选择数量对分类结果的影响。图4给出了数据集1在取不同空间滤波器对数的情况下,传统CSP方法和六种空间滤波器选择方法分别使用六种分类器的平均分类准确率。从图4可以看出,随着空间滤波器对数的增加,各种方法的平均分类准确率都是呈现先升高后降低的变化趋势。这是由于当空间滤波器的对数选择过少时,会导致重要信息不足或缺失;而空间滤波器的对数选择过多时,则会造成信息冗余,即包含噪声信息,故而空间滤波器对数选择过多或过少都会影响CSP的性能。由此可证明,空间滤波器对数的选择对CSP的性能也具有较大的影响。在不同空间滤波器对数的情况下,本文所提出的空间滤波器选择方法大部分优于传统的CSP方法,特别是空间滤波器对数为1的时候。

我们注意到文献[5]提出一种基于F-score算法的空间滤波器选择方法,与本文提出的六种自适应空间滤波器选择方法具有相同的选择原理。因此,本文将F-score方法与提出的六种空间滤波器选择方法进行对比。具体地,使用数据集1进行实验,在文献[5]的基础上,使用本文提出的六种自适应空间滤波器选择方法直接取代F-score方法。由于数据集1仅包含15个电极通道,因此本文不再进行通道选择。此外,脑电信号的频带和时间窗划分与文献[5]的设置保持一致,仍使用稀疏时-频段共空域模式进行特征提取,空间滤波器对数设置为1,利用加权朴素贝叶斯分类器(weighted naïve Bayesian classifier, WNBC)进行预测分类。

具体实验结果如表7所示,本文提出的空间滤波器选择方法优于F-score方法,其中LASSO和VAR方法的分类效果最佳。实验中发现PCC和F-score两种方法所选择的空间滤波器完全一致,导致两种方法的所有被试分类准确率都一样。出现这种情况的具体原因目前还不清楚。

图4 取不同数量空间滤波器的平均分类准确率(数据集1)

表7 分类准确率(%)(数据集1,WNBC分类器)

表8给出了传统CSP方法与本文所提方法在数据集1中的平均特征提取时间。通过对比发现,传统CSP方法的时间最短,其次是VAR、PCC和Relief三种过滤式方法,最后是LASSO、LOG、SCAD三种嵌入式方法,其中LASSO方法用时最长。本文所提方法的特征提取时间均高于传统CSP方法,其原因在于传统CSP方法是直接人工选择空间滤波器进行特征提取,而本文方法则是先提取所有特征,随即根据特征权重选择出最为重要的特征,最后基于数据驱动原理选择出与之对应的判别空间滤波器。由此可以看出,本文方法为了能够自适应选择出被试特异的最优空间滤波器,在其中加入了重要特征选择和数据驱动的过程,因此本文所提方法的特征提取时间略高于传统CSP方法。此外,由于嵌入式方法使用10折交叉验证方法来获取其最优模型,从而导致其用时高于过滤式方法。

表8 各种方法的平均特征提取时间 单位:s

4 讨论

以上实验结果比较了在不同空间滤波器选择方法和分类器组合下数据集1和数据集2的分类结果。在大多数情况下,所提出的空间滤波器选择方法的分类效果优于传统CSP方法。特别是数据集1中的LOG和SCAD方法,以及数据集2中的Relief方法。由此可以证明本文所提出的空间滤波器选择方法的有效性。另外,本文所提出的空间滤波器选择方法可以根据数据自适应地选择重要的空间滤波器。因此本文所提出的方法具有更强的适用性,可以有效提高脑电解码模型的泛化性能。

根据图2中两个数据集的平均分类准确率,我们可以看出,针对不同数据集选择合适的空间滤波器选择方法也非常重要。在数据集1中,LOG、SCAD和VAR这三种方法的分类效果较好;在数据集2中,Relief和LASSO两种方法的分类效果较好。虽然LOG、SCAD方法在数据集2中的分类效果不是最佳,但是在大多数情况下,LOG、SCAD方法优于CSP方法。因此,非凸稀疏特征选择模型具有较好鲁棒性和稳定性。

本文提出的空间滤波器选择方法可以很容易嵌入到其他方法中,以便取得更好的脑电解码性能。比如,本文的空间滤波器选择方法在时-空-频特征提取应用中取得了较好的分类效果[5]。因此,本文提出的方法不仅提升了运动想象脑电解码性能,而且具有更好的普适性。

5 总结

本文提出了六种空间滤波器选择方法,自适应地选择重要的空间滤波器,从而得到更具判别性的特征,提高运动想象脑电解码的性能。首先,基于CSP方法得到完整的空间滤波器矩阵(特征向量矩阵),接着计算所有空间滤波器对应的对数方差特征。然后,基于特征选择方法确定特征权重,由特征权重得到对应的最优空间滤波器。实验结果表明,所提出的空间滤波器选择方法优于传统CSP方法。本文方法根据数据驱动的特征权重自适应地选择重要的空间滤波器,具有更好的适应性。另外,本文方法可以很方便地嵌入到其他方法中。