小尺度圆柱涡流发生器的流动与换热特性数值研究*

吴青 王广 李林永 宁培杰 廖英可

(桂林航天工业学院 航空宇航学院,广西 桂林 541004)

20世纪70年代爆发的“两次石油危机”对全球经济和政治格局产生了深远的影响。受能源危机的影响,强化换热技术的研究得到大力的发展。强化换热技术可分为主动强化技术和被动强化技术,其中,利用涡流发生器来诱导涡旋,增加流场的扰动,强化换热效果的技术,即为被动强化技术。

涡流发生器最早应用在空气动力学领域。Johnson和Joubert[1]研究了三角翼涡流发生器对流体横掠圆柱表面的阻力和传热的影响,结果表明:雷诺数Re在5×104～4×105范围内,三角翼涡流发生器的存在会使得阻力系数减小,且发生器离驻点越近,阻力系数减小越多,同时,随着雷诺数的增加,圆柱表面的努塞尔数增加7%～17.5%。Martin和Fiebig[2]则研究了三角形和矩形涡流发生器的攻角对流动损失和换热的影响,结果显示,在大攻角的情况下,出现更加稳定的纵向涡,而流动阻力与投影面积成正比,与发生器结构及雷诺数无关,发生器附近的平均换热增强50%以上。

Park[3]利用数值模拟的方法研究间隙比对带有方形涡流发生器的通道内流动和换热的影响,选定雷诺数Re为50和150,随着间隙比从0.1增加到1,流动从稳定的非对称流动转变为对称的反向卡门涡脱落,同时,通道壁的温度分布变得更陡峭并且换热效果得到提升。Dipankar和Sengupta[4]给出了圆柱对平板近壁区流动的影响,在Re=1 200的工况下,间隙比为0.5和1.5时升力系数为0.228和0.253,对应的阻力系数为1.135和1.872,与Lei等人[5]在1999年的实验结果趋势相似。Hsieh[6]等人研究了雷诺数Re在7.8×102至1.15×104之间的范围内,平面边界附近的圆柱体周围的流动特性,当间隙比G/D<0.5时,柱后产生的交替脱落涡虽然受到壁面的抑制,但仍然能够呈现周期脱落的特性。

国内对于涡流发生器的研究主要集中在强化换热和流动控制方面。喻凡坤[7]等人列举了强化换热在工业换热设备中的应用以及流动控制减阻在动力机械中的应用,认为现有的研究都是基于模拟计算的定性分析,缺乏对实验数据的定量分析。王佳丽[8]采用大涡模拟的方法研究圆柱形涡流发生器的流动和换热情况,在流场中观察到了流场的三维特性,且通道内的换热效果得到增强,但阻力损失也随之增加,综合通道性能低于光滑通道。汪建生等人[9]研究了半椭圆式涡流发生器对流道内流动和换热的影响,认为涡流发生器诱导出的纵向涡和流向涡都能够起到强化换热的作用,且纵向涡的作用明显优于流向涡。刘春江[10]的实验和模拟结果揭示了斜截式半椭圆形涡流发生器生成的纵向涡能够强化换热,相较于同条件下的光滑通道,其平均换热系数最大可提升22.3%。汤俊洁[11]对斜截椭圆柱式涡流发生器的研究则显示斜截倾斜度也会影响换热效果。叶秋玲和周国兵[12]等人的实验研究也证明了:在低雷诺数和攻角一定的情况下,斜倾角为12°的发生器比斜倾角为20°的发生器的换热效果高10%左右。

赵云俭[13]采用大涡模拟的方法,比较了矩形通道内的小尺度圆柱及开缝圆柱对流场和换热效果,结果显示,当间隙比为4.5时,小尺度圆柱发生器的下游开始出现卡门涡街,而开缝圆柱的间隙比则为6;当间隙比为2时,两种结构的换热效果都达到最大,但是小尺度圆柱结构的Nu数较开缝圆柱的Nu数增加更多。韩志敏[14]则利用数值计算的方法模拟矩形翼涡流发生器的传热和污垢特性,结果表明:冲孔矩形翼的综合性能要优于无孔矩形翼的综合性能,且其污垢热阻相较于后者最大降低12.97%。马英华[15]通过涡流发生器对边界层流动的控制来抑制流激噪声,并能够减小涡流发生器结构本身带来的增阻影响。

然而,以前的研究多考虑发生器的形状、流体雷诺数、发生器间隙比等角度条件对发生器壁面换热和流动阻力的影响,很少有研究关注微尺度圆柱在贴近壁面区域的换热特性。此外,虽然汪健生等人[9,13]对小尺度圆柱发生器做了研究,但多限于低雷诺数下给定发生器直径参数的研究,在完全湍流区和变直径参数领域则暂未涉足,本文对这一领域进行了补充。

1 数学模型

1.1 计算模型

图1为本文计算模型示意图。参考汪健生等人[9,13]的模型,确定该计算域为矩形通道,其长×宽×高为754 mm×377 mm×120 mm;圆柱形的发生器设置在沿流向方向的377 mm处,与流体流动方向垂直且与模型下壁平行,发生器圆心距通道下壁的距离为G,该值与间隙比G/D有关。发生器直径D分别取2 mm、4 mm、6 mm、8 mm和12 mm,间隙比G/D则分别取0.5、1.5、2、3、4.5和6。结构参数及工况参数见表1。

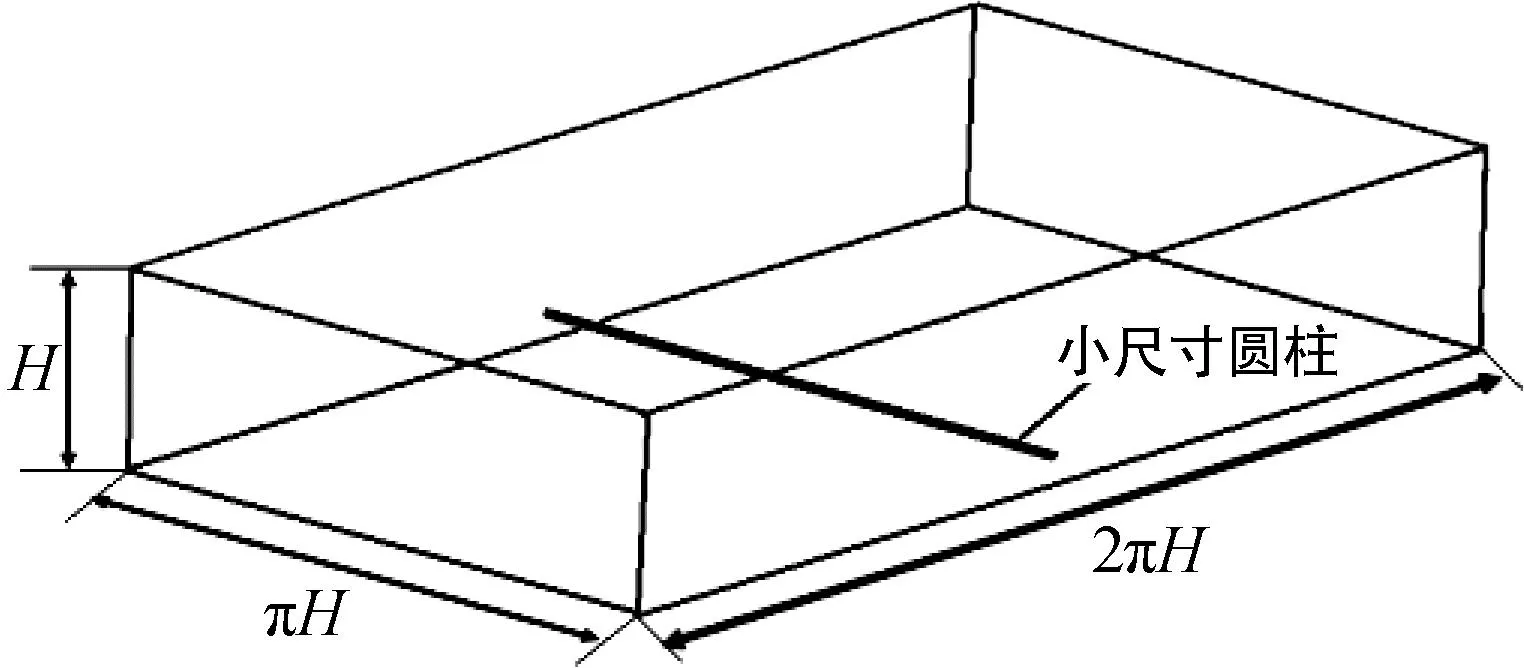
图1 计算模型

表1 涡流发生器参数表

1.2 边界条件

模拟计算中,相关边界条件设定如下:模型进口设定为流量进口,可由进口流量计算进口雷诺数,冷却空气进口温度Tin=293 K;出口设定为压力出口,出口绝对压力为1.013 25×105Pa;通道底部为恒定壁温Tw=313 K,通道上部为绝热边界,沿展向设定为周期性边界;为消除由于涡流发生器导热所产生的对流场和温度场的影响,涡流发生器的表面也设为绝热边界条件。

1.3 参数定义

定义当量直径de:

(1)

其中:Ae为过流断面,冷却空气充盈整个通道,因此Ae=πH×H;χ为湿周,因模型展向设为周期性边界,非无滑移壁面,故而湿周χ=2πH。

定义进口雷诺数Re:

(2)

其中:qm为进口流量,kg/s;υ为动力粘度,m/s2;de为当量直径,m。

为描述湍流发生器对壁面换热的影响,定义传热系数Nu:

(3)

其中:λ为导热系数,W/(m·K);h为对流传热系数,W/(m2·K)。即

(4)

定义壁面剪切应力τ:

(5)

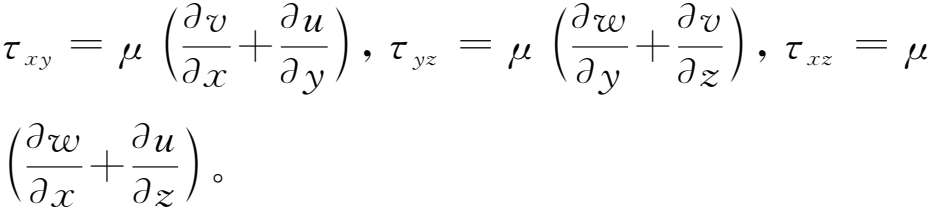
2 数值方法及结果验证

2.1 网格划分

使用ICEM软件对计算域进行分块网格划分,局部网格如图2所示。对固体近壁面进行网格加密处理,以保证z+在30左右,满足标准型壁面函数处理的要求。为验证网格无关性,选定进口Rej=29 956时的模型,计算得到该模型的网格数量在50、75、100、130、155、170及200万时通道下壁面的平均努塞尔数Nu的变化。如图3所示,随着网格数量增加,Nu趋于稳定值。综合考虑到网格数量、计算精度以及计算时间后,最终选择计算网格数量大约为130万。

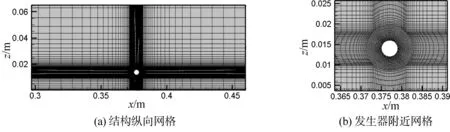
图2 网格局部示意图

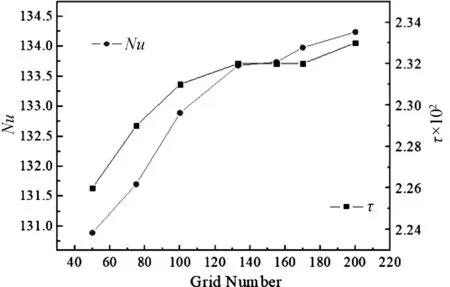
图3 网格独立性验证

2.2 数值模拟方法

本文在进行模拟计算时采用广泛应用和认可的CFD商用软件Fluent,控制方程由有限容积法进行离散。求解器采用分离隐式求解器,空间离散化梯度为基于单元的最小二乘法,各控制方程采用二阶精度进行离散,压力速度耦合方法采用SIMPLE方法,压力差值方式采用标准方式,并启用能量方程。湍流核心区选用Realizek-ε方程,近壁面处则采用标准壁面函数进行计算。计算经过Fluent软件至少迭代8 000次,最终收敛解的判断标准为监测量的残差小于1×10-3,并保证其不再有减小的趋势。

2.3 换热特性验证

为验证本文计算方法的可靠性,对未布置发生器的光滑通道进行模拟,并将计算所得的结果与相应的准则关系式进行对比,对比采用Gnielinski公式[16]如下:

(6)

其中:d为水力直径;l为槽道长度;f为管内湍流流动的Darcy阻力系数,可按科纳科夫公式进行计算:

f=(1.8lgRe-1.5)-2

(7)

实验验证范围为:Ref=2 300～106,Prf=0.6～105。

本文计算雷诺数Ref小于105,Prf取0.7,符合经验公式适用范围。将模拟计算得到的结果和通过经验公式计算的结果进行比较,如图4所示。计算时,模型尺寸相同,冷却空气入口温度为293K,给定槽道下壁壁温为313K,其他壁面绝热,壁面无滑移。

图4 计算精度验证

从对比结果上看,在雷诺数较低的情况下(Ref<60 000),模拟值与计算值的相对误差小于10%,随着雷诺数的增加,误差则增大。本文计算雷诺数范围内,计算误差在12%以下,证明本文所采用的计算方法是可靠的。

3 计算结果分析

3.1 间隙比对通道内流动和换热的影响

3.1.1 间隙比对通道内流动的影响

图5为直径D=6 mm,间隙比G/D取0.5～6时,流道内圆柱附近局部速度云图,发生器的阻碍使得柱后形成局部低速区域,从壁面分离的流体在该处形成漩涡,并在下游脱落,在主流的影响下形成上下扫动的稳定的低速带。在低速带外侧,被圆柱排挤的流体加速并与主流混合形成明显高速区域。当间隙比较小时(G/D小于2时),被柱体排挤的流体破坏了柱体下方的贴壁低速区,使得该处的对流换热得到增强。随着间隙比的增大,流道内受旋涡脱落影响的流动区域越多。壁面对脱落涡尾流的抑制作用减弱,流体上下扫动的区域变大。尾流与近壁区流体间动量交换被削弱,近壁区流动所受的影响减小,换热效果也被削弱。

3.1.2 间隙比对通道内换热的影响

图6为不同间隙比(G/D取0.5～6)时,流道下表面的对流换热系数h的云图。该云图显示,在本算例范围内,涡流发生器正下方(x=0.38 m)对应的壁面区域的对流换热系数明显高于其他区域,且间隙比越小,该区域的对流换热系数越大,在间隙比为1.5时,换热强度达到最大值。这是由于在G/D<1.5时,发生器离壁面的间隙较小,流体流动阻力较大,发生器下方通过的冷却流体量较小,近壁流体流速较低,对边界层的削弱影响不明显,故而换热系数和剪切力变化较小。而随着间隙比增大至1.5,发生器下方空间增加,能够通过的冷却流体量变大,发生器下方形成高速区,从而使得边界层内的速度梯度变大,该处的换热系数和剪切力提升。当G/D>1.5时,发生器离壁面的间隙进一步增大,发生器下方的高速区对边界层产生的影响较小,边界层能够保持一定厚度的层流结构,此时的换热系数和剪切力都低于G/D=1.5的情况。

图5 不同间隙比的流道内圆柱附近局部速度云图

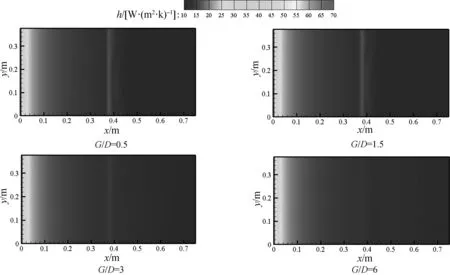
图6 不同间隙比的流道下壁对流换热系数h

在发生器的上游(0 m0.38 m),在G/D<1.5的情况下,受圆柱后脱落涡的影响,边界层受到破坏,壁面呈现局部的高对流换热区域;而当G/D>1.5,下游近壁区受脱落涡尾迹扫动的影响减小,局部的高对流换热区域消失;尤其在间隙比大于3时,除去入口段,壁面的对流换热系数基本相同。

图7则为不同间隙比(G/D取0.5～6)时,流道下表面剪切力τ的云图。与对流换热系数一样,受发生器的影响,发生器正对位置的壁面剪切力高于其他区域,发生器上游区域剪切力较小且基本不变,下游则受发生器后脱落涡的影响,出现局部剪切力较高的区域。随着间隙比的增加,发生器与壁面的距离增大,脱落涡的尾流对近壁区的影响减弱,壁面剪切力沿流向的值差减小,壁面剪切力分布较为均匀。

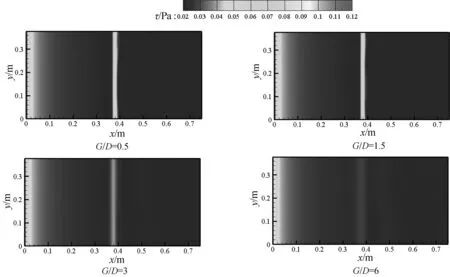
图7 不同间隙比的流道下壁剪切力t

图8和图9则为不同间隙比的流道下壁沿程平均对流换热系数h和剪切力τ。从图中可以看出,在x=0.38 m处(即发生器正对位置),不同间隙比的h和τ都取得沿程的最大值;随着间隙比从0.5增加到6,该处的h从15 W/m2×K减小至12 W/m2×K,换热系数降低20%;τ则从0.055 Pa减小至0.025 Pa,剪切力降低55%。在发生器上游,流体流过进口段后,边界层逐渐增厚,h和τ在沿程上呈现减小的趋势,h和τ分别从30 W/m2×K和0.05 Pa减小至12 W/m2×K和0.025 Pa。受脱落的尾涡的影响,发生器下游的h和τ有明显降低趋势,尤其是间隙比小于2时,h和τ减小50%左右;与间隙比为3的情况相比,间隙比取4.5和6时,高换热区域的换热系数有明显的减小,而下游区域换热效果相近。因此,综合考虑壁面总体换热强度及剪切力,间隙比G/D应取3较为适宜。

图8 不同间隙比的流道下壁沿程平均对流换热系数h

图9 不同间隙比的流道下壁沿程平均剪切力τ

3.2 发生器直径对通道内流动和换热的影响

3.2.1 发生器直径对通道内流动的影响

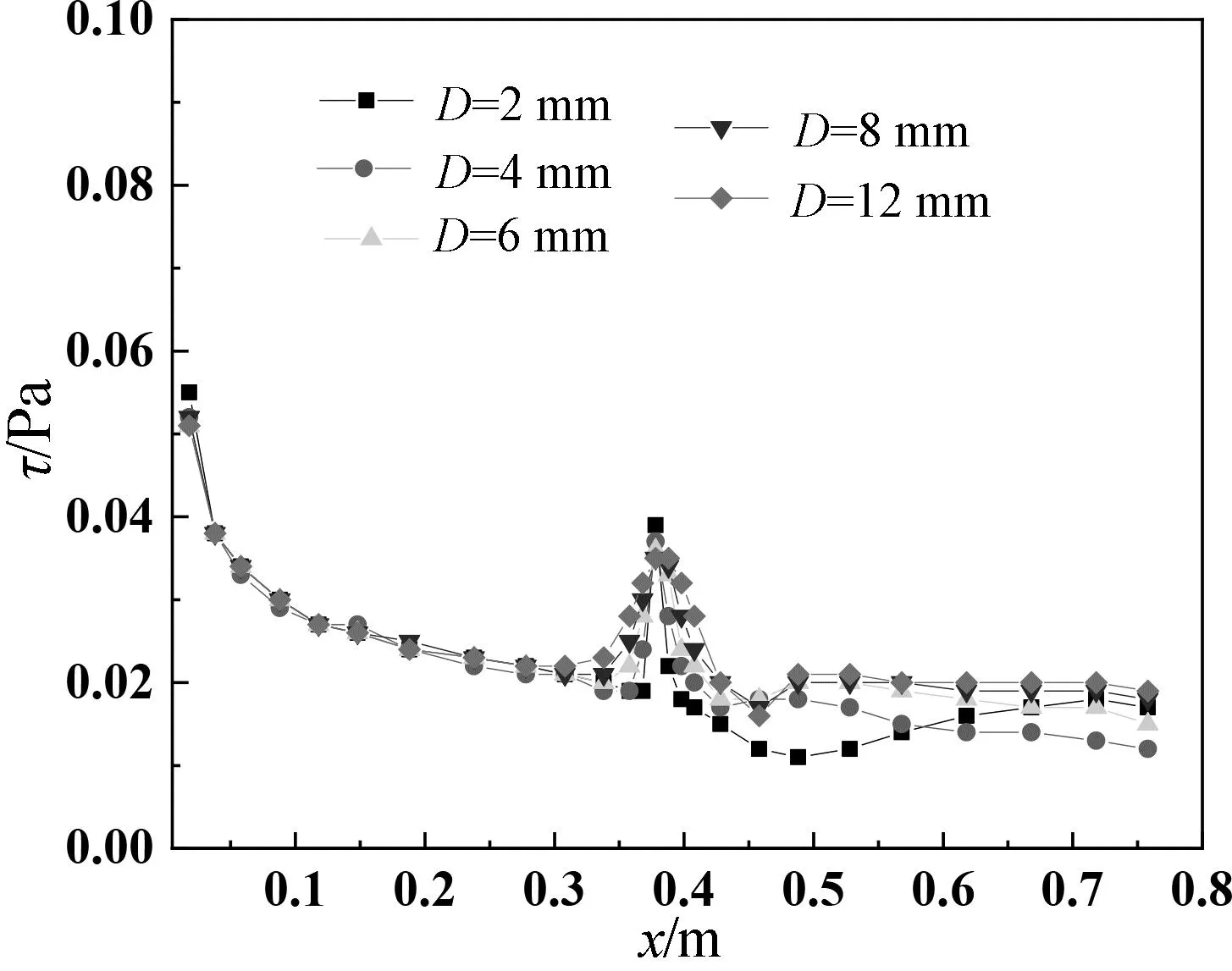
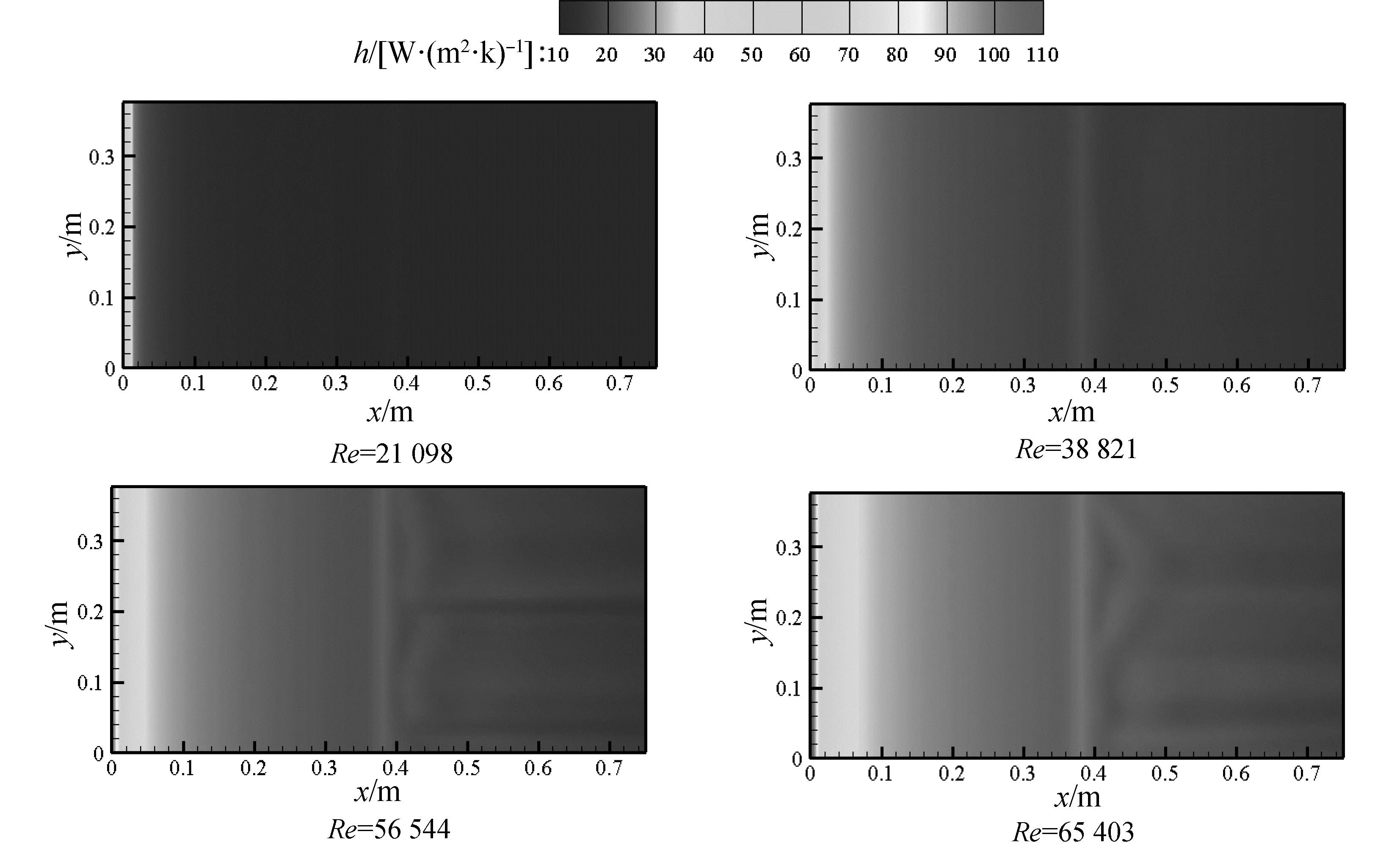
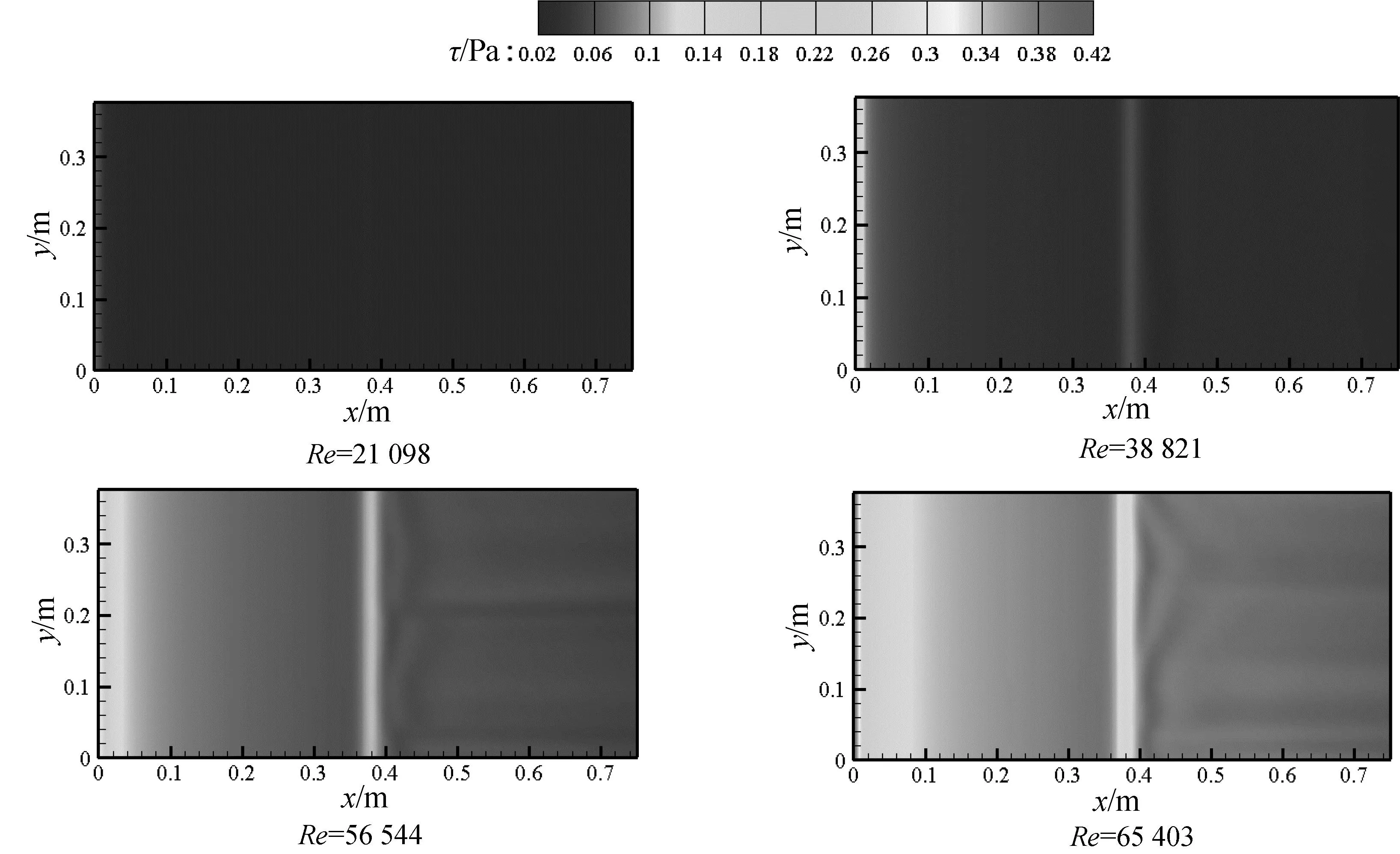
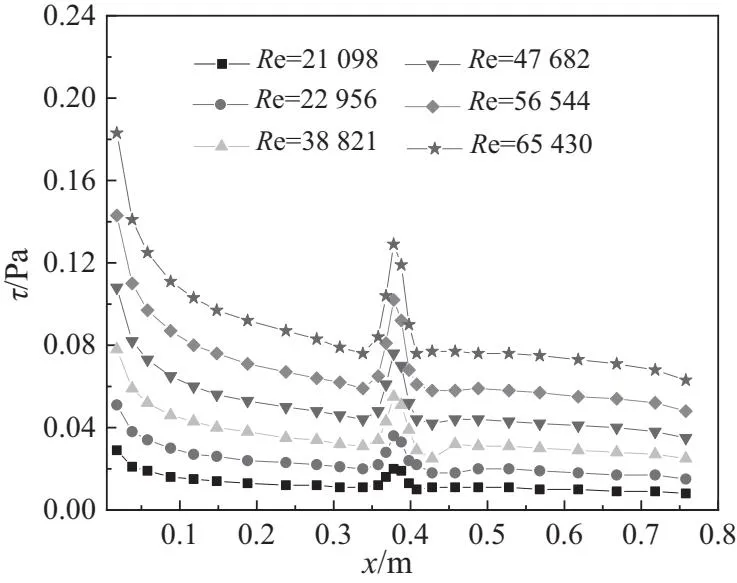
图10为间隙比为3时,不同直径下流道内圆柱附近局部速度云图。可以看出,随着直径的增加,发生器占据的流道空间增加,被排挤冷却气流量增加,受到该部分流体影响的主流区域增大。尤其当直径D大于6 mm时,在发生器附近(0.38 m

图10 间隙比为3时,不同直径下流道内圆柱附近局部速度云图

3.2.2 发生器直径对通道内换热的影响

图11为给定间隙比为3,发生器直径不同的流道下壁对流换热系数h。从图中可以看出,随着直径的增加,发生器上游区域的对流换热系数h的云图分布相似,也就是说,发生器的结构并不影响上游的流动及换热情况。发生器正下方区域(x=0.38 m处),条状的局部高换热区域的面积扩增,平均换热系数也增大,局部换热效果提升。这是由于在间隙比不变的情况下,发生器直径增大,流道的面积减小,发生器附近的流体受到排挤而加速,在发生器附近形成的高流速区域增大,则受到被排挤流体影响的近壁区域增大。

图12为给定间隙比为3,发生器直径不同的流道下壁剪切力τ。从云图中可以看出,与对流换热云图分布相似,发生器正下方区域(x=0.38 m处)形成明显的带状高剪切力区域。这说明,被发生器排挤的流体使近壁区的流体加速,增加壁面剪切力。同时,随着发生器直径的增加,受发生器排挤的流体质量增加,贴壁区受到加速流体影响增大,带状高剪切力区域的面积增加。

图11 间隙比为3时,不同直径的流道下壁对流换热系数h

图12 间隙比为3时,不同直径的流道下壁剪切力τ

图13和图14则为间隙比为3的条件下,不同直径的流道下壁沿程平均对流换热系数h和剪切力τ。从图中可以看出,不论直径取何值,从通道进口至发生器前端区域内,通道下壁面的沿h和τ都是重合的,即增加或减小发生器直径,对发生器上游壁面的流动及换热效果不存在明显的影响。在x=0.38 m处,换热系数h和τ都能达到局部最高值,14 W/m2×K和0.04 Pa;但随着直径的增加,高换热区域的范围明显扩大。在x>0.38 m的区域,当发生器直径取2时,发生器离壁面的间隙较小,发生器后部产生的脱体涡,在主流的裹挟下,与局部近壁区的流体进行掺混,损失动能,壁面换热系数和剪切力下降到5 W/m2×K和0.01 Pa。在流动发展一段距离后(x>0.55 m),脱体涡在主流的作用下逐渐消散,与近壁区流体的相互作用消失,壁面换热系数和剪切力又呈现上升的趋势,恢复到正常值。此外,可以发现,当发生器的直径小于6 mm时,该区域的h和τ从14 W/m2×K和0.04 Pa减小至6 W/m2×K和0.01 Pa,换热系数和剪切力减小50%,不利于增强换热。发生器直径大于6 mm时,发生器正对区域和下游的沿程换热系数及剪切力大致相同。因此,发生器直径宜取6 mm～8 mm。

图13 不同发生器直径的流道下壁沿程平均对流换热系数h

图14 不同发生器直径的流道下壁沿程平均剪切力τ

3.3 流动Re数对通道内流动和换热的影响

3.3.1 Re数对通道内流动的影响

图15为直径D=6 mm,间隙比为3时,不同雷诺数下流道内圆柱附近局部速度云图。随着雷诺数的增加,通道内整体流速增加,发生器上游的滞止区域减小并消失。发生器附近流体被加速的流体不断卷吸周围的低速流体,局部高速区流速增加且不断扩大,贴壁区流体流速明显增加。而在发生器的下游,脱落的漩涡卷吸周围流速较高的流体,形成上下摆动的低速带,随着雷诺数的增加,卷吸的流体流速增加,流体惯性增强,漩涡被消解,低速带受到破坏,发生器下游的低速区面积减小,下游流体流速整体增加,换热得到增强。

图15 发生器直径D=6 mm,间隙比为3时,不同雷诺数下流道内圆柱附近局部速度云图

3.3.2 Re数对通道内换热的影响

图16为给定间隙比为3,发生器直径D=6 mm时,不同雷诺数的流道下壁对流换热系数h。从图中可以看出,在不同的进口雷诺数的条件下,通道下壁对流换热系数h分布相似;但是,随着雷诺数的增加,冷却流体的质量流量增加,通道进口附近的换热得到明显的增强,且形成的高换热区域向下游扩大。此外,在发生器正下方区域(x=0.38 m处),随着雷诺数的增加,受发生器排挤而加速的流体向发生器下方流动,在黏性的作用下,近壁区流体与被加速的流体进行剧烈的动量和能量的交换,该处的高换热带的换热效果得到增强。同时,随着雷诺数的增加,发生器下方的高流速区增大,受干扰的贴壁区域增加,发生器下游出现高换热区域的扩增。

图16 发生器直径D=6 mm,间隙比为3时,不同雷诺数的下壁对流换热系数h

图17为给定间隙比为3,发生器直径D=6 mm时,不同雷诺数的流道下壁剪切力t。从图中可以看出,与对流换热云图分布相似,发生器正下方区域(x=0.38 m处)形成明显的带状高剪切力区域;同时,随着雷诺数的增加,通道进口附近的高剪切力区域扩增,平均剪切力增加。发生器正下方区域(x=0.38 m处),局部剪切力明显高于附近其他区域,形成明显的带状高剪切力区域。

图18和图19则为发生器直径D=6 mm,间隙比G/D=3,不同雷诺数为21 098～65 403时,流道下壁沿程平均对流换热系数h和剪切力τ。从图中可以看出,正如云图所显示的,在不同雷诺数条件下,h和τ的分布具有相似性,即沿程的h和τ随着流动的发展减小,同时由于发生器的干扰,在x=0.38 m处,h和τ都取得沿程的最大值。与此同时,随着雷诺数的增加,下壁面平均的h和τ整体都有所提升,进口雷诺数从21 098增加到38 821后,壁面平均的h和τ从10 W/m2×K和0.01 Pa增加到15 W/m2×K和0.04 Pa,冷却效率提升50%,剪切力提升4倍;而当雷诺数从21 098增加到65 403后,壁面平均的h和τ从10 W/m2×K和0.01 Pa增加到25 W/m2×K和0.09 Pa,冷却效率提升150%,剪切力提升9倍。因此,增大进口雷诺数虽然可以提升换热效果,但是壁面剪切力会有更大的增加,会导致通道的流动阻力升高,故而应选择合适的雷诺数。

图17 发生器直径D=6 mm,间隙比为3时,下壁剪切力τ

图18 发生器直径D=6 mm,间隙比G/D=3,不同雷诺数时,不同间隙比的下壁对流换热系数h

图19 发生器直径D=6 mm,间隙比G/D=3,不同雷诺数时,不同间隙比的下壁剪切力τ

4 结论

本文通过数值模拟的方法,对矩形通道内圆柱形湍流发生器的流动和换热特性进行计算和分析,对比了间隙比、发生器直径以及进口雷诺数对流动及换热效果的影响,并分析发生器强化换热的机理,总结出不同结构及流动参数的条件下,通道内流线及通道下壁对流换热系数h的分布规律,得出以下结论:

1)发生器的存在占据流动通道一定空间,使得流动截面积减小,冷却流体加速,在粘性作用下,贴壁区流体受到的扰动加剧,局部的换热效果有所增强。

2)在发生器直径一定的情况下,间隙比从0.5增加到6,发生器离壁面距离增加,壁面对发生器下游脱落涡的抑制作用削弱,壁面整体换热强度得到提升。然而,高换热区域与下游区域的换热系数都有所下降,故间隙比G/D应取3较为适宜。

3)给定间隙比为3,发生器直径从2 mm增加到12 mm,发生器附近被排挤的流体增加,与主流区混合后形成的高速区扩大,该处及发生器下游的贴壁区与主流区掺混加剧,换热效果明显提升。同时,发生器的直径过小(D<6 mm),换热系数和剪切力减小50%,不利于增强换热。发生器直径大于6 mm,则发生器正对区域和下游的沿程换热系数及剪切力大致相同,故发生器直径宜取6 mm-8 mm。

4)发生器结构参数不变的情况下,通道进口雷诺数从21098增大到65403,发生器正对下方区域的换热得到明显增强,而通道内流体流速整体提升,下壁面换热效果得到整体增强,但壁面剪切力也大幅提升,通道阻力随之增加。