停留时间分布理论中脉冲响应法的前置条件研究

高章帆 余子豪 游 杰

（中国成达工程有限公司）

0 引言

停留时间分布（RTD）是设备中流体流动的有效研究手段[1-2]，广泛应用于化工设备中流体流动行为的研究[3-4]以及化学反应器反混模式分析和反应速率的计算[5-6]。

脉冲响应法由于实验简单便捷，是测试设备中流体RTD最常用的方法。脉冲响应法即在t= 0 时刻在设备入口以脉冲注入方式瞬时注入示踪剂，同时在设备出口记录示踪剂的响应信号，通过该响应信号求出示踪剂的浓度响应曲线C(t)，再通过式（1）计算出设备中流体RTD密度函数E(t)[7-9]：

式中：Q——流体的流量，m3/h；

q——示踪剂的脉冲注入量，g。

采用脉响应法测定设备中流体的RTD时，理论上示踪剂在瞬间注入，但实际操作较难，注射过慢致使示踪剂注入时间不一致，可能得不到正确的RTD曲线，特别是对于流体停留时间很小的设备，快速反应器，小型换热器等，实验时应特别注意该问题，因此确定出脉冲注入时间对RTD测试结果的影响范围至关重要。

鉴于此，本文以数值模拟手段测试了不同脉冲注入时间时设备中流体的RTD，分析了其变化规律，并实验测试了设备中流体的RTD，与数值模拟结果进行对比，提出了利用脉冲响应法测试设备中流体RTD的有效脉冲时间范围，为实验提供指导。

1 研究方法与结果

1.1 理想脉冲（Ideal pulse）与实验脉冲（Actual pulse）

实验时，设备出口测得的RTD密度函数Eout(t)与设备中流体的RTD密度函数E(t)存在如下关系：

式中：Ein(t)——设备入口示踪剂的脉冲注入函数；

Cin(t) ——设备入口示踪剂的浓度变化函数。

实验时，通常假设Eout(t)等于E(t)，但实际上只有Ein(t)为理想的Dirac 脉冲函数[如式（3）所示]时，Eout(t)才完全等于E(t)，直接通过式（1）求解的E(t)会存在误差。

如图1 所示，实际的脉冲注入函数会偏离理想的Dirac 函数；实验时，只能尽量地在极短的时间内注入示踪剂。

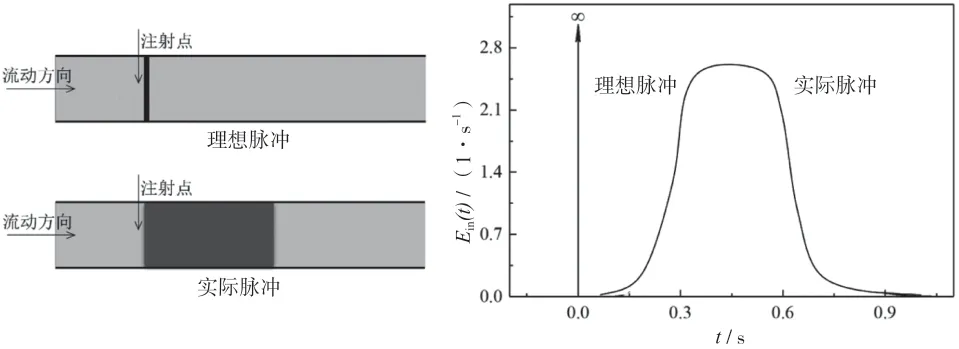
图1 入口脉冲及其RTD密度函数示意图

1.2 数值模拟方法

示踪剂的脉冲注入函数Ein(t)由其脉冲注入时间tin决定。数值模拟不受实验操作的限制，能以理想的Dirac 脉冲注入示踪剂，也能调节注入时间tin的大小。因此为探究tin对E(t)计算结果的影响，采用数值模拟方法，测试了不同tin条件下设备出口的RTD 密度函数Eout(t)，并以理想Dirac 脉冲注入下的测试结果作为对比。

本研究采用的设备模型如图2 所示，设备长为450 mm，宽和高均为150 mm，在设备中等间距布置了5 块折流板。

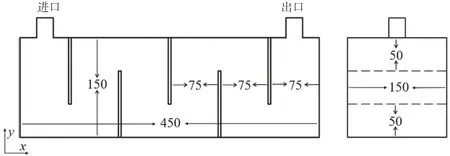
图2 实验模型（单位：mm）

根据设备几何结构的对称性，采用三维轴对称模型，将设备沿z方向的中面设置为对称面。模型结构化网格的最大尺寸为1 mm，设备的模型网格数约为514 万。

采用 Fluent 软件，在有限体积离散的计算域内建立标准的不可压缩质量守恒方程[式（5）]、Navier-Stokes 方程[式（6）]和组分输运方程[式（7）]，对壳程流体的流动过程进行三维数值模拟：

式中：t——流动时间；

f——源项；

ρ——流体密度，kg/m3；

υ——运动黏度，m2/s，

ci——单位流体中示踪剂的浓度，

Sc——施密特数；

μt——流体的湍动黏度，Pa·s。

流体介质采用常温水，流量Q为0.8 m3/h，每次RTD测试注入的示踪剂量q为3.5 g，进出口边界条件为速度入口和压力出口，出口压力设置为0 Pa，折流板及设备壁面均为无滑移壁面。选择适用范围最广泛的标准k-ε模型作为计算的湍流模型。计算方法采用压力速度耦合的SIMPLE 算法，压力插值格式采用PRESTO 算法。动量方程采用二阶迎风格式，湍动能和湍流耗散率方程采用一阶迎风格式。

模拟时测试设备出口流体RTD的步骤如下：

（1） 首先将流场计算到稳态；

（2） 在入口设置示踪剂的体积分数，并在合适的时间内注入3.5 g 示踪剂。对于理想的Dirac 脉冲，可将入口示踪剂的体积分数设置为1，并在瞬时注入3.5 g 示踪剂；同理，可在入口设置示踪剂不同的体积分数，并在不同的时间内均匀的注入总量为3.5 g的示踪剂，即可调节不同的脉冲注入时间tin，同时在设备入口监测示踪剂的浓度变化曲线Cin(t)，通过式（3）求得示踪剂的脉冲注入函数Ein(t) ；

（3） 将入口示踪剂的体积分数设置为0，并在出口监测示踪剂的浓度变化曲线C(t)；

（4） 通过式（1）求得设备出口流体的RTD密度函数Eout(t)。

1.3 模拟结果分析

定义无因次脉冲注入时间θin为：

模拟测试了脉冲时间θin在0.01～0.20 范围内5组不同θin条件下设备出口流体RTD 密度函数曲线Eout(t)的测试结果。不同脉冲时间θin条件下的脉冲注入函数曲线Ein(t)如图3 所示，与之对应的Eout(t)的测试结果如图4 所示，并与理想Dirac 脉冲的测试曲线E(t)进行对比。可以看出θin对Eout(t)曲线的形状有很大的影响，随着θin增大，Eout(t)曲线的出峰时间逐渐增大，且曲线峰值逐渐降低。

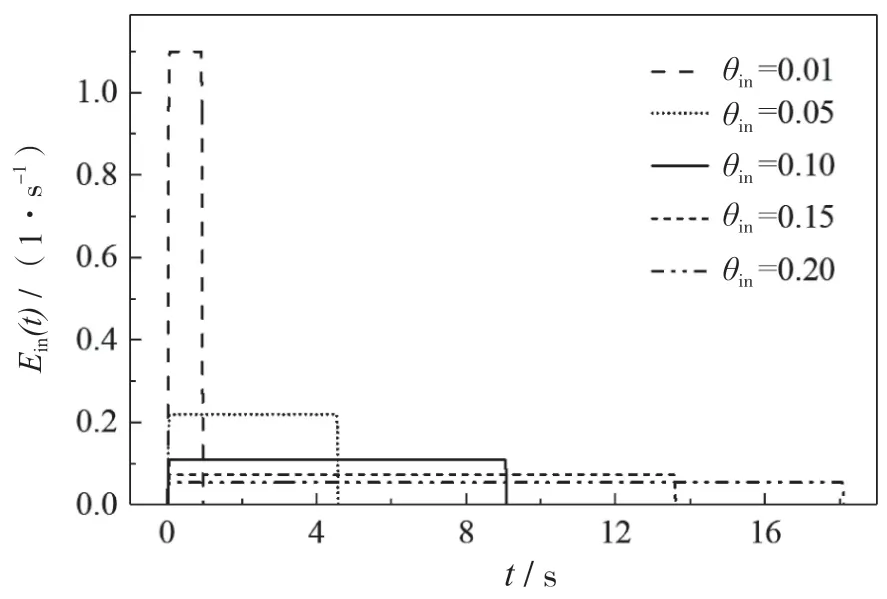
图3 不同θin条件下的Ein(t)

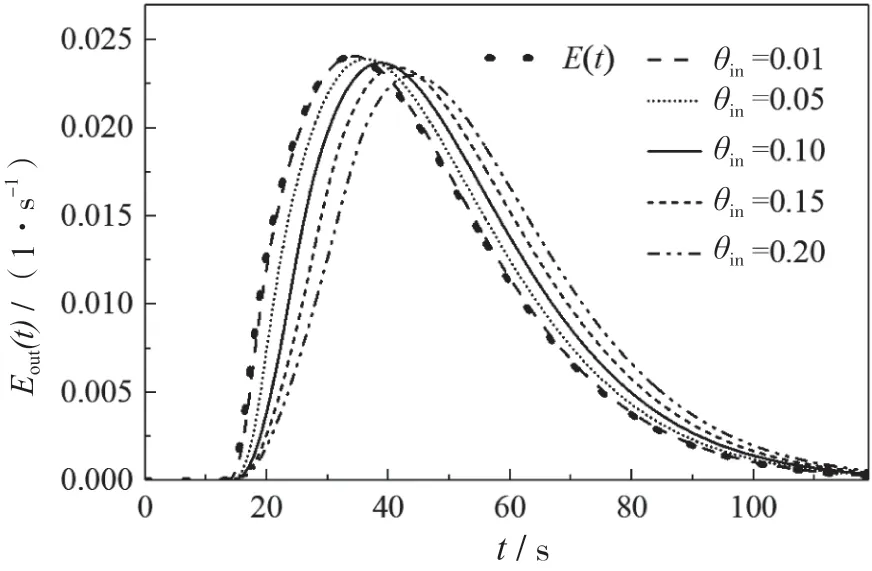
图4 不同θin条件下的Eout(t)

为了定量描述不同θin条件下Eout(t)曲线相对于理想Dirac 脉冲注入下E(t)曲线的偏离程度，将Eout(t)曲线进行数据离散，计算了Eout(t)相较于E(t)曲线的决定性系数R2：

不同θin条件下的R2如表1 所示，可以看出当θin小于0.10 时，Eout(t)相较于E(t)曲线的决定性系数大于0.9，说明此时Eout(t)与E(t)曲线有很强的相关性，且从图4 也可以看出，当θin大于0.10 以后，Eout(t)曲线与E(t)曲线有明显的偏离。因此实验时应使得示踪剂的脉冲注入时间tin越小越好，且应保证示踪剂的脉冲注入时间tin小于流体在设备中平均停留时间的1/10。

表1 θin对R2的影响

1.4 模拟方法验证

为验证模拟方法的可靠性，采用脉冲响应实验测试了模型设备中流体的RTD。

实验系统如图5 所示。实验采用氯化钾作为示踪剂，用玻璃转子流量计记录流量，当设备中流体流动稳定后用注射器以脉冲注入方式在设备入口快速注入示踪剂，本研究实验的tin在1 s 以内，相应的θin在0.022 以内，并在设备出口实时记录示踪剂的浓度响应曲线C(t)。

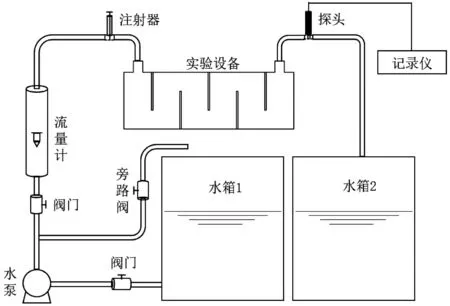
图5 实验系统

通过式（1）计算出设备出口流体的RTD密度函数曲线（Exp），如图6 所示。将数值模拟在理想Dirac 脉冲下测试的结果（Sim）与实验进行对比，可以发现模拟测得的RTD曲线与实验曲线吻合很好，说明本研究的数值模拟方法和结论是可靠的。

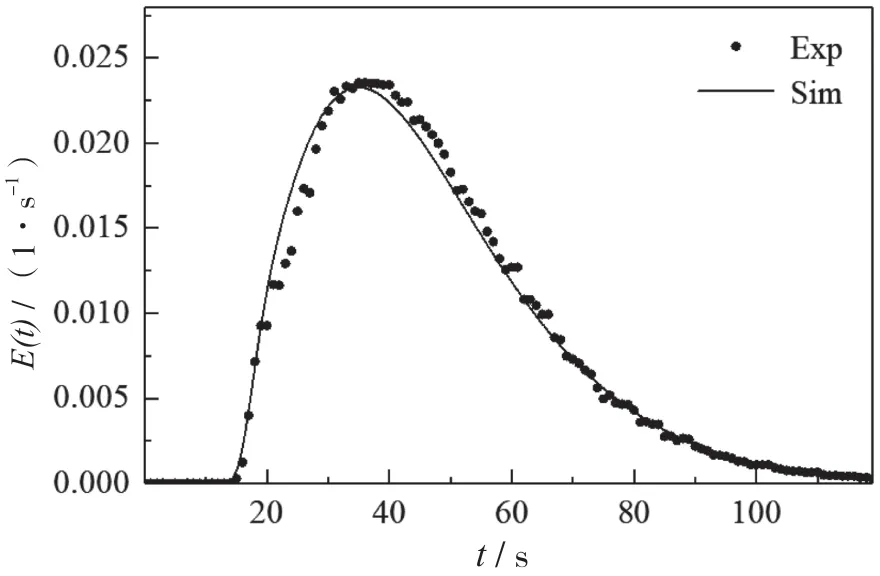
图6 实验和数值模拟结果的对比

2 结语

本研究通过数值模拟手段，采用脉冲响应法测试了设备中流体的RTD密度函数E(t)，并测试了不同脉冲时间下设备出口流体的RTD密度函数Eout(t)，将Eout(t)与E(t)进行对比发现脉冲时间对设备中流体RTD的测试结果有显著影响，脉冲时间越大，则测试的RTD密度函数Eout(t)与设备中流体实际的RTD密度函数E(t)的偏离程度越大，为了保证测得可靠的RTD结果，实验时应使得示踪剂的脉冲注入时间tin越小越好，且应保证示踪剂的脉冲注入时间tin小于流体在设备中平均停留时间的1/10。