考虑土塞效应的半埋入式管桩水平振动动力阻抗解析解答

梁志孟，崔春义，许成顺，王坤鹏，辛 宇

（1.大连海事大学土木工程系，辽宁 大连 116026；2.北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124）

引言

半埋入桩作为一种常见的基础形式，被广泛应用于桥梁、码头以及高耸建筑等各类工程结构当中。近年来，对于完全埋入式桩基水平振动的研究较为丰富，而对于半埋入式桩基水平振动特性的研究相对较少［1-4］。因此，深入开展半埋入式桩基水平振动研究，对于相关工程设计与实践具有十分重要的参考价值和指导作用。

在完全埋入式桩基水平振动研究方面，Gazetas 等［5］、El Naggar 等［6］和Mylonakis 等［7］早期将 桩侧土简化为一系列相互独立的弹簧和阻尼器，探究了完全埋入地基土中的桩基水平振动动力响应问题。进一步地，刘东甲等［8］、胡安峰等［9-10］和雷文军等［11］将桩身 简化为Bernoulli-Euler梁和Timoshenko 梁模型，分别推导出了均质和层状土中的桩基水平振动解析解答。王珏等［12-13］和梁发云等［14］则通过采用双参数（Pasternak）地基模型综合考虑了土体剪切效应对桩体水平振动的影响。在此基础上，Gazetas 等［15］、刘林超 等［16］、高洪波 等［17］和韩红霞等［18］采用Novak 平面应变理论，对不同地基条件下各类桩基的水平振动特性规律进行了探讨。此外，Haldar 等［19］、Kaynia 等［20］、干钢等［21］和刘林 超等［22］借助积分变换法和传递矩阵法，求解出了单桩水平振动解析解答。特别地，文献［23-24］和沈纪苹等［25］考虑桩芯土的作用，利用桩-土完全耦合条件推导出了管桩桩顶动力阻抗解析表达式。

在半埋入式桩基水平振动研究方面，任青等［26］基于Winkler地基模型，建立了水平、竖向荷载联合作用下的半埋入实体单桩的水平振动分析模型。在此基础上，闫启方等［27］基于Novak 薄层法，利用分数导数黏弹性模型描述桩侧土体的应力-应变关系，并借助传递矩阵法求解出了半埋入端承桩水平振动闭合式解析解答。进一步地，刘圆圆等［28］和杨紫健等［29］分别考虑地基土体纵向成层特性和饱和介质性，各自推导出了半埋入式实体桩水平振动对应解析解答。

上述半埋入式桩基水平振动的研究大多围绕单层地基和实体桩工况展开。不难看出，随着管桩在实际工程中的广泛应用，进一步开展半埋入式管桩水平振动的相关研究十分必要［30-31］。基于此，本文将基于Novak 平面应变理论，综合考虑半埋入式管桩土塞效应的影响，建立层状土中半埋入式管桩水平振动分析模型，通过引入势函数法、分离变量法以及传递矩阵法，推导出层状黏弹性土中半埋入式管桩桩顶水平阻抗解析解答。在此基础上，通过参数化分析探讨管桩埋入比、各层土体弹性模量和土塞长度对半埋入式管桩桩顶水平阻抗的影响规律。

1 定解问题力学模型的建立

1.1 力学模型及基本假设

本文所建立的层状土中半埋入式管桩水平振动力学模型如图1 所示。其中，半埋入式管桩桩顶受水平简谐荷载F0eiωt作用，F0为激振力幅值，i为虚数单位，管桩桩长为L，第i层段管桩的内径和外径分别为和，li为桩-土系统第i层段厚度。对于桩身埋入段的土塞部分（即Lp段桩身），同时具有桩侧土、桩芯土塞对管桩的横向作用力，分别为和。不同地，对于埋入段空心部分（即Lh段桩身），仅有桩侧土对管桩的作用（即为零）；而对于未埋入段外露桩身部分（即Le段桩身），由于没有地基土的约束，和均为零。基本假定如下：

（1）半埋入式管桩等效为Bernoulli-Euler 梁，忽略桩体剪切变形，桩端采用固定支承。

（2）桩侧和桩芯各层土体均为均质、各向同性黏弹性介质。

（3）桩-土系统振动为小变形，忽略土体的竖向位移。桩-土界面完全接触，无脱开和滑移现象［23］。

1.2 定解问题描述

基于Novak 平面应变理论，第i层段桩侧土体的控制方程可表示为：

类似地，第i层桩芯土塞部分的控制方程可表示为：

半埋入式管桩第i层段桩身水平振动的控制方程可表示为：

1.3 桩-土系统边界条件

（Ⅰ）桩侧土

桩-土完全接触条件：

对于无限远处，位移为零，则有：

（Ⅱ）桩芯土塞部分

当r0→0 时，有：

桩-土塞部分完全接触条件：

（Ⅲ）管桩

桩顶边界条件：

桩底边界条件：

据黎永兰的生前好友透露，黎永兰和林雪川2012年认识之后，林雪川提出交往，但黎一直以阅历、层次相差太大等为由拒绝。直到2013年，林雪川以“无耻的非法手段”逼迫黎永兰和他确认了恋爱关系。

2 定解问题求解

2.1 桩侧土振动方程的求解

对第i层段桩侧土体引入势函数，有：

式中φi和ψi表示第i层段桩侧土体的位移势函数。

将势函数式（14）代入式（1）和（2）中，可得：

式中K1(·)为一阶第二类变形Bessel 函数；Ai和Bi为待定系数。

进一步地，求解得到第i层段桩侧土体的径向和环向位移分别为：

式中K0(·)为零阶第二类变形Bessel 函数。

将式（19）和（20）代入式（6）中，可得：

2.2 桩芯土塞部分振动方程的求解

同理，对第i层段管桩桩芯土塞引入势函数，有：

进一步地，求解得到桩芯土塞径向和环向位移分别为：

式中I0(·)为零阶第一类变形Bessel 函数。

将式（29）和（30）代入式（9）中，可求得：

2.3 半埋入式管桩桩身振动方程的求解

将式（23）和（33）代入式（5）并整理可得：

基于此，可求得转角、弯矩和剪力的表达式分别为：

进一步地，式（35）～（38）可整理为如下矩阵形式：

在局部坐标系下，层状土中第i层段桩身上下两端的水平位移、转角、弯矩和剪力之间的关系可表示为：

根据桩段间连续条件，在整体坐标系下采用传递矩阵法可求得管桩桩底和桩顶的水平位移、转角、弯矩和剪力之间的关系为：

式中T={TmTm-1…Ti…T2T1}。

由于管桩桩底为固定约束，进而将式（12）和（13）代入式（41）中，可得：

综上，可进一步求得层状土中半埋入式管桩桩顶水平阻抗KQU的表达式为：

式中Κr和Κi分别代表桩顶的水平动刚度和动阻尼。

3 算例分析

本文算例模型将基于前述层状黏弹性土中半埋入式管桩水平振动力学模型和推导所得对应桩顶水平动力阻抗解析解答展开。其中，将地基土体沿纵向分为3层，如图1所示，由地基底部自下而上分别为l1，l2和l3。前述解析解答推导过程中所采用的频率为圆频率ω，而在后续分析中采用频率f=。此外，本文采用MATLAB 软件对式（43）所得解进行计算。如无特殊说明，算例模型具体参数取值［24］如下：

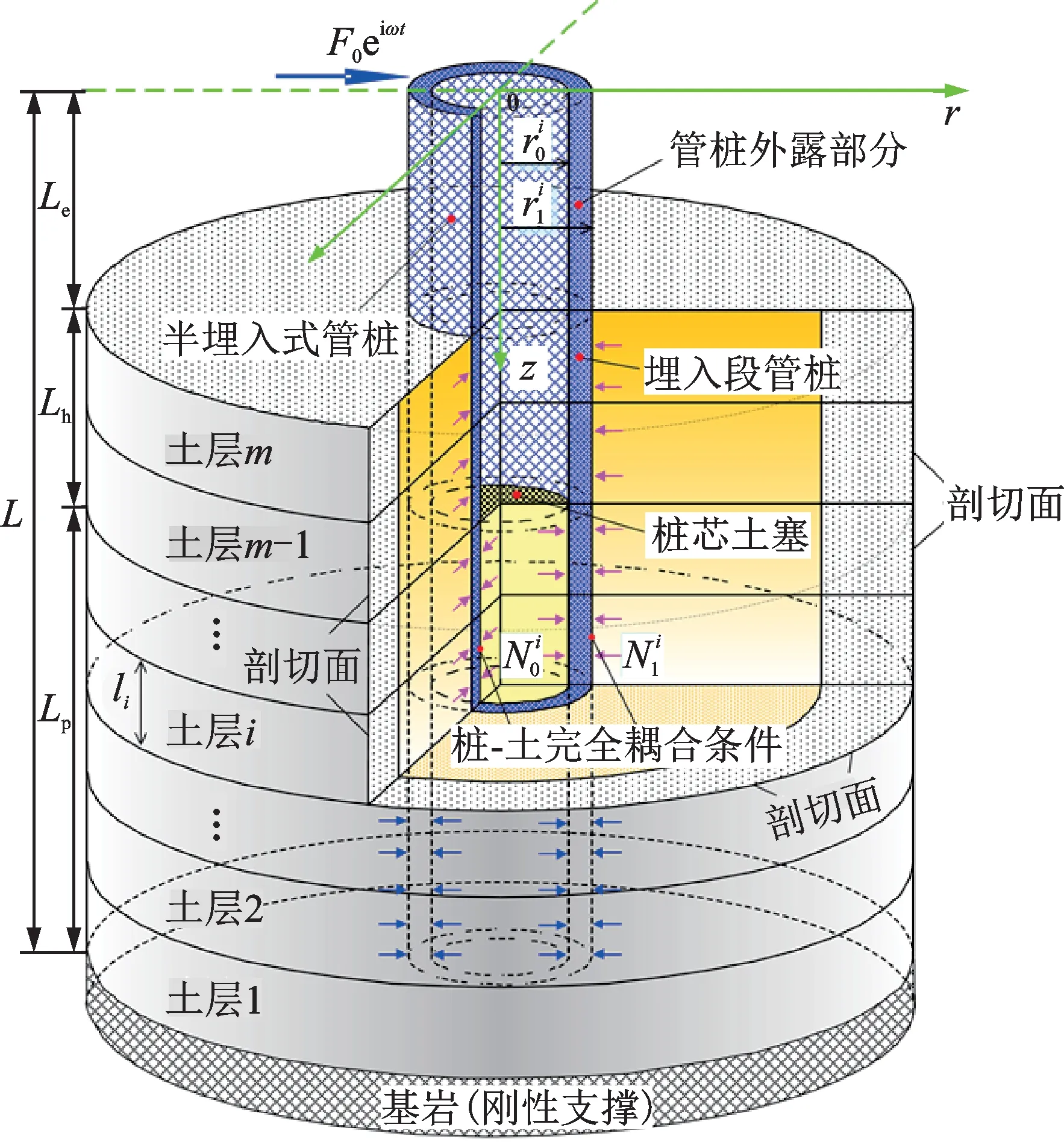
图1 层状土中半埋入式管桩水平振动力学模型Fig.1 Dynamic model of horizontal vibration of pipe pile partially embedded in layered soil

3.1 解析解答合理性验证

为了验证本文所推导的层状黏弹性土中半埋入式管桩水平振动动力阻抗解析解答的合理性，将本文解与已有相关解析解答进行退化对比验证。具体地，令Le→0 m，Lh→0 m，m=1，m，将本文层状土中半埋入式管桩水平振动解析模型退化至文献［32］中所述黏弹性土中实体桩水平振动工况中，并与已有文献解［32］进行对比。本文退化解与已有文献解［32］在3 种不同桩-土弹性模量比条件下的对比情况如图2 所示。由图2 可见，本文推导所得的层状黏性土中管桩桩顶水平阻抗退化解与已有文献解［32］吻合良好。

图2 本文退化解与已有文献解［32］对比情况（Le→0 m，Lh→0 m，m=1→0 m）Fig.2 Comparisons of degenerated solution in this paper with existing solution in reference［ 32］（Le→0 m，Lh→0 m，m=1，→0 m）

3.2 半埋入式管桩桩顶水平阻抗影响因素分析

图3 所示为埋入比变化对半埋入式管桩桩顶水平阻抗的影响情况。其中，Le/L表示管桩埋入线以上部分长度与总桩长之比。由图3 可见，在其他条件不变的情况下，埋入比变化对半埋入式管桩桩顶水平阻抗的影响显著。具体地，随着埋入比的增大，桩顶水平动刚度和动阻尼幅值增大。

图3 埋入比对桩顶水平阻抗的影响Fig.3 Influence of embedment ratio on the horizontal impedance of pile head

图4 和5 所示分别为层状桩周土中各层段土体弹性模量变化对半埋入式管桩桩顶水平阻抗的影响情况。由图4 可见，在其他条件不变的情况下，随着表层土体弹性模量的增大，半埋入式管桩桩顶水平动刚度和动阻尼幅值亦增大。不同地，从图5 中不难看出，桩周土中、下层土体弹性模量变化对半埋入式管桩桩顶水平动刚度和动阻尼的影响均可忽略。这表明桩周土中的表层土体相对于中、下层土体对半埋入式管桩桩顶水平振动特性的影响更为显著。

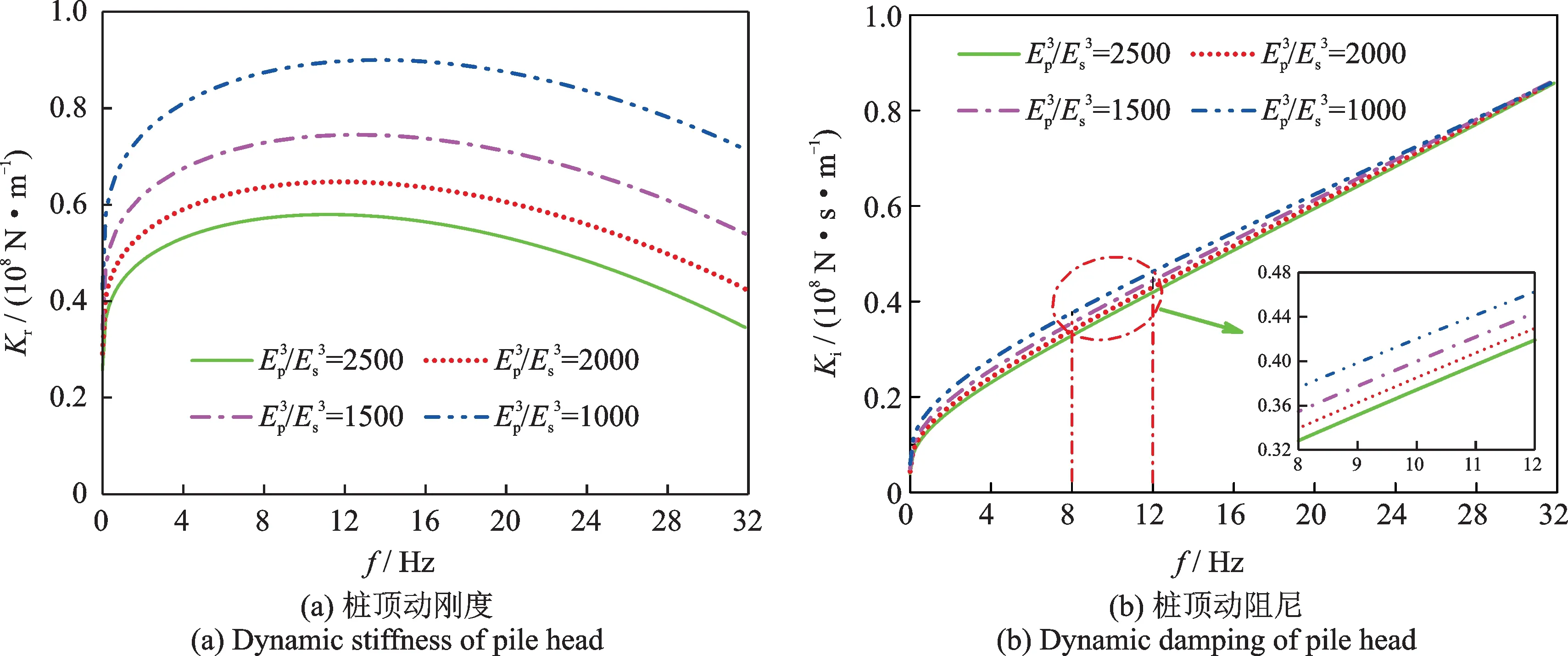
图4 表层土体弹性模量对桩顶水平阻抗的影响Fig.4 Influence of elastic modulus of surface soil layer on the horizontal impedance of pile head

图6 所示为土塞高度Lp变化对半埋入式管桩桩顶水平阻抗的影响情况。由图6 可见，在其他条件不变的情况下，随着土塞高度的减小，半埋入式管桩桩顶水平动刚度幅值减小，而桩顶水平动阻尼幅值随土塞高度的减小而增大。

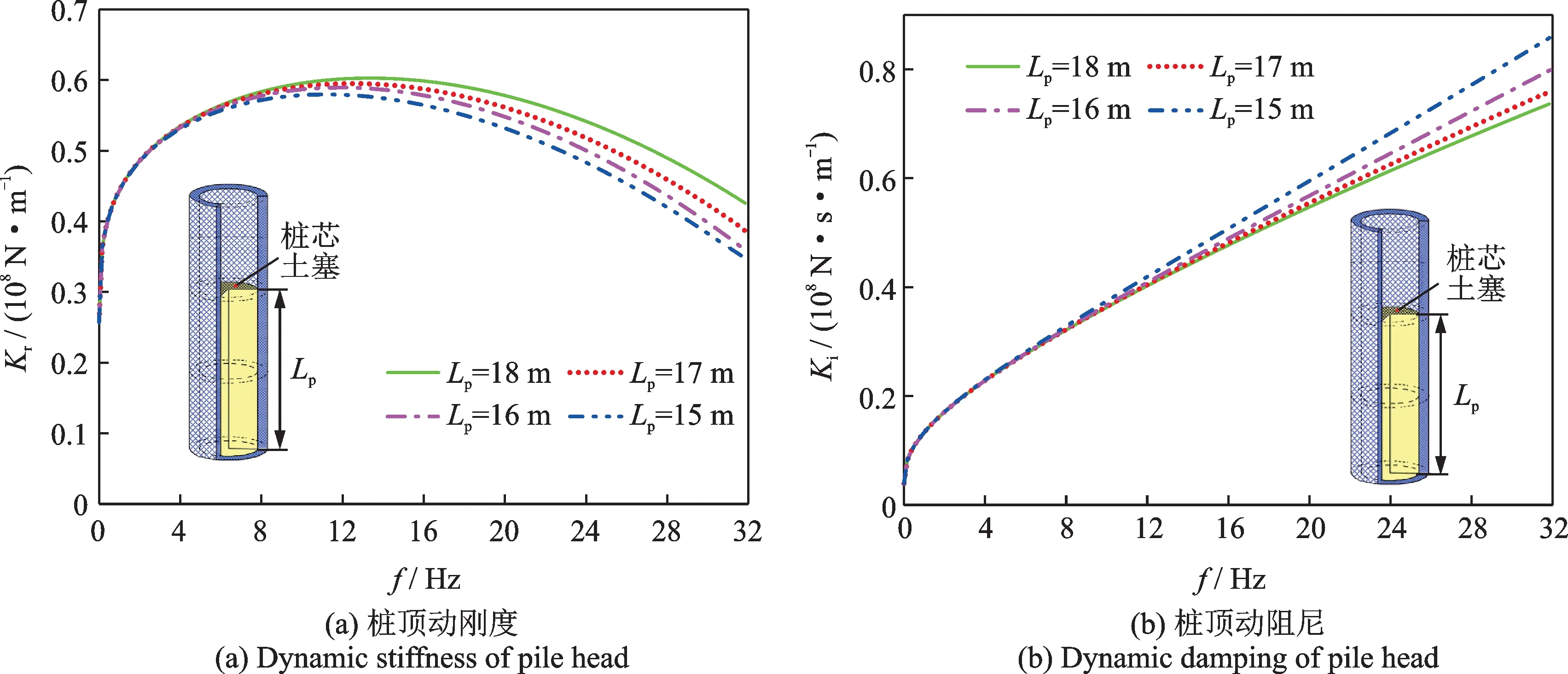
图6 土塞高度对桩顶水平阻抗的影响Fig.6 Influence of soil plug height on the horizontal impedance of pile head

4 结论

本文基于Novak 平面应变理论，综合考虑半埋入式管桩土塞效应的影响，建立了层状黏弹性土中半埋入式管桩水平振动分析模型，推导出了层状土中半埋入式管桩桩顶水平阻抗解析解答，并探讨了管桩埋入比、各层土体弹性模量和土塞高度对半埋入式管桩桩顶水平阻抗的影响规律，计算分析结果表明：

（1）埋入比变化对半埋入式管桩桩顶水平阻抗的影响显著。具体地，随着埋入比的增大，桩顶水平动刚度和动阻尼幅值增大。

（2）随着表层土体弹性模量的增大，半埋入式管桩桩顶水平动刚度和动阻尼幅值均显著增大，而桩周土中、下层土体的此种影响可忽略。

（3）随着土塞高度的减小，半埋入式管桩桩顶水平动刚度幅值减小，而桩顶水平动阻尼幅值随土塞高度的减小而增大。

（4）通过与已有解进行退化对比分析，验证了本文推导所得的对应解析解答的合理性和精度，可为相关工程设计与实践提供参考。