基于神经网络模型的预拌流态土剪切特性研究
高 磊,袁 泽,贺敬绪,刘永季,招 松
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210024;2.南京奥体建设开发有限责任公司, 江苏 南京 210019;3.中建八局第三建设有限公司,江苏 南京 210046)
随着我国经济的快速发展,建筑基坑工程中开挖出了大量工程废土,为充分利用这些工程弃土,降低工程成本[1-2],常采用土体固化的方法[3],将废土、固化剂和水等材料充分拌和后形成固化土,与工程弃土相比显著提高了力学性能[4]。高磊等[5]将玄武岩纤维丝掺入黏土中进行直剪试验,得出随着纤维掺量增加,土体粘聚力不断增加的结论。杨爱武等[6]通过三轴试验对固化土的剪切性能展开研究,结果表明应力峰值随着养护龄期的增大而增大,残余强度与养护龄期成反比,与剪切位移成反比。胡亚元等[7]对纤维加筋淤泥固化土进行排水三轴试验,结果显示随着纤维掺入比增加,粘聚力显著增长而内摩擦角几乎不变。朱彦鹏等[8]开展了风化砂岩流态土剪切试验,分析抗剪强度的影响因素及显著性大小,并给出了抗剪强度的回归方程。赵卫国等[9]揭示了固化土颗粒间胶结作用的机理。
神经网络模型是一种基于数据处理的分析方法,通过对训练集数据进行分析,从而获取预测值,有助于了解掌握数据的变化规律,提高试验效率[10-11]。谢文强等[12]基于孔压静力触探获得的端阻力和孔隙水压力数据,利用人工神经网络模型,成功预测了黏土的不排水抗剪强度。Hasanzade-Inallu[13]结合LM算法精准预测出了FRP筋和无箍加固混凝土梁的抗剪强度。肖治宇等[14]进行了非饱和残坡积土的强度试验,并建立了非饱和残坡积土强度随含水率变化的BP神经网络模型,较好地预测出试验范围内任意含水率下对应的土体应力-应变关系。
本文基于南京河西某基坑肥槽回填工程,将开挖出的工程弃土与M32.5水泥和水充分拌和制成具有一定流动性的预拌流态土,对预拌流态土进行直剪试验,从剪应力-剪切位移曲线、峰值强度和粘聚力的角度研究预拌流态土的剪切性能;并在室内试验的基础上,建立并训练出收敛速度快且预测精度高的剪应力-剪切位移神经网络预测模型,并将预测值与实测值对比分析,验证了模型的可靠性。
1 预拌流态土直剪试验
1.1 试验材料
本试验选用的土体为南京河西某基坑工程开挖出的灰褐色细粉砂,进行原状土干密度试验、相对密实度试验、直剪试验、有机质含量测定试验,得到土的基本物理性能指标见表1。

表1 土的基本物理性质指标Tab.1 Basic physical property indexes of soil
本试验所选用的水泥为衬砌水泥,代号为M32.5,是硅酸盐水泥熟料、石膏和活性混合材料或工业废料磨细制成的水硬性胶凝材料,其中矿渣掺量为42%,硬石膏掺量为6%,具体的物理性能指标见表2。

表2 试验所用水泥的物理性能指标Tab.2 Physical performance indexes of cement used in the test
1.2 试验流程
本文的预拌流态土是指将土体与固化剂和水搅拌充分后,经过坍落度测定试验满足扩展度要求的混合土体。搅拌均匀后分层浇入61.8 mm×20 mm的环刀内,辅以插捣减少试样内空隙,制备完成后放入养护箱(养护箱内环境湿度控制为95%,温度控制为20 ℃)内,待养护至指定龄期后进行直剪试验。烘干后的原状土,在不掺入固化剂的情况下,当含水率达到33%时,土体接近“饱和”,故以33%作为本次试验的初始含水量。选定本次试验的固化剂配比,在初始含水率33%的基础上分别掺入0.6、0.8、1.0水灰比的水与固化剂。根据《预拌流态固化土填筑技术标准》[15]中给出预拌流态土的固化剂配比范围大致为7%~25%,本次试验选用的水泥固化剂配合比为8%、11%、14%、17%和20%。依据上述配比方案,每种配比下的试样均养护7、14与28 d,并在指定龄期进行直剪试验,采用快剪试验的方式进行试验,以1.2 mm/min的速率剪切,剪切时长为5 min。
1.3 试验结果分析
1.3.1 剪切曲线
记录直剪试验过程中的百分表读数,得到剪切位移,再通过钢环系数计算得出剪切应力,以剪切位移为横坐标,剪切应力为纵坐标,可得到预拌流态土试样的剪切应力-剪切位移曲线。
图1为预拌流态土典型的剪应力-剪切位移曲线。由图1(a)可得,8%水泥配合比、0.6水灰比的土样在养护7 d时,100 kPa垂直压力下剪应力有峰值,在200、300和400 kPa垂直压力下剪应力峰值不明显。由图1(b)可得,14%水泥配合比、0.6水灰比的土样在养护14 d时,100、200、300和400 kPa垂直压力下剪应力有明显峰值。

注:图(a)和图(b)命名格式为“水泥配合比-水灰比-养护龄期”。图1 预拌流态土典型剪应力-剪切位移曲线Fig.1 Typical shear stress-shear displacement curve of premixed fluid soil
1.3.2 抗剪强度
预拌流态土的抗剪强度为剪切应力-剪切位移曲线上峰值点或稳定值所对应的剪应力大小,若未出现明显峰值点,则取剪切位移为4 mm处对应的剪应力作为抗剪强度,抗剪强度的大小与水泥配合比、水灰比、养护龄期和垂直压力相关。图2为本次试验中养护14、28 d土样在不同水灰比与垂直压力情况下抗剪强度。
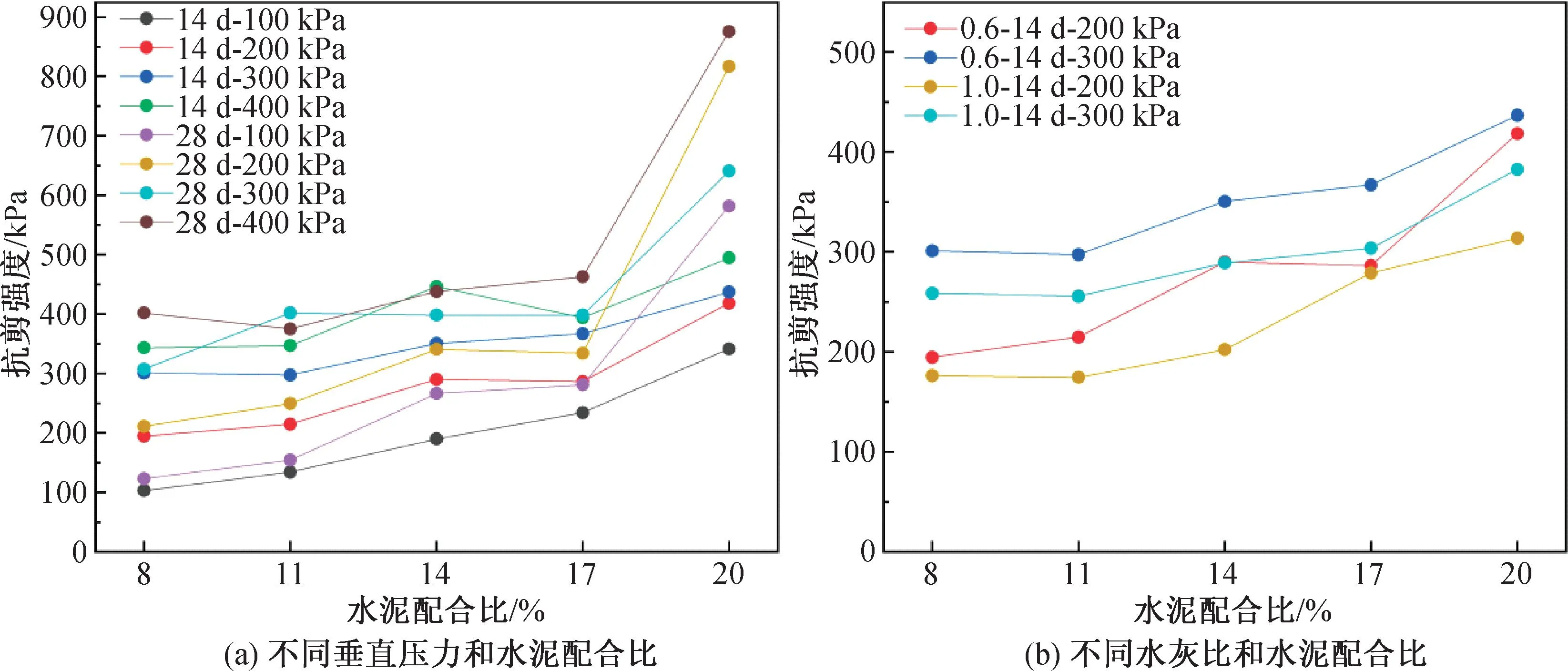
图2 土样的抗剪强度Fig.2 Shear strength of soil samples
由图2(a)可得,养护龄期为28 d土样的抗剪强度大于养护龄期为14 d时的强度。在同一水泥配合比下,当垂直压力从100 kPa增加至400 kPa时,试样的抗剪强度逐渐增加,且各级垂直压力下抗剪强度增加的幅度较为接近。随着试样的水泥配合比从8%逐渐增加至20%,抗剪强度整体上逐渐增加,其中,当水泥配合比从8%增加至17%时,大部分试样抗剪强度的增幅较为平稳,不会出现强度骤增的情况,而当水泥配合比从17%增加至20%时,试样的抗剪强度增幅较大,出现了强度骤增现象,并且这种强度骤增现象在养护龄期为28 d、垂直压力为300和400 kPa时更容易出现,这是因为当水泥配合比增加至20%时,养护28 d的试样强度增大,在直剪试验过程中难以被剪切破坏,故试样的抗剪强度会出现骤增。由图2(b)可得,当水灰比从0.6逐渐增加至1.0时,对于同一水泥配合比和垂直压力下的试样,峰值强度逐渐减小。图2的试验数据个别点出现偏离,可能是试样制备时搅拌不均导致的。
1.3.3 粘聚力
粘聚力为土体重要抗剪强度指标,本次试验中,以养护7与14 d时试样的粘聚力为例,获取粘聚力与养护龄期、水灰比之间的规律。由图3可得,随着养护龄期从7 d增加至14 d,试样的粘聚力逐渐增加。随着水泥配合比从8%增加至20%,预拌流态土的粘聚力整体上逐渐增加,当水泥配合比为8%和11%时,养护龄期为7 d的试样之间粘聚力差距较小,但随着养护龄期增长为14 d,各水泥配合比下试样之间粘聚力差距逐渐增加,并且这种差距在水泥配合比为17%和20%时最明显。随着水灰比由0.6逐渐增加至1.0,相同龄期和水泥配合比下试样的粘聚力逐渐减小。
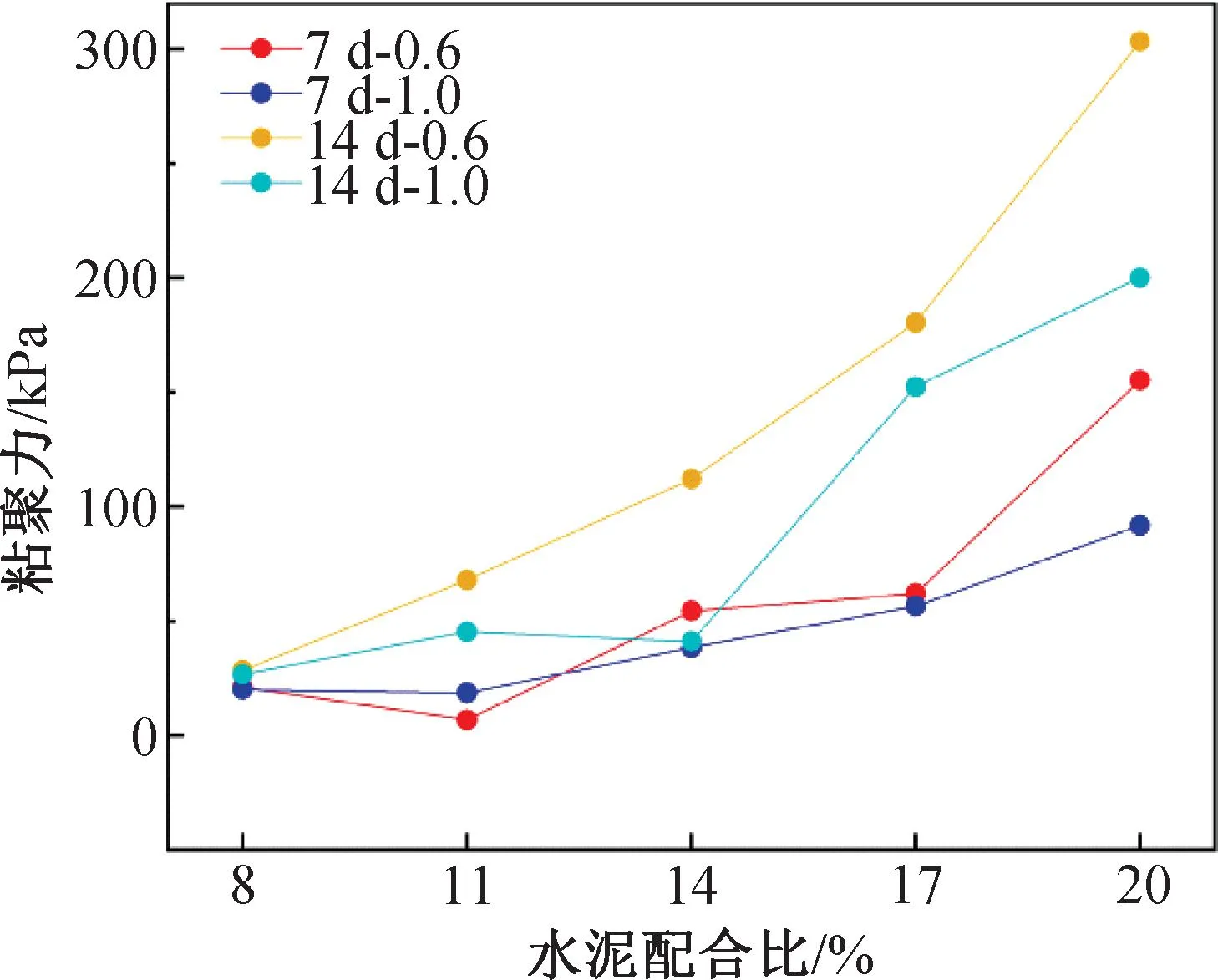
图3 预拌流态土的粘聚力与水泥配合比的变化曲线Fig.3 The variation curve between cohesion and cement content of premixed fluid soil
2 预拌流态土剪应力-剪切位移神经网络预测模型
2.1 神经网络原理
BP(Error Back Propagation)神经网络为多层前向神经网络,是一种强调网络采用误差反向传递的学习算法,网络结构由输入层、隐藏层和输出层组成,数据从输入层通过隐含层逐层向后传播,各层之间通过权值相连接,在训练网格权值时,沿着减少误差的方向,从输出层开始逐层向前修正网络连接权值,最终减小误差,该神经网络适用于求解非线性问题且容错性高。
2.2 建模方案
由直剪试验数据可得,预拌流态土的剪切性能受剪切位移、水灰比、养护龄期、垂直压力和水泥配合比多个因素直接影响,上述参数之间为复杂的非线性关系,适用于神经网络输入层数据的选择标准。故以剪切位移、水灰比、养护龄期、垂直压力和水泥配合比作为神经网络输入层,对应的直剪过程中的剪切应力作为输出层。
随着垂直压力的增加,剪切破坏位移会逐渐后移;对于同一配合比试样,养护龄期越长则剪切破坏出现的时间越晚。为判断本文建立的神经网络模型效果,选取11%-0.8配比土样在7、14和28 d时的3组试验数据作为预测集数据,余下的42组数据选为训练集数据,本文神经网络模型的数据集划分见表3。

表3 神经网络模型建模方案Tab.3 Modeling scheme of neural network model
隐含层可为一层或两层及以上,足以展现出优秀的预测性能,而隐含层节点数尤为重要,节点数过少,则网络学习效果差,节点数过多,则网络会呈现出过拟合状态,现对于隐含层的确定方法较为多样,本文依据经验公式和试算法相结合来确定合理的隐含层节点数。本文输入层节点数为5,输出层节点数为1,依据经验公式得出隐含层节点数大致为3以上的自然数,再结合多次试算,最终得出本文神经网络隐含层节点数为5时拟合效果最佳,具体的神经网络建模见图4。
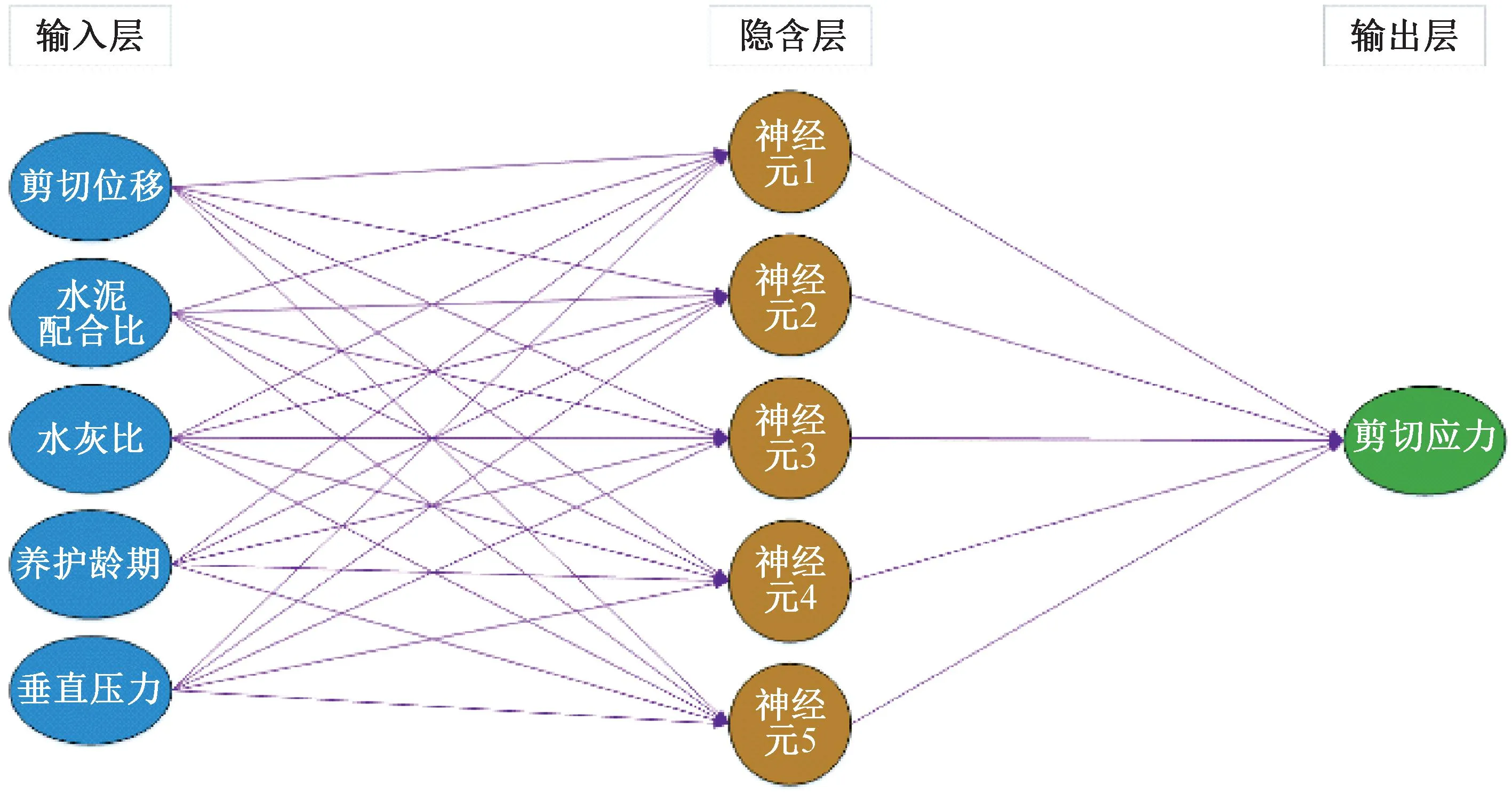
图4 神经网络建模方案Fig.4 Scheme of neural network modeling
(1)
式中,m为输入层节点数,n为输出层节点数,a为1~10之间的常数。
神经网络在进行训练学习时,若各层节点的数据为不同的数量级,则网络学习效率不佳,减缓最速下降法的迭代速度,降低精度。本次神经网络的输入层和输出层存在着不同数量级的数据,如垂直压力为102量级,而水灰比、剪切位移往往为10-1数量级,因此,为避免神经网络迭代过程中出现权重两极分化的问题,将试验数据进行归一化,缩放至[0,1]范围内。
(2)
式中,x为原始数据,y为归一化处理后的数据,max (x)和 min (x)分别代表原始数据中的最大值和最小值。
对于本文BP神经网络预测模型,采用均方根误差(RMSE)和相关系数(R2)来评价其预测性能,其中,RMSE预测值与实测值的误差平方根的均值,体现了神经网络预测效果的稳定性;R2为0~1之间的数,越贴近于1则表明预测效果越好。
(3)
(4)

3 模型结果分析
3.1 模型误差
将42组预拌流态土直剪试验数据放入本文所建的神经网络模型中进行训练,余下的3组试验数据选作为预测集,对模型的预测精度进行检验。图5为本文神经网络模型的误差分布图,数据点越接近1∶1线则神经网络模型对于该点的预测精度越高,本次神经网络模型预测结果详见表4。

图5 误差分布图Fig.5 Error distribution diagram
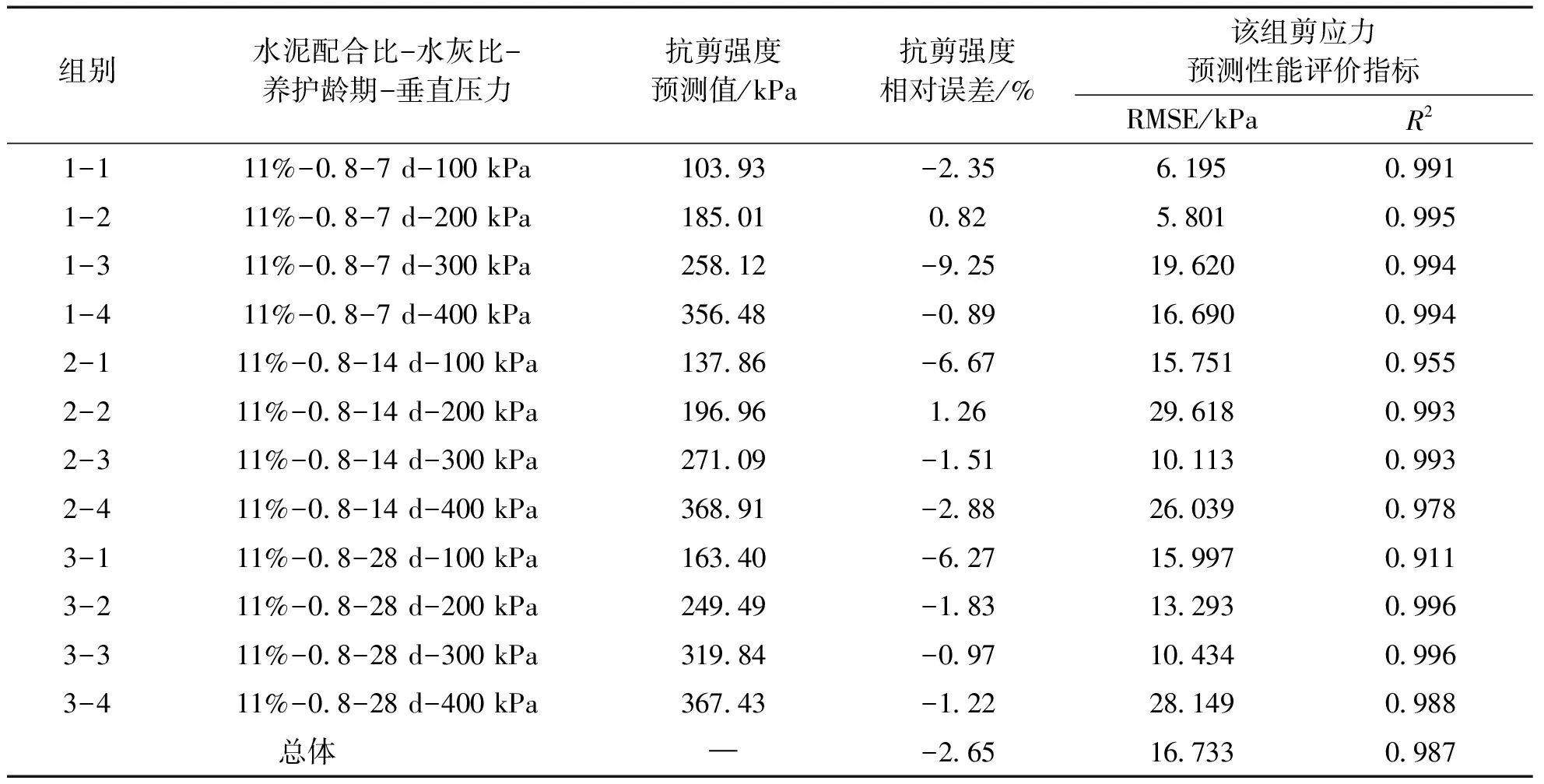
表4 神经网络模型预测性能检验表Tab.4 Performance checklist of Neural network model predictions
由图5可得,大部分试验数据点都是紧贴1∶1线,预测结果较好,存在个别组数据点稍偏离1∶1线。依据表5可得,各垂直压力下剪切位移-剪应力曲线预测点的R2均为0.9以上,同时整体数据的R2达到了0.987,表明本次神经网络结果拟合效果较好,预测剪应力-剪切位移曲线与实测剪应力-剪切位移曲线的趋势较为相似。RMSE在垂直压力较小时其数值也较小,表明预测曲线与实测曲线较为贴近;在垂直压力较大时数值较大,而峰值剪应力点的误差却非常小。

表5 粘聚力实测值与预测值结果对比Tab.5 Comparison of measured results and predicted cohesive forces
3.2 剪切曲线特征分析
神经网络模型通过特定水泥配合比、水灰比、养护龄期、垂直压力、剪切位移求得相应的剪切应力,进而可得到剪应力-剪切位移曲线。图6为本次神经网络模型得到的剪应力-剪切位移曲线和实测数据得到的剪应力-剪切位移曲线对比。

图6 神经网络模型预测曲线与实测曲线对比Fig.6 Comparison curve of predicted curves obtained by neural network model and measured curves
由图6可得,养护龄期为7、14和28 d时,四种压力下剪应力-剪切位移预测曲线与实测曲线规律一致。
3.3 抗剪强度及粘聚力
由表4可得,本文所建立的神经网络模型对于峰值强度的整体预测误差仅为-2.65%,预测精度较高。基于本文所建立的神经网络模型,并不可直接得到某一配比下土样的粘聚力,需通过预测得到的峰值强度间接得到。通过分析“11%-0.8-7 d”、“11%-0.8-14 d”和“11%-0.8-28 d”土样各垂直压力下预测得到的抗剪强度,通过抗剪强度-垂直压力曲线可得到粘聚力预测值,表5为粘聚力实测值与预测值的结果对比。
由表5可得,基于神经网络预测模型得到粘聚力预测值与实测值较为接近,三组粘聚力预测结果的相对误差均控制在了10%以内,其中,“11%-0.8-7 d”的土样粘聚力预测结果最优,粘聚力预测值的相对误差仅为-0.82%。因此,通过本文神经网络模型对土体的抗剪强度和粘聚力进行预测是合理的,预测结果精度较高。
4 结论
1)预拌流态土的抗剪强度和粘聚力会随着水泥配合比、养护龄期的增加而增加,随着水灰比的增加而减小,其中,当水泥配合比达到20%时,抗剪强度增幅较大。
2)对于预拌流态土的剪应力-剪切位移,提出了BP神经网络预测模型,以剪切位移、水泥配合比、水灰比、养护龄期和垂直压力为输入层,隐含层神经元数量设为5,以剪切应力为输出层,分析得到神经网络模型预测结果的整体RMSE和R2分别为16.733 kPa和0.987,具有较高的预测精度。
3)本文建立的预拌流态土剪应力-剪切位移神经网络预测模型对抗剪强度和粘聚力预测效果较优,预测相对误差控制在了10%以内,预测效果最优的点预测误差不足1%。

