基于终端滑模的无人机编队协同控制
段 凯,高晗威,王 珂,孙铭阳,郭 永
(1.西北工业大学,陕西西安 710000;2.北京宇航系统工程研究所,北京 100000;3.航天科工智能运用与信息安全研究院(武汉)有限公司,湖北武汉 432200)
0 引言
无人机的编队飞行控制在军事和民用领域都有广泛的应用,近年来已经引起业内广泛关注[1]。目前新兴的基于一致性理论的编队方法很好地解决了编队信息共享的问题,为无人机编队控制提供了理论依据,并在解决关键技术和难点方面开始发挥独特的优势[2-6]。
文献[7]针对具有不确定外部扰动的四旋翼,提出了基于终端滑模的编队控制器,实现了有限时间控制、路径精确跟踪和误差快速收敛。文献[8]针对存在模型不确定性和风场扰动的旋翼无人机编队设计了1种超螺旋终端滑模控制方法,利用自适应控制估计模型不确定性和风扰的未知界限,最终实现了跟踪路径误差的有限时间稳定。文献[9]针对具有不确定外部扰动的四旋翼无人机的位置回路和姿态回路,分别设计类似于超螺旋算法的积分滑模控制器,实现了整个系统的固定时间控制,并设计李雅普诺夫函数进行证明。但是上述的研究大多集中于旋翼布局这种相对简单的飞机进行编队控制器设计,而对于具有高度非线性和耦合的固定翼飞机的研究却较少涉及[10-11]。
滑模控制(SMC)由于具有优秀的抗干扰性能以及较强的鲁棒性,而成为最流行的控制方法之一[12-13]。与传统的滑模控制相比,非奇异终端滑模控制能够使得编队误差在有限时间内更快地收敛,且可以克服传统终端滑模所存在的奇异现象,因而被广泛应用。文献[714]针对具有模型不确定性和外部扰动的四旋翼编队,设计结构更加紧凑的非奇异快速终端滑模控制器,并使用改进的趋近律加快系统远离滑动模态时的趋近速度,有效消除抖振。文献[15]对于存在模型不确定以及外界扰动的多无人机进行研究,提出了1 种自适应非奇异终端滑模控制技术,用于实现参数不确定的无人机系统的有限时间稳定。文献[16]针对无人机机动任务的复杂性设计1 种新的机动策略,提出具有良好性能的新型全局快速终端滑模控制方法,并设计李雅普诺夫函数进行证明。
然而,上述以及多数文章中对于无人机编队的研究往往忽略输入约束问题。无人机作为1 个机械实体,不可能具有无限制的控制力,且固定翼飞机的推力装置也只能输出推力,而不能提供后退或者减速的力,所以固定翼飞机的控制输入存在非对称受限的情况[17-18]。因此,在设计控制律时必须考虑到这些实际情况,否则设计的控制律不具有实用性。
本文考虑具有输入约束的固定翼无人机模型,提出1 种固定翼无人机非奇异终端滑模编队控制器,本文做出的工作如下:
1)将固定翼飞机的推力与阻力分别建模,不同以往的文章中将其一同建模,这样更加接近真实的飞机,且考虑输入的受限情况,更具有实际意义;
2)提出1种全局快速非奇异终端滑模面,既能使得在远离滑动模态时系统速度加快,又能避免传统终端滑模产生的奇异性,且形式相较于以往的非奇异终端滑模更加简单,易于工程实现。
3)提出1种抗饱和辅助系统,用以解决输入受限问题,并对于外部存在的不确定干扰,设计了自适应律进行估计,使得系统具有较强的鲁棒性。
1 准备工作和模型描述
1.1 图论
文中,ℝn×m表示n×m实数矩阵的集合,ℝn表示n维向量。

1.2 无人机单机及编队系统模型
建立考虑外部扰动和输入受限的无人机模型,第i架无人机的非线性运动学与动力学模型如下:
定义:
考虑输入受限,则第i架无人机的模型可以整理为:

文中的无人机编队是1 个由N架跟随者无人机与1 个虚拟领航者构成的多无人机系统,则建立控制目标如下:
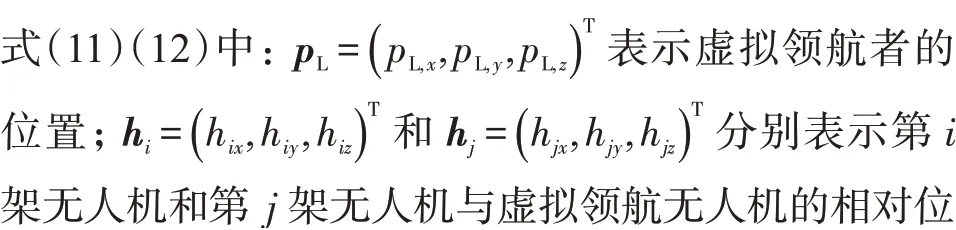
则可定义编队中第i架无人机的联合位置误差为:
由上式可以看出,当联合位置误差ei收敛到0时,各无人机将按照预设的队形收敛到各自的期望位置,并形成期望队形。
定义编队联合位置误差与相对距离矩阵为:
则整个编队联合误差为:
记:
则式(16)可以表示为:
对式(20)求导可得:

本文的控制目标:针对一类含有外部时变扰动且控制输入受限的无人机编队系统,设计自适应非奇异终端滑模控制器,使无人机编队能够跟踪上期望指令。
2 自适应非奇异终端滑模控制器设计
2.1 抗饱和辅助系统设计
设计抗饱和辅助系统如下:
式(23)中:c1、c2都为正整数,且c1、c2的选值应当尽量大,这样可以使得系统退饱和迅速。
对式(24)求导可以得到:
式(25)即为引入抗饱和辅助系统后的系统方程。
2.2 自适应非奇异终端滑模控制器设计
设计全局快速非奇异终端滑模面如下:
式(26)中:k1,k2为正整数,且k1>0.5。
对式(26)求导可以得到:
设计控制器以及自适应律如下:
式(28)(29)中:k3、k4、γ都为正整数,且k3>0.5。
2.3 稳定性证明

将控制律代入上式:
由
得到:
将自适应律代入上式得:
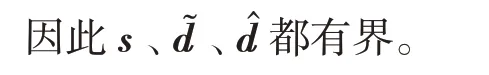
构造另一李雅普诺夫函数:
求导可得:
由文献[19]中引理可得:
式(38)中,κ=0.278 5。
由杨氏不等式[19]得:
代入式(37)可得:
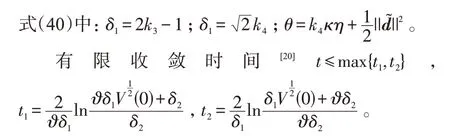
因此,滑模面在有限时间t内稳定到原点附近的1个小邻域内,设这个邻域的界为ψ:
移项得:
构造李雅普诺夫函数如下:
求导可得:
由杨氏不等式:
由文献[19]中引理可得:
代入式(44)得:

故整个系统将在tm≤t+t′后有限时间到达稳定。证明完毕。
3 仿真分析
3.1 仿真条件
本节给出1个仿真例子来验证所提编队协议的有效性。考虑1 架虚拟领航者无人机和3 架跟随无人机,用所提出的控制方法来实现无人机编队飞行。
表1列出各架无人机的初始信息。无人机编队的期望队形在编队误差为0 的理想情况下,是以3 架跟随无人机为顶点、虚拟领航者为中心的等边三角形。
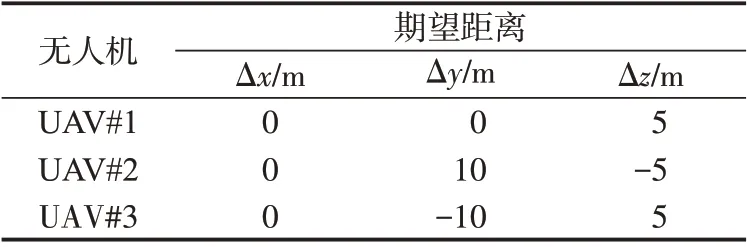
表1 编队队形Tab.1 Formation
仿真中设计的编队队形中,各个跟随无人机与虚拟领航无人机的期望相对距离如表1 所示;编队中各个成员的初始参数如表2所示。
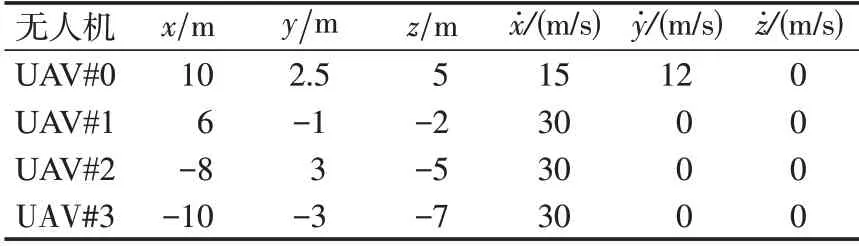
表2 无人机编队初始参数Tab.2 Initial parameters of UAV formation

表3 控制参数Tab.3 Control parameters

3.2 仿真结果
仿真结果如图1~12 所示。图1~3 分别表示编队中3 架无人机的联合位置误差,在设计的输入受限的自适应非奇异终端滑模控制器的作用下,联合位置误差的跟踪曲线平滑且无超调,并且所有无人机的稳态误差均在10-3m 以内。图4~6 分别为3 架无人机的联合速度误差,可以看出联合速度误差以较快的速度收敛,且所有无人机的稳态误差均在10-3m/s以内。
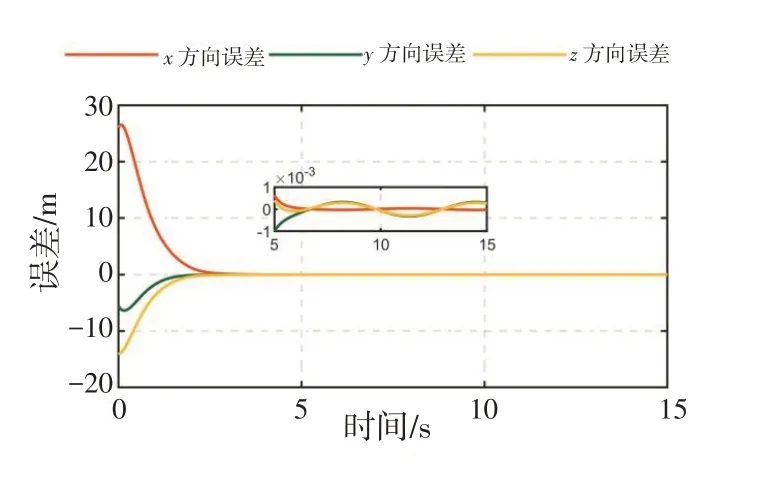
图1 无人机1联合位置误差Fig.1 Joint position error of UAV#1
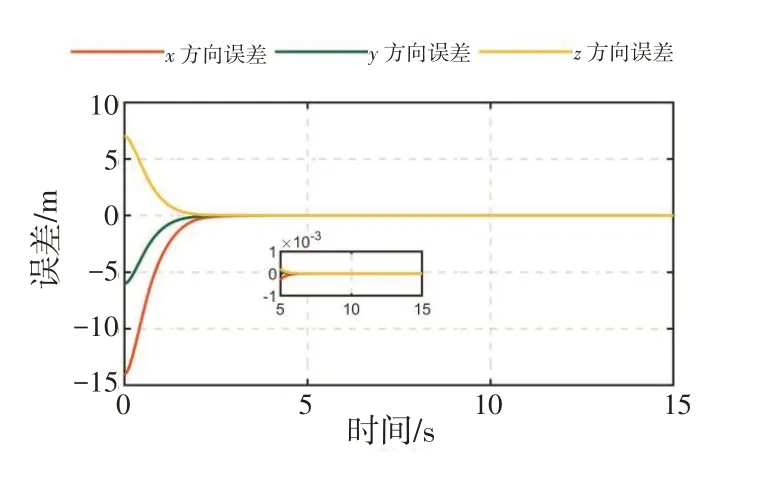
图2 无人机2联合位置误差Fig.2 Joint position error of UAV#2
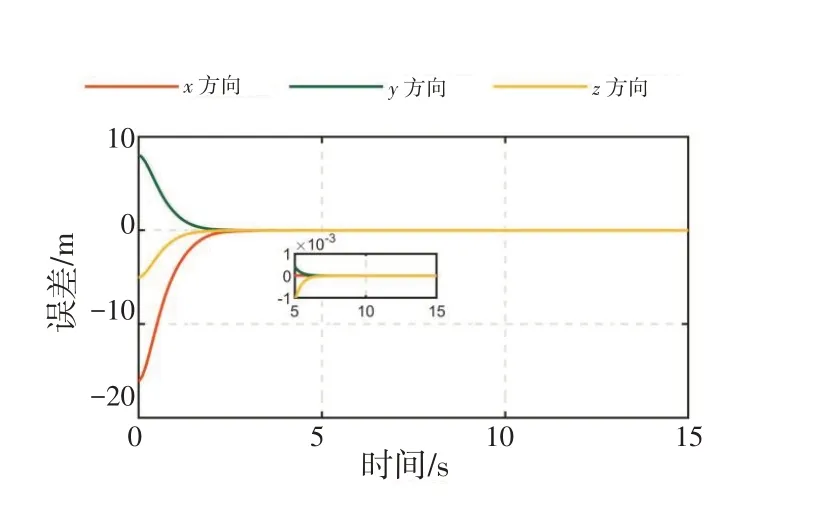
图3 无人机3联合位置误差Fig.3 Joint position error of UAV#3
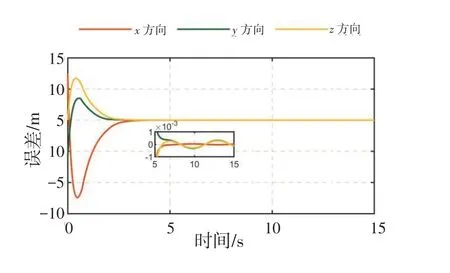
图4 无人机1联合速度误差Fig.4 Joint speed error of UAV#1
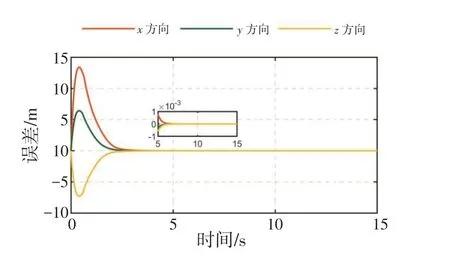
图5 无人机2联合速度误差Fig.5 Joint speed error of UAV#2
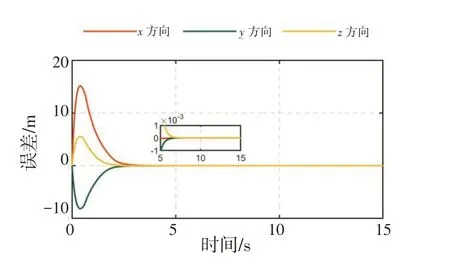
图6 无人机3联合速度误差Fig.6 Joint speed error of UAV#3
图7~9分别为3架无人机实际中与自身在编队中的理想位置的绝对位置误差,可以看出其收敛的时间与联合位置误差是一致的,且收敛过程无超调,稳定误差在10-3m以内。

图7 无人机1绝对位置误差Fig.7 Absolute position error of UAV#1

图8 无人机2绝对位置误差Fig.8 Absolute position error of UAV#2
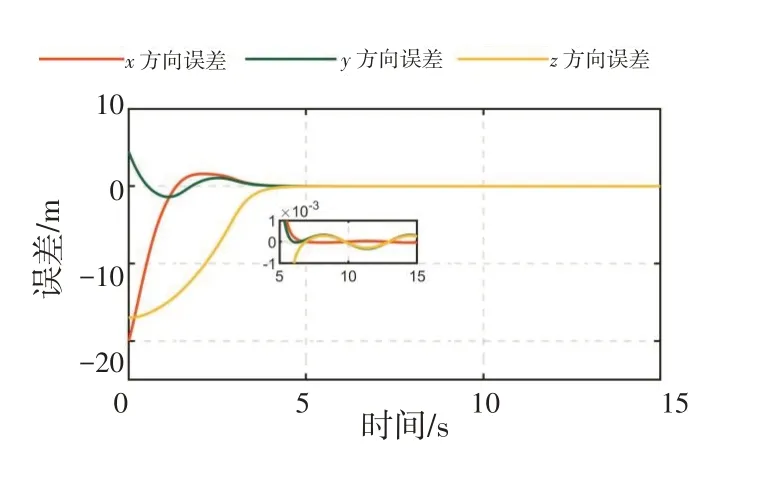
图9 无人机3绝对位置误差Fig.9 Absolute position error of UAV#3
图10~12 分别为3 架无人机的3 个方向的控制力变化情况,其中推力范围在0~200 N以内,其余两方向控制力在-40~40 N 以内,满足所设计的输入受限条件。由于系统在3 个方向上存在正弦波形式的扰动,其控制力呈现一定的波动来抵消扰动,且控制力在波动的过程中保持在输入限制以内。
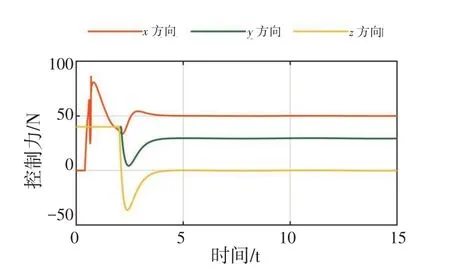
图10 无人机1控制力Fig.10 Control force of UAV#1
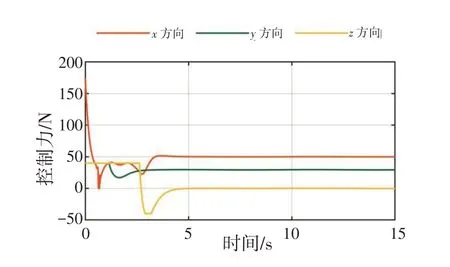
图11 无人机2控制力Fig.11 Control force of UAV#2

图12 无人机3控制力Fig.12 Control force of UAV#3
综上所述,本文提出的输入受限的自适应非奇异终端滑模控制器可以在无人机控制输入受限情况下使无人机编队在指定时间内组成期望队形并跟踪上虚拟领航无人机的轨迹。
4 结论
本文针对具有不确定外界干扰的固定翼无人机编队提出1种新型非奇异终端滑模控制器。为了使控制器更加实用,本文考虑了控制输入约束问题,并设计抗饱和辅助系统来解决该问题。仿真结果表明,辅助系统的性能良好,并证明本文所提的控制方法的可行性与先进性。

