辽东湾粒状海冰弯曲力学行为试验研究

修苑人，李志军，王庆凯，韩红卫

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.东北农业大学 水利与土木工程学院，黑龙江 哈尔滨 150030）

海冰灾害是渤海和黄海北部海域冬季的主要海洋灾害之一。在覆冰海域，海冰可能对船舶、海岸和海上结构物造成破坏，对港口运输、海上油气开采、海洋渔业等经济活动构成严重威胁[1-2]。因此，在冰区船舶和海洋结构物的设计、建造和运行过程中，冰荷载的影响应被重点考虑。弯曲破坏是一种常见的冰破坏模式，常发生于海冰与船舶、斜面护坡、海洋平台抗冰锥体等相互作用时[3-5]。发生弯曲破坏时结构物上的冰荷载通常比其他破坏模式下的冰荷载低得多，因此冰弯曲破坏的低荷载优势在结构物抗冰设计中得到了广泛应用[6-7]。弯曲强度和有效弹性模量是海冰弯曲破坏的两个关键力学参数，对于研究海冰发生弯曲破坏时的力学行为尤为重要[8]。测定海冰的弯曲强度和有效弹性模量的试验主要包括悬臂梁和简支梁试验两类[9]。

海冰作为一种由纯冰、卤水胞、气泡、固体盐等组成的多相复合晶体材料，其力学性质会受到冰晶结构、温度、盐度、密度等冰物理性质的影响[10]。以往的研究多以低温海冰为对象，冰内气泡较少，因此卤水体积曾一度成为评估海冰力学特性的主要物理指标。以往试验结果表明海冰弯曲强度和有效弹性模量随卤水体积的增大而降低[8,11-13]。Timco 等基于全球众多覆冰海域的939 次冰梁试验结果，得到了海冰弯曲强度关于卤水体积分数平方根的负指数关系，在国际上已被广泛使用[14]。渤海海冰温度较高，冰内气体体积较大，因此仅使用卤水体积将会限制对高温海冰力学性质的正确评估[15]。海冰内部的卤水和气体都不具备承受荷载的能力，因而理论上孔隙率作为卤水与气体体积之和，是评估海冰力学性质最理想的物理指标。然而，除了李志军等[16]给出了渤海海冰峰值弯曲强度与孔隙率的试验关系外，很少有研究关注海冰弯曲强度以及有效弹性模量与孔隙率之间的关系。此外，海冰是一种力学性能易受加载速率影响的材料，在不同应变速率下的单轴压缩试验中表现出明显的韧-脆转化特征[15,17]。然而，加载速率是否对海冰的弯曲强度有显著影响？不同的研究得到的结果并不相同。多数研究报道加载速率对海冰弯曲强度影响不显著[10,14,18]，也有试验结果显示海冰弯曲强度随加载速率的增加呈增加[8,12]或呈先增加再降低的规律[6,19]。海冰弯曲破坏对加载速率的敏感性问题仍需试验验证。

全球变暖延长了渤海海冰的冻结期，导致冰层中粒状冰含量呈上升趋势[1,20-21]。以往研究表明粒状海冰的弯曲强度值高于柱状海冰，因此，在工程实践中粒状海冰的弯曲力学行为应引起重视[22-23]。由于关于粒状海冰的弯曲强度和有效弹性模量的研究很少，对粒状海冰弯曲力学行为认识仍显不足，因此需要对渤海粒状海冰的弯曲力学性质进行试验研究。本文在2010－2011 年冬季于渤海辽东湾东部沿岸结冰海域现场取样并针对粒状冰进行了实验室三点弯曲试验。测定了冰样的物理性质并分析了孔隙率和应变速率对冰弯曲强度和有效弹性模量的影响。根据试验结果得到了相应的函数关系，为确定不同条件下粒状海冰弯曲强度和有效弹性模量提供了有力的借鉴。

1 现场取样和冰层物理性质

冰坯取样地点位于辽东湾东部的瓦房店市沿岸海域，此处是我国冬季结冰海域中冰情最重的海区之一（图1（a））。2010 年12 月初该海区海冰进入初冰期，其盛冰期出现在2011 年1 月中旬至2 月中旬，3 月初转入融冰期。本次取样时间为盛冰期的2011 年1 月25 日上午。选择一处平整冰层使用电链锯从中割取冰坯（图1（b））。共采集6块横截面为80 cm × 25 cm（平均冰厚约34 cm）的冰坯用于加工弯曲试样。冰坯含沙量较小，整体颜色为白灰色，从侧面观察发现冰坯在厚度上无明显分层。在现场标记冰坯的顶部和底部，以确保晶体结构观察和实验室弯曲样品加工的正确方向。用塑料布包裹冰坯，随后将其运回低温实验室并储存在-15 °C的低温环境下。

图1 海冰取样点位置及取样现场

为了解冰坯的原位状态，在取冰坯的同时测量了冰层的温度剖面，并沿厚度切割了试样，待其融化后用于测定盐度剖面。海冰的晶体结构可以反映海冰经历的生长状态，也决定了其力学性质是否表现为各向同性。因此，冰晶体切片观测在冰坯运回实验室后在-18 ℃的低温环境下优先进行。取样日上午9 时，冰层的温度剖面、盐度剖面和冰晶体切片照片见图2。

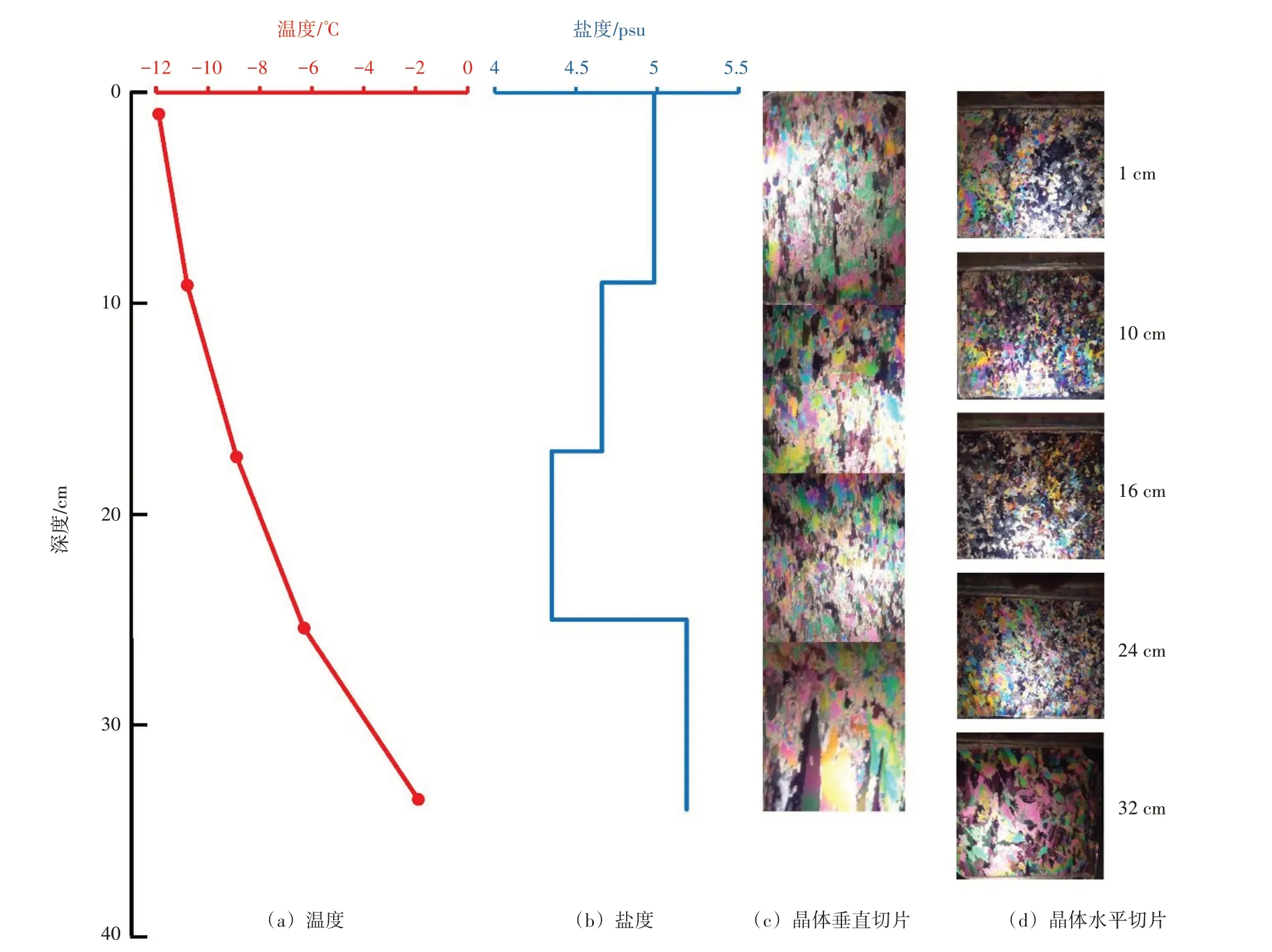
图2 海冰现场温度和盐度垂直剖面及垂直、水平冰晶体切片

整个冰层上部为厚约29 cm 的粒状冰，下部为厚约5 cm 的柱状冰，粒状冰层的粒径沿厚度无明显变化。以往文献报道，渤海海冰主要为柱状结构[11,15]。图2（c）所示的冰层以粒状结构为主意味着冰层可能在生长早期经历了长期湍动的状态[24]。在结冰的初始阶段，水面上的冰针相互联结形成脂状冰，并随着气温的降低而不断变厚形成板冰。全球变暖延长了脂状冰形成板冰的时间[20]。在风、波浪和海流的作用下，脂状冰经历反复的冻结-破碎-再冻结的过程，直到形成板冰。从脂状冰到形成板冰经历的时间越长，冰层的晶体结构越趋向于粒状。之前的试验广泛研究了柱状海冰而非粒状海冰的弯曲强度和有效弹性模量。在全球变暖的情况下，渤海粒状冰在整个冰层中的比例增加，这就需要更好地了解粒状冰的弯曲力学特性。

2 海冰弯曲试验方法

本文采用实验室三点弯曲试验测试冰试样的弯曲强度和有效弹性模量。根据图2（c）垂直切片观察到的粒状-柱状冰层界面，用电链锯将冰坯分开。在切除顶部约3 cm 厚的含有少量泥沙等杂质的疏松薄层后，对剩余粒状冰坯从上到下分三层进行切割。最终，加工成65 cm×7 cm×7 cm的长方体试样，其长轴平行于原始冰层表面。本文设计以垂直于初始冰层表面方向作为加载方向，故加工时对冰试样垂直于冰生长方向的表面进行标记。本文共制备三点弯曲冰试样42 块。依据渤海辽东湾以往测得和现场测得的海冰温度范围，设计在-15 ℃、-10 ℃和-5 ℃三个试验温度下进行弯曲试验[15]。在进行试验之前，将每个冰试样放入塑料袋中防止升华，并分别在各自试验温度下储存于恒温箱中至少24 h。

海冰三点弯曲试验使用大连理工大学研制的多功能冰力学试验机[25]（图3）。力学传感器固定在试验机液压泵施力端，量程为10 kN，线性度（又称非线性误差，是传感器校准曲线与拟合直线间的最大偏差ΔYmax与满量程输出Y的百分比）为0.20%。激光位移传感器用于测量加载端位移，量程为25 mm，线性度为0.05%。采用变频器控制加载端位移速率。根据Han 等[26]给出的方法估算冰梁跨中底部的应变和应变速率：

图3 多功能冰力学试验机

式中：ε为冰梁跨中底部的应变；ε̇为冰梁跨中底部的应变速率（/s）；h为冰试样的高（mm）；L为简支梁支点间距，本文为595 mm；δ为冰梁跨中处的位移（mm）；δ̇为冰梁跨中处的位移速率（mm/s）。本文弯曲试验的应变速率范围为1×10-6～6×10-4/s。通过以太网数据采集程序同步采集试验力学信号和位移信号，试验数据采集频率设为400 Hz，即力信号与位移信号每秒各采样200个数据。弯曲试验期间冰试样发生断裂时，试验立即终止，并记录数据。

根据线弹性梁理论计算冰试样的弯曲强度和有效弹性模量：

式中：σf为弯曲强度（MPa）；Ef为有效弹性模量（GPa）；Pmax为峰值力（N）；w为冰试样的宽（mm）；δmax为达到峰值力时冰梁跨中处的位移（mm）。

在进行弯曲试验前，分别以±0.01 g 精度的电子天平和±1 mm 精度的钢尺测量每个冰试样的重量和尺寸，以通过质量体积法计算冰试样的密度。每次弯曲试验结束后，收集断裂后的冰试样碎块并放入塑料袋中，在室温下融化。样品完全融化后，用精度为±0.01 psu 的盐度计测量盐度。由于弯曲试验只经历很短的时间，因此冰试样内卤水的排泄在试验期间很少发生。孔隙率是卤水体积和气体体积的总和，综合了海冰温度、盐度和密度的影响，这一性质对评价海冰的物理特性具有重要意义。使用冰试样的温度、盐度和密度数据，并根据Cox 等基于标准海冰的相平衡表格建立的方程[27]，确定冰试样的卤水体积、气体体积和孔隙率。用于计算-22.9～-2 ℃的卤水体积、气体体积和孔隙率的方程如下：

式中：vT为孔隙率（体积分数），va为气体体积（分数），vb为卤水体积（分数），Ti为冰试样温度（℃），Si为冰试样盐度（psu），ρ为冰试样密度（g/cm3），ρi为纯冰密度（g/cm3），F1（Ti）和F2（Ti）为关于Ti的三次多项式，其系数由表1给出。

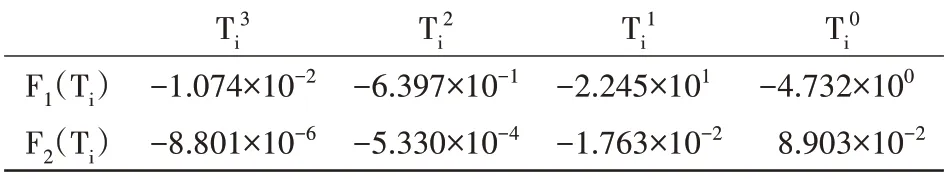
表1 F1（Ti）和F2（Ti）的多项式系数

3 结果分析与讨论

3.1 海冰弯曲力学特性与物理指标的关系

3.1.1 弯曲强度

本文首先对弯曲强度与卤水体积之间的关系进行了分析。图4 显示了弯曲强度与卤水体积分数平方根的关系。数据点整体分布较为离散，冰试样的弯曲强度随卤水体积的变化趋势不明显。参考以往大多数研究中给出的海冰弯曲强度与卤水体积的关系，对弯曲强度与卤水体积平方根之间的关系使用负指数函数进行回归分析，结果表明其在显著性水平p=0.1 时不显著（图4）。使用其他常见函数（线性、幂函数等）对数据点进行回归分析，得到的结果依旧不显著。

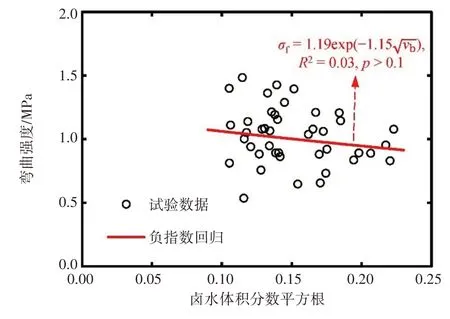
图4 粒状海冰试样弯曲强度与卤水体积平方根的关系

通常，小尺寸冰试样测得的冰强度具有广泛的离散性。这可能是由于天然冰的不均匀性以及冰层内存在缺陷造成的。再者，渤海海冰温度高的特征以及采样、运输和储存期间冰试样的卤水泄漏降低了卤水体积分数在孔隙率中的占比[28]。此外，本文中冰试样卤水体积分数平方根在0.10～0.22 的狭窄范围内，使得弯曲强度对卤水体积分数的变化不敏感。因此，根据上述结果直接得出海冰弯曲强度与卤水体积无关的结论是草率的。但至少可以推断，对于本文的渤海三点弯曲冰试样使用卤水体积作为典型物理指标来表征弯曲强度变化可能并不合适。

本试验的冰试样中平均气体体积（35.94‰±19.45‰）明 显 大 于 平 均 卤 水 体 积（23.84‰±10.46‰）。在海冰中，卤水胞和气泡都不具备承受荷载的能力。因此，在分析影响海冰力学性能的物理因素时，应考虑气泡的影响，尤其是对实验室相对较高试验温度下测试的小尺寸冰试样。然而，很少有研究者定量分析孔隙率对海冰弯曲强度的影响。李志军等[16]通过对多年收集到的渤海海冰试样在严格控温和精确测量冰密度后进行实验室三点弯曲试验，得到了渤海平整冰（柱状冰）三点弯曲峰值强度与孔隙率间的幂函数关系：

式中：σf单位为MPa，vT单位为‰，可决系数R2=0.64。图5 显示了本试验得到的粒状冰试样弯曲强度与孔隙率的关系。可以看出，冰试样的弯曲强度随孔隙率的增大有明显的降低趋势。参考公式（9）的形式，对本试验得到的冰试样弯曲强度与孔隙率的关系使用幂函数进行回归分析，得到如下结果：

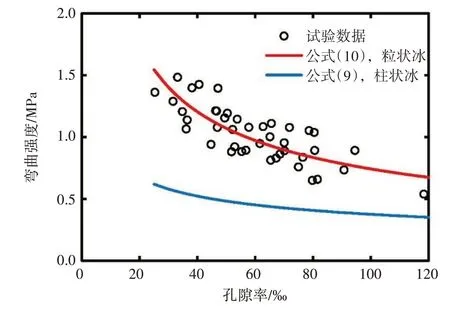
图5 海冰弯曲强度与孔隙率的关系

式中：σf单位为MPa，vT单位为‰。上式的可决系数R2=0.62，显著性水平p＜0.01。与图4 中的结果比较可见，孔隙率比卤水体积更适合用作估算渤海粒状海冰弯曲强度的综合物理评价指标。

图5中红线为本文得到的渤海粒状海冰弯曲强度与孔隙率的关系曲线（公式（10）），蓝线为李志军等[16]给出的渤海平整冰（柱状冰）三点弯曲峰值强度与孔隙率间的关系曲线（公式（9））。将两者比较可发现，无论是渤海的柱状冰还是粒状冰，弯曲强度随孔隙率增大而降低的趋势是一致的。在相同孔隙率下，渤海粒状冰的三点弯曲强度明显高于柱状冰，这与以往一些研究中观察到的现象一致[22-23]。Timco 等[22]报道，尽管粒状冰层的盐度较高，但整个冰层上部粒状冰的弯曲强度仍高于下部柱状冰的弯曲强度。Blanchet等[23]将粒状海冰较高的弯曲强度归因于比柱状海冰更小的粒径。此前，Tabata[29]通过弯曲时粒状海冰和柱状海冰之间破坏线上孔隙线密度的差异解释了这一现象。因此，在受冰灾害影响的海域，结构物上同一孔隙率下相同厚度的粒状冰层可能比柱状冰层产生更多的弯曲冰荷载，这应在结构物的抗冰设计中予以考虑。

3.1.2 有效弹性模量

海冰的黏弹塑性导致有效弹性模量的测量值表现出较强离散性，尤其是对于采用力学试验进行的测量[10]。为了厘清有效弹性模量和孔隙率之间的关系，将5‰的孔隙率作为一个区间单元，在每个区间单元内对试验数据的孔隙率和有效弹性模量进行平均。图6（a）显示了平均处理后粒状海冰试样有效弹性模量与孔隙率的关系。粒状海冰试样的有效弹性模量随孔隙率的增大有明显的减小趋势。同样使用幂函数关系表征有效弹性模量与孔隙率的关系，得到如下结果：

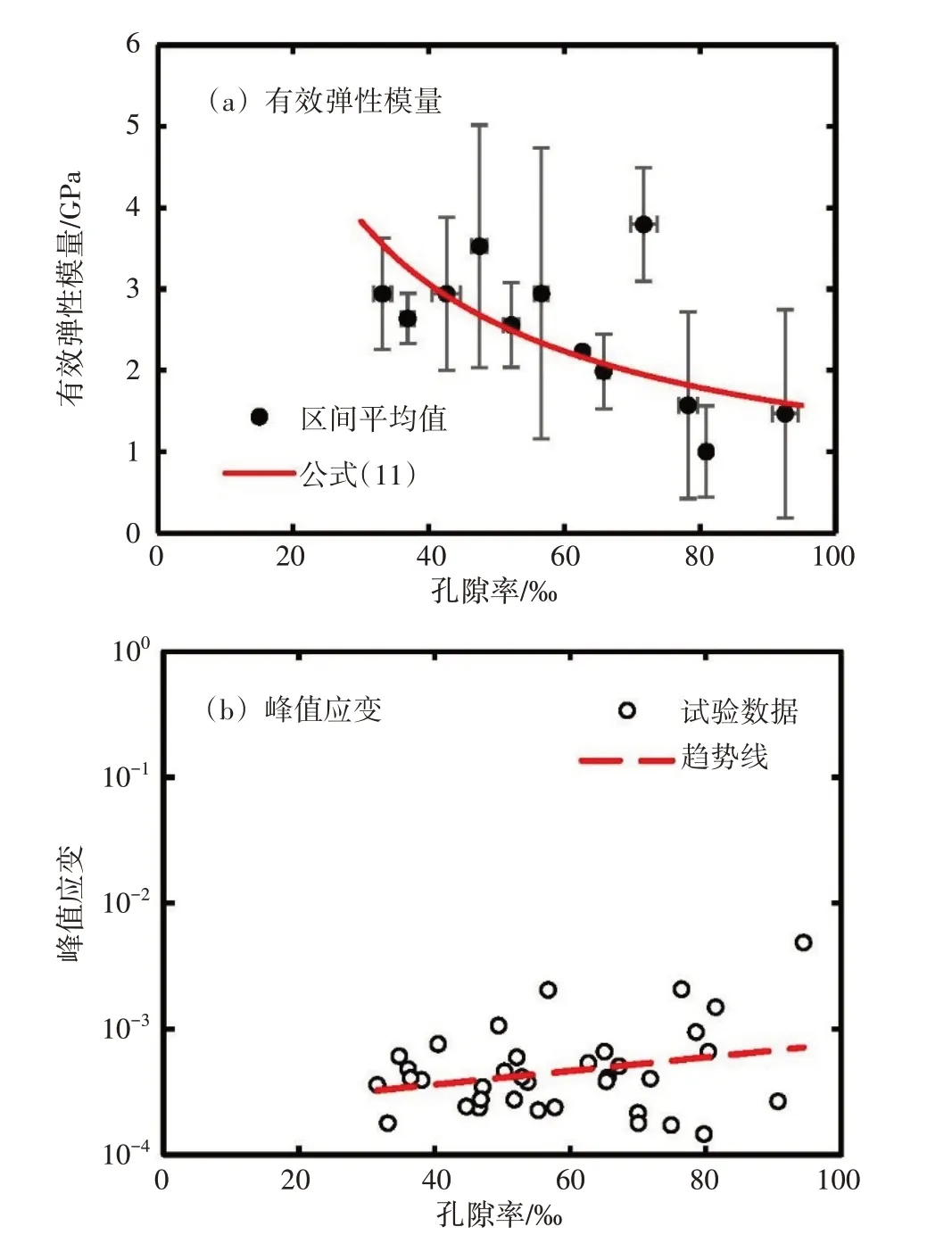
图6 粒状海冰试样有效弹性模量和峰值应变同孔隙率的关系

式中：Ef单位为GPa，vT单位为‰。上式可决系数R2= 0.41，显著性水平p＜ 0.01。

以往研究对有效弹性模量随着卤水体积或孔隙率的增加而降低的观点较为一致[8,10]。图6（b）显示粒状海冰试样峰值应变（达到峰值力Pmax时冰梁跨中底部的应变）随孔隙率的增大有增大的趋势。海冰中卤水胞和气泡的增多会降低固体冰含量，使海冰更具有黏性和延性，在相同荷载下会产生更多延迟弹性和非弹性变形。此外，海冰的弯曲强度随着孔隙率的增加而降低。因为有效弹性模量是峰值应力与峰值应变的比值，所以有效弹性模量随着孔隙率的增加而降低。

3.2 海冰弯曲力学特性与应变速率的关系

3.2.1 弯曲强度

孔隙率对海冰的弯曲强度影响显著（图5）。为了厘清应变速率对粒状海冰弯曲强度的影响，需要首先排除孔隙率对弯曲强度的影响。参考Aly等[30]给出的归一化方法，使用下式将弯曲强度归一化到同一参考孔隙率下：

式中：σn是归一化后的弯曲强度，σm是使用实测孔隙率代入公式（10）获得的弯曲强度，σr是使用参考孔隙率代入公式（10）获得的弯曲强度。公式（12）实际上是将不同孔隙率下的弯曲强度转换为相同孔隙率下的弯曲强度，这就相当于将孔隙率对弯曲强度的影响进行排除。本文选择平均孔隙率59.79‰作为参考孔隙率，以此确定的σr= 0.97 MPa。

图7 显示了粒状海冰试样的归一化弯曲强度与应变速率的关系。归一化强度值介于0.76～1.23 MPa 的范围内，在整个应变速率范围内几乎不依赖于应变速率变化。因此，在1×10-6～6×10-4/s的应变速率范围内，应变速率对粒状海冰试样的弯曲强度没有显著影响。

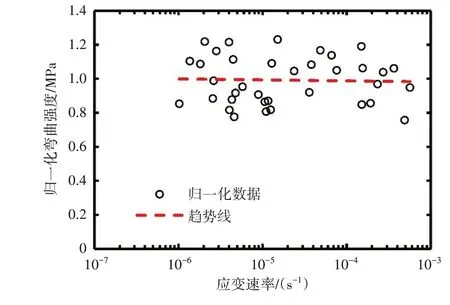
图7 粒状海冰试样归一化弯曲强度与应变速率的关系

应变速率似乎并不会影响海冰的弯曲强度。海冰的弯曲破坏本质上是拉伸破坏，因为海冰是一种压缩强度远大于拉伸强度的材料，拉伸应力控制海冰的弯曲破坏。而海冰的拉伸强度与应变速率无显著关系[10,31]，这与本文得到的应变速率对弯曲强度无显著影响的现象一致。

3.2.2 有效弹性模量

为了厘清应变速率对粒状海冰有效弹性模量的影响，仍使用公式（12）的归一化方法对海冰试样的有效弹性模量数据进行归一化处理，以排除孔隙率对有效弹性模量的影响。公式（11）用于计算相关的有效弹性模量值，仍以平均孔隙率59.79‰作为参考孔隙率，以此确定的Er= 2.21 GPa。图8（a）显示了归一化有效弹性模量与应变速率的关系。归一化值随应变速率的增大而增大，表明粒状海冰试样的有效弹性模量随应变速率的增大而增大。

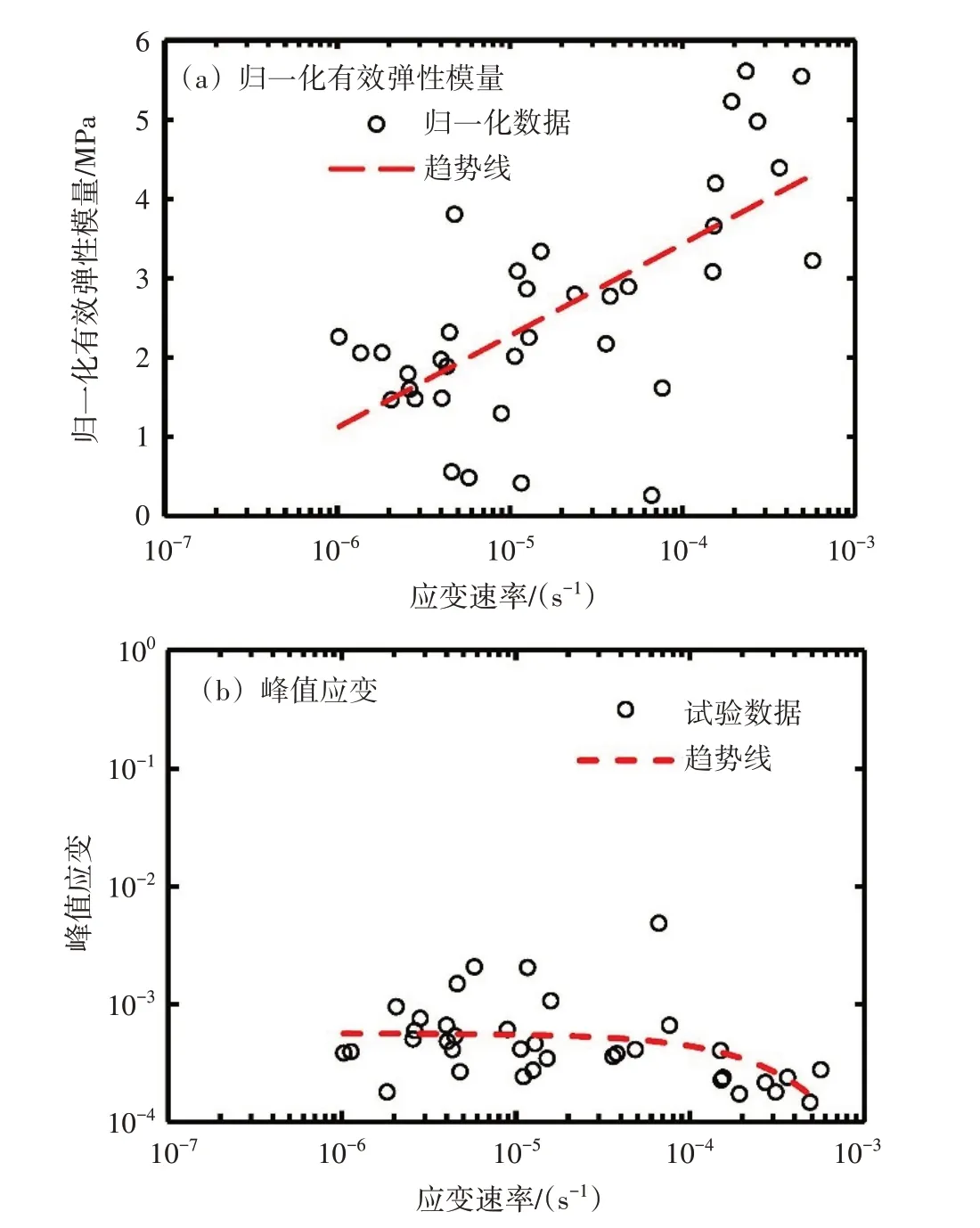
图8 粒状海冰试样归一化有效弹性模量和峰值应变同应变速率的关系

图8（b）显示粒状海冰试样的峰值应变随应变速率的增大呈减小趋势，这是因为海冰的非弹性应变和延迟弹性应变随着应变速率的增加而减小[10,32]。此外，弯曲强度与应变速率无显著关系（图7）。因为有效弹性模量是峰值应力与最大应变的比值，所以有效弹性模量随着应变速率的增大而增大。

根据以上结果，进一步研究孔隙率和应变速率对海冰有效弹性模量的耦合影响。有效弹性模量作为孔隙率和应变速率的双参数方程表示形式如下：

通过最小二乘法拟合弯曲试验数据可得a=206.25，b= -0.61，c= 0.18，可决系数R2= 0.51，显著性水平p＜ 0.01。图9（a）、（b）分别显示了表征有效弹性模量与孔隙率和应变速率关系的三维拟合曲面和等值线图。

3.3 试验结果与其他研究结果的对比

为分析本文三点弯曲试验获取的海冰弯曲强度的有效性，将本文试验结果与其他弯曲试验结果进行了对比。由于目前国内外尚未有针对粒状海冰的弯曲强度进行相关研究，且极少研究使用孔隙率表征海冰弯曲强度，因此仅将本文与其他研究的海冰弯曲强度与卤水体积关系进行对比。国际油气行业规范ISO 19906[33]推荐使用Timco等[14]提出的公式估算海冰弯曲强度，如下式：

该式是基于全球众多覆冰海域的939 次冰梁试验（悬臂梁+简支梁试验）结果获得的，并未区分海冰的晶体类型。此外，孟丁丁等[13]于2020－2021 年冬季在辽东湾东岸采集海冰试样进行了三点弯曲试验，该试验未指明海冰的晶体类型。

将本文结果与以上两文献中的结果绘制于图10（a）中进行对比。各研究的结果均显示弯曲强度随卤水体积平方根的增大呈降低趋势。本文所获得的数据点主要分布于文献[33]推荐的关系曲线上方。对于同样取自辽东湾东岸的海冰，在卤水体积平方根小于0.13时本文的弯曲强度与文献[13]的结果接近，而在卤水体积平方根大于0.13 时本文的弯曲强度大于文献[13]的结果。以往的研究结果表明试验类型（悬臂梁、三点或四点弯曲试验）、试样尺寸、加载方向和应变速率对海冰弯曲强度没有显著影响[10,14]。因此，导致不同研究强度值差异的主要因素应是海冰的物理性质以及微观结构。本文所使用的试样全部为粒状冰，其晶体粒径显著小于柱状冰，且弯曲破坏时粒状海冰在破坏平面上孔隙（卤水胞和气泡）的线密度小于相同孔隙率的柱状海冰，这是本文弯曲强度较高的主要原因[23,29]。当卤水体积平方根小于0.13 时，文献[13]的试样温度为-35～-15 ℃，显著低于本文的试样温度。这使得文献[13]中这部分试样弯曲强度相对偏高，从而在数值上接近本文结果。

图10 不同研究结果的对比

ISO 19906[33]推荐使用下式估算海冰的弹性模量：

式中：E为海冰弹性模量，单位为GPa；E0为淡水冰弹性模量，取值9～10 GPa。将本文结果与公式（15）的曲线（E0取9 GPa）绘制于图10（b）中进行对比。（有效）弹性模量均随孔隙率的增大而减小。文献[33]推荐的关系曲线接近但略高于本文结果，这主要是海冰的弹性模量与有效弹性模量之间的差异造成的。本文通过三点弯曲试验获得了海冰的有效弹性模量。海冰作为一种多相复合的黏弹塑性材料，其在有限时间的外力作用下发生变形时，除弹性变形外会不可避免地伴随着延迟弹性和塑性变形[10]。因此，使用力学方法获取的有效弹性模量总是小于海冰真正的弹性模量。然而，海冰的有效弹性模量更适用于大多数实际工程问题，如冰盖的承载力以及结构物上的冰力的计算。

4 结论

为了理解渤海粒状海冰的弯曲力学特性，在2010－2011 年冬季于辽东湾现场采集冰坯，进行了实验室粒状海冰的三点弯曲试验以及物理特性测量，分析了孔隙率和应变速率对粒状海冰弯曲强度和有效弹性模量的影响。相较于卤水体积，孔隙率更适合表征粒状海冰的弯曲力学特性。粒状海冰弯曲强度与孔隙率呈负幂函数关系，而与应变速率无显著关系。粒状海冰有效弹性模量与孔隙率呈负幂函数关系，且随应变速率增大而增大。在此基础上对粒状海冰有效弹性模量关于孔隙率、应变速率进行双因素分析，拟合得到了粒状海冰有效弹性模量关于孔隙率、应变速率的双参数表达式。本文结果可为推算不同条件下粒状海冰弯曲强度和有效弹性模量的设计参数提供参考依据。

在全球变暖影响下，渤海海冰的性质发生了一些变化，冰盖中的粒状冰厚度有增大的趋势。尽管本研究试验数据的时间较久且海冰样本的数量较少，但目前关于粒状海冰弯曲强度和有效弹性模量的研究很少，本文的研究结果是对渤海海冰力学特性的有益补充。在后续的研究中我们将继续积累渤海粒状海冰弯曲力学特性的相关试验数据。