浅层顺层滑坡成灾机制分析及其稳定性评价

朱 涛, 翟亚锋, 翟会君

(河南省地质矿产勘查开发局第四地质勘查院,河南 郑州 450000)

0 引言

浅层顺层滑坡在我国广泛分布。按《GB/T 32864—2016滑坡防治工程勘查规范》[1]规定,浅层滑坡定义为滑体厚度小于10 m。此类滑坡规模一般较小,但其自稳能力相对也较弱,易出现局部变形破坏,若区内居民较多,其潜在危害显著,且该类滑坡易引发水土流失,不利于环境保护。因此,该文将浅层顺层滑坡作为研究对象,重点开展其成灾机制分析及稳定性评价[2-3]。目前,许多学者利用数值模拟、数理统计等手段,从浅层滑坡影响因素出发,研究了降雨、植被等对浅层滑坡稳定性的影响规律,并探究了此类滑坡的演化机制[4-7]。

上述研究表明: 一方面,开展浅层滑坡研究具有重要意义,即其能为此类滑坡灾害防治提供具有针对性的理论基础; 另一方面,浅层滑坡发育存在一定的区域性特征,即不同地区的浅层滑坡具有相应差异。因此,仍有必要针对具体实例开展进一步研究。浅层滑坡影响因素与一般滑坡的影响因素相对较为一致,但也具一定的特征性。因此,本文提出基于浅层滑坡所处地质条件,开展其成因机制分析。同时,以往滑坡稳定性评价多侧重于现状评价,缺乏稳定性预测评价,分析结果的全面性受限,因此,本文提出将滑坡稳定性评价过程划分为两步,即稳定性现状评价和预测评价,并通过传递系数法实现其稳定性现状评价,再通过变形预测实现其稳定性预测评价。研究旨在有效掌握浅层顺层滑坡的成灾机制,并为其稳定性评价提供一种思路,从而奠定灾害防治的理论基础。

1 基本原理

1.1 稳定性现状评价模型的构建

据工程实际,滑坡常用的现状稳定评价模型主要是传递系数法,其原理已在《GB/T 32864—2016滑坡防治工程勘查规范》[1]中详述,因此,不再赘述[8-9]。

(1)计算工况。在滑坡稳定性现状评价过程中,共设置了3种工况: 工况1,天然工况,该工况是评价滑坡天然状态下的稳定性; 工况2,暴雨工况,该工况是评价滑坡暴雨状态下的稳定性; 工况3,地震工况,该工况是评价滑坡地震状态下的稳定性。

(2)计算参数。据滑坡勘查成果,其稳定性计算参数见表1。

表1 不同工况条件计算参数Tab.1 Calculation parameters under different conditions

(3)稳定性状态划分。据《GB/T 32864—2016滑坡防治工程勘查规范》[1],以稳定性系数Fs为基础,开展滑坡稳定性状态划分。若Fs属小于0时,滑坡处于不稳定状态; 若Fs属[0,1.05)区间时,滑坡处于欠稳定状态; 若Fs属[1.05,1.15)区间时,滑坡处于基本稳定状态; 若Fs属大于等于 1.15 时,滑坡处于稳定状态。

1.2 稳定性预测评价模型的构建

一般来说,滑坡变形越大,其稳定性相对应越弱,因此,提出利用变形预测来开展滑坡稳定性预测评价。灰色模型(简称GM(1,1)模型)能在部分信息未知情况下实现非线性预测,使得其在变形预测领域取得了广泛应用,提出利用其构建滑坡变形预测模型,但传统GM(1,1)模型多具离散形式,而滑坡变形具有连续形式。为解决该问题,袁德宝等[10]将分数阶算子引入其中,构建出了分数阶算子条件下的灰色模型(简称EGM(1,1)模型),且考虑到分数阶算子是由使用者确定,为保证其最优性,提出利用改进粒子群算法(improve particle swarm optimization,IPSO)[11]开展其优化处理。该方法是粒子群算法的改进型,结合其基本原理,其寻优过程有4步。

(1)开展粒子种群的初始信息设置,如将学习因子设定为1和2,权重因子设定为0.7,种群规模设定为600。

(2)将各粒子的当前位置设置为分数阶算子,并以其预测结果的平均绝对百分误差为基础,初步确定出群体的最佳粒子位置。

(3)更新每个粒子的位置和速度,并重新计算每个粒子更新后的平均绝对百分误差值,将其与最佳粒子的平均绝对百分误差值对比,若前者更优,则将最佳粒子位置进行重新设置,反之,保留原位置。

(4)当完成寻优后,将全局最佳粒子对应的分数阶算子输出,即可完成其寻优过程。

虽然利用IPSO算法保证了EGM(1,1)模型分数阶算子的最优性,但限于滑坡变形的非线性特征,其预测结果还是会存在一定误差,即IPSO-EGM(1,1)模型的预测结果仍会存在预测误差。为充分保证预测精度,再提出利用混沌理论开展其误差弱化处理[12-13]。结合其基本原理,将其预测步骤说明如下。

先利用Lyapunov指数法开展待预测误差序列的混沌特征识别,按照其识别流程,计算判别参数λ,其计算公式为

(1)

式中:tM、t0为时间变量,s;M为迭代次数,次;Li为原始距离值;li为重构后的距离值。

以λ值开展误差序列的混沌特征识别,即: 若λmax值大于0,那么预测误差序列具混沌特征; 反之,则不具混沌特性。

利用延迟时间算法确定嵌入维数,并利用去偏复自相关法确定延迟时间,通过此两参数可实现误差序列的相空间重构。同时,再利用Lyapunov指数法开展误差序列的预测处理,具体过程为: 将ψi作为预测中心,计算与其最近相邻点间的距离d。公式为

(2)

式中:ψi、ψj为相空间节点。

若d值最小,即可反推出预测误差的预测值。

据上,最终将滑坡变形预测模型确定为IPSO-EGM(1,1)-WT模型。

基于预测结果,先引入两个速率统计量,即V1速率(mm/周)和V2速率(mm/周),前者是实测数据最后4期的变形速率均值,后者是4期外推预测结果的变形速率均值。若V1速率相对更大,说明滑坡变形趋于收敛,其后续稳定性亦趋于稳定; 反之,说明滑坡变形趋于继续增加,其后续稳定性亦趋于不稳定。

2 实例分析

2.1 工程概况

某滑坡位于斜坡前缘地段,平面具扇形形态(图1),所处斜坡坡度为20°～40°,植被较发育。据现场调查,滑坡主滑方向为30°,纵向长约 150 m,宽度间于90～180 m。土层厚度具有一定差异,主要间于3.2～6.1 m,平均厚度约4.5 m,总体积约8.4×104m3,属典型的浅层滑坡。

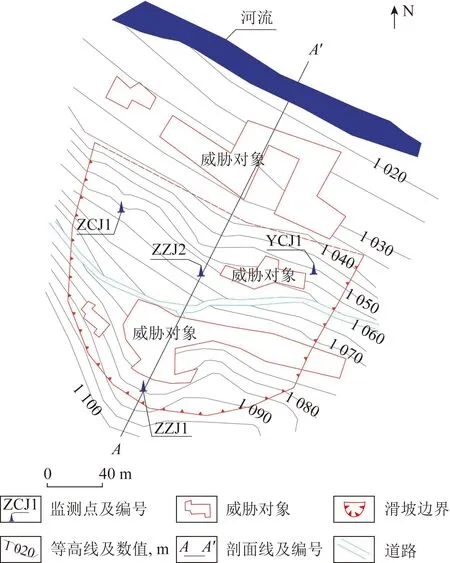
图1 滑坡平面形态Fig.1 Plane modality of landslide

据钻探成果,将滑坡结构地层特性阐述如下。

(1)滑体土。岩性主要是填土和粉质黏土: 前者主要分布于滑坡中上部,仅局部分布,对滑坡影响有限; 后者在滑坡区广泛分布,紫红色,多呈可塑-硬塑状,局部含有少了角砾,母岩成分多是泥岩,磨圆度较差。

(2)滑带。岩性主要是黏土,紫红色,属泥岩风化后的产物,整体力学性质较差,遇水易软化,多呈可塑状。

(3)滑床。岩性为泥岩,紫红色,节理裂隙较发育,岩体整体完整性相对较差,强度中等,岩层产状为46°∠34°,结合滑坡主滑方向,该滑坡具有顺层滑坡特征。

将主滑面(即图1中A-A′剖面)的地层结构阐述如图2所示。

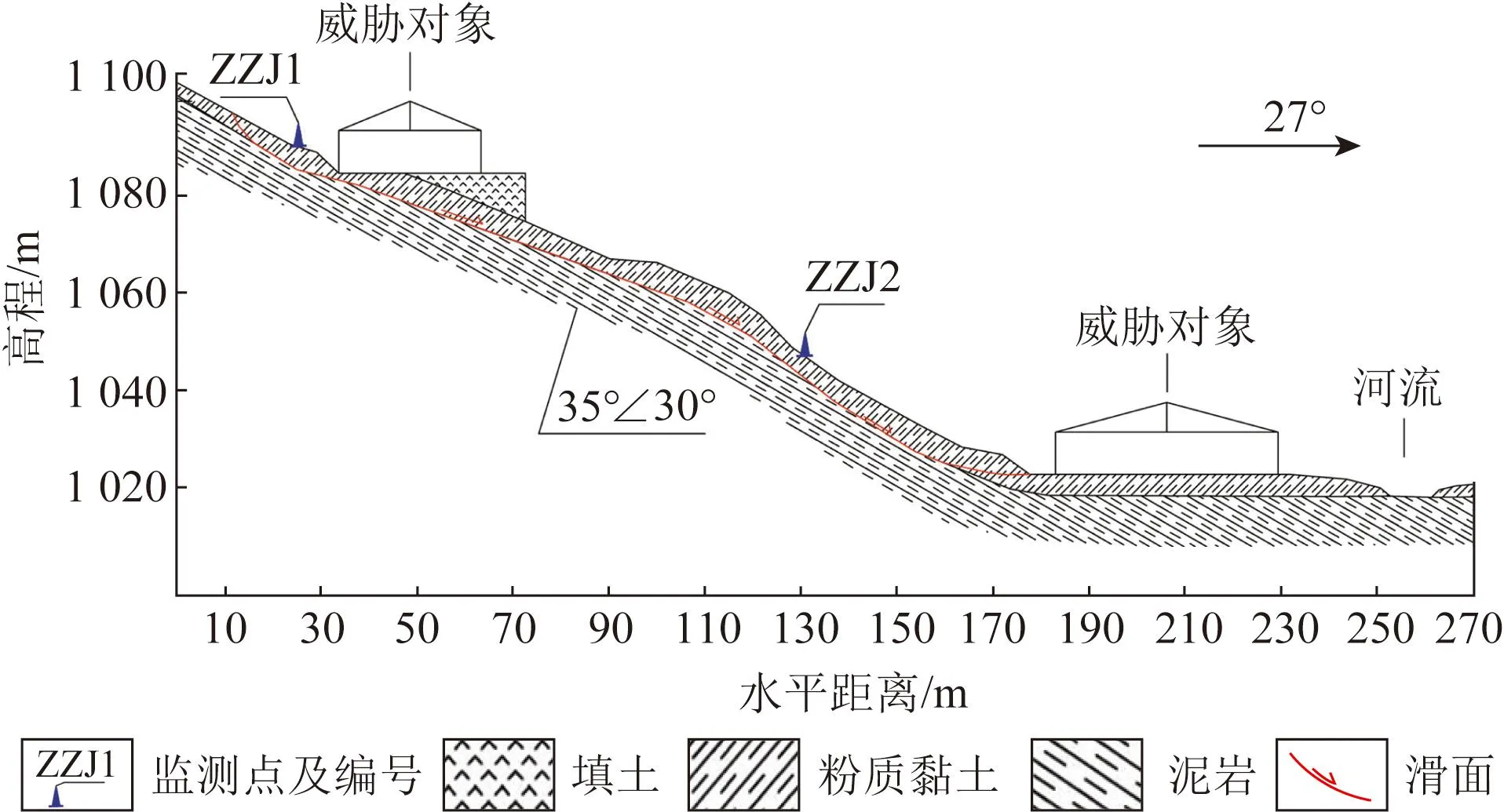
图2 滑坡地层结构A-A′剖面图Fig.2 A-A′ profile of landslide stratum structure

该滑坡早在2010年雨季就开始出现变形情况,其后每年变形均有所发育,主要表现为局部房屋倒塌及裂缝发育,其中,裂缝多会后期自动愈合。据上,该滑坡变形特征显著,且区内威胁居民相对较多,因此,开展本研究十分必要。

为定量掌握滑坡变形量,在滑坡上共计布置了4个监测点,用于开展监测位置的总位移监测,其中,主轴上布置了2个,左右两侧分别布置1个,具体位置见图1。据统计,共计得到40期(监测周期为2 d,监测时段为2022年7月8日至2022年9月26)的滑坡变形数据,其变化曲线如图3所示。

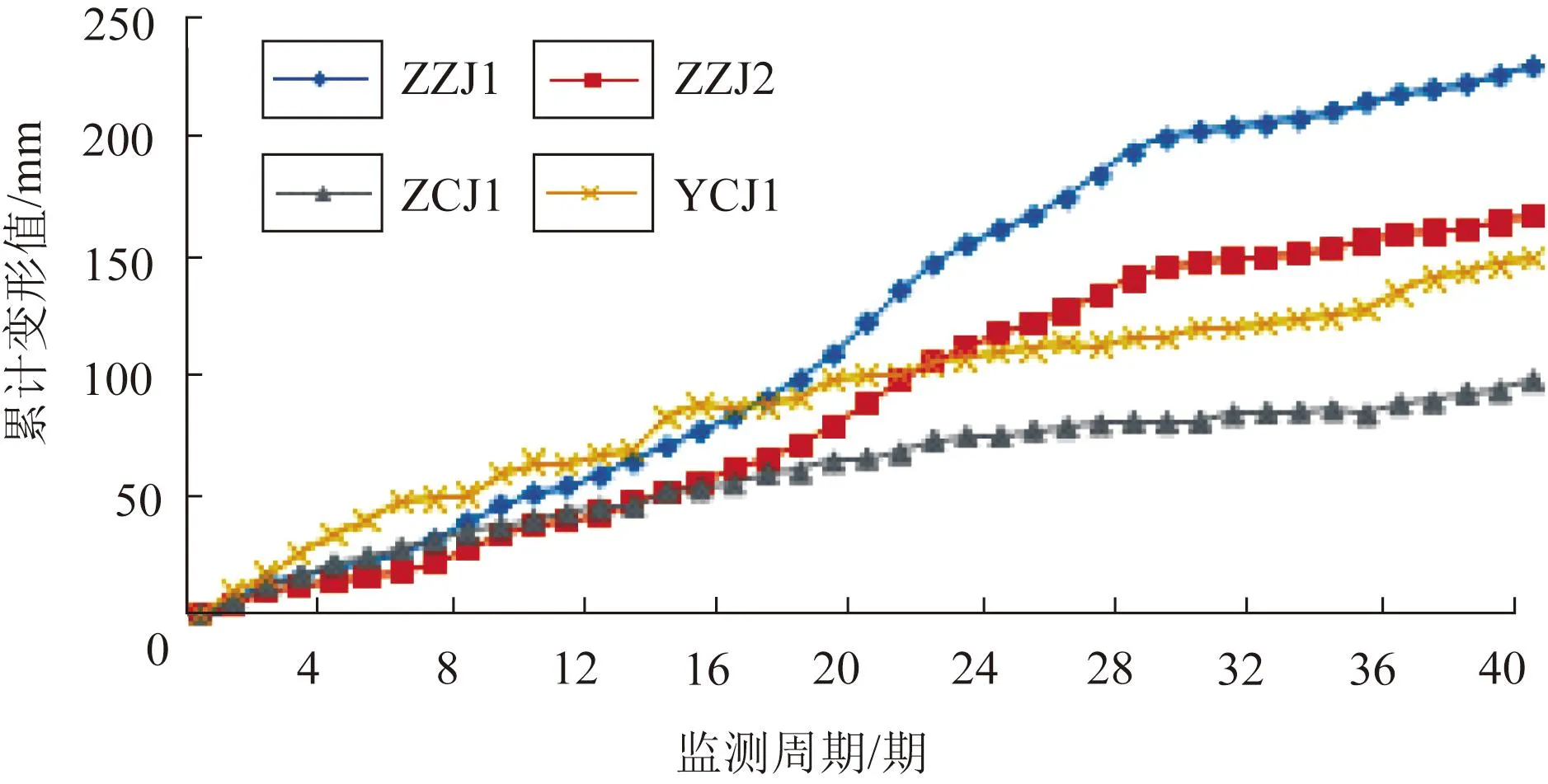
图3 滑坡累计变形曲线Fig.3 Cumulative deformation curves of landslide

据图3,滑坡各位置处的累计变形总体呈持续增加趋势,只是局部短时存在负增长。ZZJ1监测点的累计变形量为229.03 mm,相对最大,说明后缘相对更不稳定; ZZJ2监测点的累计变形量为166.98 mm; 两者均位于滑坡主轴上,充分说明主轴是滑坡稳定性相对最弱位置,侧面也验证了后续通过主轴开展滑坡稳定性现状评价的可行性。在滑坡两侧,西北侧ZCJ1监测点的累计变形量为97.63 mm,东北侧YCJ1监测点的累计变形量为148.33 mm,对比而言,滑坡右侧变形相对更大。

2.2 滑坡成灾机制分析

2.2.1 滑坡影响因素分析

一般来说,浅层滑坡变形影响因素相对较多,其主要可从物源条件、地形条件及水源条件等方面开展分析,具体分析如下。

(1)土层厚度因素。土层较薄是浅层滑坡的特有特征。一方面,土层薄,利于降雨软化,促使滑坡易出现变形破坏,且该类变形无统一规律性; 另一方面,土层厚度对滑坡破坏形式具有一定影响,若土层相对较薄,更易出现滑移破坏,若土层相对较厚,更易出现蠕滑破坏。

(2)地形条件因素。地形条件对浅层滑坡的影响较大,又可进一步细分为坡度因素、地形因素及高差因素。①坡度因素。坡度是滑坡灾害的重要成因,一般来说,斜坡坡度越陡,其越容易发生失稳破坏。结合调查成果,在坡度间于20°～40°时,浅层滑坡更易发育。②地形因素。地形对浅层滑坡的影响规律主要表现为: 地形为凸形时,浅层滑坡相对最易发育; 地形为直线形时,浅层滑坡发育一般; 地形为凹形时,浅层滑坡一般不发育。③高差因素。由于浅层滑坡滑体厚度较薄,其固有稳定属性相对就较差,因此,该类滑坡难以形成较大的高差。滑坡发育的主要高差范围是20～50 m,其次是50～100 m,其余高差范围的滑坡发育相对较少。

(3)地层岩性因素。地层岩性与浅层滑坡的形成具有密切关系,一般来说,浅层滑坡发育区的地层力学参数均较低,即软质岩更易形成浅层滑坡,其次是软硬相间岩,而硬质岩不易形成浅层滑坡。

(4)地质构造因素。一方面,地质构造是形成滑坡区的原始地形地貌,是浅层滑坡形成的基础; 另一方面,地质构造会极大程度上影响滑坡地层的完整性,对区内节理系统的发育也有一定的影响,进而影响滑坡稳定性。

(5)植被与土地利用因素。该因素主要包含植被覆盖因素和土地利用类型因素。①植被覆盖因素。一般来说,植被对土体具有一定的加固作用,主要表现为: 植物根系深入土层中,一定程度上抑制了土体裂隙的发育,可有效减少坡面破坏。由于浅层滑坡滑体厚度本身较薄,此因素对其影响显著,从植被极疏至中等再至茂密,浅层滑坡的发育频率越来越少,尤其在植被茂密时,几乎无浅层滑坡发育。②土地利用类型因素。由于土地利用类型不同,其对应植被覆盖情况及其种类均随之不同,这也会一定程度上影响土体对雨水的吸收情况。据调查,旱地、灌木类型具较高浅层滑坡发育率,其余类型的发育率相对较低。

(6)降雨因素。降雨一直以来就是滑坡失稳破坏的重要诱因,其对浅层滑坡尤为明显,主要是因为浅层滑坡滑体较薄,雨水入渗路径较短,即使小雨也可能造成局部失稳,其影响规律可总结为: 一方面,雨水入渗不仅会增加滑体重度,还会减弱滑面抗剪强度,降低滑坡稳定性; 另一方面,若存在短时强降雨,易在地表形成径流,造成坡面冲刷等,这对浅层滑坡稳定极为不利。

(7)人类工程活动因素。一般来说,存在滑坡灾害的范围均会具有一定程度的人类工程活动,其对滑坡的影响主要表现为: 工程活动造成削坡、减载等,打破了原有坡体的内力平衡,诱使滑坡灾害发生,尤其对于浅层滑坡,轻微的扰动极可能诱发局部变形。

据上,浅层滑坡的影响因素相对较多,且其对各类因素的敏感性均较强,这是因为其滑体厚度较薄,受外界扰动影响较大。

2.2.2 滑坡形成机制分析

结合上述滑坡影响因素分析及工程实例概况,将该文实例滑坡的形成机制总结如下。

(1)滑坡所处斜坡坡度为20～40°,且具顺向坡的坡体结构,为滑坡灾害形成奠定了基础。

(2)滑坡区基岩为泥岩,本身遇水易软化,易形成软弱潜在滑面,其形成机理为: 滑体较薄,雨水易入渗,且当渗至基覆界面时,下覆泥岩又具一定隔水性,进而雨水在基覆界面汇集; 同时,降雨停止后,基覆界面处的水分蒸发也是相对最晚蒸发,如此长期作用,就会形成基覆滑面。

在各类影响因素综合作用影响下,尤其是在降雨、人类工程活动长期诱发作用条件下,滑坡易出现局部变形,存在整体失稳风险。

2.3 滑坡稳定性评价

2.3.1 稳定性现状评价

据1.1节思路,通过传递系数法开展滑坡主滑面(即A-A′剖面)的稳定性分析,其计算结果如表2所示。工况1属稳定状态; 工况2属欠稳定状态; 工况3属基本稳定状态。通过上述,在稳定性现状条件下,得出该滑坡在天然状态下仍处于稳定状态,但在不利工况条件下,存在失稳风险。

表2 A-A′剖面稳定性计算结果Tab.2 Stability calculation results of A-A′ profile

2.3.2 稳定性预测评价

该节重点按照1.2节思路,通过IPSO-EGM(1,1)-WT模型开展滑坡稳定性预测评价。在该过程中,将前35期数据作为训练集,后5期数据作为验证集,且考虑到IPSO-EGM(1,1)-WT模型具有递进优化组合流程,提出以ZZJ1监测点为例,进行对比分析,以验证各递进优化组合步骤的有效性。

为便于后续描述,将各递进优化组合步骤的预测模型命名如下。预测模型1: GM(1,1)模型; 预测模型2: EGM(1,1)模型; 预测模型3: PSO-EGM(1,1)模型; 预测模型4: IPSO-EGM(1,1)模型; 预测模型5: IPSO-EGM(1,1)-WT模型。

首先,得到5类预测模型的预测结果如表3所示。

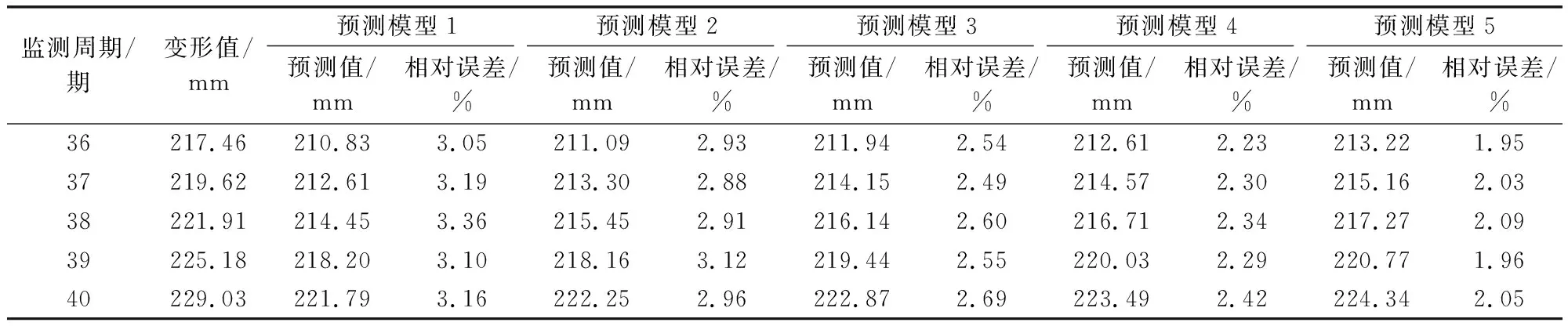
表3 预测模型1—5的预测结果统计Tab.3 Prediction results of prediction model 1—5

据表3,以各预测模型的相对误差为评价指标,统计其特征参数如下。预测模型1的相对误差平均值为3.17%,方差值为0.014 0(%)2; 预测模型2的相对误差平均值为2.96%,方差值为0.008 8(%)2; 预测模型3的相对误差平均值为2.57%,方差值为0.005 7(%)2; 预测模型4的相对误差平均值为2.32%,方差值为0.004 9(%)2; 预测模型5的相对误差平均值为2.02%,方差值为0.003 6(%)2。

由此可知,从预测模型1至模型5,预测精度及预测结果的稳定性具逐步提高趋势,充分验证了各递进优化组合步骤的有效性。其中,预测模型1和预测模型2对比,验证了分数阶算子对灰色模型的优化能力; 预测模型3和预测模型4对比,得出IPSO算法较粒子群(partide swarm optimization,PSO)算法具有更好的优化能力; 预测模型5较其余模型的预测效果优势明显,充分验证了通过IPSO-EGM(1,1)-WT模型开展滑坡变形预测的合理性。

其次,再以IPSO-EGM(1,1)-WT模型开展其余监测点的预测分析,结果如表4所示。

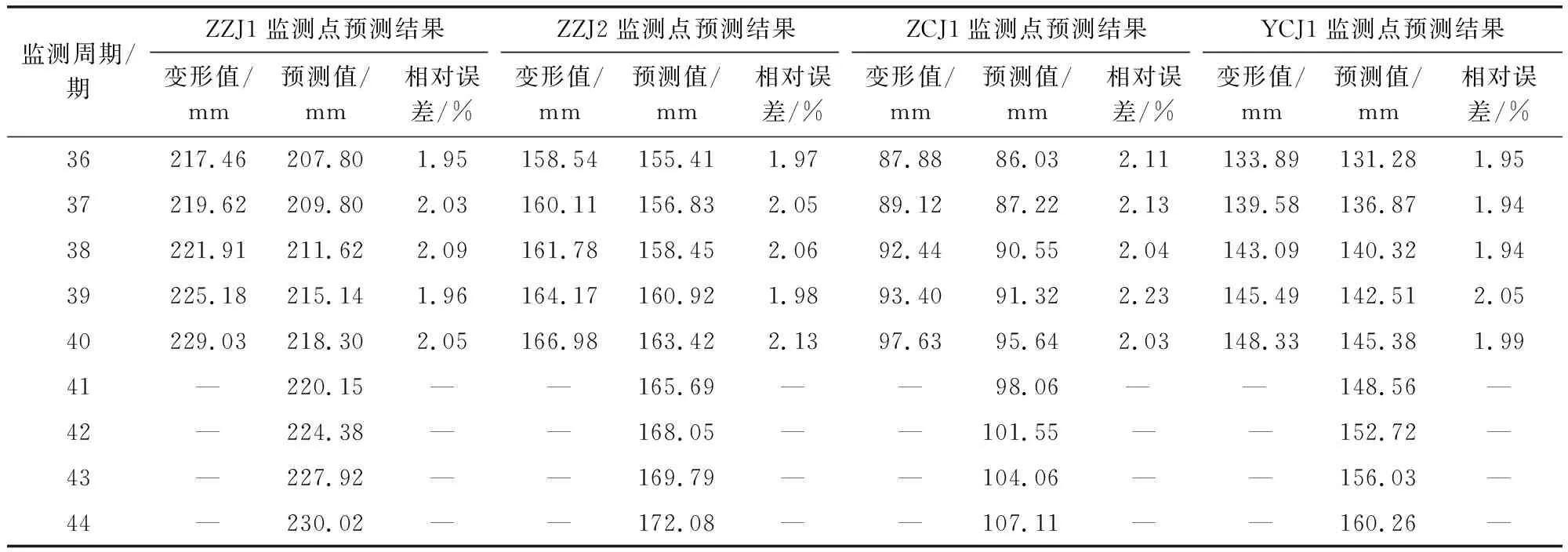
表4 各监测点的最终预测结果Tab.4 Final prediction results for each monitoring point

据表4,各监测点的预测结果存在一定差异,其预测结果的特征参数为如下。ZZJ1监测点的相对误差平均值为2.02%,方差值为0.003 6(%)2; ZZJ2监测点的相对误差平均值为2.04%,方差值为0.004 3(%)2; ZCJ1监测点的相对误差平均值为2.11%,方差值为0.006 5(%)2; YCJ1监测点的相对误差平均值为1.97%,方差值为0.002 2(%)2。

据上,各监测点的相对误差均值多在2%左右,方差值也较小,充分验证了IPSO-EGM(1,1)-WT模型的预测能力及稳定性。

最后,再统计得到各监测点的V1速率和V2速率如图4所示。

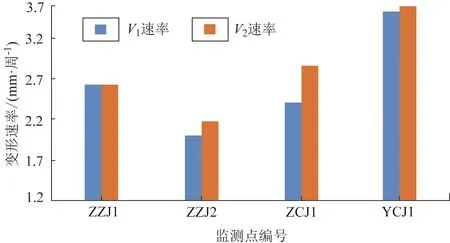
图4 滑坡变形速率的对比Fig.4 Comparison of landslide deformation rate

据图4,各监测点的V2速率均不同程度地略大于V1速率,因此,说明滑坡各位置处的后续变形速率还会进一步增加,滑坡累计变形具加速增加趋势,即滑坡稳定性在现有基础上,还会进一步减弱。

综合2.2.1节滑坡稳定性现状评价结果和 2.2.2 节滑坡稳定性预测评价结果,得出本文实例滑坡现有稳定性已较弱,剩余安全储备已较少,且后续变形仍会加速,不利于滑坡稳定,即其后续稳定性仍会进一步减弱,需尽快开展此滑坡防治研究。

3 结论

(1)浅层滑坡的影响因素主要包括土层厚度因素、地形条件因素、地层岩性因素、地质构造因素、植被与土地利用因素、降雨因素及人类工程活动因素,尤其是在地形、坡体结构等因素存在的基础上,受降雨、人类工程活动长期诱发产生的。

(2)在滑坡稳定性现状评价结果中: 天然工况条件下,稳定性系数为1.21,属稳定状态; 暴雨工况条件下,稳定性系数为1.02,属欠稳定状态; 地震工况条件下,稳定性系数为1.09,属基本稳定状态。说明不利工况条件下具潜在失稳风险。在后续预测过程中,IPSO-EGM(1,1)-WT模型能有效实现浅层滑坡的高精度预测,且预测结果显示,滑坡各位置处的后续变形速率还会进一步增加,且滑坡累计变形具加速增加趋势,说明在本次监测时段后的滑坡稳定性将趋于减弱。