一种基于遗传算法的无人潜水器推力分配优化方法
徐 蕾,宋俊辉,涂绍平,朱 俊,李仁雄
(上海中车艾森迪海洋装备有限公司,上海 201306)
0 引言
遥控无人潜水器(remotely operated vehicle,ROV)是水下作业的重要工具,在搜索救援、水产养殖和水下工程结构检测等多个领域广泛应用[1-2]。ROV 的推进器布置与推力分配对ROV 的运动和作业能力影响巨大。通过对ROV的推进系统进行合理的推力分配不仅可以使ROV的各推进器高效稳定地运行,并且可满足ROV期望的推力或力矩的输出要求。常见推力分配方法主要有:基于数学规划的优化方法、原始对偶法、伪逆法等[3-5]。伪逆法求解迅速、结构简单,但输出推力易饱和,使推进器持续高功率工作;原始对偶法的理论简单,有效解决了推力饱和现象,但推力大小存在突变,降低了推进器的使用寿命[3-6]。对于未来推力分配技术的发展,智能控制分配将有很大的潜力。智能控制分配收敛速度快、精度高、结果一般能达到最优,而且适合解决控制分配当中的非线性问题[6]。现在可用于推力分配的智能算法包括神经网络、粒子群优化、遗传算法等。其中,遗传算法是一种通过模拟自然进化过程搜索空间最优解的方法[7]。
针对ROV推力分配的输出饱和问题,本文提出一种基于遗传算法的无人潜水器推力分配优化方法。本文以某微小型电动ROV 的推进器空间布局为基础建立了ROV水平面与垂直面的推力数学模型,应用遗传算法分别对ROV 的水平面与垂直面的推进器的推力分配进行优化。本文所提方法不仅通过编码将优化目标-输出推力限定在一定范围内,避免推力输出饱和,并且通过选择合适的优化目标函数,在满足一定工程误差条件下,使ROV各推进器的输出合力或合力矩基本吻合期望输出的合力或合力矩。
1 ROV推进器矢量布局与数学建模
1.1 ROV推进器布局与推进器性能参数
本文所论述的ROV 本体上安装8 台相同型号的电动推进器,推进器布局如图1所示。根据国际水池会议(ITTC)推荐和造船与轮机工程学会(SNAME)术语公报的体系,建立ROV 随体坐标系。水平面上的4 台推进器(T1~T4)的安装轴线与ROV 的x轴的夹角α为45°,采用“面对面”矢量环形对称布置,其中a、b分别为水平面各推进器推力的作用点到x轴、y轴的距离。垂直面上的4 台推进器(T5~T8)的安装轴线与z轴平行,并沿xOz平面对称布置,其中c、d分别为垂直面各推进器推力的作用点到x轴、y轴的距离。

图1 推进器布局简图Fig.1 Layout diagram of thrusters
推进器的最大转速为1 100 r/min,正转(顺时针转)最大推力为14.18 kgf(1 kgf≈9.8 N),反转(逆时针转)最大推力为13.30 kgf。推进器的转速、推力与功率之间的测试数据如表1所示。
为方便后续的仿真计算,将表1的测试数据采用最小二乘法[8]进行拟合,可以得到推进器正转时的推力与功率的函数关系式见式(1),反转时的推力与功率的函数关系式见式(2);并分别绘制出推进器正转和反转时推力与功率的拟合与实测数据的曲线,如图2~图3所示。

图2 正转推力与功率曲线Fig.2 Thrust and power curve when rotating clockwise
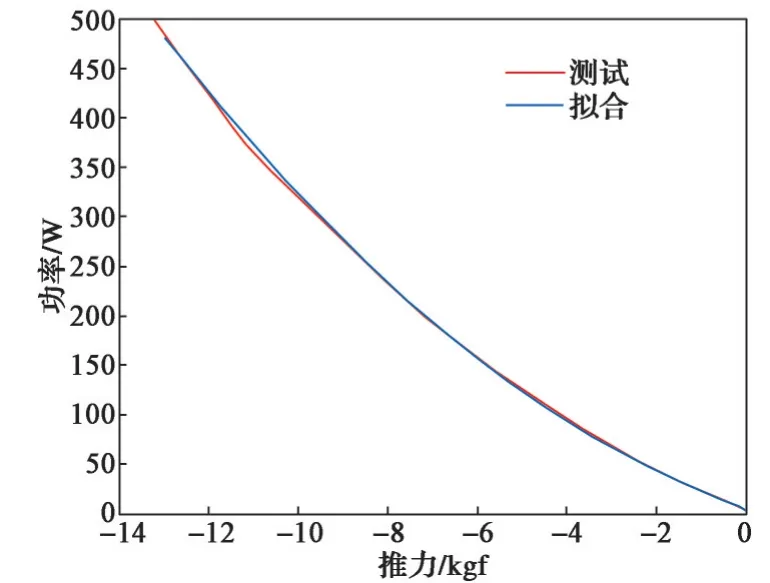
图3 反转推力与功率曲线Fig.3 Thrust and power curve when rotating counter clockwise
式中:Pcw——推进器正转时的功率;Pccw——推进器反转时的功率;τ——推力。
1.2 ROV推力数学建模
1.2.1 水平推进器数学建模
根据图1所示的ROV水平推进器的布局,将水平面内的4个推进器的推力分别沿x轴与y轴进行分解,则可以得到如图4所示的水平面各推进器的推力分解简图。T1~T4分别为推进器T1~T4的推力。
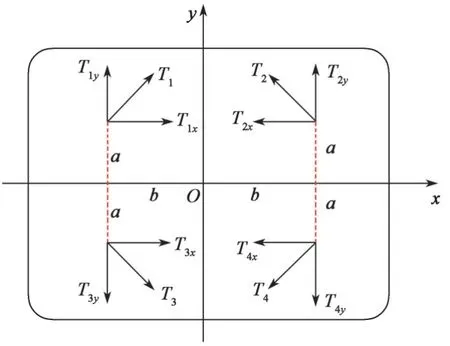
图4 水平面的推进器推力分解Fig.4 Thrust decomposition of horizontal thrusters
由图4 可以推导出沿x轴的纵向力K,沿y轴的横向力M以及绕z轴旋转的艏向偏航力矩N。
式中:L=acosα+bsinα。
由式(3)~式(5),可以进一步建立ROV 水平面推力的数学模型:
式中:fh——水平面推力函数。
1.2.2 垂直推进器数学建模
同理,根据图1 所示的ROV 垂直推进器的布局,可以推导出ROV沿z轴的沉降力P、绕x轴旋转的俯仰力矩Q以及绕y轴旋转的横滚力矩R,并建立ROV 垂直面推力的数学模型:
式中:fv——垂直面推力函数。
2 基于遗传算法优化的推力分配
2.1 遗传算法简介
遗传算法[9-10]( genetic algorithm,GA)是1962 年由美国的 Holland 提出的一种模仿生物进化过程的最优化方法,是一种通过模拟自然进化过程搜索空间最优解的方法[7]。遗传算法将要优化的问题模拟成一个“优胜劣汰”的生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度低的函数值的解,增加适应度高的函数值的解, 使群体一代代不断进化,最后搜索到问题的最优解。遗传算法的运算过程如图5 所示。其中,n表示种群的代数。

图5 遗传算法流程Fig.5 GA flowchart
2.2 遗传算法的操作
遗传算法是一个迭代过程,其模拟生物在自然环境的遗传与进化机理,反复进行选择操作、交叉操作、变异操作,最终得到问题的最优解或者近似最优解。
2.2.1 选择操作
选择操作有多种方法,本文采用二元“锦标赛选择”法,即每次从种群中随机抽取2 个个体(是有放回的抽取),然后从抽样的2 个个体中选择适应度值最好的个体进入下一代。这样就保证了相对最优个体能够保存在种群中,提高了搜索到最优解的速度。
2.2.2 交叉操作
在遗传算法中常采用单点交叉法。单点交叉法的过程:首先,在种群中根据一定的交叉率pc随机选择一定数量的个体作为父本;然后,随机设置一个交叉点,交换父代双亲交叉点左侧编码串,产生新的子代个体;最后,用子代个体代替父代个体,产生新的种群。单点交叉操作过程如图6所示。

图6 单点交叉操作过程Fig.6 Process diagram of single point cross
2.2.3 变异操作
变异操作就是以变异概率改变种群中个体串码的某一个或多个点位的基因。本文采用单点变异操作。其过程如图7所示。
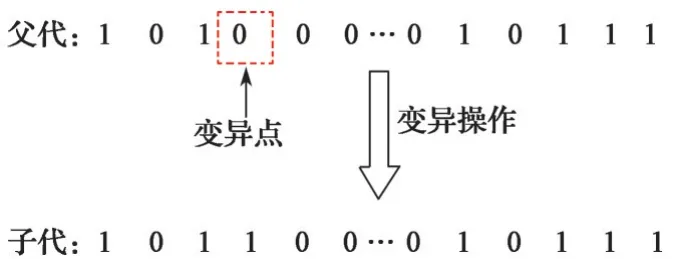
图7 单点变异操作过程Fig.7 Process diagram of single point mutation
2.3 推力分配的优化目标与适应度函数的选取
2.3.1 优化目标函数的选取
应用遗传算法优化ROV 推力分配的实质就是选择合适的目标函数对各推进器的输出力进行优化,使各推进器的输出在推进器的有效推力范围内,并且使各推进器的输出合力(矩)与期望的合力(矩)相等或满足一定误差。本文将期望的合力或力矩与各推进器的输出合力或力矩的差值的绝对值,作为优化推力分配的目标函数的组成项。
定义ROV水平面推进器的期望输出合力矩阵Fh:
式中:Ks——期望输出的纵向合力;Ms——期望输出的横向合力;Ns——期望输出的艏向偏航合力矩。
定义ROV 垂直面各推进器的期望输出合力矩阵Fv:
式中:Ps——期望输出的沉降合力;Qs——期望输出的横滚合力矩;Rs——期望输出的俯仰合力矩。
另外,考虑推进器推力输出的平稳性,将推进器输出推力的变化作为优化目标的一项。因此,将推进器本时刻与上一时刻的输出推力的差值的绝对值作为目标的优化项。
此外,考虑推进器的功耗,将推进器的输出功率与最大功率的比值加入目标函数中。
综上,将上述三项分别乘以不同的权重作为推力分配优化的目标函数,即目标函数为
式中:w1、w2、w3——权值,w1+w2+w3=1,这里取w1=0.6,w2=0.1,w3= 0.3;pi——推进器Ti的输出功率,pi可以根据式(1)或式(2)计算得出;pmax——推进器的最大输出功率;Ti(k)——推进器Ti在k时刻的输出推力。
2.3.2 适应度函数的选取
适应度函数的选取直接影响遗传算法的收敛速度以及能否找到最优解[11]。本文选取目标函数作为适应度函数,即
3 仿真分析
为验证遗传算法对ROV 推力分配的优化效果,采用遗传算法分别对ROV 水平面和垂直面的推进器的推力分配进行优化,并与伪逆法推力分配效果进行对比。设置遗传算法的种群数为200,种群个体采用二进制编码,最大迭代次数为100,交叉率pc为0.8,变异率pm为0.05,并按照推进器推力范围[-13 kgf,14 kgf]进行编码。根据式(10)与式(11)计算出目标函数的值与个体的适应度,并按照前述遗传算法的选择、交叉、变异操作,一直迭代到遗传算法设定的最大迭代次数。
3.1 水平面推力分配仿真分析
3.1.1 基于遗传算法的水平面推力分配仿真分析
假设ROV期望输出的纵向合力Ks与横向合力Ms分别如下:
从Ks与Ms的表达式可以看出,Ks与Ms是随时间t变化的,并且从运动方向看,要求ROV 在x轴与y轴2个自由度同时运动,耦合性比较高。这对水平面各推进器的推力分配来说是有难度的。采用前述的遗传算法对水平面各推进器的推力分配进行优化,通过仿真得到水平面的期望合力(Ks、Ms)、实际输出推力的合力(Kr、Mr)、期望合力与实际输出合力的差以及水平面各推进器(T1~T4)的推力输出。仿真结果分别如图8~图10所示。

图8 Ks、Kr、Ms和Mr曲线Fig.8 Curve graph of Ks , Kr , Ms and Mr
从图8~图9 可以看出,基于遗传算法优化的水平面推进器的输出合力与期望合力基本一致,误差约在±0.1 kgf,换算成比率,误差约在±0.5%范围之内。另外,从图10 可以看出,水平面的推进器T1~T4的输出推力均在[-13 kgf,14 kgf]范围内,各推进器输出没有出现饱和现象,且在整个运动过程中各推进器推力的变化趋势比较平缓,基本没有出现大跳变。
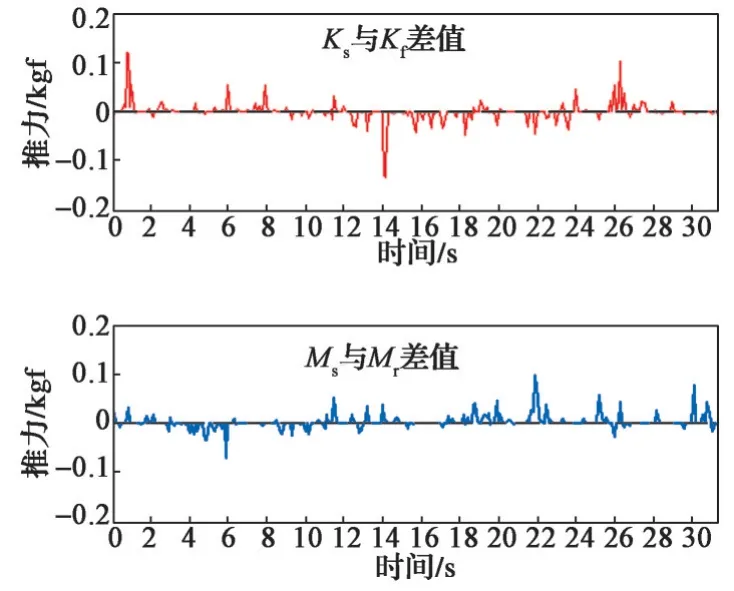
图9 Ks与Kr差值、Ms与Mr差值Fig.9 The difference between Ks and Kr , the difference between Ms and Mr

图10 基于遗传算法推进器T1~T4推力输出Fig.10 Thrust output graph of T1-T4 based on GA
3.1.2 伪逆法水平面推力分配仿真分析
将期望推力纵向合力Ks与横向合力Ms(式(12)、式(13))采用伪逆分配方法进行推力分配仿真,推力分配的结果如图11所示。

图11 基于伪逆法的推进器T1~T4 推力输出Fig.11 Thrust output of T1-T4 based on pseudo inverse method
将图11与图10对比可以看出,采用伪逆法进行推力分配时,虽然推进器T1~T4 的输出相比基于遗传算法的推力分配输出要平滑,但是推进器T3的最大输出推力达到了20 kgf,出现了饱和现象,而推进器T2 的输出基本却为零,并没有有效利用推进器T2。因此,可以明显看出,遗传算法优化的推力输出没有出现饱和现象,并且推进器T1~T4的输出更加均衡,每个推进器都得到了充分的利用。
3.2 垂直面推进器推力分配仿真分析
3.2.1 基于遗传算法的横滚与俯仰力矩分配仿真
采用遗传算法对ROV 俯仰和横滚力矩的分配进行优化。假设ROV 期望输出的横滚力矩Qs和俯仰力矩Rs分别为
仿真得到垂直面各推进器(T5~T8)的输出推力的合力矩与期望合力矩、实际输出合力矩与期望合力矩的差以及垂直面各推进器(T5~T8)的推力输出。仿真结果分别如图12~图14所示。
从图12~图13 可以看出,应用遗传算法优化的横滚力矩和俯仰力矩与其各自的期望输出基本一致,期望输出与实际输出之间的误差约在±0.2 kgf,换算成比率,误差范围在±1%之内。另外,从图14 可以看出,推进器T5~T8 的输出推力均在[-13,14]范围内,没有出现饱和现象。
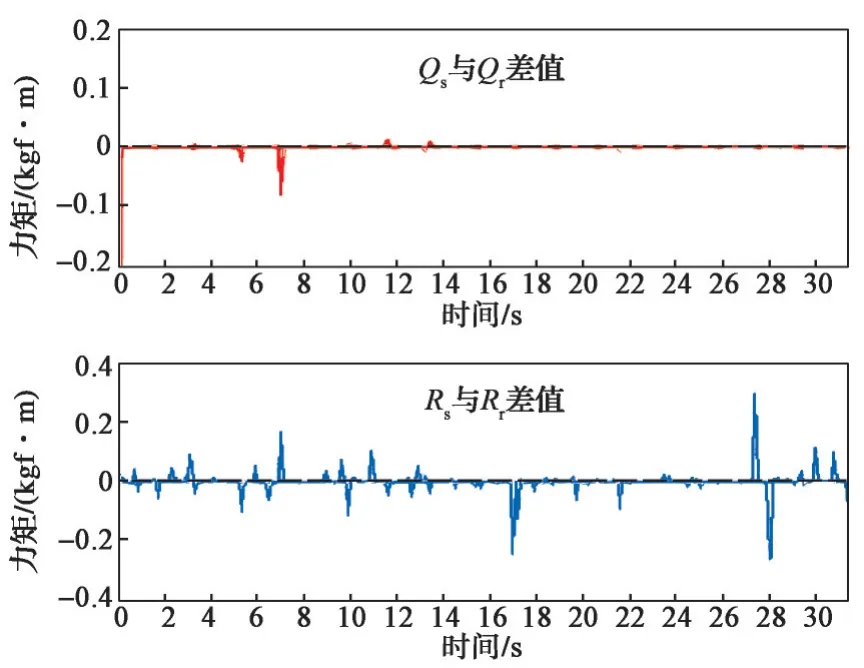
图13 Qs与Qr差值、Rs与Rr差值Fig.13 The difference between Qs and Qr , the difference between Rs and Rr

图14 基于遗传算法的推进器T5~T8 推力输出Fig.14 Thrust output graph of T5-T8 based on GA
3.2.2 伪逆法的横滚与俯仰力矩分配仿真
将期望的横滚力矩Qs和俯仰力矩Rs(式(14)、式(15))采用伪逆分配方法进行推力分配仿真,推力分配的结果如图15 所示。
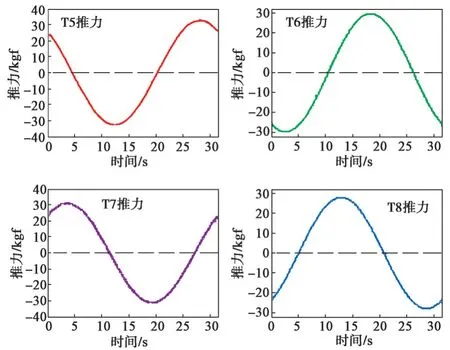
图15 基于伪逆法的推进器T5~T8 推力输出Fig.15 Thrust output graph of T5-T8 based on pseudo inverse method
将图15与图14对比可以看出,采用伪逆法对横滚与俯仰力矩进行推力分配时,推进器T5~T8 的输出相比基于遗传算法的推力分配输出要平滑,但推进器T5~T8 的最大推力超过30 kgf,均超出了推进器的有效输出范围[-13,14],即均出现了饱和现象。这也意味着如果采用伪逆法进行推力分配将无法达到期望的横滚力矩和俯仰力矩输出。
4 结束语
基于现有ROV 的推进器空间布局以及推进器的测试数据,对ROV水平面与垂直面的推进器的推力进行数学建模,然后选择合适的优化目标函数,应用遗传算法分别对ROV 的水平面与垂直面的期望合力(矩)的分配优化进行仿真分析。并且,将基于遗传算法优化的推力分配仿真结果与常规的伪逆法推力分配的仿真结果进行了对比,得出以下结论:
1) 采用常规的伪逆法进行推力分配时,相比于基于遗传算法的推力分配,推进器的输出更平滑,但推进器的输出容易出现饱和现象,甚至各推进器的输出不均衡;
2) 基于遗传算法的推力分配误差小,误差可以保证在±1%以内,并且能够有效解决推力分配的饱和问题,能够均衡地利用各推进器的输出能力。
以上结论以及本文所做的探究均是在仿真基础上得出的,与实际工程应用还存在差距。后续需要搭建具体的实验平台做进一步探究,并着重解决基于遗传算法的推力分配优化的实时性以及快速性问题,减小优化的运算量,使遗传算法能够真正应用于推力分配优化的实际工程中。

